高一数学人教A版必修1课件:3.1.2 用二分法求方程的近似解 课件(共22张PPT)
文档属性
| 名称 | 高一数学人教A版必修1课件:3.1.2 用二分法求方程的近似解 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-16 22:35:29 | ||
图片预览








文档简介
3.1.2 用二分法求方程的近似解
1、函数的零点:
对于函数 y=f (x) ,使 f (x)=0 的 实数x 叫做
函数y=f (x)的零点
2、零点存在性定理
二、基础练习
1、已知函数f(x)=x2+mx+n,若f(a)>0,f(b)>0,则
函数f(x)在区间(a,b)内( )
A.一定有零点 B.一定没有零点
C.可能有两个零点 D.至多有一个零点
C
C
B
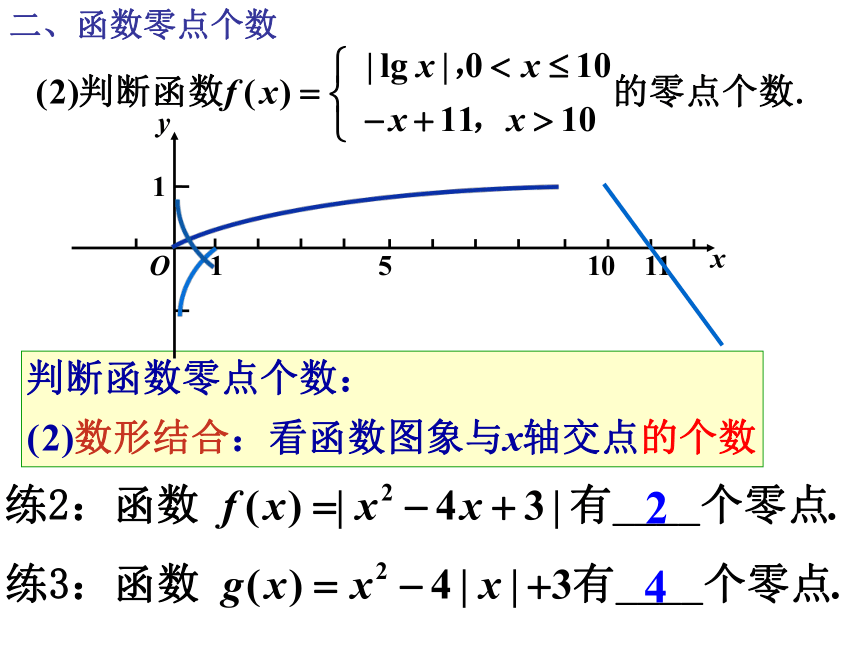
二、函数零点个数
二、函数零点个数
x
y
O
1
1
5 10 11
二、函数零点个数
二、函数零点个数
x
y
O
二、函数零点个数
D
二、函数零点个数
D
x
1
2
3
4
5
6
7
8
9
f(x)
-4
-1.306
1.098
3.386
5.609
7.791
9.945
12.079
14.197
如何求函数近似零点
问题:现有12个小球,体积均匀外表一致,但是其中有一个小球却比别的球重。如果给你一天平,最少要称几次才可以找出这个比较重的球?
解:
第一次,两端各放6个小球,低的那一端一定有重球;
第二次,两端各放3个小球,低的那一端一定有重球;
第三次,两端各放1个小球,如果平衡,剩下的就是重球;如果不平衡,则低的那一端就是重球。
一、基础知识讲解
那么零点是在(2,2.5)内,还是在(2.5,3)内?
∵ f(2.5) × f(3)<0,∴ f(x)在(2.5,3)内有零点
那么零点是在(2.5,2.75)内,还是在(2.75,3)内?
∵ f(2.5) × f(2.75)<0,∴ f(x)在(2.5,2.75)内有零点
区间(2,3)的中点是
x=2.5
区间(2.5,3)的中点是
x=2.75
… … … … …
通过缩小零点所在的范围,那么在一定的精确度的要求下,能得到零点的近似值。一般的,我们通过“取中点”的方法逐步缩小零点所在的范围。
1、二分法的概念
对于在区间[a,b]上连续不断、且f(a)?f(b)<0的函数y=f(x),通过不断把函数y=f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
一、基础知识讲解
1、二分法的概念
对于在区间[a,b]上连续不断、且f(a)?f(b)<0的函数y=f(x),通过不断把函数y=f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
思考:是不是所有的函数都可用二分法求零点?
一、基础知识讲解
1、二分法的概念
对于在区间[a,b]上连续不断、且f(a)?f(b)<0的函数y=f(x),通过不断把函数y=f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
区间(a,b)
中点的值
中点函数值符号
区间长度
(2,3)
2.5
﹣
2.75
2.625
﹢
﹢
2.5625
﹢
(2.5,3)
(2.5,2.75)
(2.5,2.625)
(2.5,2.5625)
2.53125
﹣
由于 |2.5-2.5625|=0.0625<0.1
所以原函数精确度为0.1的零点近似解为2.5(或2.5625)。
1
0.5
0.25
0.125
0.0625
⑴确定原始区间[a,b],验证 f(a)?f(b)<0,给定精确度 ε
⑵求区间(a,b)的中点c
⑶计算f(c);
①若f(c)=0,则c就是 函数的零点
②若f(a)? f(c)<0,则令b= c (此时零点x0∈(a,c))
③若f(b)? f(c) <0,则令a= c (此时零点x0∈(c,b))
⑷判断是否达到精确度 ε,即若|a-b|< ε,则得到零点的近似值 a(或b);否则得重复⑵ ~ ⑷
2、二分法的基本步骤
例2、已知方程 2x+3x=7 的解在区间(1,2)内
利用二分法求该方程的近似解(精确度0.1)
区间
中点的值
中点函数近似值
区间长度
(1,2)
1.5
0.33
1.25
1.375
-0.28
-0.87
1.4375
0.02
(1,1.5)
(1.25,1.5)
(1.375,1.5)
(1.375,1.4375)
由于 |1.375-1.4375|=0.0625<0.1
所以原方程近似解可取1.375(或1.4375)。
1
0.25
0.5
0.125
0.0625
练习:
练习:
2、对于在区间[a,b]上连续不断、且f(a)?f(b)<0的函数y=f(x),通过不断把函数y=f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
⑴确定区间[a,b],验证 f(a)?f(b)<0,给定精确度 ε
⑵求区间(a,b)的中点c
⑶计算f(c);
①若f(c)=0,则c就是 函数的零点
②若f(a)? f(c)<0,则令b= c (此时零点x0∈(a,c))
③若f(a)? f(c)>0,则令a= c (此时零点x0∈(c,b))
⑷判断是否达到精确度 ε,即若|a-b|< ε,则得到零点的近似值 a(或b);否则得重复⑵ ~ ⑷
3、二分法的基本步骤
《练习册》:P88选择题
P59 1-4
P57 例1
作业
1、函数的零点:
对于函数 y=f (x) ,使 f (x)=0 的 实数x 叫做
函数y=f (x)的零点
2、零点存在性定理
二、基础练习
1、已知函数f(x)=x2+mx+n,若f(a)>0,f(b)>0,则
函数f(x)在区间(a,b)内( )
A.一定有零点 B.一定没有零点
C.可能有两个零点 D.至多有一个零点
C
C
B
二、函数零点个数
二、函数零点个数
x
y
O
1
1
5 10 11
二、函数零点个数
二、函数零点个数
x
y
O
二、函数零点个数
D
二、函数零点个数
D
x
1
2
3
4
5
6
7
8
9
f(x)
-4
-1.306
1.098
3.386
5.609
7.791
9.945
12.079
14.197
如何求函数近似零点
问题:现有12个小球,体积均匀外表一致,但是其中有一个小球却比别的球重。如果给你一天平,最少要称几次才可以找出这个比较重的球?
解:
第一次,两端各放6个小球,低的那一端一定有重球;
第二次,两端各放3个小球,低的那一端一定有重球;
第三次,两端各放1个小球,如果平衡,剩下的就是重球;如果不平衡,则低的那一端就是重球。
一、基础知识讲解
那么零点是在(2,2.5)内,还是在(2.5,3)内?
∵ f(2.5) × f(3)<0,∴ f(x)在(2.5,3)内有零点
那么零点是在(2.5,2.75)内,还是在(2.75,3)内?
∵ f(2.5) × f(2.75)<0,∴ f(x)在(2.5,2.75)内有零点
区间(2,3)的中点是
x=2.5
区间(2.5,3)的中点是
x=2.75
… … … … …
通过缩小零点所在的范围,那么在一定的精确度的要求下,能得到零点的近似值。一般的,我们通过“取中点”的方法逐步缩小零点所在的范围。
1、二分法的概念
对于在区间[a,b]上连续不断、且f(a)?f(b)<0的函数y=f(x),通过不断把函数y=f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
一、基础知识讲解
1、二分法的概念
对于在区间[a,b]上连续不断、且f(a)?f(b)<0的函数y=f(x),通过不断把函数y=f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
思考:是不是所有的函数都可用二分法求零点?
一、基础知识讲解
1、二分法的概念
对于在区间[a,b]上连续不断、且f(a)?f(b)<0的函数y=f(x),通过不断把函数y=f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
区间(a,b)
中点的值
中点函数值符号
区间长度
(2,3)
2.5
﹣
2.75
2.625
﹢
﹢
2.5625
﹢
(2.5,3)
(2.5,2.75)
(2.5,2.625)
(2.5,2.5625)
2.53125
﹣
由于 |2.5-2.5625|=0.0625<0.1
所以原函数精确度为0.1的零点近似解为2.5(或2.5625)。
1
0.5
0.25
0.125
0.0625
⑴确定原始区间[a,b],验证 f(a)?f(b)<0,给定精确度 ε
⑵求区间(a,b)的中点c
⑶计算f(c);
①若f(c)=0,则c就是 函数的零点
②若f(a)? f(c)<0,则令b= c (此时零点x0∈(a,c))
③若f(b)? f(c) <0,则令a= c (此时零点x0∈(c,b))
⑷判断是否达到精确度 ε,即若|a-b|< ε,则得到零点的近似值 a(或b);否则得重复⑵ ~ ⑷
2、二分法的基本步骤
例2、已知方程 2x+3x=7 的解在区间(1,2)内
利用二分法求该方程的近似解(精确度0.1)
区间
中点的值
中点函数近似值
区间长度
(1,2)
1.5
0.33
1.25
1.375
-0.28
-0.87
1.4375
0.02
(1,1.5)
(1.25,1.5)
(1.375,1.5)
(1.375,1.4375)
由于 |1.375-1.4375|=0.0625<0.1
所以原方程近似解可取1.375(或1.4375)。
1
0.25
0.5
0.125
0.0625
练习:
练习:
2、对于在区间[a,b]上连续不断、且f(a)?f(b)<0的函数y=f(x),通过不断把函数y=f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
⑴确定区间[a,b],验证 f(a)?f(b)<0,给定精确度 ε
⑵求区间(a,b)的中点c
⑶计算f(c);
①若f(c)=0,则c就是 函数的零点
②若f(a)? f(c)<0,则令b= c (此时零点x0∈(a,c))
③若f(a)? f(c)>0,则令a= c (此时零点x0∈(c,b))
⑷判断是否达到精确度 ε,即若|a-b|< ε,则得到零点的近似值 a(或b);否则得重复⑵ ~ ⑷
3、二分法的基本步骤
《练习册》:P88选择题
P59 1-4
P57 例1
作业
