高中物理人教版(2019)必修第二册同步练习第五章 专题精练 平抛运动规律的应用
文档属性
| 名称 | 高中物理人教版(2019)必修第二册同步练习第五章 专题精练 平抛运动规律的应用 |  | |
| 格式 | zip | ||
| 文件大小 | 706.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-14 16:25:22 | ||
图片预览



文档简介
专题精练
平抛运动规律的应用
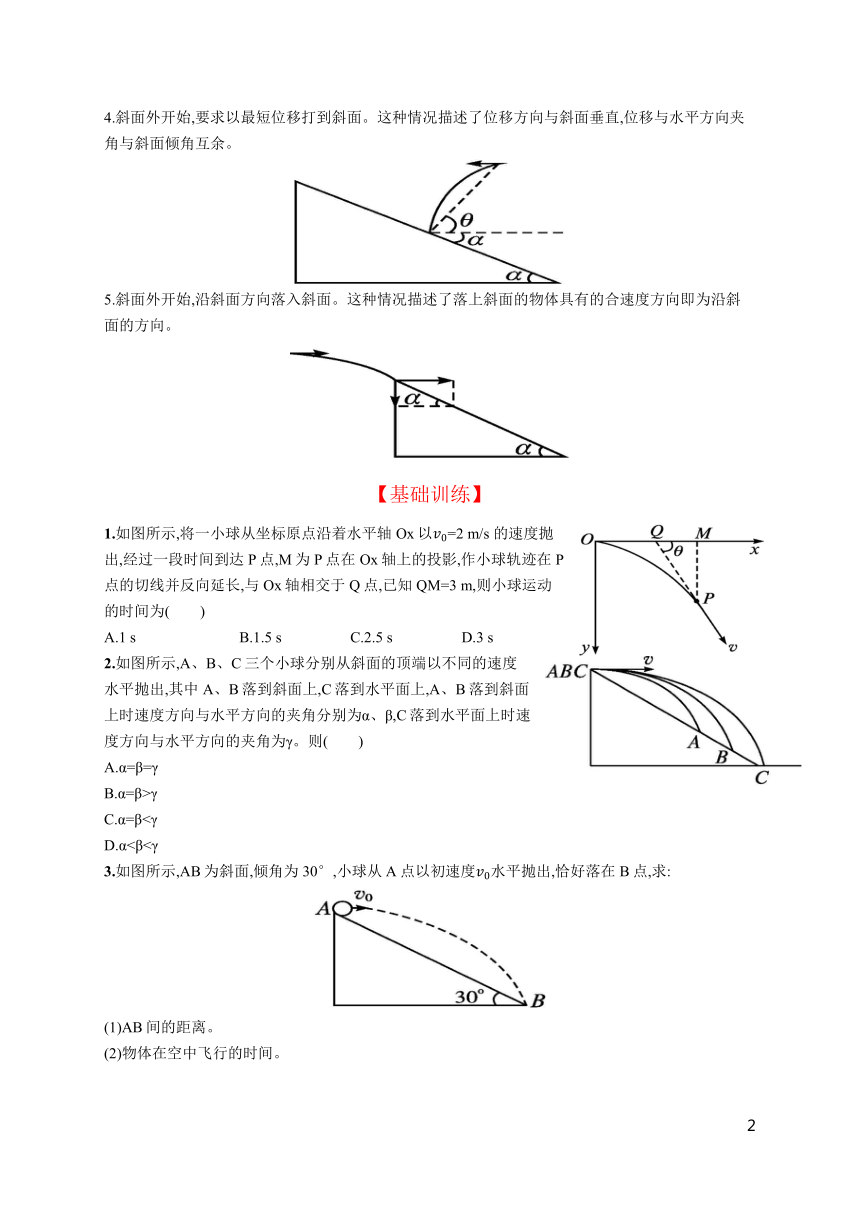
【知识归纳】
平抛运动的两个推论
(1)某时刻速度、位移与初速度方向的夹角θ、α的关系为tan
θ=2tan
α。
证明:如图所示,tan
θ=,tan
α=tan
θ。
(2)平抛运动的物体在任意时刻瞬时速度的反向延长线一定通过此时水平位移的中点。
证明:把速度反向延长后与x轴相交于B点,由tan
α=tan
θ,可知B为此时水平位移的中点。
平抛运动与斜面相结合
常见的几种情况是:
1.斜面顶端开始,仍落到斜面。这种情形说明位移沿斜面,即斜面的倾角就是位移与水平方向的夹角。
2.斜面外开始,垂直打在斜面上。这种情形描述了速度的方向,即速度偏转角与斜面倾角互余。
3.斜面顶端开始,仍落到斜面,过程中何时距斜面最远。即合速度与斜面平行(速度偏向角等于斜面倾角)的点。原因是在此之前和之后合速度都有垂直斜面的分速度。
4.斜面外开始,要求以最短位移打到斜面。这种情况描述了位移方向与斜面垂直,位移与水平方向夹角与斜面倾角互余。
5.斜面外开始,沿斜面方向落入斜面。这种情况描述了落上斜面的物体具有的合速度方向即为沿斜面的方向。
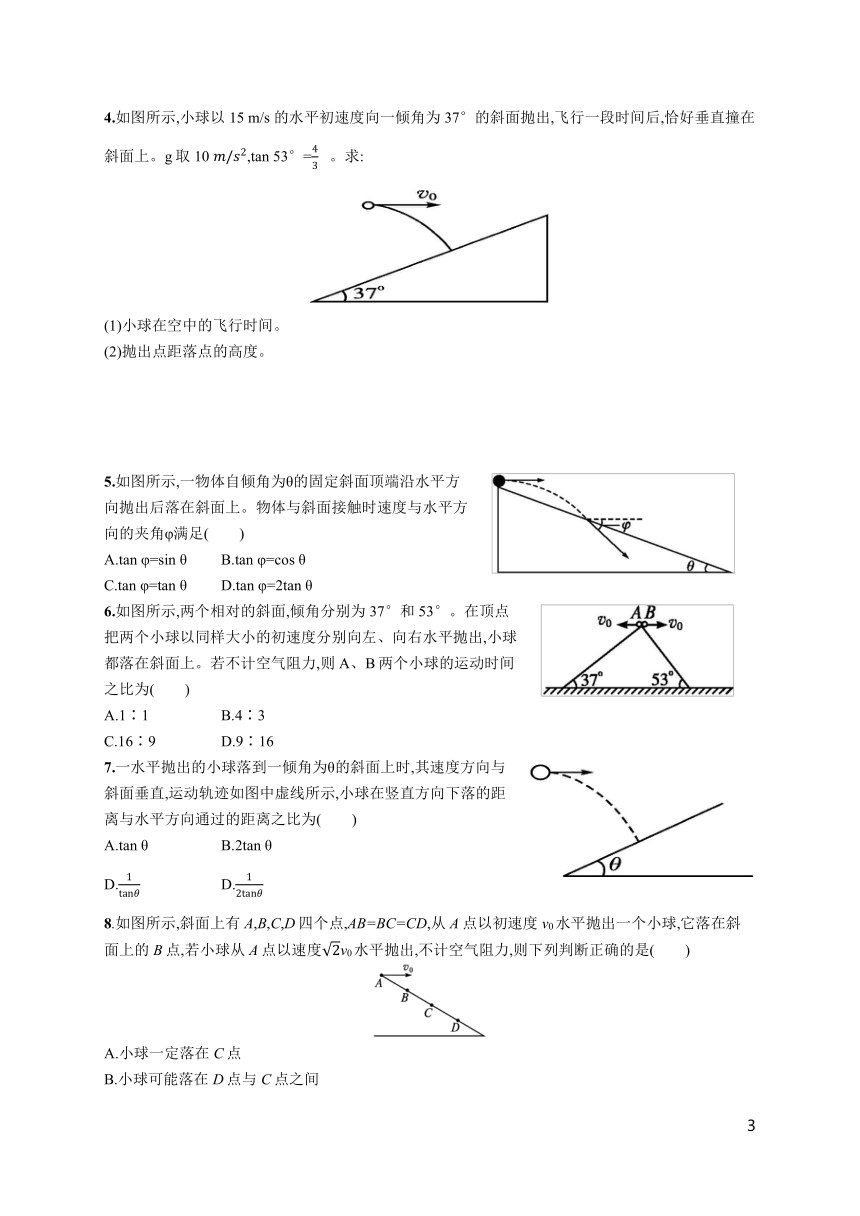
【基础训练】
1.如图所示,将一小球从坐标原点沿着水平轴Ox以=2
m/s
的速度抛出,经过一段时间到达P点,M为P点在Ox轴上的投影,作小球轨迹在P点的切线并反向延长,与Ox轴相交于Q点,已知QM=3
m,则小球运动的时间为( )
A.1
s
B.1.5
s
C.2.5
s
D.3
s
2.如图所示,A、B、C三个小球分别从斜面的顶端以不同的速度水平抛出,其中A、B落到斜面上,C落到水平面上,A、B落到斜面上时速度方向与水平方向的夹角分别为α、β,C落到水平面上时速度方向与水平方向的夹角为γ。则( )
A.α=β=γ
B.α=β>γ
C.α=β<γ
D.α<β<γ
3.如图所示,AB为斜面,倾角为30°,小球从A点以初速度水平抛出,恰好落在B点,求:
(1)AB间的距离。
(2)物体在空中飞行的时间。
4.如图所示,小球以15
m/s
的水平初速度向一倾角为37°的斜面抛出,飞行一段时间后,恰好垂直撞在斜面上。g取10
,tan
53°=
。求:
(1)小球在空中的飞行时间。
(2)抛出点距落点的高度。
5.如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上。物体与斜面接触时速度与水平方向的夹角φ满足( )
A.tan
φ=sin
θ
B.tan
φ=cos
θ
C.tan
φ=tan
θ
D.tan
φ=2tan
θ
6.如图所示,两个相对的斜面,倾角分别为37°和53°。在顶点把两个小球以同样大小的初速度分别向左、向右水平抛出,小球都落在斜面上。若不计空气阻力,则A、B两个小球的运动时间之比为( )
A.1∶1
B.4∶3
C.16∶9
D.9∶16
7.一水平抛出的小球落到一倾角为θ的斜面上时,其速度方向与斜面垂直,运动轨迹如图中虚线所示,小球在竖直方向下落的距离与水平方向通过的距离之比为( )
A.tan
θ
B.2tan
θ
D.
D.
8.如图所示,斜面上有A,B,C,D四个点,AB=BC=CD,从A点以初速度v0水平抛出一个小球,它落在斜面上的B点,若小球从A点以速度v0水平抛出,不计空气阻力,则下列判断正确的是( )
A.小球一定落在C点
B.小球可能落在D点与C点之间
C.小球落在斜面的运动方向与斜面的夹角一定增大
D.小球落在斜面的运动方向与斜面的夹角不相同
9.(多选)跳台滑雪是一种勇敢者的滑雪运动,运动员穿专用滑雪板,在滑雪道上获得一定速度后从跳台飞出,在空中飞行一段距离后着陆。现有某运动员先后两次从跳台a处沿水平方向飞出,初速度分别为v和2v,两次均在斜坡上着陆。不计空气阻力,下列判断正确的是( )
A.运动员两次在空中飞行的时间之比是1∶2
B.运动员两次在空中飞行的位移之比是1∶2
C.运动员两次落在斜坡上的瞬时速度大小之比是1∶2
D.运动员两次落在斜坡上的瞬时速度与水平方向夹角的正切值之比是1∶2
10.如图所示,某物体以水平初速度抛出,飞行
s后,垂直地撞在倾角θ为30°的斜面上(g取10
m/s2),由此计算出物体的水平位移x和水平初速度v0分别是( )
A.x=25
m
B.x=5
m
C.v0=10
m/s
D.v0=20
m/s
【提高训练】
1.如图所示,从同一水平线上的不同位置,沿水平方向抛出两小球A、B,不计空气阻力。要使两小球在空中相遇,则必须( )
A.先抛出A球
B.先抛出B球
C.同时抛出两球
D.两球质量相等
2.在一斜面顶端,将甲、乙两个小球分别以v和的速度沿同一方向水平抛出,两球都落在该斜面上。甲球落至斜面时的速率是乙球落至斜面时速率的( )
A.2倍
B.4倍
C.6倍
D.8倍
3.如图所示,一光滑斜面与竖直方向成α角,一小球有两种方式释放:第一种方式在A点以初速度v0平抛落至B点;第二种方式是在A点松手后沿斜面自由下滑。求:
(1)两种方式到B点,平抛的运动时间为t1,下滑的时间为t2,则等于多少?
(2)两种方式到B点的竖直分速度是多少?
4.(多选)如图所示为湖边一倾角为30°的大坝横截面示意图,水面与大坝的交点为O。一人站在A点以速度v0沿水平方向扔一个小石子,已知AO=40
m,不计空气阻力,不考虑小石子反弹过程,g取10
m/s2。下列说法正确的有
( )
A.若v0=10
m/s,则石子刚好落在水面与大坝的交点
B.若v0=5
m/s,则石子落在AO的中点
C.若小石子能直接落入水中,则v0越大,在空中飞行的时间就越长
D.若小石子不能直接落入水中,则v0越大,在空中飞行的时间就越长
5.(多选)如图,在半径为R的圆环圆心O正上方的P点,将一小球以速度v0水平抛出后恰能从圆环上Q点沿切线飞过,若OQ与OP间夹角为θ,不计空气阻力。则( )
A.从P点运动到Q点的时间为t=
B.从P点运动到Q点的时间为t=
C.小球运动到Q点时的速度为vQ=
D.小球运动到Q点时的速度为vQ=
6.(多选)甲、乙两球位于同一竖直直线上的不同位置,甲比乙的位置高,如图所示,将甲、乙两球分别以v1、v2的初速度沿同一水平方向抛出,不计空气阻力,下列条件中有可能使乙球击中甲球的是( )
A.同时抛出
B.甲早抛出
C.初速度v1>v2
D.初速度v17.(多选)如图(a),在跳台滑雪比赛中,运动员在空中滑翔时身体的姿态会影响其下落的速度和滑翔的距离。某运动员先后两次从同一跳台起跳,每次都从离开跳台开始计时,用v表示他在竖直方向的速度,其v-t图像如图(b)所示,t1和t2是他落在倾斜雪道上的时刻。则( )
图(a)
图(b)
A.第二次滑翔过程中在竖直方向上的位移比第一次的小
B.第二次滑翔过程中在水平方向上的位移比第一次的大
C.第二次滑翔过程中在竖直方向上的平均加速度比第一次的大
D.竖直方向速度大小为v1时,第二次滑翔在竖直方向上所受阻力比第一次的大
8.如图所示,a为竖直平面内的半圆环acb的水平直径,c为环上最低点,环半径为R。将一个小球从a点以初速度沿ab方向抛出,设重力加速度为g,不计空气阻力。
A.当小球的初速度时,掉到环上时的竖直分速度最大
B.当小球的初速度时,将撞击到环上的圆弧ac段
C.当取适当值,小球可以垂直撞击圆环
D.无论取何值,小球都不可能垂直撞击圆环
9.如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为.小球B从同一点Q处自由下落,下落至P点的时间为.不计空气阻力,则=( )
A.1∶2
B.1∶
C.1∶3
D.1∶
10.跳台滑雪是2022年北京冬奥会的重要比赛项目之一。比赛中运动员穿着专用滑雪板,在滑雪道上获得一定速度后从跳台飞出,在雪中飞行一段距离后着陆。现有某运动员从跳台a处沿水平方向飞出,在斜坡b处着陆,如图所示a、b间的距离为L=40
m,斜坡与水平方向的夹角为θ=30°,不计空气阻力,g取10
m/s2,运动员和滑雪板可以看成质点。求:
(1)运动员在空中飞行的时间;
(2)运动员从a点飞出的速度大小;
(3)运动员在空中何时离坡面最远,最远距离是多少?
参考答案
【基础训练】
1.
【解析】由平抛运动推论可知,Q为OM的中点,则从O点运动到P点的过程中,小球发生的水平位移x=OM=2QM=6
m。由于水平方向做匀速直线运动,则小球在这段过程中运动的时间为t=s=3s。故选项D正确。
【答案】D
2.
【解析】依据平抛运动规律,平抛运动的物体在任一时刻,速度方向与水平方向的夹角的正切值等于位移方向与水平方向的夹角的正切值的2倍,A、B的位移方向相同,则α=β;如图中虚线所示,C的位移方向与水平方向的夹角小于A、B的位移方向与水平方向的夹角,所以α=β>γ,故选项B正确。
【答案】B
3.
【解析】小球做平抛运动,在水平方向上是匀速直线运动,在竖直方向上是自由落体运动,有,y=
小球由A点抛出,落在B点,故有tan
30°=
t=,x=t=
故AB间的距离L=。
【答案】(1) (2)
4.
【解析】如图所示。由几何关系知,β=90°-37°=53°。
(1)由图得tan
β=,
得飞行时间t=tan
β=2
s。
(2)高度h==×10×22
m=20
m。
【答案】(1)2
s (2)20
m
5.
【解析】竖直速度与水平速度之比为tan
φ=,竖直位移与水平位移之比为tan
θ=,故tan
φ=2tan
θ,D正确。
【答案】D
6.【解析】求时间之比只需求出落到斜面上的竖直分速度之比即可,因为=2tan
θ,所以=2tan
θ。又根据自由落体vy=gt,所以t=∝tan
θ。从平抛到落到斜面上的时间之比。选项D正确。
【答案】D
7.
【解析】本题中平抛运动的末速度与竖直方向的夹角等于斜面倾角θ,则有:tan
θ=。则下落高度与水平射程之比为,选项D正确。
【答案】D
8.
【答案】A
9.
【解析】设运动员水平飞出时的速度为v0,则根据题意可得tan
α=,解得t=,运动员在空中运动的时间和初速度成正比,故A正确;运动员的位移=t,可知位移与时间不成正比,B错误;由落地时速度可知,初速度变为原来2倍,时间变为原来2倍即竖直分速度变为原来2倍,故合速度变为原来2倍,C正确;位移方向不变,瞬时速度方向不变,D错误。
【答案】AC
10.
【解析】物体撞在斜面上时竖直分速度=gt=10
m/s,将速度进行分解,根据平行四边形定则知,tan
30°=,解得=10
m/s=10
m/s,则水平位移=10×
m=10
m。故C正确,A、B、D错误。
【答案】C
【提高训练】
1.
【解析】相遇时,两球下落的高度相同,根据t=知,两球运动的时间相等,则两球必须同时抛出。与质量无关。故C正确,A、B、D错误。
【答案】C
2.
【解析】设斜面倾角为θ,小球从斜面上水平抛出又落到斜面上,对于任意初速度v0,竖直位移和水平位移之间的关系为tan
θ=,可得飞行时间t=,落到斜面上的速度是竖直分速度和水平分速度的合速度,有v=∝v0,所以甲、乙末速度之比就是初速度之比,选项A正确。
【答案】A
3.
【解析】设AB长为L
(1)水平方向位移为Lsin
α=v0t1
竖直方向位移为Lcos
α=
两式联立可得L=
将L值代入t1,t1=
下滑物体加速度a=gcos
α,L=,
将L、a代入t2,t2=
则=cos
α。
(2)平抛运动竖直分速度v1y=gt1=
下滑运动竖直分速度v2y=v2cos
α
由于v2=
所以v2y=
则。
【答案】(1)=cos
α (2)
4.
【解析】小石子被扔出后做平抛运动,根据:AOsin
30°=gt2,得:t=
s=2
s,则小石子不落入水中的最大速度:v0=
m/s=10
m/s,即v0=10
m/s时,小石子刚好落在水面与大坝的交点,故A正确;若:v0=5
m/s<10
m/s,则小石子会落在大坝上,所以落在大坝上时位移夹角为30°,则:tan
30°=,代入v0=5
m/s可解得t2=1
s,故落到大坝上时水平位移为:x=v0t2=5×1
m=5
m,故合位移为:x合=
m=10
m=AO,故B错误;若小石子能落入水中,平抛运动的时间由高度决定,与初速度无关,故C错误;若小石子不能直接落入水中,落在大坝上位移夹角不变,根据:tan
30°=,可知v0越大,运动的时间就越长,故D正确。
【答案】AD
5.
【解析】过Q点作OP的垂线,根据几何关系可知,小球在水平方向上的位移的大小为Rsin
θ,根据Rsin
θ=v0t,可得时间为t=,故A正确,B错误。根据几何关系知,Q点的速度方向与水平方向的夹角为θ,故小球运动到Q点时的速度为vQ=,故C错误,D正确。
【答案】AD
6.
【解析】由题意可知甲的抛出点高于乙的抛出点,相遇时,甲的竖直位移大于乙的竖直位移,由h=gt2,得t=,从抛出到相遇甲运动的时间长,故要相遇,甲应早抛出;两物体的水平位移相同,甲的运动时间比较长,由x=v0t知,甲的速度要小于乙的速度,v1【答案】BD
7.
【解析】本题考查v-t图像及运动的合成和分解。从v-t图像中图线与坐标轴所围面积可知第二次面积大于第一次面积,故第二次在竖直方向上的位移比第一次的大,A错误;因为位移方向不变,而第二次竖直位移大,故第二次水平位移也大,B正确;第一次竖直方向速度变化量大,经历时间短,由知,,因此C错误;在竖直方向上根据牛顿第二定律mg-Ff=ma,知加速度大的阻力小,D正确。
【答案】BD
8.【解析】小球从a点以初速度沿ab方向抛出若恰好落到最低点C点,竖直方向:,
水平方向:,联立上述两式可得,掉到环上时的竖直分速度为,当h=g时,掉到环上时的竖直分速度最大,A项正确;当小球的初速度时,将撞击到环上的圆弧ac段,B项正确;若小球可以垂直撞击圆环,则其速度的反向延长线一定通过圆心O,则圆心O为小球做平抛运动的水平位移的中点,而无论取何值,当小球落在圆环上时的水平位移都不可能为2R,故小球都不可能垂直撞击圆环,D项正确,C项错。
【答案】ABD
9.【解析】小球做平抛运动,将小球打在斜坡上的速度分解如图所示,由几何关系可得水平方向小球做匀速直线运动,则有位移①;竖直方向小球做自由落体运动,有②,③联立上述三式解得,,。小球B从同一点Q处自由下落至P点的过程中有,解得,故,D项正确。
【答案】D
10.
【解析】(1)设运动员做平抛运动落到b点所需时间为t1,则Lsin
30°=,解得t1=2
s;
(2)从a点飞出的速度大小v0==10
m/s;
(3)将运动员实际的运动看作平行斜面方向和垂直斜面方向这两个分运动的合运动
垂直斜面方向:初速度v01=v0sin
30°=5
m/s,
加速度a1=-gcos
30°=-5
m/s2
经过时间t,垂直斜面的分速度v1=v01+a1t
当v1=0,即t=1
s时,物体距离斜面最远
最远距离d=v01t+a1t2=
m。
【答案】(1)2
s (2)10
m/s (3)
m
6
平抛运动规律的应用
【知识归纳】
平抛运动的两个推论
(1)某时刻速度、位移与初速度方向的夹角θ、α的关系为tan
θ=2tan
α。
证明:如图所示,tan
θ=,tan
α=tan
θ。
(2)平抛运动的物体在任意时刻瞬时速度的反向延长线一定通过此时水平位移的中点。
证明:把速度反向延长后与x轴相交于B点,由tan
α=tan
θ,可知B为此时水平位移的中点。
平抛运动与斜面相结合
常见的几种情况是:
1.斜面顶端开始,仍落到斜面。这种情形说明位移沿斜面,即斜面的倾角就是位移与水平方向的夹角。
2.斜面外开始,垂直打在斜面上。这种情形描述了速度的方向,即速度偏转角与斜面倾角互余。
3.斜面顶端开始,仍落到斜面,过程中何时距斜面最远。即合速度与斜面平行(速度偏向角等于斜面倾角)的点。原因是在此之前和之后合速度都有垂直斜面的分速度。
4.斜面外开始,要求以最短位移打到斜面。这种情况描述了位移方向与斜面垂直,位移与水平方向夹角与斜面倾角互余。
5.斜面外开始,沿斜面方向落入斜面。这种情况描述了落上斜面的物体具有的合速度方向即为沿斜面的方向。
【基础训练】
1.如图所示,将一小球从坐标原点沿着水平轴Ox以=2
m/s
的速度抛出,经过一段时间到达P点,M为P点在Ox轴上的投影,作小球轨迹在P点的切线并反向延长,与Ox轴相交于Q点,已知QM=3
m,则小球运动的时间为( )
A.1
s
B.1.5
s
C.2.5
s
D.3
s
2.如图所示,A、B、C三个小球分别从斜面的顶端以不同的速度水平抛出,其中A、B落到斜面上,C落到水平面上,A、B落到斜面上时速度方向与水平方向的夹角分别为α、β,C落到水平面上时速度方向与水平方向的夹角为γ。则( )
A.α=β=γ
B.α=β>γ
C.α=β<γ
D.α<β<γ
3.如图所示,AB为斜面,倾角为30°,小球从A点以初速度水平抛出,恰好落在B点,求:
(1)AB间的距离。
(2)物体在空中飞行的时间。
4.如图所示,小球以15
m/s
的水平初速度向一倾角为37°的斜面抛出,飞行一段时间后,恰好垂直撞在斜面上。g取10
,tan
53°=
。求:
(1)小球在空中的飞行时间。
(2)抛出点距落点的高度。
5.如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上。物体与斜面接触时速度与水平方向的夹角φ满足( )
A.tan
φ=sin
θ
B.tan
φ=cos
θ
C.tan
φ=tan
θ
D.tan
φ=2tan
θ
6.如图所示,两个相对的斜面,倾角分别为37°和53°。在顶点把两个小球以同样大小的初速度分别向左、向右水平抛出,小球都落在斜面上。若不计空气阻力,则A、B两个小球的运动时间之比为( )
A.1∶1
B.4∶3
C.16∶9
D.9∶16
7.一水平抛出的小球落到一倾角为θ的斜面上时,其速度方向与斜面垂直,运动轨迹如图中虚线所示,小球在竖直方向下落的距离与水平方向通过的距离之比为( )
A.tan
θ
B.2tan
θ
D.
D.
8.如图所示,斜面上有A,B,C,D四个点,AB=BC=CD,从A点以初速度v0水平抛出一个小球,它落在斜面上的B点,若小球从A点以速度v0水平抛出,不计空气阻力,则下列判断正确的是( )
A.小球一定落在C点
B.小球可能落在D点与C点之间
C.小球落在斜面的运动方向与斜面的夹角一定增大
D.小球落在斜面的运动方向与斜面的夹角不相同
9.(多选)跳台滑雪是一种勇敢者的滑雪运动,运动员穿专用滑雪板,在滑雪道上获得一定速度后从跳台飞出,在空中飞行一段距离后着陆。现有某运动员先后两次从跳台a处沿水平方向飞出,初速度分别为v和2v,两次均在斜坡上着陆。不计空气阻力,下列判断正确的是( )
A.运动员两次在空中飞行的时间之比是1∶2
B.运动员两次在空中飞行的位移之比是1∶2
C.运动员两次落在斜坡上的瞬时速度大小之比是1∶2
D.运动员两次落在斜坡上的瞬时速度与水平方向夹角的正切值之比是1∶2
10.如图所示,某物体以水平初速度抛出,飞行
s后,垂直地撞在倾角θ为30°的斜面上(g取10
m/s2),由此计算出物体的水平位移x和水平初速度v0分别是( )
A.x=25
m
B.x=5
m
C.v0=10
m/s
D.v0=20
m/s
【提高训练】
1.如图所示,从同一水平线上的不同位置,沿水平方向抛出两小球A、B,不计空气阻力。要使两小球在空中相遇,则必须( )
A.先抛出A球
B.先抛出B球
C.同时抛出两球
D.两球质量相等
2.在一斜面顶端,将甲、乙两个小球分别以v和的速度沿同一方向水平抛出,两球都落在该斜面上。甲球落至斜面时的速率是乙球落至斜面时速率的( )
A.2倍
B.4倍
C.6倍
D.8倍
3.如图所示,一光滑斜面与竖直方向成α角,一小球有两种方式释放:第一种方式在A点以初速度v0平抛落至B点;第二种方式是在A点松手后沿斜面自由下滑。求:
(1)两种方式到B点,平抛的运动时间为t1,下滑的时间为t2,则等于多少?
(2)两种方式到B点的竖直分速度是多少?
4.(多选)如图所示为湖边一倾角为30°的大坝横截面示意图,水面与大坝的交点为O。一人站在A点以速度v0沿水平方向扔一个小石子,已知AO=40
m,不计空气阻力,不考虑小石子反弹过程,g取10
m/s2。下列说法正确的有
( )
A.若v0=10
m/s,则石子刚好落在水面与大坝的交点
B.若v0=5
m/s,则石子落在AO的中点
C.若小石子能直接落入水中,则v0越大,在空中飞行的时间就越长
D.若小石子不能直接落入水中,则v0越大,在空中飞行的时间就越长
5.(多选)如图,在半径为R的圆环圆心O正上方的P点,将一小球以速度v0水平抛出后恰能从圆环上Q点沿切线飞过,若OQ与OP间夹角为θ,不计空气阻力。则( )
A.从P点运动到Q点的时间为t=
B.从P点运动到Q点的时间为t=
C.小球运动到Q点时的速度为vQ=
D.小球运动到Q点时的速度为vQ=
6.(多选)甲、乙两球位于同一竖直直线上的不同位置,甲比乙的位置高,如图所示,将甲、乙两球分别以v1、v2的初速度沿同一水平方向抛出,不计空气阻力,下列条件中有可能使乙球击中甲球的是( )
A.同时抛出
B.甲早抛出
C.初速度v1>v2
D.初速度v1
图(a)
图(b)
A.第二次滑翔过程中在竖直方向上的位移比第一次的小
B.第二次滑翔过程中在水平方向上的位移比第一次的大
C.第二次滑翔过程中在竖直方向上的平均加速度比第一次的大
D.竖直方向速度大小为v1时,第二次滑翔在竖直方向上所受阻力比第一次的大
8.如图所示,a为竖直平面内的半圆环acb的水平直径,c为环上最低点,环半径为R。将一个小球从a点以初速度沿ab方向抛出,设重力加速度为g,不计空气阻力。
A.当小球的初速度时,掉到环上时的竖直分速度最大
B.当小球的初速度时,将撞击到环上的圆弧ac段
C.当取适当值,小球可以垂直撞击圆环
D.无论取何值,小球都不可能垂直撞击圆环
9.如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为.小球B从同一点Q处自由下落,下落至P点的时间为.不计空气阻力,则=( )
A.1∶2
B.1∶
C.1∶3
D.1∶
10.跳台滑雪是2022年北京冬奥会的重要比赛项目之一。比赛中运动员穿着专用滑雪板,在滑雪道上获得一定速度后从跳台飞出,在雪中飞行一段距离后着陆。现有某运动员从跳台a处沿水平方向飞出,在斜坡b处着陆,如图所示a、b间的距离为L=40
m,斜坡与水平方向的夹角为θ=30°,不计空气阻力,g取10
m/s2,运动员和滑雪板可以看成质点。求:
(1)运动员在空中飞行的时间;
(2)运动员从a点飞出的速度大小;
(3)运动员在空中何时离坡面最远,最远距离是多少?
参考答案
【基础训练】
1.
【解析】由平抛运动推论可知,Q为OM的中点,则从O点运动到P点的过程中,小球发生的水平位移x=OM=2QM=6
m。由于水平方向做匀速直线运动,则小球在这段过程中运动的时间为t=s=3s。故选项D正确。
【答案】D
2.
【解析】依据平抛运动规律,平抛运动的物体在任一时刻,速度方向与水平方向的夹角的正切值等于位移方向与水平方向的夹角的正切值的2倍,A、B的位移方向相同,则α=β;如图中虚线所示,C的位移方向与水平方向的夹角小于A、B的位移方向与水平方向的夹角,所以α=β>γ,故选项B正确。
【答案】B
3.
【解析】小球做平抛运动,在水平方向上是匀速直线运动,在竖直方向上是自由落体运动,有,y=
小球由A点抛出,落在B点,故有tan
30°=
t=,x=t=
故AB间的距离L=。
【答案】(1) (2)
4.
【解析】如图所示。由几何关系知,β=90°-37°=53°。
(1)由图得tan
β=,
得飞行时间t=tan
β=2
s。
(2)高度h==×10×22
m=20
m。
【答案】(1)2
s (2)20
m
5.
【解析】竖直速度与水平速度之比为tan
φ=,竖直位移与水平位移之比为tan
θ=,故tan
φ=2tan
θ,D正确。
【答案】D
6.【解析】求时间之比只需求出落到斜面上的竖直分速度之比即可,因为=2tan
θ,所以=2tan
θ。又根据自由落体vy=gt,所以t=∝tan
θ。从平抛到落到斜面上的时间之比。选项D正确。
【答案】D
7.
【解析】本题中平抛运动的末速度与竖直方向的夹角等于斜面倾角θ,则有:tan
θ=。则下落高度与水平射程之比为,选项D正确。
【答案】D
8.
【答案】A
9.
【解析】设运动员水平飞出时的速度为v0,则根据题意可得tan
α=,解得t=,运动员在空中运动的时间和初速度成正比,故A正确;运动员的位移=t,可知位移与时间不成正比,B错误;由落地时速度可知,初速度变为原来2倍,时间变为原来2倍即竖直分速度变为原来2倍,故合速度变为原来2倍,C正确;位移方向不变,瞬时速度方向不变,D错误。
【答案】AC
10.
【解析】物体撞在斜面上时竖直分速度=gt=10
m/s,将速度进行分解,根据平行四边形定则知,tan
30°=,解得=10
m/s=10
m/s,则水平位移=10×
m=10
m。故C正确,A、B、D错误。
【答案】C
【提高训练】
1.
【解析】相遇时,两球下落的高度相同,根据t=知,两球运动的时间相等,则两球必须同时抛出。与质量无关。故C正确,A、B、D错误。
【答案】C
2.
【解析】设斜面倾角为θ,小球从斜面上水平抛出又落到斜面上,对于任意初速度v0,竖直位移和水平位移之间的关系为tan
θ=,可得飞行时间t=,落到斜面上的速度是竖直分速度和水平分速度的合速度,有v=∝v0,所以甲、乙末速度之比就是初速度之比,选项A正确。
【答案】A
3.
【解析】设AB长为L
(1)水平方向位移为Lsin
α=v0t1
竖直方向位移为Lcos
α=
两式联立可得L=
将L值代入t1,t1=
下滑物体加速度a=gcos
α,L=,
将L、a代入t2,t2=
则=cos
α。
(2)平抛运动竖直分速度v1y=gt1=
下滑运动竖直分速度v2y=v2cos
α
由于v2=
所以v2y=
则。
【答案】(1)=cos
α (2)
4.
【解析】小石子被扔出后做平抛运动,根据:AOsin
30°=gt2,得:t=
s=2
s,则小石子不落入水中的最大速度:v0=
m/s=10
m/s,即v0=10
m/s时,小石子刚好落在水面与大坝的交点,故A正确;若:v0=5
m/s<10
m/s,则小石子会落在大坝上,所以落在大坝上时位移夹角为30°,则:tan
30°=,代入v0=5
m/s可解得t2=1
s,故落到大坝上时水平位移为:x=v0t2=5×1
m=5
m,故合位移为:x合=
m=10
m=AO,故B错误;若小石子能落入水中,平抛运动的时间由高度决定,与初速度无关,故C错误;若小石子不能直接落入水中,落在大坝上位移夹角不变,根据:tan
30°=,可知v0越大,运动的时间就越长,故D正确。
【答案】AD
5.
【解析】过Q点作OP的垂线,根据几何关系可知,小球在水平方向上的位移的大小为Rsin
θ,根据Rsin
θ=v0t,可得时间为t=,故A正确,B错误。根据几何关系知,Q点的速度方向与水平方向的夹角为θ,故小球运动到Q点时的速度为vQ=,故C错误,D正确。
【答案】AD
6.
【解析】由题意可知甲的抛出点高于乙的抛出点,相遇时,甲的竖直位移大于乙的竖直位移,由h=gt2,得t=,从抛出到相遇甲运动的时间长,故要相遇,甲应早抛出;两物体的水平位移相同,甲的运动时间比较长,由x=v0t知,甲的速度要小于乙的速度,v1
7.
【解析】本题考查v-t图像及运动的合成和分解。从v-t图像中图线与坐标轴所围面积可知第二次面积大于第一次面积,故第二次在竖直方向上的位移比第一次的大,A错误;因为位移方向不变,而第二次竖直位移大,故第二次水平位移也大,B正确;第一次竖直方向速度变化量大,经历时间短,由知,,因此C错误;在竖直方向上根据牛顿第二定律mg-Ff=ma,知加速度大的阻力小,D正确。
【答案】BD
8.【解析】小球从a点以初速度沿ab方向抛出若恰好落到最低点C点,竖直方向:,
水平方向:,联立上述两式可得,掉到环上时的竖直分速度为,当h=g时,掉到环上时的竖直分速度最大,A项正确;当小球的初速度时,将撞击到环上的圆弧ac段,B项正确;若小球可以垂直撞击圆环,则其速度的反向延长线一定通过圆心O,则圆心O为小球做平抛运动的水平位移的中点,而无论取何值,当小球落在圆环上时的水平位移都不可能为2R,故小球都不可能垂直撞击圆环,D项正确,C项错。
【答案】ABD
9.【解析】小球做平抛运动,将小球打在斜坡上的速度分解如图所示,由几何关系可得水平方向小球做匀速直线运动,则有位移①;竖直方向小球做自由落体运动,有②,③联立上述三式解得,,。小球B从同一点Q处自由下落至P点的过程中有,解得,故,D项正确。
【答案】D
10.
【解析】(1)设运动员做平抛运动落到b点所需时间为t1,则Lsin
30°=,解得t1=2
s;
(2)从a点飞出的速度大小v0==10
m/s;
(3)将运动员实际的运动看作平行斜面方向和垂直斜面方向这两个分运动的合运动
垂直斜面方向:初速度v01=v0sin
30°=5
m/s,
加速度a1=-gcos
30°=-5
m/s2
经过时间t,垂直斜面的分速度v1=v01+a1t
当v1=0,即t=1
s时,物体距离斜面最远
最远距离d=v01t+a1t2=
m。
【答案】(1)2
s (2)10
m/s (3)
m
6
