11.3.2 多边形的内角和 2020年暑假预习人教版数学八年级上册知识点归纳与同步练习(含答案)
文档属性
| 名称 | 11.3.2 多边形的内角和 2020年暑假预习人教版数学八年级上册知识点归纳与同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 368.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-14 00:00:00 | ||
图片预览


文档简介
第11章 三角形
多边形的内角和
多边形的内角和公式:n边形的内角和等于(n-2)×180°。
多边形的内角和推理方法
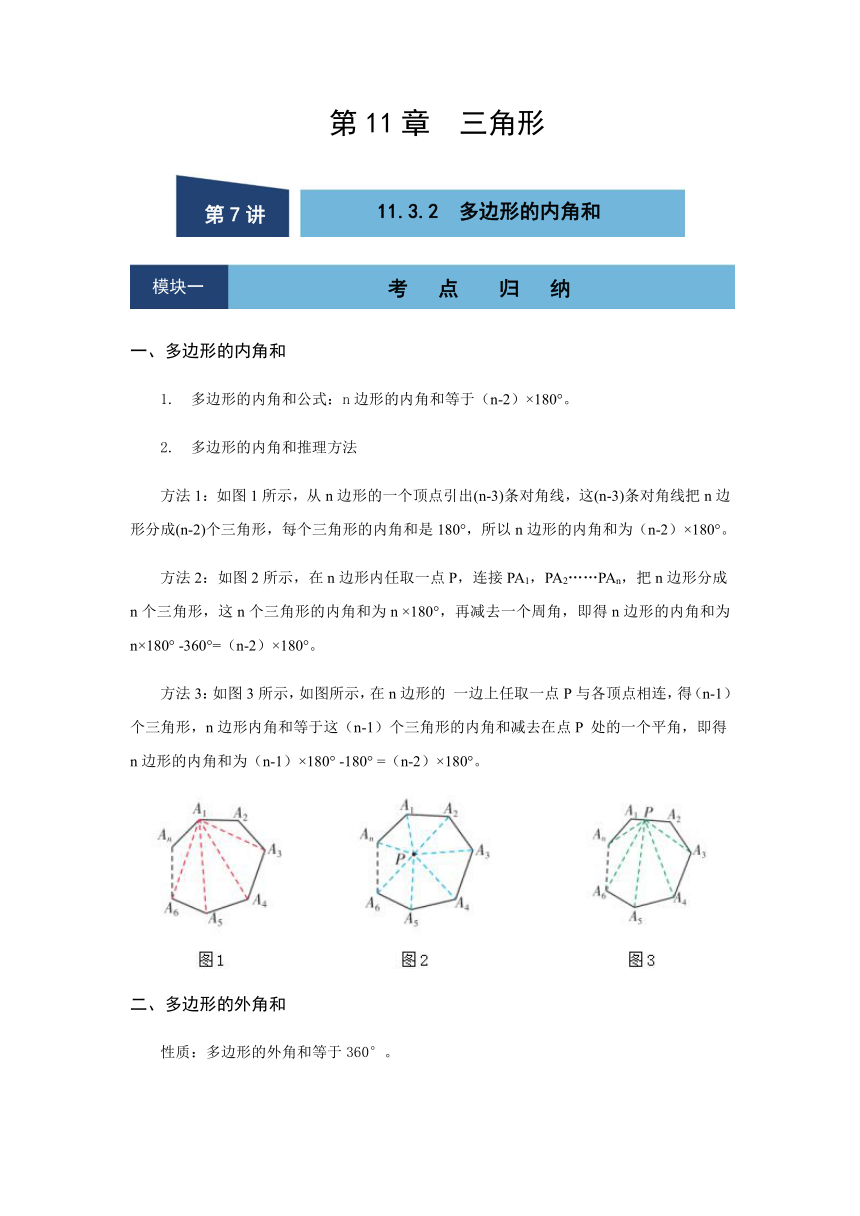
方法1:如图1所示,从n边形的一个顶点引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形,每个三角形的内角和是180°,所以n边形的内角和为(n-2)×180°。
方法2:如图2所示,在n边形内任取一点P,连接PA1,PA2……PAn,把n边形分成n个三角形,这n个三角形的内角和为n ×180°,再减去一个周角,即得n边形的内角和为n×180° -360°=(n-2)×180°。
方法3:如图3所示,如图所示,在n边形的 一边上任取一点P与各顶点相连,得(n-1)个三角形,n边形内角和等于这(n-1)个三角形的内角和减去在点P 处的一个平角,即得n边形的内角和为(n-1)×180° -180° =(n-2)×180°。
多边形的外角和
性质:多边形的外角和等于360°。
一.选择题(共10小题)
1.正十二边形的一个内角的度数为
A. B. C. D.
2.如果一个多边形的内角和等于一个三角形的外角和,那么这个多边形是
A.三角形 B.四边形 C.五边形 D.六边形
3.有一个正多边形,它的内角和等于外角和,那么这个正多边形的边数是
A.8 B.6 C.4 D.3
4.已知正多边形的一个内角是,则这个正多边形的边数是
A.九 B.八 C.七 D.六
5.若正多边形的内角和是,则该正多边形的一个外角为
A. B. C. D.
6.如图,正五边形绕点旋转了,当时,则
A. B. C. D.
第6题 第8题
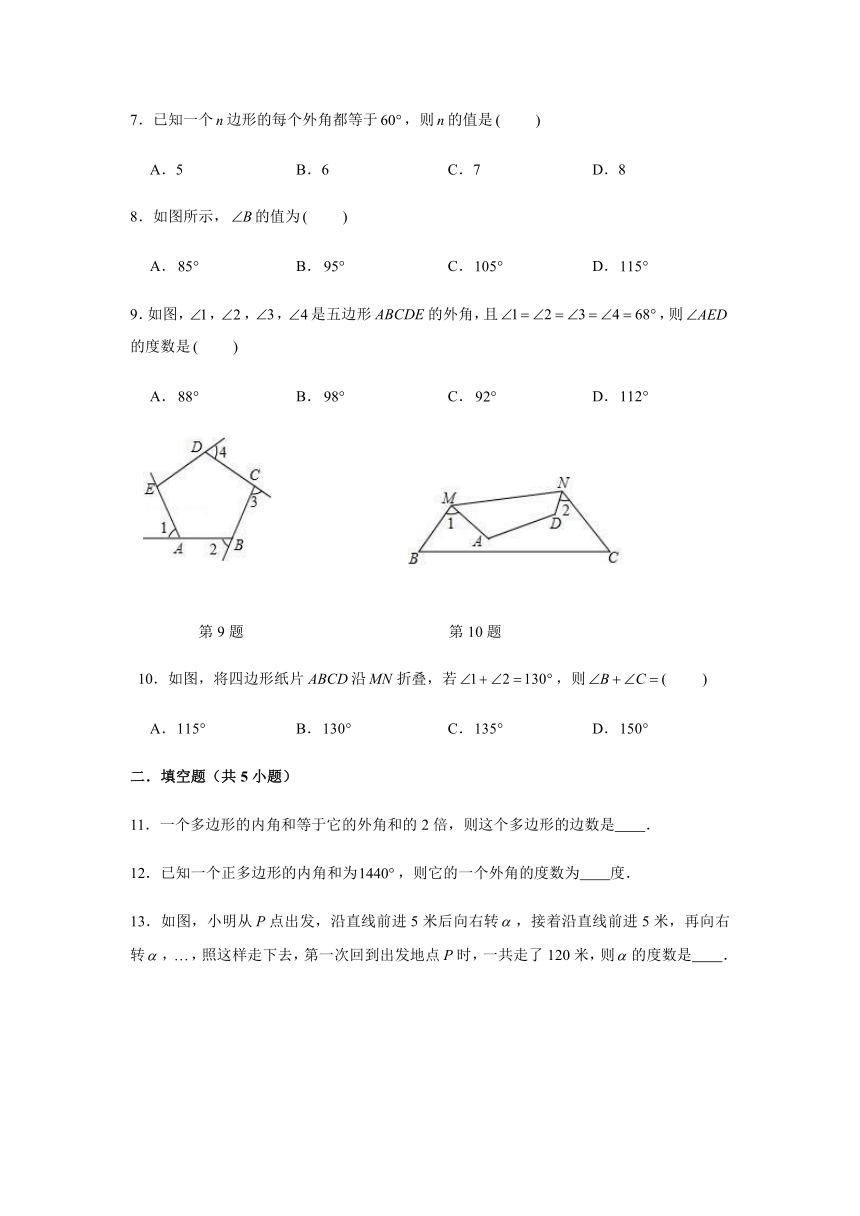
7.已知一个边形的每个外角都等于,则的值是
A.5 B.6 C.7 D.8
8.如图所示,的值为
A. B. C. D.
9.如图,,,,是五边形的外角,且,则的度数是
A. B. C. D.
第9题 第10题
10.如图,将四边形纸片沿折叠,若,则
A. B. C. D.
二.填空题(共5小题)
11.一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是 .
12.已知一个正多边形的内角和为,则它的一个外角的度数为 度.
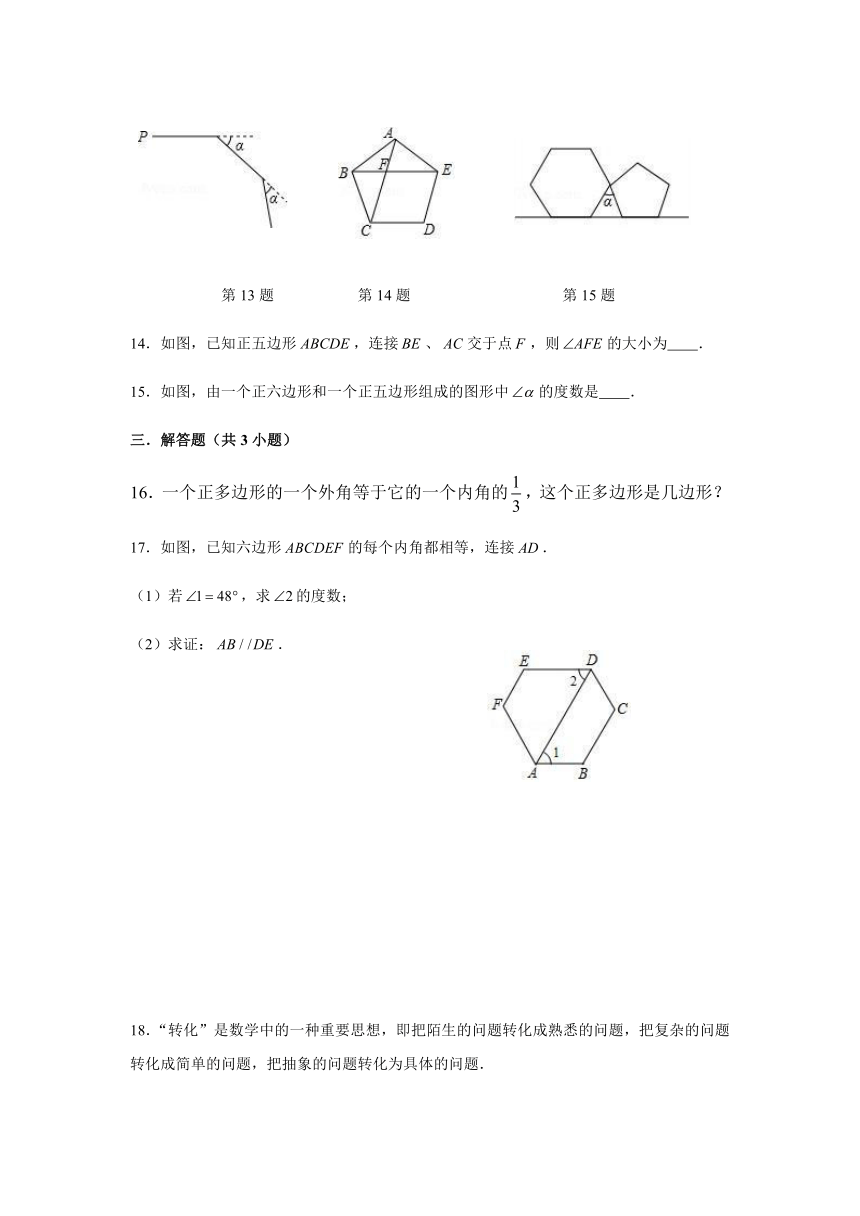
13.如图,小明从点出发,沿直线前进5米后向右转,接着沿直线前进5米,再向右转,,照这样走下去,第一次回到出发地点时,一共走了120米,则的度数是 .
第13题 第14题 第15题
14.如图,已知正五边形,连接、交于点,则的大小为 .
15.如图,由一个正六边形和一个正五边形组成的图形中的度数是 .
三.解答题(共3小题)
16.一个正多边形的一个外角等于它的一个内角的,这个正多边形是几边形?
17.如图,已知六边形的每个内角都相等,连接.
(1)若,求的度数;
(2)求证:.
18.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的的度数吗?只要写出结论,不需要写出解题过程)
选择题(共 10 小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C A B C B D C A
二.填空题(共5小题)
11.6.
12.36.
13..
14..
15..
三.解答题(共3小题)
16.解: 设外角为,则内角为,由题意得:
,
解得:,
,
答: 这个正多边形为八边形 .
17.解:(1)六边形的各内角相等,
一个内角的大小为,
.
,,
.
,,
.
(2)证明:,
,
,
.
18.解:(1),,
;
(2),,
;
(3)根据图中可得出规律,每截去一个角则会增加180度,
所以当截去5个角时增加了度,
则.
声明:试题解析著作权属所有,未经书面同意,不得复制发布:2020/7/14 16:12:58;用户:liumr80;邮箱:liumr80@;学号:4865871
多边形的内角和
多边形的内角和公式:n边形的内角和等于(n-2)×180°。
多边形的内角和推理方法
方法1:如图1所示,从n边形的一个顶点引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形,每个三角形的内角和是180°,所以n边形的内角和为(n-2)×180°。
方法2:如图2所示,在n边形内任取一点P,连接PA1,PA2……PAn,把n边形分成n个三角形,这n个三角形的内角和为n ×180°,再减去一个周角,即得n边形的内角和为n×180° -360°=(n-2)×180°。
方法3:如图3所示,如图所示,在n边形的 一边上任取一点P与各顶点相连,得(n-1)个三角形,n边形内角和等于这(n-1)个三角形的内角和减去在点P 处的一个平角,即得n边形的内角和为(n-1)×180° -180° =(n-2)×180°。
多边形的外角和
性质:多边形的外角和等于360°。
一.选择题(共10小题)
1.正十二边形的一个内角的度数为
A. B. C. D.
2.如果一个多边形的内角和等于一个三角形的外角和,那么这个多边形是
A.三角形 B.四边形 C.五边形 D.六边形
3.有一个正多边形,它的内角和等于外角和,那么这个正多边形的边数是
A.8 B.6 C.4 D.3
4.已知正多边形的一个内角是,则这个正多边形的边数是
A.九 B.八 C.七 D.六
5.若正多边形的内角和是,则该正多边形的一个外角为
A. B. C. D.
6.如图,正五边形绕点旋转了,当时,则
A. B. C. D.
第6题 第8题
7.已知一个边形的每个外角都等于,则的值是
A.5 B.6 C.7 D.8
8.如图所示,的值为
A. B. C. D.
9.如图,,,,是五边形的外角,且,则的度数是
A. B. C. D.
第9题 第10题
10.如图,将四边形纸片沿折叠,若,则
A. B. C. D.
二.填空题(共5小题)
11.一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是 .
12.已知一个正多边形的内角和为,则它的一个外角的度数为 度.
13.如图,小明从点出发,沿直线前进5米后向右转,接着沿直线前进5米,再向右转,,照这样走下去,第一次回到出发地点时,一共走了120米,则的度数是 .
第13题 第14题 第15题
14.如图,已知正五边形,连接、交于点,则的大小为 .
15.如图,由一个正六边形和一个正五边形组成的图形中的度数是 .
三.解答题(共3小题)
16.一个正多边形的一个外角等于它的一个内角的,这个正多边形是几边形?
17.如图,已知六边形的每个内角都相等,连接.
(1)若,求的度数;
(2)求证:.
18.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的的度数吗?只要写出结论,不需要写出解题过程)
选择题(共 10 小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C A B C B D C A
二.填空题(共5小题)
11.6.
12.36.
13..
14..
15..
三.解答题(共3小题)
16.解: 设外角为,则内角为,由题意得:
,
解得:,
,
答: 这个正多边形为八边形 .
17.解:(1)六边形的各内角相等,
一个内角的大小为,
.
,,
.
,,
.
(2)证明:,
,
,
.
18.解:(1),,
;
(2),,
;
(3)根据图中可得出规律,每截去一个角则会增加180度,
所以当截去5个角时增加了度,
则.
声明:试题解析著作权属所有,未经书面同意,不得复制发布:2020/7/14 16:12:58;用户:liumr80;邮箱:liumr80@;学号:4865871
