24.2.1点和圆的位置关系-人教版九年级数学上册课件(共19张PPT)
文档属性
| 名称 | 24.2.1点和圆的位置关系-人教版九年级数学上册课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-14 10:40:20 | ||
图片预览






文档简介
(共19张PPT)
点和圆的位置关系
二十四章
24.2.1
1、教学目标
2、教学重点
3、教学难点
4、教学过程
5、小
结
点和圆的位置关系
教学目标:
1、理解并掌握圆O的半径为r,点A到圆心的距离OA=d,则有:点A在圆上等价于d=r;点A在圆内等价于dr及其运用。
2、理解不在同一直线上的三个点确定一个圆并掌握他的运用。
教学难点:
教学重点:
点与圆的位置关系的判断。
探究三点作圆的过程,明白同一条直线不能做圆的道理。
2008年北京奥运会在2008年8月8日晚上8时整在北京正式开幕。此次奥运会共有参赛国家及地区204个,参赛运动员11438人,设302项(28种)运动,其中一种运动就是射箭(archery)。
射箭是用弓把箭射出并射中预定目标,打在靶上的技艺。
了解一下:
视频
小明了解了射箭运动之后,积极地参加了学校的射箭比赛,小明射出了三根箭,射击情况分别如下:
1、小明的第一支箭脱靶了。
思考:
2、小明的第二支箭恰好射到了标靶边缘。
3、小明的第三支箭射在了距离靶心很近的位置。
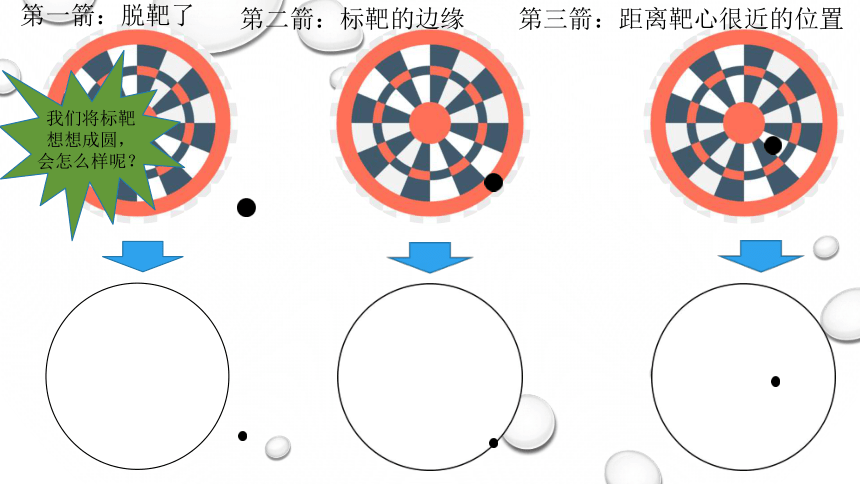
我们不妨把箭靶看成同心圆;把箭头看成一个点,这样我们就可以把小明的三次射箭情况画到纸上:
小明哪次射的最好呢?
第一箭:脱靶了
第二箭:标靶的边缘
第三箭:距离靶心很近的位置
我们将标靶想想成圆,会怎么样呢?
观察
我们观察图1,我们会发现这个圆把一个平面分成了A、B两份。在A部分的点我们称为在圆外的点;在B部分的点我们称为在圆内的点;在圆周上的点我们称之为在圆上的点。
A
B
图1
圆内的点
圆外的点
圆上的点
再来看一下小明的第一箭:
小明的第一箭脱靶了,所以箭头落在了圆的外面,也就是说点在⊙O外。
O
A
其中⊙O的半径是r;点O到点A的距离是d
r
d
我们明显的可以比较出来:d>r
所以我们就有:
点A在⊙O外
d>r
小明的第二支箭:
小明的第二支箭恰好射中了标靶边缘,也就是说点A在⊙O上。
A
O
r
d
其中⊙O的半径是r;点O到点A的距离是d
OA也是⊙O的一个半径,我们得知:d=r
所以我们就有:
点A在⊙
O上
d=r
小明的第三支箭:
小明的第三支箭正好射中了离靶心很近的位置,也就是说点A在⊙O内。
O
A
其中⊙O的半径是r;点O到点A的距离是d
r
d
显然,我们可以看出:d所以我们就有:
点A在⊙O内
dr
d点A在⊙O内
d=r
点A在⊙
O上
d>r
点A在⊙O外
总结点与圆的位置关系:
符号
读作“等价于”,它表示从符号
的左端可以得到右端;从右端也可以得到左端.
1:⊙O的半径15cm,A、B、C三点到圆心的距离分别为8cm、15cm、22cm,则点A、B、C与⊙O的位置关系是:
点A在
.
点B在
.
点C在
.
牛刀小试
∵OA=8<15
∴点A在圆内
∵OB=15=15
∴点B在圆上
∵OC=22>15
∴点C在圆外
圆内
圆上
圆外
2:在⊙O中,点A到⊙O的最小距离为3,最大距离是19,那么⊙O的半径为(
)
N
O
M
A
19
3
A
O
3
19
M
N
11或8
NM=19-3=16
2R=16
R=8
NM=19+3=22
2R=22
R=11
回忆思考
1、过一点,可以画几条直线?
2、过两点可以画几条直线?
●A
●A
●B
直线公理:
过两点有且只有一条直线
3、过三个点能画几条直线?
回忆思考
过三点
1、若三点共线,则过这三点只能作一条直线.
A
B
C
2、若三点不共线,则过这三点不能作直线,但过任意其中两点一共可作三条直线.
C
B
A
探索
1、过一个点可以画多少个圆呢?
2、过两个点可以画多少个圆呢
●A
●O
●O
●O
●O
●O
A
B
●O
●
O
●O
无数个
无数个
┓
●B
●C
经过B,C两点的圆的圆心在线段AB的垂直平分线上.
┏
●A
经过A,B,C三点的圆的圆心应该这两条垂直平分线的交点O的位置.
●O
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
探索
3、过三个点可以画多少个圆呢?
动画
不在同一条直线上的三个点确定一个圆。
谢
谢
观
看
再
见!
点和圆的位置关系
二十四章
24.2.1
1、教学目标
2、教学重点
3、教学难点
4、教学过程
5、小
结
点和圆的位置关系
教学目标:
1、理解并掌握圆O的半径为r,点A到圆心的距离OA=d,则有:点A在圆上等价于d=r;点A在圆内等价于d
2、理解不在同一直线上的三个点确定一个圆并掌握他的运用。
教学难点:
教学重点:
点与圆的位置关系的判断。
探究三点作圆的过程,明白同一条直线不能做圆的道理。
2008年北京奥运会在2008年8月8日晚上8时整在北京正式开幕。此次奥运会共有参赛国家及地区204个,参赛运动员11438人,设302项(28种)运动,其中一种运动就是射箭(archery)。
射箭是用弓把箭射出并射中预定目标,打在靶上的技艺。
了解一下:
视频
小明了解了射箭运动之后,积极地参加了学校的射箭比赛,小明射出了三根箭,射击情况分别如下:
1、小明的第一支箭脱靶了。
思考:
2、小明的第二支箭恰好射到了标靶边缘。
3、小明的第三支箭射在了距离靶心很近的位置。
我们不妨把箭靶看成同心圆;把箭头看成一个点,这样我们就可以把小明的三次射箭情况画到纸上:
小明哪次射的最好呢?
第一箭:脱靶了
第二箭:标靶的边缘
第三箭:距离靶心很近的位置
我们将标靶想想成圆,会怎么样呢?
观察
我们观察图1,我们会发现这个圆把一个平面分成了A、B两份。在A部分的点我们称为在圆外的点;在B部分的点我们称为在圆内的点;在圆周上的点我们称之为在圆上的点。
A
B
图1
圆内的点
圆外的点
圆上的点
再来看一下小明的第一箭:
小明的第一箭脱靶了,所以箭头落在了圆的外面,也就是说点在⊙O外。
O
A
其中⊙O的半径是r;点O到点A的距离是d
r
d
我们明显的可以比较出来:d>r
所以我们就有:
点A在⊙O外
d>r
小明的第二支箭:
小明的第二支箭恰好射中了标靶边缘,也就是说点A在⊙O上。
A
O
r
d
其中⊙O的半径是r;点O到点A的距离是d
OA也是⊙O的一个半径,我们得知:d=r
所以我们就有:
点A在⊙
O上
d=r
小明的第三支箭:
小明的第三支箭正好射中了离靶心很近的位置,也就是说点A在⊙O内。
O
A
其中⊙O的半径是r;点O到点A的距离是d
r
d
显然,我们可以看出:d
点A在⊙O内
d
d
d=r
点A在⊙
O上
d>r
点A在⊙O外
总结点与圆的位置关系:
符号
读作“等价于”,它表示从符号
的左端可以得到右端;从右端也可以得到左端.
1:⊙O的半径15cm,A、B、C三点到圆心的距离分别为8cm、15cm、22cm,则点A、B、C与⊙O的位置关系是:
点A在
.
点B在
.
点C在
.
牛刀小试
∵OA=8<15
∴点A在圆内
∵OB=15=15
∴点B在圆上
∵OC=22>15
∴点C在圆外
圆内
圆上
圆外
2:在⊙O中,点A到⊙O的最小距离为3,最大距离是19,那么⊙O的半径为(
)
N
O
M
A
19
3
A
O
3
19
M
N
11或8
NM=19-3=16
2R=16
R=8
NM=19+3=22
2R=22
R=11
回忆思考
1、过一点,可以画几条直线?
2、过两点可以画几条直线?
●A
●A
●B
直线公理:
过两点有且只有一条直线
3、过三个点能画几条直线?
回忆思考
过三点
1、若三点共线,则过这三点只能作一条直线.
A
B
C
2、若三点不共线,则过这三点不能作直线,但过任意其中两点一共可作三条直线.
C
B
A
探索
1、过一个点可以画多少个圆呢?
2、过两个点可以画多少个圆呢
●A
●O
●O
●O
●O
●O
A
B
●O
●
O
●O
无数个
无数个
┓
●B
●C
经过B,C两点的圆的圆心在线段AB的垂直平分线上.
┏
●A
经过A,B,C三点的圆的圆心应该这两条垂直平分线的交点O的位置.
●O
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
探索
3、过三个点可以画多少个圆呢?
动画
不在同一条直线上的三个点确定一个圆。
谢
谢
观
看
再
见!
同课章节目录
