北师大版高中数学必修一1.3.1《集合的基本运算》教案(第一课时)
文档属性
| 名称 | 北师大版高中数学必修一1.3.1《集合的基本运算》教案(第一课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-17 00:00:00 | ||
图片预览

文档简介
1.3.1
集合的基本运算
教学目的:(1)理解两个集合的并集与交集的的含义,会求两个简单集合的并集与交集;
(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;(3)能用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用。
课
型:新授课
教学重点:集合的交集与并集、补集的概念;
教学难点:集合的交集与并集、补集“是什么”,“为什么”,“怎样做”;
第一课时:
教学过程:
1、
引入课题
我们两个实数之间可以进行运算,比如加法运算,那么两个集合之间存在运算吗?
实例1:A=﹛高一(9)班女生﹜
B=﹛高一(9)班团员﹜
C=﹛高一(9)班女团员﹜,我们发现集合C中的元素是集合A和集合B的公共元素。
实例2:学校的某次运动会要求各班选出数名篮球队员和足球队员
假设A=﹛高一(9)班的篮球队员﹜B=﹛高一(9)班的足球队员﹜
C=﹛高一(9)班的运动员﹜,我们发现集合C的元素是由集合A和集合B的元素共同构成的。
我们发现集合之间是存在一定运算的。
2、
新课教学
1.交集(如实例1)
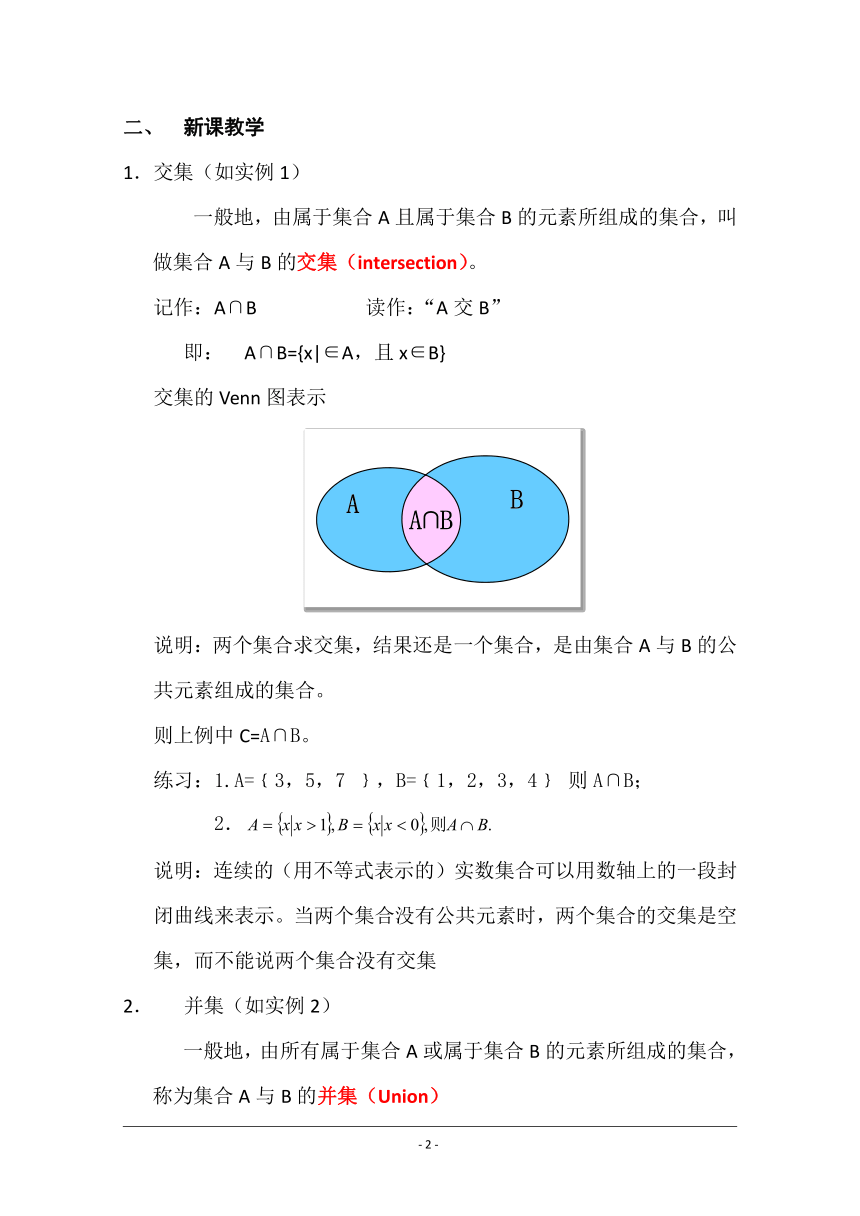
一般地,由属于集合A且属于集合B的元素所组成的集合,叫做集合A与B的交集(intersection)。
记作:A∩B
读作:“A交B”
即:
A∩B={x|∈A,且x∈B}
交集的Venn图表示
说明:两个集合求交集,结果还是一个集合,是由集合A与B的公共元素组成的集合。
则上例中C=A∩B。
练习:1.A=﹛3,5,7
﹜,B=﹛1,2,3,4﹜
则A∩B;
2.
说明:连续的(用不等式表示的)实数集合可以用数轴上的一段封闭曲线来表示。当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集
2.
并集(如实例2)
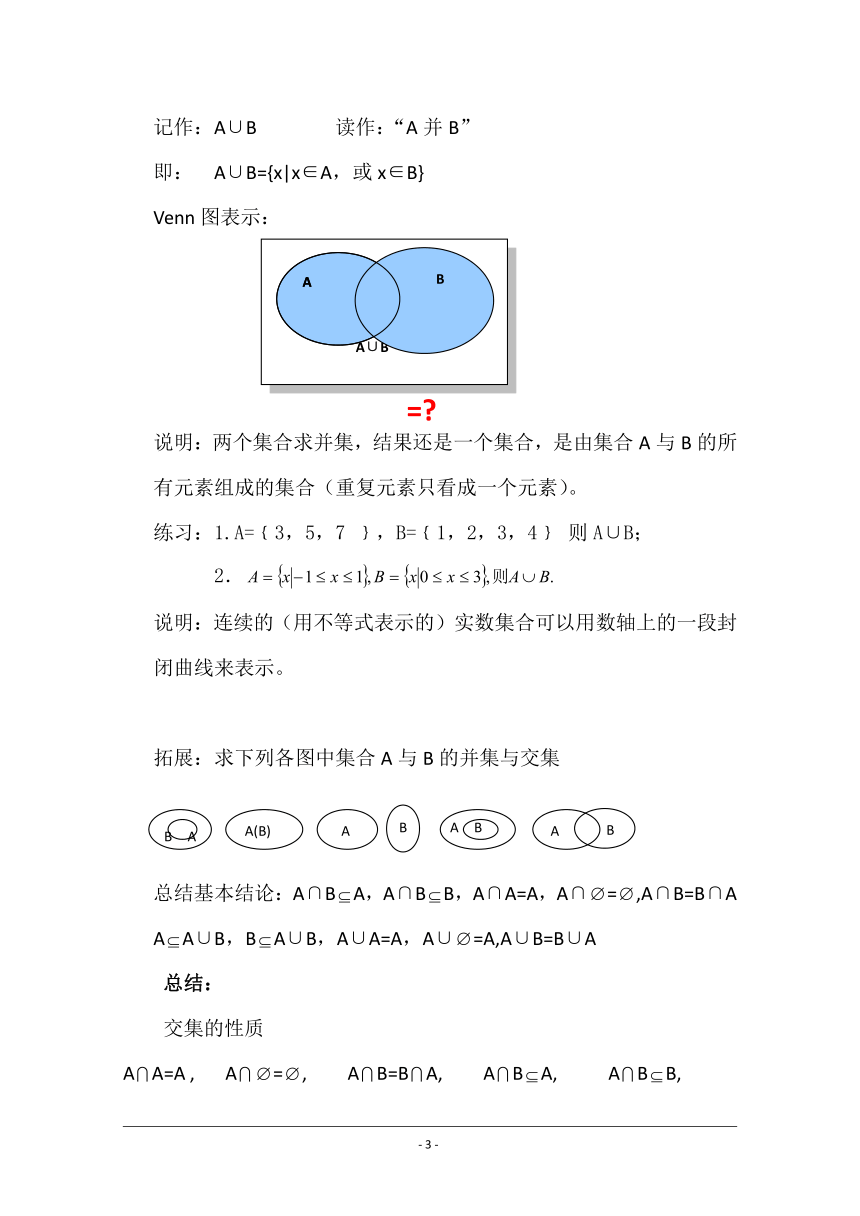
一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(Union)
记作:A∪B
读作:“A并B”
即:
A∪B={x|x∈A,或x∈B}
Venn图表示:
说明:两个集合求并集,结果还是一个集合,是由集合A与B的所有元素组成的集合(重复元素只看成一个元素)。
练习:1.A=﹛3,5,7
﹜,B=﹛1,2,3,4﹜
则A∪B;
2.
说明:连续的(用不等式表示的)实数集合可以用数轴上的一段封闭曲线来表示。
拓展:求下列各图中集合A与B的并集与交集
总结基本结论:A∩BA,A∩BB,A∩A=A,A∩=,A∩B=B∩A
AA∪B,BA∪B,A∪A=A,A∪=A,A∪B=B∪A
总结:
交集的性质
AA=A
,
A=,
AB=BA,
ABA,
ABB,
若AB,则AB=A,反之也成立。
并集的性质
AA=A,
A=A,
AB=BA,
ABA,
ABB
若AB,则AB=B,反之也成立。
联系交集的性质有结论:ABAAB.
三.例题讲解:
例1.某学校所有男生组成的集合A,一年级的所有学生组成的集合B,一年级的所有男生组成的集合C,一年级的所有女生组成的集合D,求A∩B,C∪D。
解
A∩B=
=B.
例2.设
求A∩B,A∪B.
解
完成思考交流,通过文氏图说明。总结集合的交集和并集运算满足结合律。
例3.
已知集合M={y|y=x2+1,x∈R},N={y|y=x+1,x∈R},求M∩N。
解
M={y|y=x2+1,x∈R}={y|y≥1},N={y|y=x+1,x∈R}={y|y∈R}
∴
M∩N=M={y|y≥1}
四.课堂练习:
P12
练习
1,2,3,4题P14习题1题
五.小结:
A∩B={x|∈A,且x∈B}
A∪B={x|x∈A,或x∈B}
交集的性质
AA=A
,
A=,
AB=BA,
ABA,
ABB,
若AB,则AB=A,反之也成立。
并集的性质
AA=A,
A=A,
AB=BA,
ABA,
ABB
若AB,则AB=B,反之也成立。
联系交集的性质有结论:ABAAB.
六.作业
1.基础作业:P14习题A组2,3,4题
2.选做:
已知集合A={x|x2-3x+2=0},B={x|x2-mx+2=0},且A∩B=B,求实数m范围。
解
化简条件得A={1,2},A∩B=BBA
根据集合中元素个数集合B分类讨论,B=,B={1}或{2},B={1,2}
当B=时,△=m2-8<0
∴
当B={1}或{2}时,,m无解
当B={1,2}时,
∴
m=3
综上所述,m=3或
3.思考B组1题
A∪B
A
B
A
=?
A
B
A(B)
A
B
B
A
B
A
PAGE
-
6
-
集合的基本运算
教学目的:(1)理解两个集合的并集与交集的的含义,会求两个简单集合的并集与交集;
(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;(3)能用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用。
课
型:新授课
教学重点:集合的交集与并集、补集的概念;
教学难点:集合的交集与并集、补集“是什么”,“为什么”,“怎样做”;
第一课时:
教学过程:
1、
引入课题
我们两个实数之间可以进行运算,比如加法运算,那么两个集合之间存在运算吗?
实例1:A=﹛高一(9)班女生﹜
B=﹛高一(9)班团员﹜
C=﹛高一(9)班女团员﹜,我们发现集合C中的元素是集合A和集合B的公共元素。
实例2:学校的某次运动会要求各班选出数名篮球队员和足球队员
假设A=﹛高一(9)班的篮球队员﹜B=﹛高一(9)班的足球队员﹜
C=﹛高一(9)班的运动员﹜,我们发现集合C的元素是由集合A和集合B的元素共同构成的。
我们发现集合之间是存在一定运算的。
2、
新课教学
1.交集(如实例1)
一般地,由属于集合A且属于集合B的元素所组成的集合,叫做集合A与B的交集(intersection)。
记作:A∩B
读作:“A交B”
即:
A∩B={x|∈A,且x∈B}
交集的Venn图表示
说明:两个集合求交集,结果还是一个集合,是由集合A与B的公共元素组成的集合。
则上例中C=A∩B。
练习:1.A=﹛3,5,7
﹜,B=﹛1,2,3,4﹜
则A∩B;
2.
说明:连续的(用不等式表示的)实数集合可以用数轴上的一段封闭曲线来表示。当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集
2.
并集(如实例2)
一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(Union)
记作:A∪B
读作:“A并B”
即:
A∪B={x|x∈A,或x∈B}
Venn图表示:
说明:两个集合求并集,结果还是一个集合,是由集合A与B的所有元素组成的集合(重复元素只看成一个元素)。
练习:1.A=﹛3,5,7
﹜,B=﹛1,2,3,4﹜
则A∪B;
2.
说明:连续的(用不等式表示的)实数集合可以用数轴上的一段封闭曲线来表示。
拓展:求下列各图中集合A与B的并集与交集
总结基本结论:A∩BA,A∩BB,A∩A=A,A∩=,A∩B=B∩A
AA∪B,BA∪B,A∪A=A,A∪=A,A∪B=B∪A
总结:
交集的性质
AA=A
,
A=,
AB=BA,
ABA,
ABB,
若AB,则AB=A,反之也成立。
并集的性质
AA=A,
A=A,
AB=BA,
ABA,
ABB
若AB,则AB=B,反之也成立。
联系交集的性质有结论:ABAAB.
三.例题讲解:
例1.某学校所有男生组成的集合A,一年级的所有学生组成的集合B,一年级的所有男生组成的集合C,一年级的所有女生组成的集合D,求A∩B,C∪D。
解
A∩B=
=B.
例2.设
求A∩B,A∪B.
解
完成思考交流,通过文氏图说明。总结集合的交集和并集运算满足结合律。
例3.
已知集合M={y|y=x2+1,x∈R},N={y|y=x+1,x∈R},求M∩N。
解
M={y|y=x2+1,x∈R}={y|y≥1},N={y|y=x+1,x∈R}={y|y∈R}
∴
M∩N=M={y|y≥1}
四.课堂练习:
P12
练习
1,2,3,4题P14习题1题
五.小结:
A∩B={x|∈A,且x∈B}
A∪B={x|x∈A,或x∈B}
交集的性质
AA=A
,
A=,
AB=BA,
ABA,
ABB,
若AB,则AB=A,反之也成立。
并集的性质
AA=A,
A=A,
AB=BA,
ABA,
ABB
若AB,则AB=B,反之也成立。
联系交集的性质有结论:ABAAB.
六.作业
1.基础作业:P14习题A组2,3,4题
2.选做:
已知集合A={x|x2-3x+2=0},B={x|x2-mx+2=0},且A∩B=B,求实数m范围。
解
化简条件得A={1,2},A∩B=BBA
根据集合中元素个数集合B分类讨论,B=,B={1}或{2},B={1,2}
当B=时,△=m2-8<0
∴
当B={1}或{2}时,,m无解
当B={1,2}时,
∴
m=3
综上所述,m=3或
3.思考B组1题
A∪B
A
B
A
=?
A
B
A(B)
A
B
B
A
B
A
PAGE
-
6
-
