新人教数学 9年级下:达标训练(29.1投影)
文档属性
| 名称 | 新人教数学 9年级下:达标训练(29.1投影) |

|
|
| 格式 | zip | ||
| 文件大小 | 466.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-24 00:00:00 | ||
图片预览

文档简介
达标训练
基础 巩固
1.如图29.1-13,身高为1.6 m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2 m,CA=0.8 m,则树的高度为( )
图29.1-13
A.4.8 m B.6.4 m C.8 m D.10 m
思路解析:太阳光下,同一时刻不同物体及影长与光线构成的三角形是相似的.
设树高为x m,则1.6∶x=0.8∶(0.8+3.2),解得x=8.
答案:C
2.如图29.1-14是王芳同学某一天观察到的一棵树在不同时刻的影子,请你把它们按时间先后顺序进行排列,并说明理由.
图29.1-14
思路解析:早上太阳从东方升起,树的投影落在树的西方(图B);傍晚在西方落下,树的投影在树的东方(图D),从升起到落下的过程中,相当于太阳从东到南到西,树的投影相应从西到北到东.
答案:时间顺序为B、A、C、D.
理由如下:太阳从升起到落下的过程中,相当于太阳从东到南到西,树的投影相应从西到北到东移动.
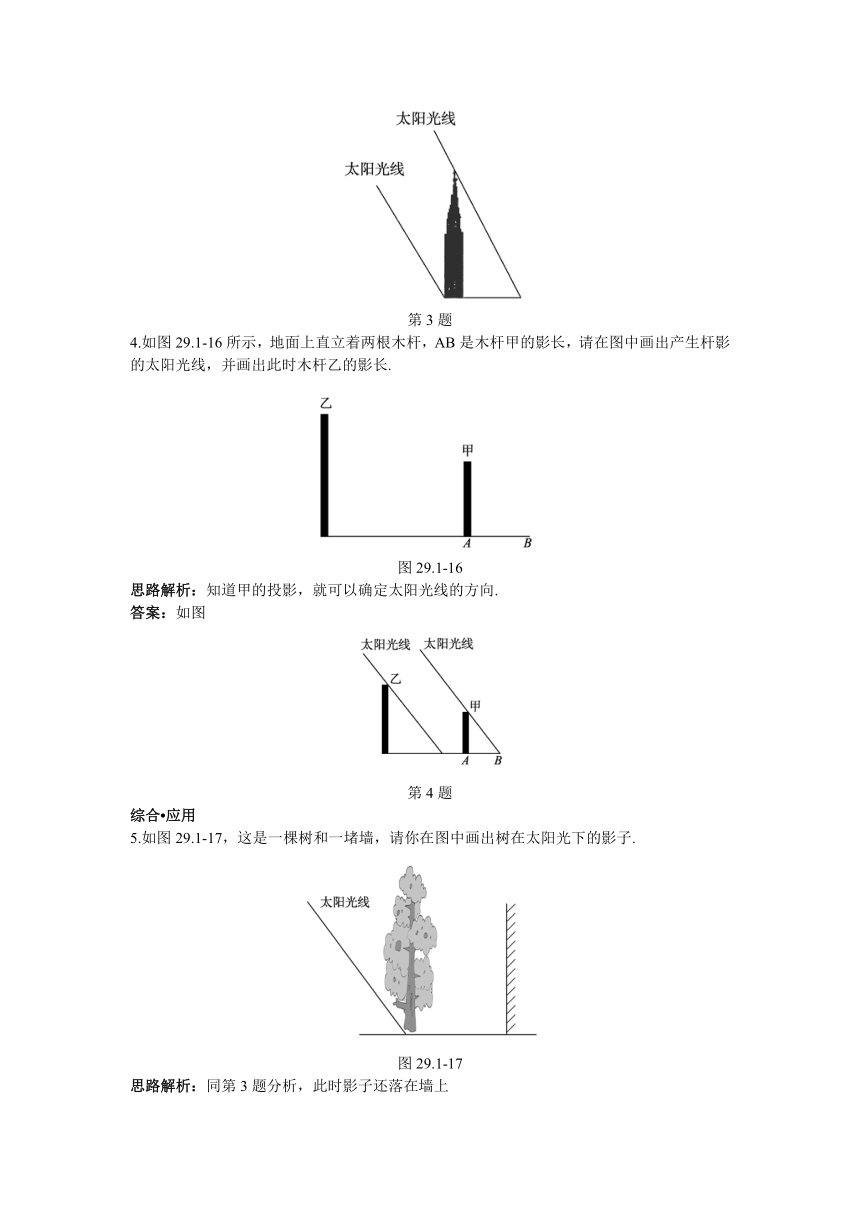
3.如图29.1-15是一座塔楼,请在图中画出它在太阳光下的影长.
图29.1-15
思路解析:太阳光是平行光线,过塔顶作已知太阳光线的平行线就是过塔顶的太阳光线.
答案:如图
第3题
4.如图29.1-16所示,地面上直立着两根木杆,AB是木杆甲的影长,请在图中画出产生杆影的太阳光线,并画出此时木杆乙的影长.
图29.1-16
思路解析:知道甲的投影,就可以确定太阳光线的方向.
答案:如图
第4题
综合 应用
5.如图29.1-17,这是一棵树和一堵墙,请你在图中画出树在太阳光下的影子.
图29.1-17
思路解析:同第3题分析,此时影子还落在墙上
答案:如图
第5题
6.画出如图29.1-18水平摆放的正四棱锥在竖直放置的投影面P上的正投影.
图29.1-18
(1)正四棱锥的棱AB与投影面P平行;
(2)正四棱锥的棱AB与投影面P不平行.
思路解析:(1)当棱AB与投影面P平行时,由于底面ABCD与投影面P垂直,棱AB、CD的正投影是两条重合的,与棱本身相等的线段;棱BC、AD的正投影分别是两个点;棱PA、PB、PC、PD的正投影分别是比它们本身要短的线段,并且PA与PD、PB与PC的投影分别重合.所以,四棱锥的投影是三角形.
(2)当棱AB与投影面P不平行时,由于底面ABCD与投影面P垂直,所以底面ABCD的正投影是与对角线AC相等的线段;棱PA、PB、PC、PD的正投影分别是比它们本身要短的线段.
答案:(1)如图①;(2)如图②.
第6题① 第6题②
7.在太阳光照射下,如图29.1-19所示的图形中,哪些可以作为正方体的影子,将光源改为灯光将如何?
图29.1-19
思路解析:太阳光照射下,正方体的6个面都有投影,它们有时重合,有时不重合.
①当正方体的一个面平行于投影面时,正方体的正投影是正方形,斜投影是长方形;
②当正方体有一个面垂直于投影面,但每一个面不平行于投影面时,正方体的正投影是长方形;
③当正方体的每一个面不平行于投影面,且每一个面不垂直于投影面时,正方体的正投影是正六边形(此时正方体的6个顶点的投影都不重合).
灯光照射下,由于线段跟影长不成定比例,所以其投影还可能是梯形.
答案:(1)、(2)是太阳光照射下的影子,(1)、(2)、(3)是灯光照射下的影子.
回顾 展望
8.(2010山东淄博模拟) 如图29.1-20,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大1.5米 B.减小1.5米 C.增大3.5米 D.减小3.5米
思路解析:分别计算影长,比较变化量.
设小明在A处的影长为x米,则8:1.6=(x+20):x,解得x=5(米);同理,得到小明在B处的影长为1.5米.
答案:C
9.(山东泰州模拟) 高为12.6米的教学楼ED前有一棵大树AB(如图1).
图1 图2
(1)某一时刻测得大树AB、教学楼ED在阳光下的投影长分别是BC=2.4米,DF=7.2米,求大树AB的高度.
(2)用皮尺、高为h米的测角仪,请你设计另一种测量大树AB高度的方案,要求:
①在图2上,画出你设计的测量方案示意图,并将应测数据标记在图上(长度用字母m、n…表示,角度用希腊字母α、β…表示);
②根据你所画的示意图和标注的数据,计算大树AB高度(用字母表示).
思路解析:根据太阳光线下,同一时刻,影长与物高成比例计算.
测角仪可以测量不同位置,树的仰角,用解直角三角形的方法计算.
解:连接AC、EF.
(1)∵太阳光线是平行线,∴AC∥EF.∴∠ACB=∠EFD.
∵∠ABC=∠EDF=90°,∴△ABC∽△EDF.
∴.∴.∴AB=4.2.
答:大树AB的高是4.2米.
(2)(方法一
如图MG=BN=m,
AG=mtanα,∴AB=(mtanα+h)米.
(方法二)
∴,,∴.
∴.
∴(米).
基础 巩固
1.如图29.1-13,身高为1.6 m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2 m,CA=0.8 m,则树的高度为( )
图29.1-13
A.4.8 m B.6.4 m C.8 m D.10 m
思路解析:太阳光下,同一时刻不同物体及影长与光线构成的三角形是相似的.
设树高为x m,则1.6∶x=0.8∶(0.8+3.2),解得x=8.
答案:C
2.如图29.1-14是王芳同学某一天观察到的一棵树在不同时刻的影子,请你把它们按时间先后顺序进行排列,并说明理由.
图29.1-14
思路解析:早上太阳从东方升起,树的投影落在树的西方(图B);傍晚在西方落下,树的投影在树的东方(图D),从升起到落下的过程中,相当于太阳从东到南到西,树的投影相应从西到北到东.
答案:时间顺序为B、A、C、D.
理由如下:太阳从升起到落下的过程中,相当于太阳从东到南到西,树的投影相应从西到北到东移动.
3.如图29.1-15是一座塔楼,请在图中画出它在太阳光下的影长.
图29.1-15
思路解析:太阳光是平行光线,过塔顶作已知太阳光线的平行线就是过塔顶的太阳光线.
答案:如图
第3题
4.如图29.1-16所示,地面上直立着两根木杆,AB是木杆甲的影长,请在图中画出产生杆影的太阳光线,并画出此时木杆乙的影长.
图29.1-16
思路解析:知道甲的投影,就可以确定太阳光线的方向.
答案:如图
第4题
综合 应用
5.如图29.1-17,这是一棵树和一堵墙,请你在图中画出树在太阳光下的影子.
图29.1-17
思路解析:同第3题分析,此时影子还落在墙上
答案:如图
第5题
6.画出如图29.1-18水平摆放的正四棱锥在竖直放置的投影面P上的正投影.
图29.1-18
(1)正四棱锥的棱AB与投影面P平行;
(2)正四棱锥的棱AB与投影面P不平行.
思路解析:(1)当棱AB与投影面P平行时,由于底面ABCD与投影面P垂直,棱AB、CD的正投影是两条重合的,与棱本身相等的线段;棱BC、AD的正投影分别是两个点;棱PA、PB、PC、PD的正投影分别是比它们本身要短的线段,并且PA与PD、PB与PC的投影分别重合.所以,四棱锥的投影是三角形.
(2)当棱AB与投影面P不平行时,由于底面ABCD与投影面P垂直,所以底面ABCD的正投影是与对角线AC相等的线段;棱PA、PB、PC、PD的正投影分别是比它们本身要短的线段.
答案:(1)如图①;(2)如图②.
第6题① 第6题②
7.在太阳光照射下,如图29.1-19所示的图形中,哪些可以作为正方体的影子,将光源改为灯光将如何?
图29.1-19
思路解析:太阳光照射下,正方体的6个面都有投影,它们有时重合,有时不重合.
①当正方体的一个面平行于投影面时,正方体的正投影是正方形,斜投影是长方形;
②当正方体有一个面垂直于投影面,但每一个面不平行于投影面时,正方体的正投影是长方形;
③当正方体的每一个面不平行于投影面,且每一个面不垂直于投影面时,正方体的正投影是正六边形(此时正方体的6个顶点的投影都不重合).
灯光照射下,由于线段跟影长不成定比例,所以其投影还可能是梯形.
答案:(1)、(2)是太阳光照射下的影子,(1)、(2)、(3)是灯光照射下的影子.
回顾 展望
8.(2010山东淄博模拟) 如图29.1-20,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大1.5米 B.减小1.5米 C.增大3.5米 D.减小3.5米
思路解析:分别计算影长,比较变化量.
设小明在A处的影长为x米,则8:1.6=(x+20):x,解得x=5(米);同理,得到小明在B处的影长为1.5米.
答案:C
9.(山东泰州模拟) 高为12.6米的教学楼ED前有一棵大树AB(如图1).
图1 图2
(1)某一时刻测得大树AB、教学楼ED在阳光下的投影长分别是BC=2.4米,DF=7.2米,求大树AB的高度.
(2)用皮尺、高为h米的测角仪,请你设计另一种测量大树AB高度的方案,要求:
①在图2上,画出你设计的测量方案示意图,并将应测数据标记在图上(长度用字母m、n…表示,角度用希腊字母α、β…表示);
②根据你所画的示意图和标注的数据,计算大树AB高度(用字母表示).
思路解析:根据太阳光线下,同一时刻,影长与物高成比例计算.
测角仪可以测量不同位置,树的仰角,用解直角三角形的方法计算.
解:连接AC、EF.
(1)∵太阳光线是平行线,∴AC∥EF.∴∠ACB=∠EFD.
∵∠ABC=∠EDF=90°,∴△ABC∽△EDF.
∴.∴.∴AB=4.2.
答:大树AB的高是4.2米.
(2)(方法一
如图MG=BN=m,
AG=mtanα,∴AB=(mtanα+h)米.
(方法二)
∴,,∴.
∴.
∴(米).
