【数学】3.1.1《变化率问题》3.1.2《导数的概念》课件(人教a版选修1-1)
文档属性
| 名称 | 【数学】3.1.1《变化率问题》3.1.2《导数的概念》课件(人教a版选修1-1) |  | |
| 格式 | rar | ||
| 文件大小 | 425.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-25 04:17:18 | ||
图片预览








文档简介
(共27张PPT)
3.1.1 变化率问题
微积分主要与四类问题的处理相关:
一、已知物体运动的路程作为时间的函数,求物体在任意时刻的速度与加速度等;
二、求曲线的切线;
三、求已知函数的最大值与最小值;
四、求长度、面积、体积和重心等。
导数是微积分的核心概念之一,它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具。
问题1 气球膨胀率
在吹气球的过程中, 可发现,随着气球内空气容量的增加, 气球的半径增加得越来越慢. 从数学的角度, 如何描述这种现象呢
气球的体积V(单位:L)与半径r (单位:dm)之间的函数关系是
若将半径 r 表示为体积V的函数, 那么
当空气容量V从0L增加到1L , 气球半径增加了
气球的平均膨胀率为
当空气容量V从1L增加到2 L , 气球半径增加了
气球的平均膨胀率为
随着气球体积逐渐变大,它的平均膨胀率逐渐变小
思考
当空气容量从V1增加到V2时,气球的平均膨胀率是多少
问题2 高台跳水
在高台跳水运动中, 运动员相对于水面的高度 h (单位:m)与起跳后的时间 t (单位:s) 存在函数关系
如果用运动员在某段时间内的平均速度 描述其运动状态, 那么:
在0 ≤ t ≤0.5这段时间里,
在1≤ t ≤2这段时间里,
计算运动员在 这段时间里的平均速度,并思考下面的问题:
探
究:
(1) 运动员在这段时间里是静止的吗
(2) 你认为用平均速度描述运动员的运动状态有什么问题吗
平均速度不能反映他在这段时间里运动状态,
需要用瞬时速度描述运动状态。
定义:
平均变化率:
式子 称为函数 f (x)从x1到 x2的平均变化率.
令△x = x2 – x1 , △ f = f (x2) – f (x1) ,则
理解:
1,式子中△x 、△ f 的值可正、可负,但△x的值不能为0, △ f 的值可以为0
2,若函数f (x)为常函数时, △ f =0
3, 变式
思考
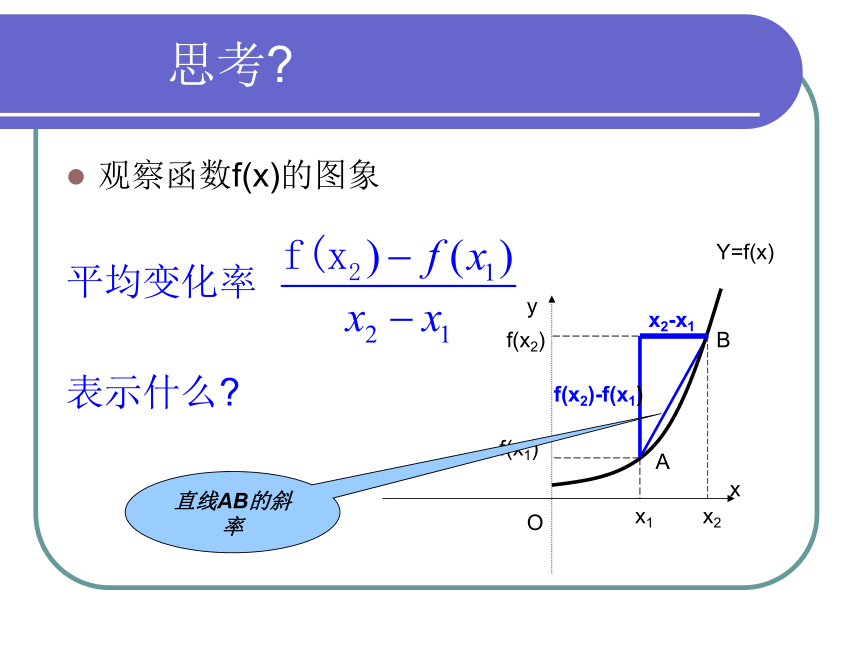
观察函数f(x)的图象
平均变化率
表示什么
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1
f(x2)-f(x1)
直线AB的斜率
练习:
1.甲用5年时间挣到10万元, 乙用5个月时间挣到2万元, 如何比较和评价甲、乙两人的经营成果
2.已知函数 f (x) = 2 x +1, g (x) = – 2 x, 分别计算在下列区间上 f (x) 及 g (x) 的平均变化率.
(1) [ –3 , –1] ; (2) [ 0 , 5 ] .
做两个题吧!
1 、已知函数f(x)=-x2+x的图象上的一点A(-1,-2)及临近一点B(-1+Δx,-2+Δy),则Δy/Δx=( )
A 3 B 3Δx-(Δx)2
C 3-(Δx)2 D 3-Δx
D
2、求y=x2在x=x0附近的平均速度。
2x0+Δx
小结:
1.函数的平均变化率
2.求函数的平均变化率的步骤:
(1)求函数的增量Δf=Δy=f(x2)-f(x1);
(2)计算平均变化率
3.1.2 导数的概念
在高台跳水运动中,平均速度不能反映他在这段时间里运动状态,需要用瞬时速度描述运动状态。我们把物体在某一时刻的速度称为瞬时速度.
又如何求
瞬时速度呢
平均变化率近似地刻画了曲线在某一区间上的变化趋势.
如何精确地刻画曲线在一点处的变化趋势呢
求:从2s到(2+△t)s这段时间内平均速度
△t<0时, 在[ 2+△t, 2 ]这段时
间内 △t>0时, 在[2, 2 +△t ]这段时间内
当△t = – 0.01时,
当△t = 0.01时,
当△t = – 0.001时,
当△t =0.001时,
当△t = –0.0001时,
当△t =0.0001时,
△t = – 0.00001,
△t = 0.00001,
△t = – 0.000001,
△t =0.000001,
……
……
平均变化率近似地刻画了曲线在某一区间上的变化趋势.
如何精确地刻画曲线在一点处的变化趋势呢
当△ t 趋近于0时, 即无论 t 从小于2的一边, 还是从大于2的一边趋近于2时, 平均速度都趋近与一个确定的值 –13.1.
从物理的角度看, 时间间隔 |△t |无限变小时, 平均速度 就无限趋近于 t = 2时的瞬时速度. 因此, 运动员在 t = 2 时的瞬时速度是 –13.1.
表示“当t =2, △t趋近于0时, 平均速度 趋近于确定值– 13.1”.
从2s到(2+△t)s这段时间内平均速度
探
究:
1.运动员在某一时刻 t0 的瞬时速度怎样表示
2.函数f (x)在 x = x0 处的瞬时变化率怎样表示
定义:
函数 y = f (x) 在 x = x0 处的瞬时变化率是
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或 , 即
定义:
函数 y = f (x) 在 x = x0 处的瞬时变化率是
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或 , 即
由导数的定义可知, 求函数 y = f (x)的导数的一般方法:
求函数的改变量
2. 求平均变化率
3. 求值
一差、二化、三极限
题1 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为 f (x) = x2 – 7x+15 ( 0≤x≤8 ) . 计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.
解: 在第2h和第6h时, 原油温度的瞬时变化率就是
和
根据导数的定义,
所以,
同理可得
在第2h和第6h时, 原油温度的瞬时变化率分别为–3和5. 它说明在第2h附近, 原油温度大约以3 / h的速率下降; 在第6h附近,原油温度大约以5 / h的速率上升.
题1 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为 f (x) = x2 – 7x+15 ( 0≤x≤8 ) . 计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.
练习: 计算第3h和第5h时原油的瞬时变化率, 并说明它们的意义.
练习:
课后思考题:
1
2.函数f(x)=|x|在点x0=0处是否有导数?若有,求出来
若没有,请说明理由.
3.1.1 变化率问题
微积分主要与四类问题的处理相关:
一、已知物体运动的路程作为时间的函数,求物体在任意时刻的速度与加速度等;
二、求曲线的切线;
三、求已知函数的最大值与最小值;
四、求长度、面积、体积和重心等。
导数是微积分的核心概念之一,它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具。
问题1 气球膨胀率
在吹气球的过程中, 可发现,随着气球内空气容量的增加, 气球的半径增加得越来越慢. 从数学的角度, 如何描述这种现象呢
气球的体积V(单位:L)与半径r (单位:dm)之间的函数关系是
若将半径 r 表示为体积V的函数, 那么
当空气容量V从0L增加到1L , 气球半径增加了
气球的平均膨胀率为
当空气容量V从1L增加到2 L , 气球半径增加了
气球的平均膨胀率为
随着气球体积逐渐变大,它的平均膨胀率逐渐变小
思考
当空气容量从V1增加到V2时,气球的平均膨胀率是多少
问题2 高台跳水
在高台跳水运动中, 运动员相对于水面的高度 h (单位:m)与起跳后的时间 t (单位:s) 存在函数关系
如果用运动员在某段时间内的平均速度 描述其运动状态, 那么:
在0 ≤ t ≤0.5这段时间里,
在1≤ t ≤2这段时间里,
计算运动员在 这段时间里的平均速度,并思考下面的问题:
探
究:
(1) 运动员在这段时间里是静止的吗
(2) 你认为用平均速度描述运动员的运动状态有什么问题吗
平均速度不能反映他在这段时间里运动状态,
需要用瞬时速度描述运动状态。
定义:
平均变化率:
式子 称为函数 f (x)从x1到 x2的平均变化率.
令△x = x2 – x1 , △ f = f (x2) – f (x1) ,则
理解:
1,式子中△x 、△ f 的值可正、可负,但△x的值不能为0, △ f 的值可以为0
2,若函数f (x)为常函数时, △ f =0
3, 变式
思考
观察函数f(x)的图象
平均变化率
表示什么
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1
f(x2)-f(x1)
直线AB的斜率
练习:
1.甲用5年时间挣到10万元, 乙用5个月时间挣到2万元, 如何比较和评价甲、乙两人的经营成果
2.已知函数 f (x) = 2 x +1, g (x) = – 2 x, 分别计算在下列区间上 f (x) 及 g (x) 的平均变化率.
(1) [ –3 , –1] ; (2) [ 0 , 5 ] .
做两个题吧!
1 、已知函数f(x)=-x2+x的图象上的一点A(-1,-2)及临近一点B(-1+Δx,-2+Δy),则Δy/Δx=( )
A 3 B 3Δx-(Δx)2
C 3-(Δx)2 D 3-Δx
D
2、求y=x2在x=x0附近的平均速度。
2x0+Δx
小结:
1.函数的平均变化率
2.求函数的平均变化率的步骤:
(1)求函数的增量Δf=Δy=f(x2)-f(x1);
(2)计算平均变化率
3.1.2 导数的概念
在高台跳水运动中,平均速度不能反映他在这段时间里运动状态,需要用瞬时速度描述运动状态。我们把物体在某一时刻的速度称为瞬时速度.
又如何求
瞬时速度呢
平均变化率近似地刻画了曲线在某一区间上的变化趋势.
如何精确地刻画曲线在一点处的变化趋势呢
求:从2s到(2+△t)s这段时间内平均速度
△t<0时, 在[ 2+△t, 2 ]这段时
间内 △t>0时, 在[2, 2 +△t ]这段时间内
当△t = – 0.01时,
当△t = 0.01时,
当△t = – 0.001时,
当△t =0.001时,
当△t = –0.0001时,
当△t =0.0001时,
△t = – 0.00001,
△t = 0.00001,
△t = – 0.000001,
△t =0.000001,
……
……
平均变化率近似地刻画了曲线在某一区间上的变化趋势.
如何精确地刻画曲线在一点处的变化趋势呢
当△ t 趋近于0时, 即无论 t 从小于2的一边, 还是从大于2的一边趋近于2时, 平均速度都趋近与一个确定的值 –13.1.
从物理的角度看, 时间间隔 |△t |无限变小时, 平均速度 就无限趋近于 t = 2时的瞬时速度. 因此, 运动员在 t = 2 时的瞬时速度是 –13.1.
表示“当t =2, △t趋近于0时, 平均速度 趋近于确定值– 13.1”.
从2s到(2+△t)s这段时间内平均速度
探
究:
1.运动员在某一时刻 t0 的瞬时速度怎样表示
2.函数f (x)在 x = x0 处的瞬时变化率怎样表示
定义:
函数 y = f (x) 在 x = x0 处的瞬时变化率是
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或 , 即
定义:
函数 y = f (x) 在 x = x0 处的瞬时变化率是
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或 , 即
由导数的定义可知, 求函数 y = f (x)的导数的一般方法:
求函数的改变量
2. 求平均变化率
3. 求值
一差、二化、三极限
题1 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为 f (x) = x2 – 7x+15 ( 0≤x≤8 ) . 计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.
解: 在第2h和第6h时, 原油温度的瞬时变化率就是
和
根据导数的定义,
所以,
同理可得
在第2h和第6h时, 原油温度的瞬时变化率分别为–3和5. 它说明在第2h附近, 原油温度大约以3 / h的速率下降; 在第6h附近,原油温度大约以5 / h的速率上升.
题1 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为 f (x) = x2 – 7x+15 ( 0≤x≤8 ) . 计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.
练习: 计算第3h和第5h时原油的瞬时变化率, 并说明它们的意义.
练习:
课后思考题:
1
2.函数f(x)=|x|在点x0=0处是否有导数?若有,求出来
若没有,请说明理由.
