1.2 矩形的性质与判定 同步练习(含答案解析)
文档属性
| 名称 | 1.2 矩形的性质与判定 同步练习(含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-14 17:18:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学北师大版九年级上学期 第一章 2 矩形的性质与判定
一、单选题
1.下列性质中,矩形不一定具有的是(?? )
A.?对角线相等?????????????B.?对角线互相平分?????????C.?4个内角相等??????????D.?一条对角线平分一组对角
2.在矩形 中, 、 相交于点O,若 的面积为2,则矩形 的面积为(??? )
A.?4????????????????????????????????????B.?6????????????????????????????????????????C.?8??????????????????????????????????????D.?10
3.如图, 在 ABCD中, E为BC的中点, 若四边形AEDF为矩形, 则(??? )
A.?∠B+∠ADE=90°????????????????????B.?DE= AE??????????????????????C.?EF=2AE???????????????????????D.?EF=2AB
4.如图,在一幅矩形风景画外面的四周镶一条金色纸边,制成一幅矩形挂图整个挂图的长80cm,宽50cm如图所示,如果风景画的面积是3500cm2 , 设金色纸边的宽为Xcm,那么X满足的方程是( ??) 【出处:21教育名师】
A.?(80-x)(50-x)=3500????????????????????????????????????????????B.?(80-2x)(50-2x)=3500
C.?(80+x)(50+x)=3500??????????????????????????????????????????D.?(80+2x)(50+2x)=350021*cnjy*com
5.如图,将矩形 折叠,使点C和点A重合,折痕为 , 与 交于点O若 , ,则 的长为(??? )
??????????????????????????????????B.???????????????????????????????????C.??????????????????????????????????D.?
6.如图,将矩形ABCD沿AC折叠,使点B落在点B′处,B′C交AD于点E,若∠l=25°,则∠2等于(?? )
A.?25°???????????????????????????????B.?30°?????????????????????????C.?50°????????????????????????????????D.?60°
二、填空题
7.如图在平行四边形ABCD中,添加一个条件________,可得平行四边形ABCD是矩形。
8.如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF,点F在矩形ABCD的内部,将BF延长交AD于点G.若 = ,则 =________.
9.如图,点 是矩形 的对角线 上一点,过点 作 交 于 ,交 于 ,若 , ,则图中阴影部分的面积为________. 2·1·c·n·j·y
10.已知一个矩形的对角线的长为4,它们的夹角是60°,则这个矩形的较短的边长为________,面积为 ________.
11.如图,在 中, , , ,点E为边AB上的一个动点,连接ED并延长至点F,使得 ,以EC、EF为邻边构造 ,连接EG,则EG的最小值为________.
三、综合题
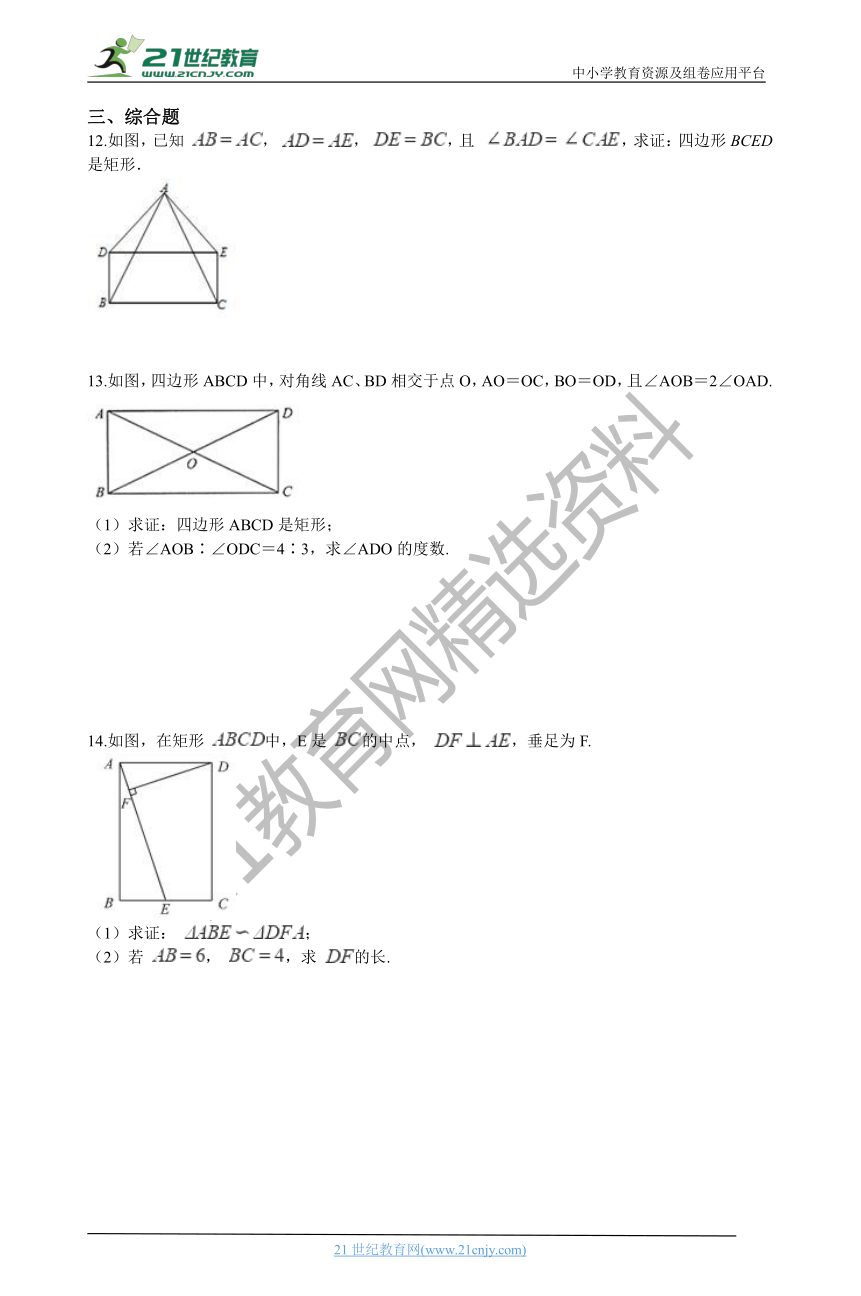
12.如图,已知 , , ,且 ,求证:四边形BCED是矩形.
13.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
14.如图,在矩形 中,E是 的中点, ,垂足为F.
(1)求证: ;
(2)若 , ,求 的长.
15.如图,四边形 是矩形,E是 边上一点,点F在 的延长线上,且 .
(1)求证:四边形 是平行四边形;
(2)连接 ,若 , , ,求四边形 的面积.
答案解析部分
一、单选题
1. D
解析:B是一般的平行四边形的性质,A、C都是矩形特有的性质,D是菱形的性质,矩形不一定具有; 21世纪教育网版权所有
故答案为:D.
【分析】本题主要应用矩形的性质,即对角线相等且互相平分,四个角都是直角,对边平行且相等,进行解答即可.21·cn·jy·com
2. C
解析:∵四边形ABCD是矩形,对角线 、 相交于点O,
∴AC=BD,且OA=OB=OC=OD,
∴ ,
∴矩形 的面积为 ,
故答案为:C.
【分析】根据矩形的性质得到OA=OB=OC=OD,推出 ,即可求出矩形ABCD的面积.
3. D
解析:设矩形AEDF的对角线的交点为O,
∴AO=AD,EF=2OE,
∵E为BC的中点,
∴BE=BC
∵平行四边形ABCD
∴AD=BC,AO∥BE,
∴AO=BE,
∴四边形AOEB是平行四边形,
∴AB=OE
∴EF=2AB.
故答案为:D. www.21-cn-jy.com
【分析】利用矩形的性质,可知AO=AD,EF=2OE,再利用线段中点的定义及平行四边形的性质,可以推出AO=BE,AO∥BE,由此可证得四边形AOEB是平行四边形,根据平行四边形的对边相等,可得到AB=OE,即可证得结论。21·世纪*教育网
4. B
解析:根据题意可知,风景画的长为(80-2x)cm,宽为(50-2x)cm
∴风景画的面积可表示为(80-2x)(50-2x)=3500 【来源:21cnj*y.co*m】
故答案为:B。
【分析】根据题意,分别表示出矩形风景画的长和宽,根据矩形的面积公式计算得到其面积等于3500,即可得到方程。
5. C
解析:由对折可得:
?矩形 ,
?
?
?
?
BC=8
?
由对折得:
故答案为:C.
【分析】先证明 再求解 利用轴对称可得答案.
6. C
解析:由折叠的性质可知:∠ACB′=∠1=25°.
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠2=∠1+∠ACB′=25°+25°=50°.
故答案为:C.
【分析】 由折叠的性质可得∠ACB′=∠1,由矩形的性质可得出AD∥BC,再根据“两直线平行,内错角相等”可求出∠2的度数.21教育网
二、填空题
7. AC=BD(答案不唯一)
解析:添加条件为AC=BD,
∵四边形ABCD为平行四边形,AC=BD
∴平行四边形ABCD为矩形 【来源:21·世纪·教育·网】
【分析】根据矩形的判定定理,添加合适的条件即可得到答案。
8.
解析:如图,连接GE,
∵点E是CD的中点,
∴DE=EC,
∵将△BCE沿BE折叠后得到△BEF,点F在矩形ABCD的内部,
∴∠BFE=90°,EF=EC=ED,
在Rt△EFG和△EDG中,
,
∴Rt△EFG≌△EDG(HL),
∴FG=DG,
∵,
设DG=FG=x,则AG=7x,AD=BC=8x,BG=BF+FG=9x,
∴,
∴.
故答案为:.
【分析】连接GE,易证Rt△EFG≌△EDG,设DG=FG=x,则AG=7x,AD=BC=8x,BG=BF+FG=9x,表示出, 进而得到.
9. 5
解析:作GM⊥AB于M,延长MG交CD于N.
则有四边形AEGM,四边形DEGN,四边形CFGN,四边形BMGF都是矩形,
∴AE=BF=2,S△ADB=S△DBC , S△BGM=S△BGF , S△DEG=S△DNG ,
∴S矩形AEGM=S矩形CFGN=2×5=10,
∴S阴= S矩形CFGN=5,
故答案为:5.
【分析】由矩形的性质可证明S矩形AEGM=S矩形CFGN=2×5=10,即可求解.
10. 2;4
解析:
∵矩形的对角线的夹角是60°
∴较短的边对的三角形是等边三角形
∴这个矩形的较短的边长为2
∴这个矩形较长的边
∴这个矩形的面积
故答案为:2;.
【分析】根据矩形的性质结合对角线的夹角是60°可得较短的边对的三角形是等边三角形,再根据等边三角形的性质结合勾股定理即可求得矩形较长的边,从而求得矩形的面积.
11. 9
解析:连接FC,交EG于点O,过点D作DM//FC,交EG于点M,如图所示,
∵
∴
∵DM//FC,
∴△DEM∽△FEO,
∴ ,
∵DM//FC,
∴△DMN∽△CON,
∴ ,
∵四边形ECGF是平行四边形,
∴CO=FO,
∴
∴ ,
∴ ,
过点C作CH⊥AB于点H,
在Rt△CBH,∠B=60?,BC=8,
∴CH=BCsin60?=4 ,
根据题意得,EG必过点N,当EN⊥CD时,EG最小,此时四边形EHCN是矩形,
∴EN=CH=4 ,
∴EO= ,
∴EG=2EO=9 .
?故答案为:9 .
【分析】连接FC,作DM//FC,得△DEM∽△FEO,△DMN∽△CON,进一步得出DM= ,EO= ,过C作CH⊥AB于H,可求出CH= ,根据题意,EG必过点N,当EN⊥CD时,EG最小,此时四边形EHCN是矩形,故可得EN=CH= ,代入EO= 求出EO即可得到结论.21cnjy.com
三、综合题
12. 证明:连接BE、CD.
在△ABD和△ACE中
∵AB=AC,AD=AE,∠BAD=∠CAE
∴△ABD≌△ACE(SAS)
∴BD=CE
∵DE=BC
∴四边形BCED为平行四边形
∵∠BAD=∠CAE
∴∠BAD+∠CAB=∠CAE+∠CAB
即∠CAD=∠BAE
在△ACD和△ABE中,
∵AC=AB,AD=AE,∠CAD=∠BAE
∴△ADC≌△AEB(SAS)
∴CD=BE
∴四边形BCED为矩形。 www-2-1-cnjy-com
解析:先利用已知条件证出△ABD≌△ACE,从而得BD=CE,加上DE=BC,可证地四边形BCED为平行四边形;然后再证得△ADC≌△AEB,从而得CD=BE,故利用矩形的判定方法得证。2-1-c-n-j-y
13. (1)证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形,
又∵∠AOB=2∠OAD,∠AOB是△AOD的外角,
∴∠AOB=∠OAD+∠ADO.
∴∠OAD=∠ADO.
∴AO=OD.
?又∵AC=AO+OC=2AO,BD=BO+OD=2OD,
∴AC=BD.
∴四边形ABCD是矩形.
(2)证明:设∠AOB=4x,∠ODC=3x,则∠ODC=∠OCD=3x,
在△ODC中,∠DOC+∠OCD+∠CDO=180°
∴4x+3x+3x=180°,解得x=18°,
∴∠ODC=3×18°=54°,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADO=∠ADC-∠ODC=90°-54°=36°.
解析:(1)首先根据对角线互相平分的四边形是平行四边形由 AO=OC,BO=OD, 得出四边形ABCD是平行四边形, 根据三角形外角定理及 ∠AOB=2∠OAD 得出 ∠OAD=∠ADO,根据等角对等边得出 AO=OD ,进而即可推出 AC=BD ,根据对角线相等的平行四边形是矩形得出结论: 四边形ABCD是矩形 ;
(2) 设∠AOB=4x,∠ODC=3x,则∠ODC=∠OCD=3x, 根据三角形的内角和及对顶角相等列出方程,求解算出x的值,从而∠ ODC ,再根据矩形的四个角都是直角及角的和差即可算出答案。
14. (1)证明:∵四边形 是矩形,
∴ , .
∴ ,
∵ ,
∴ .
∴ ,
∴ .
(2)解:∵ ,
∴ .
∵ , 是 的中点,
∴ .
∴在 中, .
又∵ ,
∴ ,
∴ .
解析:(1)根据矩形的性质可得, , .再根据“两直线平行,内错角相等”可得 ,再由垂直的定义可得 .从而得出 ,再根据“有两组角对应相等的两个三角形相似”可得出结论;
(2)根据中点的定义可求出BE=2,然后根据勾股定理求出AE= .再根据相似三角形的性质求解即可.【版权所有:21教育】
15. (1)证明:∵四边形 是矩形,
∴ , .
∵ ,
∴ ,即 .
∴ ,
∴四边形 是平行四边形.
(2)解:如图,连接 ,
∵四边形 是矩形
∴
在 中, , ,
∴由勾股定理得, ,即 .
∵ ,
∴ .
∵ ,
∴ .
∴ 即 ,解得 .
由(1)得四边形 是平行四边形,
又∵ ,高 ,
∴ .
解析:(1)直接利用矩形的性质结合BE=CF,可得 ,进而得出答案;(2)在 中利用勾股定理可计算 ,再由求出 得 ,进而求出AD长,由 即可求解.21教育名师原创作品
_21?????????è?????(www.21cnjy.com)_
初中数学北师大版九年级上学期 第一章 2 矩形的性质与判定
一、单选题
1.下列性质中,矩形不一定具有的是(?? )
A.?对角线相等?????????????B.?对角线互相平分?????????C.?4个内角相等??????????D.?一条对角线平分一组对角
2.在矩形 中, 、 相交于点O,若 的面积为2,则矩形 的面积为(??? )
A.?4????????????????????????????????????B.?6????????????????????????????????????????C.?8??????????????????????????????????????D.?10
3.如图, 在 ABCD中, E为BC的中点, 若四边形AEDF为矩形, 则(??? )
A.?∠B+∠ADE=90°????????????????????B.?DE= AE??????????????????????C.?EF=2AE???????????????????????D.?EF=2AB
4.如图,在一幅矩形风景画外面的四周镶一条金色纸边,制成一幅矩形挂图整个挂图的长80cm,宽50cm如图所示,如果风景画的面积是3500cm2 , 设金色纸边的宽为Xcm,那么X满足的方程是( ??) 【出处:21教育名师】
A.?(80-x)(50-x)=3500????????????????????????????????????????????B.?(80-2x)(50-2x)=3500
C.?(80+x)(50+x)=3500??????????????????????????????????????????D.?(80+2x)(50+2x)=350021*cnjy*com
5.如图,将矩形 折叠,使点C和点A重合,折痕为 , 与 交于点O若 , ,则 的长为(??? )
??????????????????????????????????B.???????????????????????????????????C.??????????????????????????????????D.?
6.如图,将矩形ABCD沿AC折叠,使点B落在点B′处,B′C交AD于点E,若∠l=25°,则∠2等于(?? )
A.?25°???????????????????????????????B.?30°?????????????????????????C.?50°????????????????????????????????D.?60°
二、填空题
7.如图在平行四边形ABCD中,添加一个条件________,可得平行四边形ABCD是矩形。
8.如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF,点F在矩形ABCD的内部,将BF延长交AD于点G.若 = ,则 =________.
9.如图,点 是矩形 的对角线 上一点,过点 作 交 于 ,交 于 ,若 , ,则图中阴影部分的面积为________. 2·1·c·n·j·y
10.已知一个矩形的对角线的长为4,它们的夹角是60°,则这个矩形的较短的边长为________,面积为 ________.
11.如图,在 中, , , ,点E为边AB上的一个动点,连接ED并延长至点F,使得 ,以EC、EF为邻边构造 ,连接EG,则EG的最小值为________.
三、综合题
12.如图,已知 , , ,且 ,求证:四边形BCED是矩形.
13.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
14.如图,在矩形 中,E是 的中点, ,垂足为F.
(1)求证: ;
(2)若 , ,求 的长.
15.如图,四边形 是矩形,E是 边上一点,点F在 的延长线上,且 .
(1)求证:四边形 是平行四边形;
(2)连接 ,若 , , ,求四边形 的面积.
答案解析部分
一、单选题
1. D
解析:B是一般的平行四边形的性质,A、C都是矩形特有的性质,D是菱形的性质,矩形不一定具有; 21世纪教育网版权所有
故答案为:D.
【分析】本题主要应用矩形的性质,即对角线相等且互相平分,四个角都是直角,对边平行且相等,进行解答即可.21·cn·jy·com
2. C
解析:∵四边形ABCD是矩形,对角线 、 相交于点O,
∴AC=BD,且OA=OB=OC=OD,
∴ ,
∴矩形 的面积为 ,
故答案为:C.
【分析】根据矩形的性质得到OA=OB=OC=OD,推出 ,即可求出矩形ABCD的面积.
3. D
解析:设矩形AEDF的对角线的交点为O,
∴AO=AD,EF=2OE,
∵E为BC的中点,
∴BE=BC
∵平行四边形ABCD
∴AD=BC,AO∥BE,
∴AO=BE,
∴四边形AOEB是平行四边形,
∴AB=OE
∴EF=2AB.
故答案为:D. www.21-cn-jy.com
【分析】利用矩形的性质,可知AO=AD,EF=2OE,再利用线段中点的定义及平行四边形的性质,可以推出AO=BE,AO∥BE,由此可证得四边形AOEB是平行四边形,根据平行四边形的对边相等,可得到AB=OE,即可证得结论。21·世纪*教育网
4. B
解析:根据题意可知,风景画的长为(80-2x)cm,宽为(50-2x)cm
∴风景画的面积可表示为(80-2x)(50-2x)=3500 【来源:21cnj*y.co*m】
故答案为:B。
【分析】根据题意,分别表示出矩形风景画的长和宽,根据矩形的面积公式计算得到其面积等于3500,即可得到方程。
5. C
解析:由对折可得:
?矩形 ,
?
?
?
?
BC=8
?
由对折得:
故答案为:C.
【分析】先证明 再求解 利用轴对称可得答案.
6. C
解析:由折叠的性质可知:∠ACB′=∠1=25°.
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠2=∠1+∠ACB′=25°+25°=50°.
故答案为:C.
【分析】 由折叠的性质可得∠ACB′=∠1,由矩形的性质可得出AD∥BC,再根据“两直线平行,内错角相等”可求出∠2的度数.21教育网
二、填空题
7. AC=BD(答案不唯一)
解析:添加条件为AC=BD,
∵四边形ABCD为平行四边形,AC=BD
∴平行四边形ABCD为矩形 【来源:21·世纪·教育·网】
【分析】根据矩形的判定定理,添加合适的条件即可得到答案。
8.
解析:如图,连接GE,
∵点E是CD的中点,
∴DE=EC,
∵将△BCE沿BE折叠后得到△BEF,点F在矩形ABCD的内部,
∴∠BFE=90°,EF=EC=ED,
在Rt△EFG和△EDG中,
,
∴Rt△EFG≌△EDG(HL),
∴FG=DG,
∵,
设DG=FG=x,则AG=7x,AD=BC=8x,BG=BF+FG=9x,
∴,
∴.
故答案为:.
【分析】连接GE,易证Rt△EFG≌△EDG,设DG=FG=x,则AG=7x,AD=BC=8x,BG=BF+FG=9x,表示出, 进而得到.
9. 5
解析:作GM⊥AB于M,延长MG交CD于N.
则有四边形AEGM,四边形DEGN,四边形CFGN,四边形BMGF都是矩形,
∴AE=BF=2,S△ADB=S△DBC , S△BGM=S△BGF , S△DEG=S△DNG ,
∴S矩形AEGM=S矩形CFGN=2×5=10,
∴S阴= S矩形CFGN=5,
故答案为:5.
【分析】由矩形的性质可证明S矩形AEGM=S矩形CFGN=2×5=10,即可求解.
10. 2;4
解析:
∵矩形的对角线的夹角是60°
∴较短的边对的三角形是等边三角形
∴这个矩形的较短的边长为2
∴这个矩形较长的边
∴这个矩形的面积
故答案为:2;.
【分析】根据矩形的性质结合对角线的夹角是60°可得较短的边对的三角形是等边三角形,再根据等边三角形的性质结合勾股定理即可求得矩形较长的边,从而求得矩形的面积.
11. 9
解析:连接FC,交EG于点O,过点D作DM//FC,交EG于点M,如图所示,
∵
∴
∵DM//FC,
∴△DEM∽△FEO,
∴ ,
∵DM//FC,
∴△DMN∽△CON,
∴ ,
∵四边形ECGF是平行四边形,
∴CO=FO,
∴
∴ ,
∴ ,
过点C作CH⊥AB于点H,
在Rt△CBH,∠B=60?,BC=8,
∴CH=BCsin60?=4 ,
根据题意得,EG必过点N,当EN⊥CD时,EG最小,此时四边形EHCN是矩形,
∴EN=CH=4 ,
∴EO= ,
∴EG=2EO=9 .
?故答案为:9 .
【分析】连接FC,作DM//FC,得△DEM∽△FEO,△DMN∽△CON,进一步得出DM= ,EO= ,过C作CH⊥AB于H,可求出CH= ,根据题意,EG必过点N,当EN⊥CD时,EG最小,此时四边形EHCN是矩形,故可得EN=CH= ,代入EO= 求出EO即可得到结论.21cnjy.com
三、综合题
12. 证明:连接BE、CD.
在△ABD和△ACE中
∵AB=AC,AD=AE,∠BAD=∠CAE
∴△ABD≌△ACE(SAS)
∴BD=CE
∵DE=BC
∴四边形BCED为平行四边形
∵∠BAD=∠CAE
∴∠BAD+∠CAB=∠CAE+∠CAB
即∠CAD=∠BAE
在△ACD和△ABE中,
∵AC=AB,AD=AE,∠CAD=∠BAE
∴△ADC≌△AEB(SAS)
∴CD=BE
∴四边形BCED为矩形。 www-2-1-cnjy-com
解析:先利用已知条件证出△ABD≌△ACE,从而得BD=CE,加上DE=BC,可证地四边形BCED为平行四边形;然后再证得△ADC≌△AEB,从而得CD=BE,故利用矩形的判定方法得证。2-1-c-n-j-y
13. (1)证明:∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形,
又∵∠AOB=2∠OAD,∠AOB是△AOD的外角,
∴∠AOB=∠OAD+∠ADO.
∴∠OAD=∠ADO.
∴AO=OD.
?又∵AC=AO+OC=2AO,BD=BO+OD=2OD,
∴AC=BD.
∴四边形ABCD是矩形.
(2)证明:设∠AOB=4x,∠ODC=3x,则∠ODC=∠OCD=3x,
在△ODC中,∠DOC+∠OCD+∠CDO=180°
∴4x+3x+3x=180°,解得x=18°,
∴∠ODC=3×18°=54°,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADO=∠ADC-∠ODC=90°-54°=36°.
解析:(1)首先根据对角线互相平分的四边形是平行四边形由 AO=OC,BO=OD, 得出四边形ABCD是平行四边形, 根据三角形外角定理及 ∠AOB=2∠OAD 得出 ∠OAD=∠ADO,根据等角对等边得出 AO=OD ,进而即可推出 AC=BD ,根据对角线相等的平行四边形是矩形得出结论: 四边形ABCD是矩形 ;
(2) 设∠AOB=4x,∠ODC=3x,则∠ODC=∠OCD=3x, 根据三角形的内角和及对顶角相等列出方程,求解算出x的值,从而∠ ODC ,再根据矩形的四个角都是直角及角的和差即可算出答案。
14. (1)证明:∵四边形 是矩形,
∴ , .
∴ ,
∵ ,
∴ .
∴ ,
∴ .
(2)解:∵ ,
∴ .
∵ , 是 的中点,
∴ .
∴在 中, .
又∵ ,
∴ ,
∴ .
解析:(1)根据矩形的性质可得, , .再根据“两直线平行,内错角相等”可得 ,再由垂直的定义可得 .从而得出 ,再根据“有两组角对应相等的两个三角形相似”可得出结论;
(2)根据中点的定义可求出BE=2,然后根据勾股定理求出AE= .再根据相似三角形的性质求解即可.【版权所有:21教育】
15. (1)证明:∵四边形 是矩形,
∴ , .
∵ ,
∴ ,即 .
∴ ,
∴四边形 是平行四边形.
(2)解:如图,连接 ,
∵四边形 是矩形
∴
在 中, , ,
∴由勾股定理得, ,即 .
∵ ,
∴ .
∵ ,
∴ .
∴ 即 ,解得 .
由(1)得四边形 是平行四边形,
又∵ ,高 ,
∴ .
解析:(1)直接利用矩形的性质结合BE=CF,可得 ,进而得出答案;(2)在 中利用勾股定理可计算 ,再由求出 得 ,进而求出AD长,由 即可求解.21教育名师原创作品
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
