北师大版八年级上册第一章勾股定理 专题复习教案
文档属性
| 名称 | 北师大版八年级上册第一章勾股定理 专题复习教案 |  | |
| 格式 | zip | ||
| 文件大小 | 690.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-14 21:42:03 | ||
图片预览



文档简介
第一章《勾股定理》专项练习
专题一:勾股定理
考点分析:
勾股定理单独命题的题目较少,常与方程、函数,四边形等知识综合在一起考查,在中考试卷中的常见题型为填空题、选择题和较简单的解答题
典例剖析
例1.(1)如图1是一个外轮廓为矩形的机器零件
平面示意图,根据图中的尺寸(单位:),计算
两圆孔中心和的距离为______.
(2)如图2,直线上有三个正方形,若
的面积分别为5和11,则的面积为( )
A.4
B.6
C.16
D.55
分析:本题结合图中的尺寸直接运用勾股定理计算即可.
解:(1)由已知得:AC=150-60=90,BC=180-60=120,由勾股定理得:
AB2=902+1202=22500,所以AB=150(mm)
(2)由勾股定理得:b=a+c=5+11=16,故选C.
点评:以上两例都是勾股定理的直接运用,当已知直角三角形的两边,求第三边时,往往要借助于勾股定理来解决.
例2.如图3,正方形网格的每一个小正方形的边长都是1,试求的度数.
解:连.,,
(SAS).
.
由勾股定理,得:,,
,(SSS).
.
由图可知为等腰直角三角形..
即.
点评:由于在正方形网格中,它有两个主要特征:(1)任何格点之间的线段都是某正方形或长方形的边或对角线,所以格点间的任何线段长度都能求得.
(2)利用正方形的性质,我们很容易知道一些特殊的角,如450、900、1350,便一目了然.以上两例就是根据网格的直观性,再结合图形特点,运用勾股定理进行计算,易求得线段和角的特殊值,重点考查学生的直觉观察能力和数形结合的能力.
专练一:
1、△ABC中,∠A:∠B:∠C=2:1:1,a,b,c分别是∠A、∠B、∠C的对边,则下列各等式中成立的是(
)
(A);(B);
(C);
(D)
2、若直角三角形的三边长分别为2,4,x,则x的可能值有(
)
(A)1个;
(B)2个;
(C)3个;
(D)4个
3、一根旗杆在离底面4.5米的地方折断,旗杆顶端落在离旗杆底部6米处,则旗杆折断前高为(
)
(A)10.5米;
(B)7.5米;
(C)12米;
(D)8米
4、下列说法中正确的有(
)
(1)如果∠A+∠B+∠C=3:4:5,则△ABC是直角三角形;(2)如果∠A+∠B=∠C,那么△ABC是直角三角形;(3)如果三角形三边之比为6:8:10,则ABC是直角三角形;(4)如果三边长分别是,则ABC是直角三角形。
(A)1个;
(B)2个;
(C)3个;
(D)4个
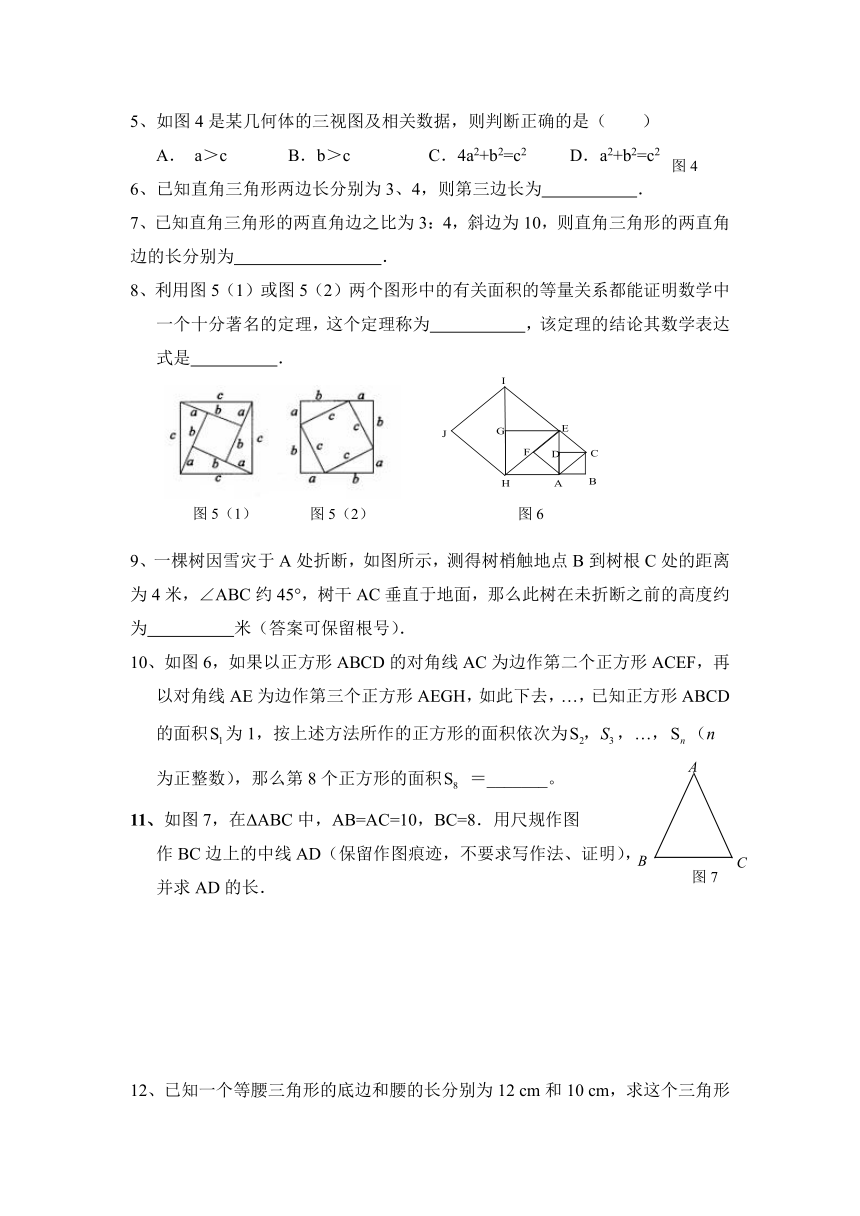
5、如图4是某几何体的三视图及相关数据,则判断正确的是(
)
A.
a>c
B.b>c
C.4a2+b2=c2
D.a2+b2=c2
6、已知直角三角形两边长分别为3、4,则第三边长为
.
7、已知直角三角形的两直角边之比为3:4,斜边为10,则直角三角形的两直角边的长分别为
.
8、利用图5(1)或图5(2)两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为
,该定理的结论其数学表达式是
.
9、一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为
米(答案可保留根号).
10、如图6,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积为1,按上述方法所作的正方形的面积依次为,…,(n为正整数),那么第8个正方形的面积
=_______。
11、如图7,在ΔABC中,AB=AC=10,BC=8.用尺规作图
作BC边上的中线AD(保留作图痕迹,不要求写作法、证明),
并求AD的长.
12、已知一个等腰三角形的底边和腰的长分别为12
cm和10
cm,求这个三角形的面积.
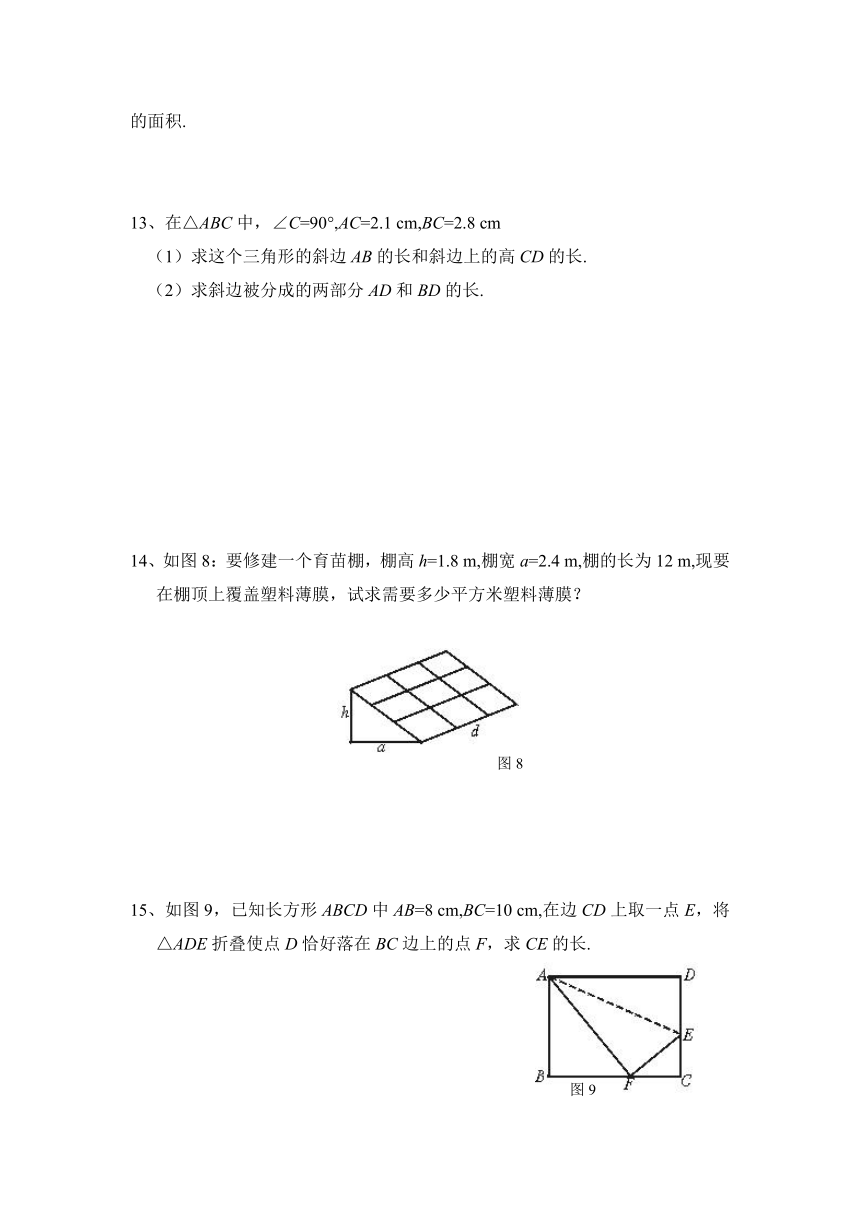
13、在△ABC中,∠C=90°,AC=2.1
cm,BC=2.8
cm
(1)求这个三角形的斜边AB的长和斜边上的高CD的长.
(2)求斜边被分成的两部分AD和BD的长.
14、如图8:要修建一个育苗棚,棚高h=1.8
m,棚宽a=2.4
m,棚的长为12
m,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
15、如图9,已知长方形ABCD中AB=8
cm,BC=10
cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
专题二:一定是直角三角形吗
考点分析:
本部分内容是勾股定理及其逆定理的应用,它在中考试卷中不单独命题,常与其它知识综合命题
典例剖析
例1.如图10,A、B两点都与平面镜相距4米,且A、B两点相距6米,一束光线由A射向平面镜反射之后恰巧经过B点,求B点到入射点的距离.
分析:此题要用到勾股定理,全等三角形,轴对称及物理上的光的反射的知识.
解:作出B点关于CD的对称点B′,连结AB′,交CD于点O,则O点就是光的入射点,因为B′D=DB,所以B′D=AC,∠B′DO=∠OCA=90°,∠B′=∠CAO
所以△B′DO≌△ACO(SSS),则OC=OD=AB=×6=3米,连结OB,在Rt△ODB中,OD2+BD2=OB2,所以OB2=32+42=52,即OB=5(米),所以点B到入射点的距离为5米.
评注:这是以光的反射为背景的一道综合题,涉及到许多几何知识,由此可见,数学是学习物理的基础
例2.如果只给你一把带刻度的直尺,你是否能检验∠MPN是不是直角,简述你的作法.
分析:只有一把刻度尺,只能用这把刻度尺量取线段的长度,若∠P是一个直角,∠P所在的三角形必是个直角三角形,这就提示我们把∠P放在一个三角形中,利用勾股定理的逆定理来解决此题.
作法:①在射线PM上量取PA=3㎝,确定A点,
在射线PN上量取PB=4㎝,确定B点.
②连结AB得△PAB.
③用刻度尺量取AB的长度,
如果AB恰为5㎝,则说明∠P是直角,否则∠P不是直角.
理由:PA=3㎝,PB=4㎝,PA+PB=3+4=5,
若AB=5㎝,则PA+PB=AB,根据勾股定理的逆定理得△PAB是直角三角形,∠P是直角.
说明:这是一道动手操作题,是勾股定理的逆定理在现实生活中的一个典型应用.学生既要会动手操作,又必须能够把操作的步骤完整的表述出来,同时要清楚每个操作题的理论基础.
专练二:
1.做一做:作一个三角形,使三边长分别为3
cm,4
cm,5
cm,哪条边所对的角是直角?为什么?
2.断一断:设三角形的三边分别等于下列各组数:
①7,8,10
②7,24,25
③12,35,37
④13,11,10
(1)请判断哪组数所代表的三角形是直角三角形,为什么?
(2)把你判断是Rt△的哪组数作出它所表示的三角形,并用量角器来进行验证.
3.算一算:.一个零件的形状如图12,已知AC=3㎝,AB=4㎝,BD=12㎝,
求:CD的长.
4.一个零件的形状如图13所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
5.如图14,等边三角形ABC内一点P,AP=3,BP=4,CP=5,求∠APB的度数.
6.若△ABC的三边长为a,b,c,根据下列条件判断△ABC的形状.
(1)a2+b2+c2+200=12a+16b+20c
(2)a3-a2b+ab2-ac2+bc2-b3=0
7.请在由边长为1的小正三角形组成的虚线网格中,画出1
个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形.
8.为筹备迎新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图15,已知圆筒高108㎝,其截面周长为36㎝,如果在表面缠绕油纸4圈,应裁剪多长油纸.
专题三:勾股定理的应用
考点分析:
勾股定理在实际生活中的应用较为广泛,它常常单独命题,有时也与方程、函数,四边形等知识综合在一起考查,在中考试卷中的常见题型为填空题、选择题和较简单的解答题
典例剖析
例1.如图16(1)所示,一个梯子AB长2.5米,
顶端A靠在墙AC上,这时梯子下端B与墙角C距离
为1.5米,梯子滑动后停在DE位置上,如图10(2)所示,
测得得BD=0.5米,求梯子顶端A下落了多少米?
分析:梯子顶端A下落的距离为AE,
即求AE的长.已知AB和BC,根据勾股定理可求AC,
只要求出EC即可。
解:在Rt△ACB中,AC2=AB2-BC2=2.52-1.52=4,
∴AC=2,∵BD=0.5,∴CD=2
∴EC=1.5,
,所以,梯子顶端下滑了0.5米.
点评:在实际生活、生产及建筑中,当人们自身高度达不到时,往往要借助于梯子,这时对梯子的选择,及梯子所能达到的高度等问题,往往要用到勾股定理的知识来解决.但要
注意:考虑梯子的长度不变.
例2.有一根竹竿,
不知道它有多长.
把竹竿横放在一扇门前,
竹竿长比门宽多4尺;把竹竿竖放在这扇门前,
竹竿长比门的高度多2尺;
把竹竿斜放,,竹竿长正好和门的对角线等长.问竹竿长几尺?
分析:只要根据题意,画出图形,然后利用勾股定理,列出方程解之
解:设竹竿长为x尺。则:(x―4)2+(x―2)2=x2
x1=10
,x2=2(不合题意舍去)
答:竹竿长为10尺。
评注:本题是勾股定理与方程的综合应用问题,它综合考查了同学们的建模思想和方法的理解和运用,符合新课程标准的理念,请注意这类问题!
例3.如图17,客轮在海上以30km/h的速度由向航行,在处测得灯塔的方位角为北偏东,测得处的方位角为南偏东,航行1小时后到达处,在处测得的方位角为北偏东,则到的距离是(
)
A.km;B.km;C.km;D.km
分析:本题是一道以航海为背景的应用题,由已知条件分析易知△ABC
不是直角三角形,这就需要作三角形的高,将非直角三角形转化为直角三角形,
问题便可得到解决.
解:由条件易得:∠C=450,∠ABC=750,则∠A=600,过B作BD⊥AC,
垂足为D,∴△BCD是等腰直角三角形,又∵BC=30km,由勾股定理得:
2CD2=302,∴CD=,∴BD=,设AD=x,则AB=2x,由勾股定理得:BD=,∴=,∴x=,∴AC=+,故选D.
点评:
在航海中,有时需要求两船或船与某地方的距离,以保证航海的安全,有时就需要用勾股定理及判定条件来加以解决,熟练应用勾股定理是解题的关键.
专练三:
1.小明从家走到邮局用了8分钟,然后右转弯用同样的速度走了6分钟到达书店(如图18),已知书店距离邮局640米,那么小明家距离书店
米.
2.一根新生的芦苇高出水面1尺,一阵风吹过,芦苇被吹倒一边,顶端齐至水面,芦苇移动的水平距离为5尺,则水池的深度和芦苇的长度各是
.
3.小明叔叔家承包了一个矩形养鱼池,已知其面积为48m,其对角线长为10m,为建起栅栏,要计算这个矩形养鱼池的周长,你能帮助小明算一算,周长应该是
.
4.求图19所示(单位mm)矩形零件上两孔
中心A和B的距离(精确到0.lmm).
5.假期,小王与同学们在公园里探宝玩游戏,按照游戏中提示的方向,他们从A出发先向正东走了800米,再向正北走了200米,折向正西走300米,再向正北走600米,再向正东走100米,到达了宝藏处B,问A、B间的直线距离是
米.
6.如图20所示,为修铁路需凿通隧道AC,测得∠A=53°,
∠B=37°.AB=5km,BC=4km,若每天凿0.3km,
试计算需要几天才能把隧道AC凿通.
7.如图21,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
8.观察下列表格:
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
……
……
13、b、c
132=b+c
请你结合该表格及相关知识,求出b、c的值。
9.如图22所示的一块地,AD=12m,CD=9m,∠ADC=90°,AB=39m,BC=36m,求这块地的面积.
参考答案
专练一:
1.;2.12,13;
3.28;
5、1000
6.
解:因为∠A=53°,∠B=37°∴∠ACB=90°,
在Rt△ABC中,AC=AB-BC=5-4=9,所以AC=3,需要的时间
(天)
答:需要10天才能把隧道AC凿通。
7.由勾股定理得:AB=10,设CD=x,则DE=x,BD=8-x,BE=4,由勾股定理得:
42+x2=(8-x)2,解得x=3,即CD=3
8.12,5
9.连结AC,在Rt△ADC中,
,
,在△ABC中,AB2=1521
,
答:这块地的面积是216平方米。
专练二:
1.做一做:5
cm所对的角是直角,因为在直角三角形中直角所对边最长.
2.断一断:(1)②③
∵72+242=252,
122+352=372
(2)略
3.解:在直角三角形ABC中,根据勾股定理:BC=AC+AB=3+4=25,在直角三角形CBD中,根据勾股定理:CD=BC+BD=25+12=169,∴CD=13.
4.∵42+32=52,52+122=132,即AB2+BC2=AC2,故∠B=90°,同理,∠ACD=90°
∴S四边形ABCD=S△ABC+S△ACD=×3×4+×5×12=6+30=36.
5.解:如图,以AP为边作等边△APD,连结BD.则∠1=60°-∠BAP=
∠2,
在△ADB和△APC中,
AD=AP.∠1=∠2,AB=AC
∴△ADB≌△ADC(SAS)
∴BD=PC=5,又PD=AP=3,BP=4
∴BP2+PD2=42+32=25=BD2
∴∠BPD=90°
∴∠APB=∠APD+∠BPD=150°
6.(1)∵a2+b2+c2+100=12a+16b+20c,∴(a2-12a+36)+(b2-16b+64)+(c2-20c+100)=0,
即(a-6)2+(b-8)2+(c-10)2=0
∴a-6=0,b-8=0,c-10=0,即a=6,b=8,c=10,而62+82=100=102,∴a2+b2=c2,
∴△ABC为直角三角形.
(2)(a3-a2b)+(ab2-b3)-(ac2-bc2)=0,a2(a-b)+b2(a-b)-c2(a-b)=0,∴(a-b)(a2+b2-c2)=0
∴a-b=0或a2+b2-c2=0,∴此三角形ABC为等腰三角形或直角三角形.
7.解:本题答案不惟一,只要符合要求都可以,以下答案供参考.
8.解:将圆筒展开后成为一个矩形,如图,
整个油纸也随之分成相等4段只需求出AC长
即可,在Rt△ABC中,AB=36,BC=
∴由勾股定理得AC=AB+BC=36+27
∴AC=45,故整个油纸的长为45×4=180(㎝).
专练三:
1、C;2、B;3、B;4、C;5、D;6、5,;7、6,8;8、勾股定理,;9、;10、128;
11、(1)作图略;
(2)在△ABC中,AB=AC,AD是△ABC的中线,∴AD⊥BC,.在Rt△ABD中,AB=10,BD=4,,
.
12、如图:等边△ABC中BC=12
cm,AB=AC=10
cm
作AD⊥BC,垂足为D,则D为BC中点,BD=CD=6
cm,在Rt△ABD中,AD2=AB2-BD2=102-62=64
∴AD=8
cm
∴S△ABD=BC·AD=×12×8=48(cm2)
13、解:(1)∵△ABC中,∠C=90°,AC=2.1
cm,BC=2.8
cm
∴AB2=AC2+BC2=2.12+2.82=12.25
∴AB=3.5
cm,∵S△ABC=AC·BC=AB·CD,∴AC·BC=AB·CD,
∴CD===1.68(cm)
(2)在Rt△ACD中,由勾股定理得:AD2+CD2=AC2,
∴AD2=AC2-CD2=2.12-1.682=(2.1+1.68)(2.1-1.68)
=3.78×0.42=2×1.89×2×0.21=22×9×0.21×0.21,
∴AD=2×3×0.21=1.26(cm),∴BD=AB-AD=3.5-1.26=2.24(cm)
14、解:在直角三角形中,由勾股定理可得:直角三角形的斜边长为3
m,所以矩形塑料薄膜的面积是:3×12=36(m2)
15、解:根据题意得:Rt△ADE≌Rt△AEF,∴∠AFE=90°,AF=10
cm,EF=DE,设CE=x
cm,则DE=EF=CD-CE=8-x,在Rt△ABF中由勾股定理得:AB2+BF2=AF2,即82+BF2=102,∴BF=6
cm,∴CF=BC-BF=10-6=4(cm),在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,即(8-x)2=x2+42,∴64-16x+x2=x2+16,∴x=3(cm),即CE=3
cm
180
150
60
60
A
B
C
图1
a
b
c
l
图2
图3
图4
图5(2)
图5(1)
图6
A
B
C
图7
图8
图9
图10
P
A
M
N
图11
图12
A
B
C
D
图13
B
图1
B
图14
B
图1
B
图15
图16(2)
图16(1)
北
东
图17
D
家
邮局
书店
图18
图19
图20
图21
图22
A
C
专题一:勾股定理
考点分析:
勾股定理单独命题的题目较少,常与方程、函数,四边形等知识综合在一起考查,在中考试卷中的常见题型为填空题、选择题和较简单的解答题
典例剖析
例1.(1)如图1是一个外轮廓为矩形的机器零件
平面示意图,根据图中的尺寸(单位:),计算
两圆孔中心和的距离为______.
(2)如图2,直线上有三个正方形,若
的面积分别为5和11,则的面积为( )
A.4
B.6
C.16
D.55
分析:本题结合图中的尺寸直接运用勾股定理计算即可.
解:(1)由已知得:AC=150-60=90,BC=180-60=120,由勾股定理得:
AB2=902+1202=22500,所以AB=150(mm)
(2)由勾股定理得:b=a+c=5+11=16,故选C.
点评:以上两例都是勾股定理的直接运用,当已知直角三角形的两边,求第三边时,往往要借助于勾股定理来解决.
例2.如图3,正方形网格的每一个小正方形的边长都是1,试求的度数.
解:连.,,
(SAS).
.
由勾股定理,得:,,
,(SSS).
.
由图可知为等腰直角三角形..
即.
点评:由于在正方形网格中,它有两个主要特征:(1)任何格点之间的线段都是某正方形或长方形的边或对角线,所以格点间的任何线段长度都能求得.
(2)利用正方形的性质,我们很容易知道一些特殊的角,如450、900、1350,便一目了然.以上两例就是根据网格的直观性,再结合图形特点,运用勾股定理进行计算,易求得线段和角的特殊值,重点考查学生的直觉观察能力和数形结合的能力.
专练一:
1、△ABC中,∠A:∠B:∠C=2:1:1,a,b,c分别是∠A、∠B、∠C的对边,则下列各等式中成立的是(
)
(A);(B);
(C);
(D)
2、若直角三角形的三边长分别为2,4,x,则x的可能值有(
)
(A)1个;
(B)2个;
(C)3个;
(D)4个
3、一根旗杆在离底面4.5米的地方折断,旗杆顶端落在离旗杆底部6米处,则旗杆折断前高为(
)
(A)10.5米;
(B)7.5米;
(C)12米;
(D)8米
4、下列说法中正确的有(
)
(1)如果∠A+∠B+∠C=3:4:5,则△ABC是直角三角形;(2)如果∠A+∠B=∠C,那么△ABC是直角三角形;(3)如果三角形三边之比为6:8:10,则ABC是直角三角形;(4)如果三边长分别是,则ABC是直角三角形。
(A)1个;
(B)2个;
(C)3个;
(D)4个
5、如图4是某几何体的三视图及相关数据,则判断正确的是(
)
A.
a>c
B.b>c
C.4a2+b2=c2
D.a2+b2=c2
6、已知直角三角形两边长分别为3、4,则第三边长为
.
7、已知直角三角形的两直角边之比为3:4,斜边为10,则直角三角形的两直角边的长分别为
.
8、利用图5(1)或图5(2)两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为
,该定理的结论其数学表达式是
.
9、一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为
米(答案可保留根号).
10、如图6,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积为1,按上述方法所作的正方形的面积依次为,…,(n为正整数),那么第8个正方形的面积
=_______。
11、如图7,在ΔABC中,AB=AC=10,BC=8.用尺规作图
作BC边上的中线AD(保留作图痕迹,不要求写作法、证明),
并求AD的长.
12、已知一个等腰三角形的底边和腰的长分别为12
cm和10
cm,求这个三角形的面积.
13、在△ABC中,∠C=90°,AC=2.1
cm,BC=2.8
cm
(1)求这个三角形的斜边AB的长和斜边上的高CD的长.
(2)求斜边被分成的两部分AD和BD的长.
14、如图8:要修建一个育苗棚,棚高h=1.8
m,棚宽a=2.4
m,棚的长为12
m,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
15、如图9,已知长方形ABCD中AB=8
cm,BC=10
cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
专题二:一定是直角三角形吗
考点分析:
本部分内容是勾股定理及其逆定理的应用,它在中考试卷中不单独命题,常与其它知识综合命题
典例剖析
例1.如图10,A、B两点都与平面镜相距4米,且A、B两点相距6米,一束光线由A射向平面镜反射之后恰巧经过B点,求B点到入射点的距离.
分析:此题要用到勾股定理,全等三角形,轴对称及物理上的光的反射的知识.
解:作出B点关于CD的对称点B′,连结AB′,交CD于点O,则O点就是光的入射点,因为B′D=DB,所以B′D=AC,∠B′DO=∠OCA=90°,∠B′=∠CAO
所以△B′DO≌△ACO(SSS),则OC=OD=AB=×6=3米,连结OB,在Rt△ODB中,OD2+BD2=OB2,所以OB2=32+42=52,即OB=5(米),所以点B到入射点的距离为5米.
评注:这是以光的反射为背景的一道综合题,涉及到许多几何知识,由此可见,数学是学习物理的基础
例2.如果只给你一把带刻度的直尺,你是否能检验∠MPN是不是直角,简述你的作法.
分析:只有一把刻度尺,只能用这把刻度尺量取线段的长度,若∠P是一个直角,∠P所在的三角形必是个直角三角形,这就提示我们把∠P放在一个三角形中,利用勾股定理的逆定理来解决此题.
作法:①在射线PM上量取PA=3㎝,确定A点,
在射线PN上量取PB=4㎝,确定B点.
②连结AB得△PAB.
③用刻度尺量取AB的长度,
如果AB恰为5㎝,则说明∠P是直角,否则∠P不是直角.
理由:PA=3㎝,PB=4㎝,PA+PB=3+4=5,
若AB=5㎝,则PA+PB=AB,根据勾股定理的逆定理得△PAB是直角三角形,∠P是直角.
说明:这是一道动手操作题,是勾股定理的逆定理在现实生活中的一个典型应用.学生既要会动手操作,又必须能够把操作的步骤完整的表述出来,同时要清楚每个操作题的理论基础.
专练二:
1.做一做:作一个三角形,使三边长分别为3
cm,4
cm,5
cm,哪条边所对的角是直角?为什么?
2.断一断:设三角形的三边分别等于下列各组数:
①7,8,10
②7,24,25
③12,35,37
④13,11,10
(1)请判断哪组数所代表的三角形是直角三角形,为什么?
(2)把你判断是Rt△的哪组数作出它所表示的三角形,并用量角器来进行验证.
3.算一算:.一个零件的形状如图12,已知AC=3㎝,AB=4㎝,BD=12㎝,
求:CD的长.
4.一个零件的形状如图13所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
5.如图14,等边三角形ABC内一点P,AP=3,BP=4,CP=5,求∠APB的度数.
6.若△ABC的三边长为a,b,c,根据下列条件判断△ABC的形状.
(1)a2+b2+c2+200=12a+16b+20c
(2)a3-a2b+ab2-ac2+bc2-b3=0
7.请在由边长为1的小正三角形组成的虚线网格中,画出1
个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形.
8.为筹备迎新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图15,已知圆筒高108㎝,其截面周长为36㎝,如果在表面缠绕油纸4圈,应裁剪多长油纸.
专题三:勾股定理的应用
考点分析:
勾股定理在实际生活中的应用较为广泛,它常常单独命题,有时也与方程、函数,四边形等知识综合在一起考查,在中考试卷中的常见题型为填空题、选择题和较简单的解答题
典例剖析
例1.如图16(1)所示,一个梯子AB长2.5米,
顶端A靠在墙AC上,这时梯子下端B与墙角C距离
为1.5米,梯子滑动后停在DE位置上,如图10(2)所示,
测得得BD=0.5米,求梯子顶端A下落了多少米?
分析:梯子顶端A下落的距离为AE,
即求AE的长.已知AB和BC,根据勾股定理可求AC,
只要求出EC即可。
解:在Rt△ACB中,AC2=AB2-BC2=2.52-1.52=4,
∴AC=2,∵BD=0.5,∴CD=2
∴EC=1.5,
,所以,梯子顶端下滑了0.5米.
点评:在实际生活、生产及建筑中,当人们自身高度达不到时,往往要借助于梯子,这时对梯子的选择,及梯子所能达到的高度等问题,往往要用到勾股定理的知识来解决.但要
注意:考虑梯子的长度不变.
例2.有一根竹竿,
不知道它有多长.
把竹竿横放在一扇门前,
竹竿长比门宽多4尺;把竹竿竖放在这扇门前,
竹竿长比门的高度多2尺;
把竹竿斜放,,竹竿长正好和门的对角线等长.问竹竿长几尺?
分析:只要根据题意,画出图形,然后利用勾股定理,列出方程解之
解:设竹竿长为x尺。则:(x―4)2+(x―2)2=x2
x1=10
,x2=2(不合题意舍去)
答:竹竿长为10尺。
评注:本题是勾股定理与方程的综合应用问题,它综合考查了同学们的建模思想和方法的理解和运用,符合新课程标准的理念,请注意这类问题!
例3.如图17,客轮在海上以30km/h的速度由向航行,在处测得灯塔的方位角为北偏东,测得处的方位角为南偏东,航行1小时后到达处,在处测得的方位角为北偏东,则到的距离是(
)
A.km;B.km;C.km;D.km
分析:本题是一道以航海为背景的应用题,由已知条件分析易知△ABC
不是直角三角形,这就需要作三角形的高,将非直角三角形转化为直角三角形,
问题便可得到解决.
解:由条件易得:∠C=450,∠ABC=750,则∠A=600,过B作BD⊥AC,
垂足为D,∴△BCD是等腰直角三角形,又∵BC=30km,由勾股定理得:
2CD2=302,∴CD=,∴BD=,设AD=x,则AB=2x,由勾股定理得:BD=,∴=,∴x=,∴AC=+,故选D.
点评:
在航海中,有时需要求两船或船与某地方的距离,以保证航海的安全,有时就需要用勾股定理及判定条件来加以解决,熟练应用勾股定理是解题的关键.
专练三:
1.小明从家走到邮局用了8分钟,然后右转弯用同样的速度走了6分钟到达书店(如图18),已知书店距离邮局640米,那么小明家距离书店
米.
2.一根新生的芦苇高出水面1尺,一阵风吹过,芦苇被吹倒一边,顶端齐至水面,芦苇移动的水平距离为5尺,则水池的深度和芦苇的长度各是
.
3.小明叔叔家承包了一个矩形养鱼池,已知其面积为48m,其对角线长为10m,为建起栅栏,要计算这个矩形养鱼池的周长,你能帮助小明算一算,周长应该是
.
4.求图19所示(单位mm)矩形零件上两孔
中心A和B的距离(精确到0.lmm).
5.假期,小王与同学们在公园里探宝玩游戏,按照游戏中提示的方向,他们从A出发先向正东走了800米,再向正北走了200米,折向正西走300米,再向正北走600米,再向正东走100米,到达了宝藏处B,问A、B间的直线距离是
米.
6.如图20所示,为修铁路需凿通隧道AC,测得∠A=53°,
∠B=37°.AB=5km,BC=4km,若每天凿0.3km,
试计算需要几天才能把隧道AC凿通.
7.如图21,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
8.观察下列表格:
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
……
……
13、b、c
132=b+c
请你结合该表格及相关知识,求出b、c的值。
9.如图22所示的一块地,AD=12m,CD=9m,∠ADC=90°,AB=39m,BC=36m,求这块地的面积.
参考答案
专练一:
1.;2.12,13;
3.28;
5、1000
6.
解:因为∠A=53°,∠B=37°∴∠ACB=90°,
在Rt△ABC中,AC=AB-BC=5-4=9,所以AC=3,需要的时间
(天)
答:需要10天才能把隧道AC凿通。
7.由勾股定理得:AB=10,设CD=x,则DE=x,BD=8-x,BE=4,由勾股定理得:
42+x2=(8-x)2,解得x=3,即CD=3
8.12,5
9.连结AC,在Rt△ADC中,
,
,在△ABC中,AB2=1521
,
答:这块地的面积是216平方米。
专练二:
1.做一做:5
cm所对的角是直角,因为在直角三角形中直角所对边最长.
2.断一断:(1)②③
∵72+242=252,
122+352=372
(2)略
3.解:在直角三角形ABC中,根据勾股定理:BC=AC+AB=3+4=25,在直角三角形CBD中,根据勾股定理:CD=BC+BD=25+12=169,∴CD=13.
4.∵42+32=52,52+122=132,即AB2+BC2=AC2,故∠B=90°,同理,∠ACD=90°
∴S四边形ABCD=S△ABC+S△ACD=×3×4+×5×12=6+30=36.
5.解:如图,以AP为边作等边△APD,连结BD.则∠1=60°-∠BAP=
∠2,
在△ADB和△APC中,
AD=AP.∠1=∠2,AB=AC
∴△ADB≌△ADC(SAS)
∴BD=PC=5,又PD=AP=3,BP=4
∴BP2+PD2=42+32=25=BD2
∴∠BPD=90°
∴∠APB=∠APD+∠BPD=150°
6.(1)∵a2+b2+c2+100=12a+16b+20c,∴(a2-12a+36)+(b2-16b+64)+(c2-20c+100)=0,
即(a-6)2+(b-8)2+(c-10)2=0
∴a-6=0,b-8=0,c-10=0,即a=6,b=8,c=10,而62+82=100=102,∴a2+b2=c2,
∴△ABC为直角三角形.
(2)(a3-a2b)+(ab2-b3)-(ac2-bc2)=0,a2(a-b)+b2(a-b)-c2(a-b)=0,∴(a-b)(a2+b2-c2)=0
∴a-b=0或a2+b2-c2=0,∴此三角形ABC为等腰三角形或直角三角形.
7.解:本题答案不惟一,只要符合要求都可以,以下答案供参考.
8.解:将圆筒展开后成为一个矩形,如图,
整个油纸也随之分成相等4段只需求出AC长
即可,在Rt△ABC中,AB=36,BC=
∴由勾股定理得AC=AB+BC=36+27
∴AC=45,故整个油纸的长为45×4=180(㎝).
专练三:
1、C;2、B;3、B;4、C;5、D;6、5,;7、6,8;8、勾股定理,;9、;10、128;
11、(1)作图略;
(2)在△ABC中,AB=AC,AD是△ABC的中线,∴AD⊥BC,.在Rt△ABD中,AB=10,BD=4,,
.
12、如图:等边△ABC中BC=12
cm,AB=AC=10
cm
作AD⊥BC,垂足为D,则D为BC中点,BD=CD=6
cm,在Rt△ABD中,AD2=AB2-BD2=102-62=64
∴AD=8
cm
∴S△ABD=BC·AD=×12×8=48(cm2)
13、解:(1)∵△ABC中,∠C=90°,AC=2.1
cm,BC=2.8
cm
∴AB2=AC2+BC2=2.12+2.82=12.25
∴AB=3.5
cm,∵S△ABC=AC·BC=AB·CD,∴AC·BC=AB·CD,
∴CD===1.68(cm)
(2)在Rt△ACD中,由勾股定理得:AD2+CD2=AC2,
∴AD2=AC2-CD2=2.12-1.682=(2.1+1.68)(2.1-1.68)
=3.78×0.42=2×1.89×2×0.21=22×9×0.21×0.21,
∴AD=2×3×0.21=1.26(cm),∴BD=AB-AD=3.5-1.26=2.24(cm)
14、解:在直角三角形中,由勾股定理可得:直角三角形的斜边长为3
m,所以矩形塑料薄膜的面积是:3×12=36(m2)
15、解:根据题意得:Rt△ADE≌Rt△AEF,∴∠AFE=90°,AF=10
cm,EF=DE,设CE=x
cm,则DE=EF=CD-CE=8-x,在Rt△ABF中由勾股定理得:AB2+BF2=AF2,即82+BF2=102,∴BF=6
cm,∴CF=BC-BF=10-6=4(cm),在Rt△ECF中由勾股定理可得:EF2=CE2+CF2,即(8-x)2=x2+42,∴64-16x+x2=x2+16,∴x=3(cm),即CE=3
cm
180
150
60
60
A
B
C
图1
a
b
c
l
图2
图3
图4
图5(2)
图5(1)
图6
A
B
C
图7
图8
图9
图10
P
A
M
N
图11
图12
A
B
C
D
图13
B
图1
B
图14
B
图1
B
图15
图16(2)
图16(1)
北
东
图17
D
家
邮局
书店
图18
图19
图20
图21
图22
A
C
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
