人教数学八年级上册 11.1.1三角形的边课件(共22张PPT)
文档属性
| 名称 | 人教数学八年级上册 11.1.1三角形的边课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-15 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
11.1
与三角形有关的线段(第1课时)
11.1.1
三角形的边
检查预习:
三角形的定义是什么?
概念
由不在同一直线上的三条线段首位顺次相接所组成的图形叫做三角形.
注意:
(1)三条线段
(2)不在同一直线上
(3)首位顺次相接
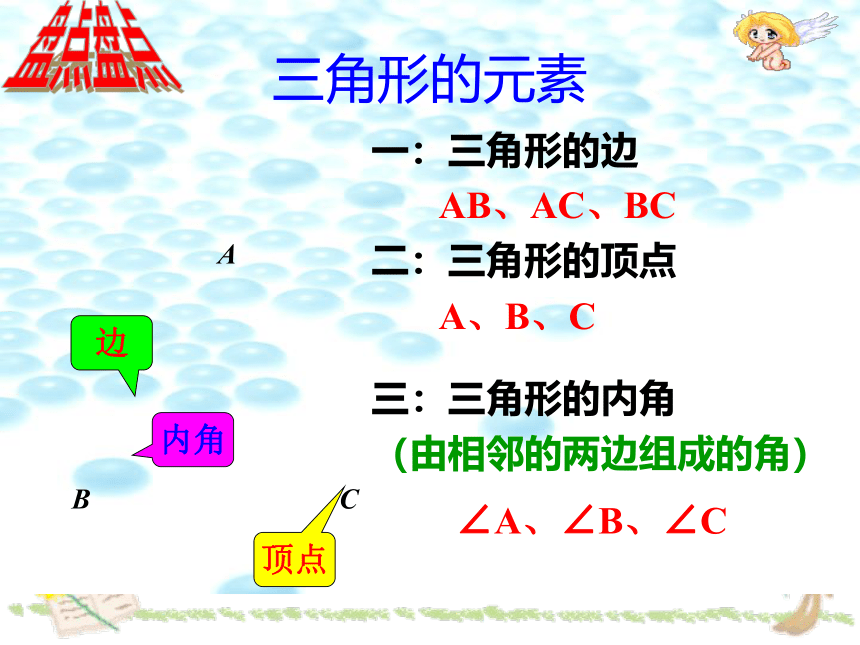
三角形的元素
一:三角形的边
A
B
C
盘点
AB、AC、BC
二:三角形的顶点
A、B、C
边
顶点
三:三角形的内角
(由相邻的两边组成的角)
∠A、∠B、∠C
内角
三角形的记作
如图,顶点是A、B、C的三角形,记作“△ABC”,读作“三角形ABC”.
几何语言
A
B
C
情况一:按角分
思考:三角形可以如何进行分类?
三个角都是锐角的三角形是锐角三角形;
一个角是直角的三角形是直角三角形;
一个角是钝角的三角形是钝角三角形.
思考:三角形可以如何进行分类?
情况二:按边分
三边都相等的三角形叫做等边三角形;
有两条边相等的三角形叫做等腰三角形;
三边都不相等的三角形叫做不等边三角形.
在等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰与底边的的夹角叫做底角.
等腰三角形的元素
A
B
C
等边三角形
A
B
C
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
三角形的分类
1.
按角分
小结
锐角三角形
直角三角形
钝角三角形
2.
按边分
不等边三角形
等腰三角形
底与腰不等的等腰三角形
等边三角形
斜三角形
任意画一个△ABC,假设一条小虫从点B出发,沿三角形的边爬到点C,它有几条线路可以选择?各条线路的长一样吗?
探究
A
B
C
AB+AC
BC
>
想一想,为什么?
两点的所有连线中,线段最短.
同理:AC+BC>AB,AB+BC>AC.
探
究
A
B
C
AB+AC>BC,
①
AC+BC>AB,
②
AB+BC>AC.
③
AC-AB<BC,
④
BC-AC<AB,
⑤
BC-AB<AC.
⑥
问:式子④⑤⑥成立吗?
成立
三角形的三边关系:
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边.
例
用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
(1)解:设底边长为x
cm,腰长2x
cm.
x+2x+2x=18
解得
x=3.6
∴三边长分别为3.6cm、7.2cm、7.2cm.
例
用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
(2)解:①如果4cm长的边为底边,那么设腰长为x
cm.
4+2x=18
解得
x=7
则底边的取值范围为7-7<x<7+7
∴三边长分别为4cm、7cm、7cm
②如果4cm长的边为腰,那么设底边长为y
cm.
2×4+y=18
解得
y=10
又∵底边的取值范围为4-4<y<4+4
∴不能围成腰长为4cm的等腰三角形
谈谈你的收获!
1.三角形的定义:
小
结
由不在同一直线上的三条线段首位顺次相接所组成的图形叫做三角形.
2.三角形的分类:
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
等腰三角形
底与腰不等的等腰三角形
等边三角形
3.三角形的三边关系:
三角形任意两边之和大于第三边,任意两边之差小于第三边.
1.如图所示,共有
个三角形.
以AD为一边的三角形有
;
∠C是△ADC的
边的对角;AE是△ABE中∠
的对边.
课后思考
B
C
A
D
E
6
△ABD、△ADE、△ACD
AD
B
2.判断下列每组线段能否组成三角形(能的在括号中打“√”,不能的打“×”.
(1)a=5,b=4,c=3;
(
)
(2)a=7,b=2,c=4;
(
)
(3)a=6,b=6,c=12;
(
)
(4)a=6,b=5,c=5.
(
)
课后思考
√
×
×
√
3.已知a、b、c为△ABC的三边长,满足(b-2)?+
c-3
=0,且
a
为方程
x-4
=2的解,求△ABC的周长,并判断△ABC的形状.
课后思考
天生我才
(想一想
x
可以取哪些值?)
下课了!
再
见
11.1
与三角形有关的线段(第1课时)
11.1.1
三角形的边
检查预习:
三角形的定义是什么?
概念
由不在同一直线上的三条线段首位顺次相接所组成的图形叫做三角形.
注意:
(1)三条线段
(2)不在同一直线上
(3)首位顺次相接
三角形的元素
一:三角形的边
A
B
C
盘点
AB、AC、BC
二:三角形的顶点
A、B、C
边
顶点
三:三角形的内角
(由相邻的两边组成的角)
∠A、∠B、∠C
内角
三角形的记作
如图,顶点是A、B、C的三角形,记作“△ABC”,读作“三角形ABC”.
几何语言
A
B
C
情况一:按角分
思考:三角形可以如何进行分类?
三个角都是锐角的三角形是锐角三角形;
一个角是直角的三角形是直角三角形;
一个角是钝角的三角形是钝角三角形.
思考:三角形可以如何进行分类?
情况二:按边分
三边都相等的三角形叫做等边三角形;
有两条边相等的三角形叫做等腰三角形;
三边都不相等的三角形叫做不等边三角形.
在等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰与底边的的夹角叫做底角.
等腰三角形的元素
A
B
C
等边三角形
A
B
C
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
三角形的分类
1.
按角分
小结
锐角三角形
直角三角形
钝角三角形
2.
按边分
不等边三角形
等腰三角形
底与腰不等的等腰三角形
等边三角形
斜三角形
任意画一个△ABC,假设一条小虫从点B出发,沿三角形的边爬到点C,它有几条线路可以选择?各条线路的长一样吗?
探究
A
B
C
AB+AC
BC
>
想一想,为什么?
两点的所有连线中,线段最短.
同理:AC+BC>AB,AB+BC>AC.
探
究
A
B
C
AB+AC>BC,
①
AC+BC>AB,
②
AB+BC>AC.
③
AC-AB<BC,
④
BC-AC<AB,
⑤
BC-AB<AC.
⑥
问:式子④⑤⑥成立吗?
成立
三角形的三边关系:
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边.
例
用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
(1)解:设底边长为x
cm,腰长2x
cm.
x+2x+2x=18
解得
x=3.6
∴三边长分别为3.6cm、7.2cm、7.2cm.
例
用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
(2)解:①如果4cm长的边为底边,那么设腰长为x
cm.
4+2x=18
解得
x=7
则底边的取值范围为7-7<x<7+7
∴三边长分别为4cm、7cm、7cm
②如果4cm长的边为腰,那么设底边长为y
cm.
2×4+y=18
解得
y=10
又∵底边的取值范围为4-4<y<4+4
∴不能围成腰长为4cm的等腰三角形
谈谈你的收获!
1.三角形的定义:
小
结
由不在同一直线上的三条线段首位顺次相接所组成的图形叫做三角形.
2.三角形的分类:
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
等腰三角形
底与腰不等的等腰三角形
等边三角形
3.三角形的三边关系:
三角形任意两边之和大于第三边,任意两边之差小于第三边.
1.如图所示,共有
个三角形.
以AD为一边的三角形有
;
∠C是△ADC的
边的对角;AE是△ABE中∠
的对边.
课后思考
B
C
A
D
E
6
△ABD、△ADE、△ACD
AD
B
2.判断下列每组线段能否组成三角形(能的在括号中打“√”,不能的打“×”.
(1)a=5,b=4,c=3;
(
)
(2)a=7,b=2,c=4;
(
)
(3)a=6,b=6,c=12;
(
)
(4)a=6,b=5,c=5.
(
)
课后思考
√
×
×
√
3.已知a、b、c为△ABC的三边长,满足(b-2)?+
c-3
=0,且
a
为方程
x-4
=2的解,求△ABC的周长,并判断△ABC的形状.
课后思考
天生我才
(想一想
x
可以取哪些值?)
下课了!
再
见
