人教版七年级数学上册1.4.1有理数的乘法-课件(共18张PPT)
文档属性
| 名称 | 人教版七年级数学上册1.4.1有理数的乘法-课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 973.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-15 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
1.4.1有理数的乘法
(1)(-5)×(-3)
(2)(-7)×4
(3)(-3)×0
引入新知
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
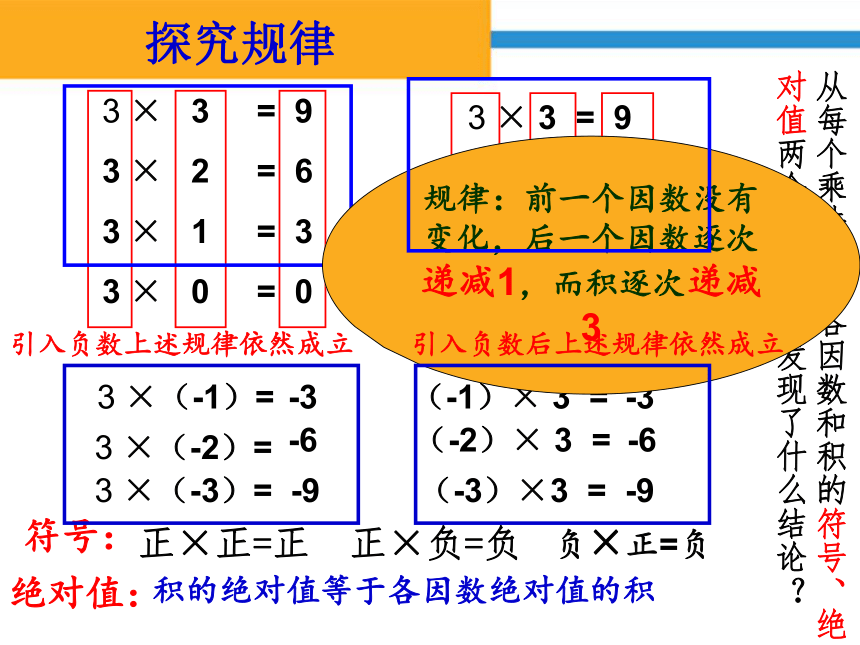
3
×
3
=
9
3
×
2
=
6
3
×
1
=
3
3
×
0
=
0
3
×(-1)=
3
×(-2)=
3
×(-3)=
-3
-6
-9
符号:
积的绝对值等于各因数绝对值的积
绝对值:
探究规律
3
×
3
=
9
2
×
3
=
6
1
×
3
=
3
0
×
3
=
0
(-1)×
3
=
(-2)×
3
=
(-3)×3
=
-3
-6
-9
正×正=正
正×负=负
从每个乘法算式各因数和积的符号、绝对值两个角度,你发现了什么结论?
规律:前一个因数没有变化,后一个因数逐次递减1,而积逐次递减3
引入负数上述规律依然成立
负×正=负
引入负数后上述规律依然成立
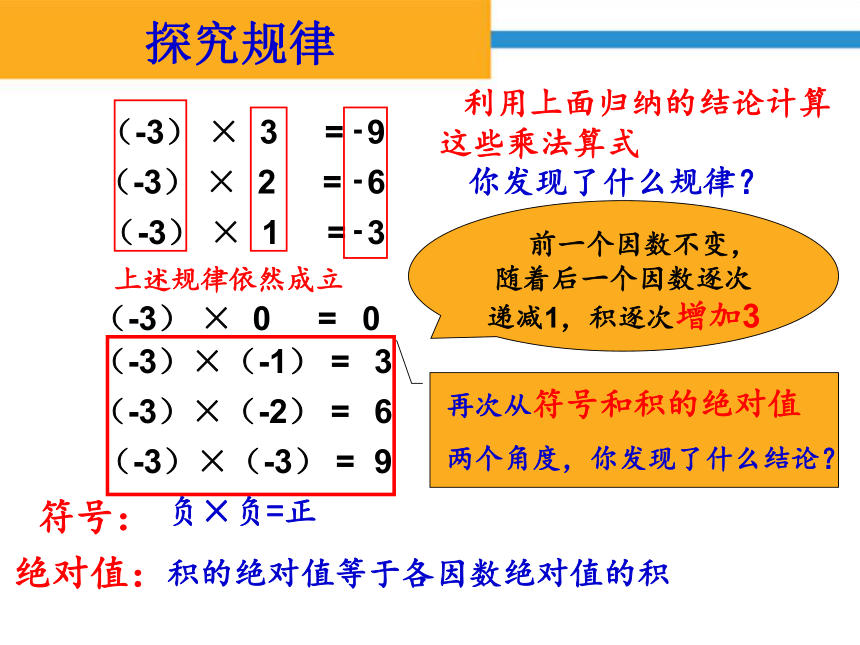
(-3)
×
2
=
(-3)
×
3
=
探究规律
(-3)
×
1
=
(-3)
×
0
=
9
6
3
0
(-3)×(-1)
=
(-3)×(-2)
=
(-3)×(-3)
=
3
6
9
利用上面归纳的结论计算这些乘法算式
你发现了什么规律?
前一个因数不变,随着后一个因数逐次递减1,积逐次增加3
再次从符号和积的绝对值
两个角度,你发现了什么结论?
符号:
绝对值:
负×负=正
积的绝对值等于各因数绝对值的积
-
-
-
上述规律依然成立
3
×3
=
9
3
×2
=
6
3
×1
=
3
3
×(-1)=
3
×(-2)=
3
×(-3)=
(-3)
×
0
=
-3
-6
-9
-9
-6
-3
0
(-1)
×
3
=
(-3)
×
3
=
(-2)
×
3
=
(-3)
×(-1)=
(-3)
×(-3)=
(-3)
×(-2)=
3
6
9
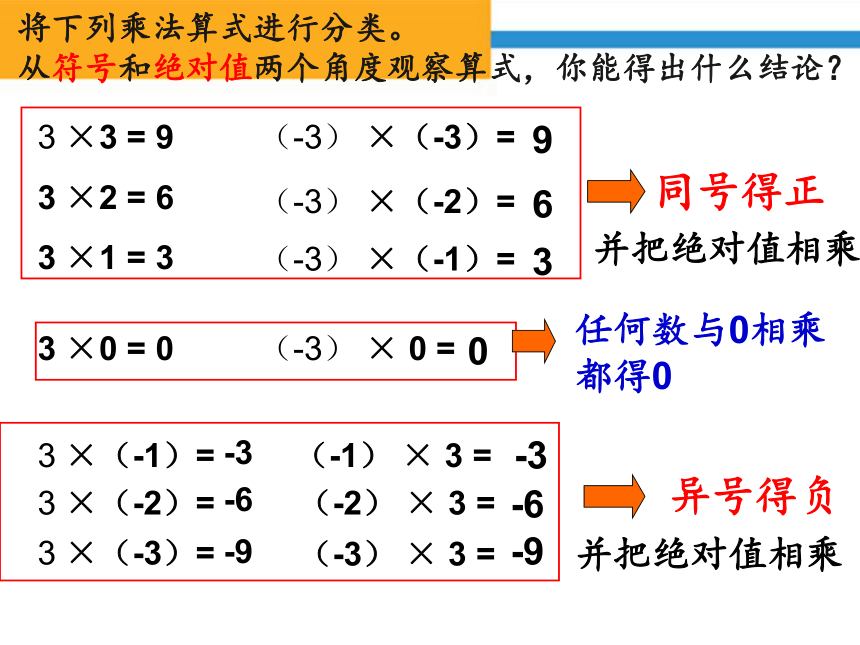
同号得正
3
×0
=
0
异号得负
任何数与0相乘都得0
并把绝对值相乘
并把绝对值相乘
将下列乘法算式进行分类。
从符号和绝对值两个角度观察算式,你能得出什么结论?
有理数乘法法则:
1、两数相乘,同号得正,异号得负,
并把绝对值相乘。
2、任何数与0相乘都得0
(1)
(-5)x(-3)………….同号两数相乘
(-5)x(-3)=+(
)…………得正
5
x
3=
15………………把绝对值相乘
所以
(-5)
x
(-3)=
15
(2)
(-7)x
4……____________________
(-7)x
4
=
-(
)………___________
7
x
4
=
28………_____________
所以
(-7)x
4
=
____________
异号两数相乘
得负
把绝对值相乘
-28
应用法则,验证猜想
例1、计算
(1)
9×8
;
(2)
(?9)×8
;
解:(1)
9×
8
(2)
(?9)×8
(3)
9
×(-8)(4)(-9)×
(-8)
=
72
求解步骤;
1、确定积的符号
2、把绝对值相乘
(3)
9×(-8)
(4)(-9)×(-8)
=
?
72
=
?
=
+
=
+
=
?
(9×8)
(9×8)
(9×8)
(9×8)
=
72
=
?
72
应用法则
用“>”
“<”或“=”号填空:
1﹑如果
a>0,
b>0,
那么ab(
)0;
2﹑如果
a>0,
b<0,
那么ab(
)0;
3﹑如果
a<0,
b>0,
那么ab(
)0;
4﹑如果
a<0,
b<0,
那么ab(
)0;
5﹑如果
a
=
0,
b≠0,
那么ab(
)0.
应用法则
>
<
<
>
=
例2、计算
(1)2018
x1
(2)
-
2018
x1
(3)
2018
x(-1)
(4)
-
2018
x(-1)
(5)
(1)、1乘以一个数仍得这个数,-1乘以一个数得这个
数的相反数。
(3)、两个带分数相乘,一般要化成假分数以便约分。
(2)、含负号的两因数相乘时,第一个因数前面可以不加括号,但后面的因数必须添加括号。如(4)若写成
-2018
x-1是错误的,因为两个运算符号是不能连在一起写的。
=2018
=-2018
=-2018
=2018
谈谈你的发现
=+(
)
=
3
例3
计算:
(1)
×2 ; (2)
(-
)
×
(
-2
)
。
解:(1)
×2 = 1
(2)(-
)×(-2)=1
观察两题有何特点?
有理数中仍然有:乘积是1的两个数互为倒数.
数a(a≠0)的倒数是什么?
(a≠0时,a的倒数是
)
温馨提醒:互为倒数的两个数是同号的,正数的倒数是正数,负数的倒数是负数,零没有倒数。
当堂测试
D
C
C
D
1.计算?1×2的结果是( )
A.1
B.2
C.?3
D.?2
2.计算(?3)×|?2|的结果等于( )
A.6
B.5
C.?6
D.?5
3.以下各数中,填入□中能使(?
)×□=?2成立的是( )
A.?1
B.2
C.4
D.?4
4.下列四个有理数
、0、1、?2,任取两个相乘,积最小为( )
A.
B.0
C.?1
D.?2
二.填空题
5.已知|a|=2,|b|=5,且ab<0,那么a+b的值为
.
6.若a<b<0,则(a+b)(a?b)
0.
7.|?1.5|的倒数是
8.若a、b是互为倒数,则2ab?5=
3或-3
>
-3
三、计算:
(1)(?1.2)×(?3)
(2)(
)×(
)
(3)15×(?
)
(4)(
)×0
(5)(?2.5)×
=3.6
=6
=-6
=0
四.规定a﹡b=5a+2b-1,求(-
4)﹡6的值
解:(-
4)﹡6=5×(-
4)+2×6-1
=-9
=-20+12-1
5.观察下列等式
,
,
,
将以上三个等式两边分别相得:
.
(1)猜想并写出
.
(2)直接写出下列各式的计算结果:
①
②
乘积是1的两个数互为倒数
1、两数相乘,同号得正,异号得负,并把绝对值相乘。
2、任何数与0相乘,都得0
有理数的乘法
法则
倒数
解题步骤
1、符号
2、绝对值
归纳总结
谢谢!
1.4.1有理数的乘法
(1)(-5)×(-3)
(2)(-7)×4
(3)(-3)×0
引入新知
我们已经熟悉正数及0的乘法运算,引入负数以后,怎样进行有理数的乘法运算呢?
3
×
3
=
9
3
×
2
=
6
3
×
1
=
3
3
×
0
=
0
3
×(-1)=
3
×(-2)=
3
×(-3)=
-3
-6
-9
符号:
积的绝对值等于各因数绝对值的积
绝对值:
探究规律
3
×
3
=
9
2
×
3
=
6
1
×
3
=
3
0
×
3
=
0
(-1)×
3
=
(-2)×
3
=
(-3)×3
=
-3
-6
-9
正×正=正
正×负=负
从每个乘法算式各因数和积的符号、绝对值两个角度,你发现了什么结论?
规律:前一个因数没有变化,后一个因数逐次递减1,而积逐次递减3
引入负数上述规律依然成立
负×正=负
引入负数后上述规律依然成立
(-3)
×
2
=
(-3)
×
3
=
探究规律
(-3)
×
1
=
(-3)
×
0
=
9
6
3
0
(-3)×(-1)
=
(-3)×(-2)
=
(-3)×(-3)
=
3
6
9
利用上面归纳的结论计算这些乘法算式
你发现了什么规律?
前一个因数不变,随着后一个因数逐次递减1,积逐次增加3
再次从符号和积的绝对值
两个角度,你发现了什么结论?
符号:
绝对值:
负×负=正
积的绝对值等于各因数绝对值的积
-
-
-
上述规律依然成立
3
×3
=
9
3
×2
=
6
3
×1
=
3
3
×(-1)=
3
×(-2)=
3
×(-3)=
(-3)
×
0
=
-3
-6
-9
-9
-6
-3
0
(-1)
×
3
=
(-3)
×
3
=
(-2)
×
3
=
(-3)
×(-1)=
(-3)
×(-3)=
(-3)
×(-2)=
3
6
9
同号得正
3
×0
=
0
异号得负
任何数与0相乘都得0
并把绝对值相乘
并把绝对值相乘
将下列乘法算式进行分类。
从符号和绝对值两个角度观察算式,你能得出什么结论?
有理数乘法法则:
1、两数相乘,同号得正,异号得负,
并把绝对值相乘。
2、任何数与0相乘都得0
(1)
(-5)x(-3)………….同号两数相乘
(-5)x(-3)=+(
)…………得正
5
x
3=
15………………把绝对值相乘
所以
(-5)
x
(-3)=
15
(2)
(-7)x
4……____________________
(-7)x
4
=
-(
)………___________
7
x
4
=
28………_____________
所以
(-7)x
4
=
____________
异号两数相乘
得负
把绝对值相乘
-28
应用法则,验证猜想
例1、计算
(1)
9×8
;
(2)
(?9)×8
;
解:(1)
9×
8
(2)
(?9)×8
(3)
9
×(-8)(4)(-9)×
(-8)
=
72
求解步骤;
1、确定积的符号
2、把绝对值相乘
(3)
9×(-8)
(4)(-9)×(-8)
=
?
72
=
?
=
+
=
+
=
?
(9×8)
(9×8)
(9×8)
(9×8)
=
72
=
?
72
应用法则
用“>”
“<”或“=”号填空:
1﹑如果
a>0,
b>0,
那么ab(
)0;
2﹑如果
a>0,
b<0,
那么ab(
)0;
3﹑如果
a<0,
b>0,
那么ab(
)0;
4﹑如果
a<0,
b<0,
那么ab(
)0;
5﹑如果
a
=
0,
b≠0,
那么ab(
)0.
应用法则
>
<
<
>
=
例2、计算
(1)2018
x1
(2)
-
2018
x1
(3)
2018
x(-1)
(4)
-
2018
x(-1)
(5)
(1)、1乘以一个数仍得这个数,-1乘以一个数得这个
数的相反数。
(3)、两个带分数相乘,一般要化成假分数以便约分。
(2)、含负号的两因数相乘时,第一个因数前面可以不加括号,但后面的因数必须添加括号。如(4)若写成
-2018
x-1是错误的,因为两个运算符号是不能连在一起写的。
=2018
=-2018
=-2018
=2018
谈谈你的发现
=+(
)
=
3
例3
计算:
(1)
×2 ; (2)
(-
)
×
(
-2
)
。
解:(1)
×2 = 1
(2)(-
)×(-2)=1
观察两题有何特点?
有理数中仍然有:乘积是1的两个数互为倒数.
数a(a≠0)的倒数是什么?
(a≠0时,a的倒数是
)
温馨提醒:互为倒数的两个数是同号的,正数的倒数是正数,负数的倒数是负数,零没有倒数。
当堂测试
D
C
C
D
1.计算?1×2的结果是( )
A.1
B.2
C.?3
D.?2
2.计算(?3)×|?2|的结果等于( )
A.6
B.5
C.?6
D.?5
3.以下各数中,填入□中能使(?
)×□=?2成立的是( )
A.?1
B.2
C.4
D.?4
4.下列四个有理数
、0、1、?2,任取两个相乘,积最小为( )
A.
B.0
C.?1
D.?2
二.填空题
5.已知|a|=2,|b|=5,且ab<0,那么a+b的值为
.
6.若a<b<0,则(a+b)(a?b)
0.
7.|?1.5|的倒数是
8.若a、b是互为倒数,则2ab?5=
3或-3
>
-3
三、计算:
(1)(?1.2)×(?3)
(2)(
)×(
)
(3)15×(?
)
(4)(
)×0
(5)(?2.5)×
=3.6
=6
=-6
=0
四.规定a﹡b=5a+2b-1,求(-
4)﹡6的值
解:(-
4)﹡6=5×(-
4)+2×6-1
=-9
=-20+12-1
5.观察下列等式
,
,
,
将以上三个等式两边分别相得:
.
(1)猜想并写出
.
(2)直接写出下列各式的计算结果:
①
②
乘积是1的两个数互为倒数
1、两数相乘,同号得正,异号得负,并把绝对值相乘。
2、任何数与0相乘,都得0
有理数的乘法
法则
倒数
解题步骤
1、符号
2、绝对值
归纳总结
谢谢!
