沪教版(上海)九年级数学上册24.3三角形一边的平行线-课件(共16张PPT)
文档属性
| 名称 | 沪教版(上海)九年级数学上册24.3三角形一边的平行线-课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 418.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-15 21:02:29 | ||
图片预览

文档简介
(共16张PPT)
24.3三角形一边的平行线
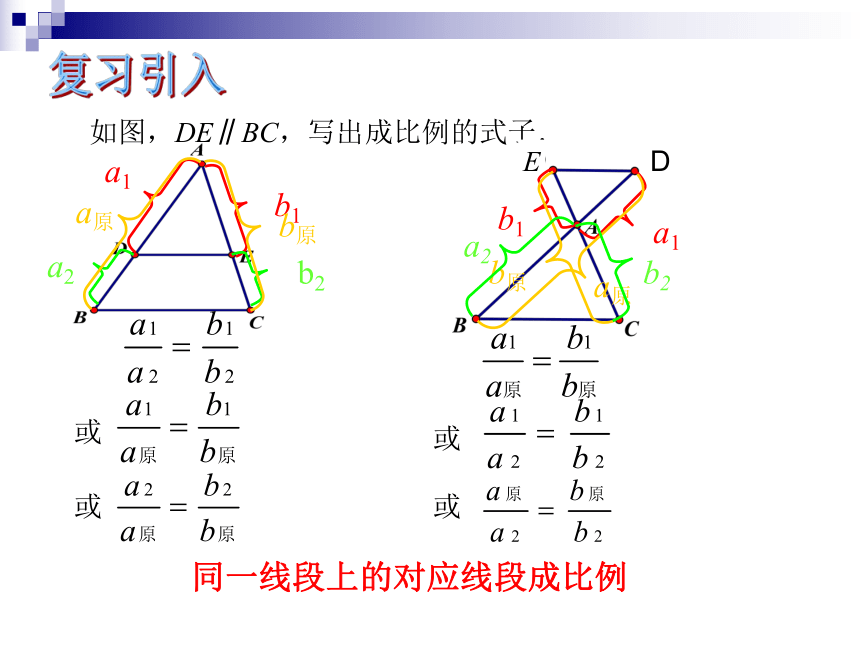
如图,DE∥BC,写出成比例的式子.
复习引入
E
D
a1
a2
b1
b2
a原
b原
a1
a原
b1
b原
a2
b2
同一线段上的对应线段成比例
或
或
或
或
分析:由上节课学习的三角形一边的平行线性质定理
。比例线段分别在三角形两边所在的直线上,因此,考虑将DE平移到BC边上去
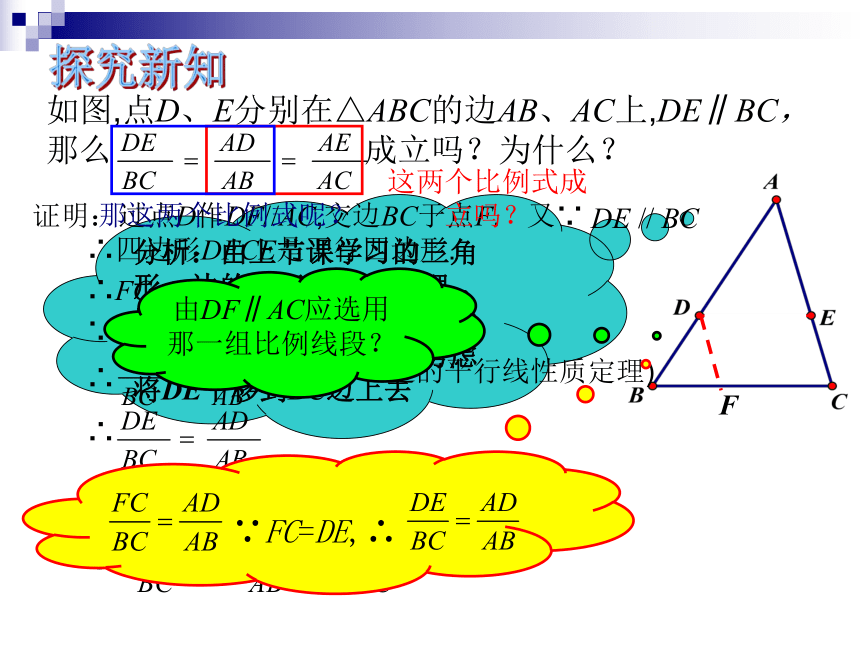
探究新知
如图,点D、E分别在△ABC的边AB、AC上,DE∥BC,
那么
成立吗?为什么?
证明:过点D作DF//AC,交边BC于点F.
又∵
∴四边形DFCE是平行四边形.
∴FC=DE.
∵DF//AC
∴
(三角形一边的平行线性质定理)
∴
由DE∥BC,得
∴
F
这两个比例式成立吗?
那这两个比例式呢?
∵FC=DE,∴
由DF∥AC应选用那一组比例线段?
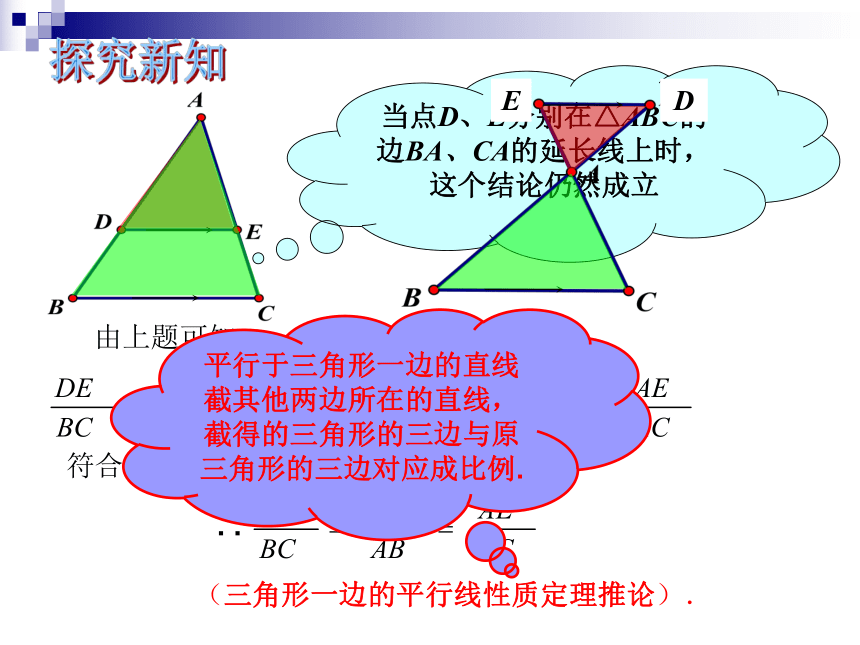
探究新知
由上题可知
当点D、E分别在△ABC的边BA、CA的延长线上时,这个结论仍然成立
符合语言:
∵DE//BC,
∴
(三角形一边的平行线性质定理推论).
D
E
平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.
新知运用
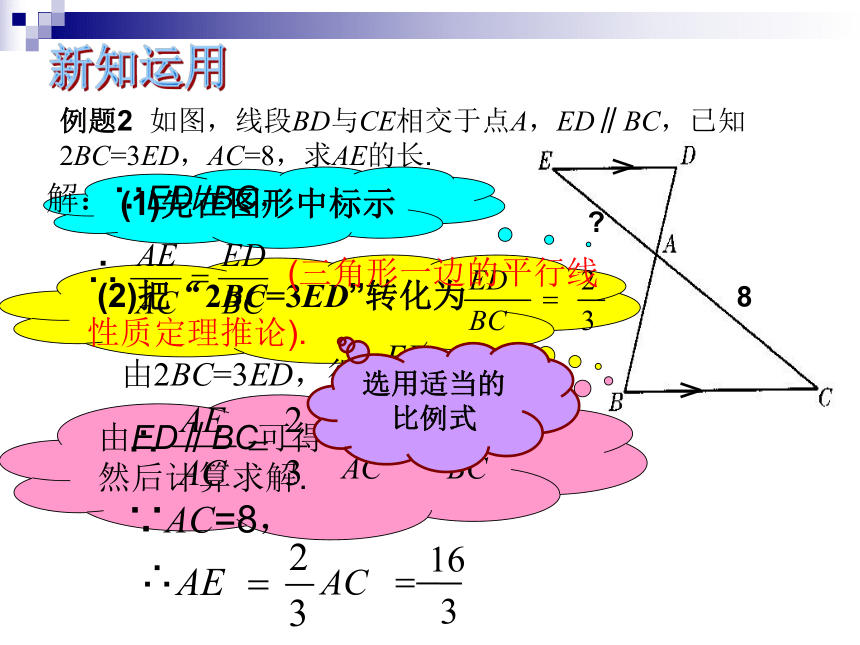
例题2
如图,线段BD与CE相交于点A,ED∥BC,已知2BC=3ED,AC=8,求AE的长.
(1)先在图形中标示
8
?
(2)把“2BC=3ED”转化为
由ED∥BC可得
然后计算求解.
解:∵ED//BC,
∴
(三角形一边的平行线
性质定理推论).
由2BC=3ED,得
∴
∵AC=8,
选用适当的比例式
∴
3
16
=
AC
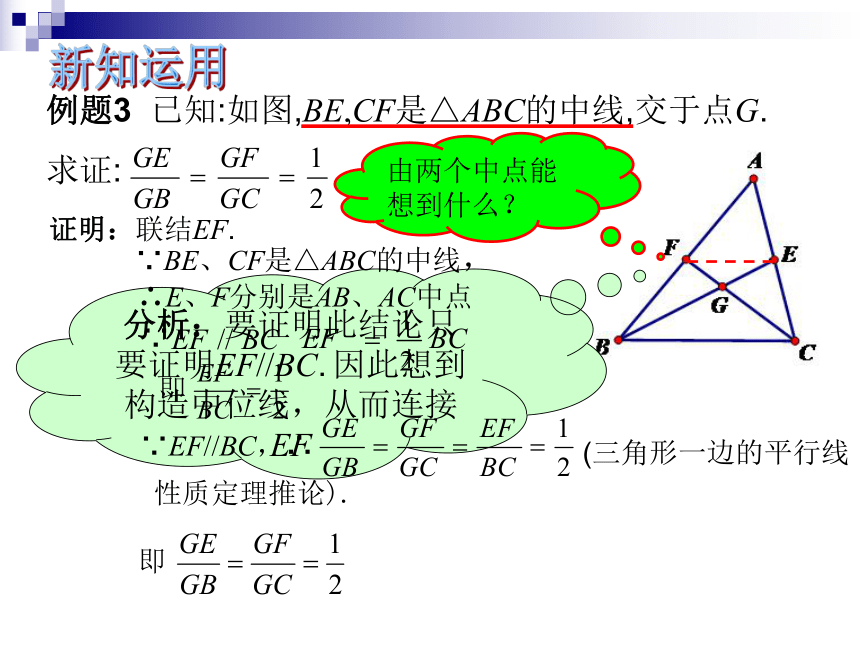
分析:要证明此结论只要证明EF//BC.
因此想到构造中位线,从而连接EF
新知运用
例题3
已知:如图,BE,CF是△ABC的中线,交于点G.
求证:
证明:联结EF.
∵BE、CF是△ABC的中线,
即
∵EF//BC,∴
即
由两个中点能想到什么?
∴E、F分别是AB、AC中点
∵
(三角形一边的平行线
性质定理推论).
新知运用
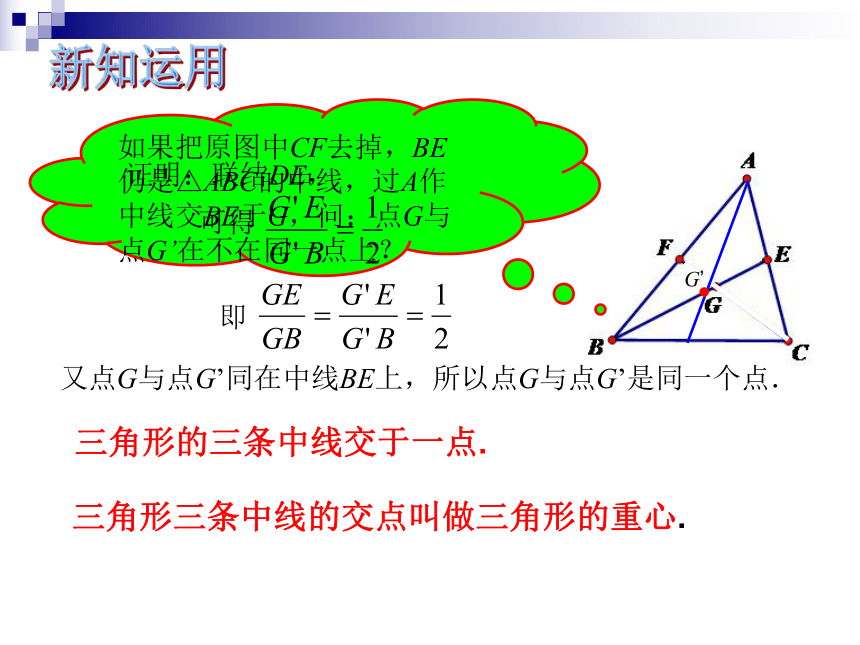
如果把原图中CF去掉,BE仍是△ABC的中线,过A作中线交BE于G,问:点G与点G’在不在同一点上?
证明:联结DE,
可得
又点G与点G’同在中线BE上,所以点G与点G’是同一个点.
即
三角形的三条中线交于一点.
三角形三条中线的交点叫做三角形的重心.
G’
三角形重心定理:
三角形的重心到一个顶点的距离,等于
它到这个顶点对边中点的距离的两倍.
结合图形,写出这个定理的符号语言.
∵G是△ABC的重心,
∴
或
或
等
2K
K
2a
a
2b
b
补充例题
已知在Rt△ABC中,∠C=90°,中线AD、BE相交于点M,AC=8,BC=6.求CM的长.
分解得到基本图形
延长CM交AB于点F.
在Rt△ABC中,∠C=90°,
∵AC=8,BC=6,
∴AB=
=10
解:∵中线AD、BE相交于点M,
∴点M是△ABC的重心,
∴CF是AB上的中线,
∴CF=
AB=5.
∴CM=
CF=
F
点M是什么特殊点?
课堂练习
1.已知AD、BE是△ABC的中线,AD、BE相交于点F,AD=6,则AF=
,DF=
.
4
2
2.如图已知小明的身高是1.6米,他在路灯下的影长为2米,小明距路灯灯杆的底部3米,则路灯灯炮距地面的高度是_______米.
怎么解决实际问题?
4
A
B
C
D
E
课堂小结
1.三角形一边的平行线性质定理推论.
平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.
符合语言:
∵DE//BC,
∴
3.三角形重心定理:
三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍
.
2.重心定义:三角形三条中线的交点叫做三角形的重心
D
E
1.已知:如图,在平行四边形ABCD中,E是边AB的中点,点F在BC边上,且CF=3BF,EF与BD相交于点G.求证:DG=5BG.
练习
H
o
2.如图,在△
ABC中,AB3.已知:
在△
ABC中,D是AB中点,过点D的直线交AC于E,交BC的延长线于F,求证:
4.已知:
在△
ABC中,D是AB中点,过点D的直线交AC于E,交BC的延长线于F,求证:
谢
谢
24.3三角形一边的平行线
如图,DE∥BC,写出成比例的式子.
复习引入
E
D
a1
a2
b1
b2
a原
b原
a1
a原
b1
b原
a2
b2
同一线段上的对应线段成比例
或
或
或
或
分析:由上节课学习的三角形一边的平行线性质定理
。比例线段分别在三角形两边所在的直线上,因此,考虑将DE平移到BC边上去
探究新知
如图,点D、E分别在△ABC的边AB、AC上,DE∥BC,
那么
成立吗?为什么?
证明:过点D作DF//AC,交边BC于点F.
又∵
∴四边形DFCE是平行四边形.
∴FC=DE.
∵DF//AC
∴
(三角形一边的平行线性质定理)
∴
由DE∥BC,得
∴
F
这两个比例式成立吗?
那这两个比例式呢?
∵FC=DE,∴
由DF∥AC应选用那一组比例线段?
探究新知
由上题可知
当点D、E分别在△ABC的边BA、CA的延长线上时,这个结论仍然成立
符合语言:
∵DE//BC,
∴
(三角形一边的平行线性质定理推论).
D
E
平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.
新知运用
例题2
如图,线段BD与CE相交于点A,ED∥BC,已知2BC=3ED,AC=8,求AE的长.
(1)先在图形中标示
8
?
(2)把“2BC=3ED”转化为
由ED∥BC可得
然后计算求解.
解:∵ED//BC,
∴
(三角形一边的平行线
性质定理推论).
由2BC=3ED,得
∴
∵AC=8,
选用适当的比例式
∴
3
16
=
AC
分析:要证明此结论只要证明EF//BC.
因此想到构造中位线,从而连接EF
新知运用
例题3
已知:如图,BE,CF是△ABC的中线,交于点G.
求证:
证明:联结EF.
∵BE、CF是△ABC的中线,
即
∵EF//BC,∴
即
由两个中点能想到什么?
∴E、F分别是AB、AC中点
∵
(三角形一边的平行线
性质定理推论).
新知运用
如果把原图中CF去掉,BE仍是△ABC的中线,过A作中线交BE于G,问:点G与点G’在不在同一点上?
证明:联结DE,
可得
又点G与点G’同在中线BE上,所以点G与点G’是同一个点.
即
三角形的三条中线交于一点.
三角形三条中线的交点叫做三角形的重心.
G’
三角形重心定理:
三角形的重心到一个顶点的距离,等于
它到这个顶点对边中点的距离的两倍.
结合图形,写出这个定理的符号语言.
∵G是△ABC的重心,
∴
或
或
等
2K
K
2a
a
2b
b
补充例题
已知在Rt△ABC中,∠C=90°,中线AD、BE相交于点M,AC=8,BC=6.求CM的长.
分解得到基本图形
延长CM交AB于点F.
在Rt△ABC中,∠C=90°,
∵AC=8,BC=6,
∴AB=
=10
解:∵中线AD、BE相交于点M,
∴点M是△ABC的重心,
∴CF是AB上的中线,
∴CF=
AB=5.
∴CM=
CF=
F
点M是什么特殊点?
课堂练习
1.已知AD、BE是△ABC的中线,AD、BE相交于点F,AD=6,则AF=
,DF=
.
4
2
2.如图已知小明的身高是1.6米,他在路灯下的影长为2米,小明距路灯灯杆的底部3米,则路灯灯炮距地面的高度是_______米.
怎么解决实际问题?
4
A
B
C
D
E
课堂小结
1.三角形一边的平行线性质定理推论.
平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.
符合语言:
∵DE//BC,
∴
3.三角形重心定理:
三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍
.
2.重心定义:三角形三条中线的交点叫做三角形的重心
D
E
1.已知:如图,在平行四边形ABCD中,E是边AB的中点,点F在BC边上,且CF=3BF,EF与BD相交于点G.求证:DG=5BG.
练习
H
o
2.如图,在△
ABC中,AB
在△
ABC中,D是AB中点,过点D的直线交AC于E,交BC的延长线于F,求证:
4.已知:
在△
ABC中,D是AB中点,过点D的直线交AC于E,交BC的延长线于F,求证:
谢
谢
