高中数学人教B版选修2-1 第二章2.3.2 双曲线的几何性质 课件(共18张PPT)
文档属性
| 名称 | 高中数学人教B版选修2-1 第二章2.3.2 双曲线的几何性质 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 900.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 11:45:36 | ||
图片预览





文档简介
(共18张PPT)
旧知回顾
1、椭圆有哪些几何性质?
2、双曲线的两种标准方程是什么?
焦点在
轴:
焦点在
轴:
新知探究
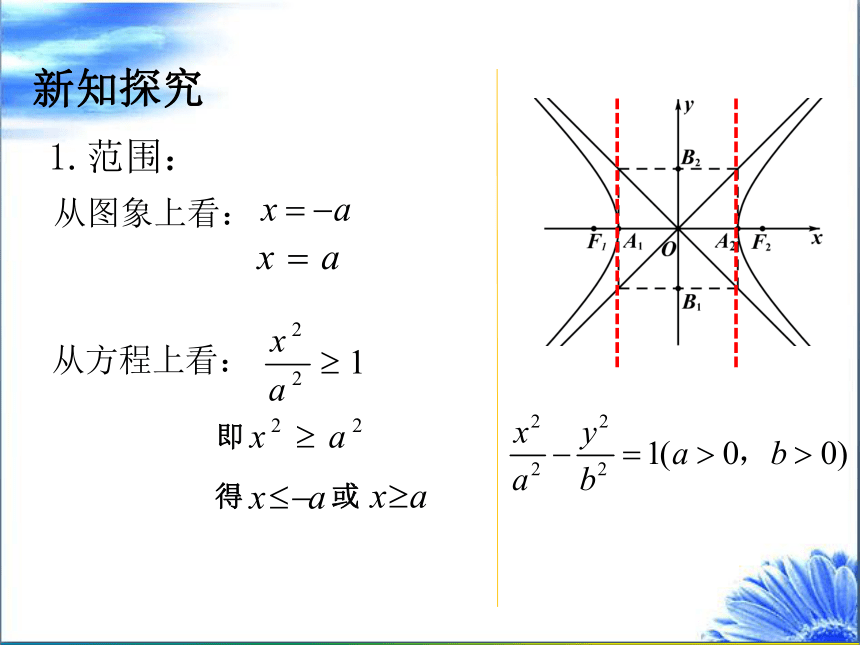
1.范围:
从图象上看:
从方程上看:
即
得
或
2.对称性:
新知探究
从图象上看:
从方程上看:
双曲线关于
轴、
轴、
原点对称.
(1)把
换成
方程不变,图象关于
轴对称;
(2)把
换成
方程不变,图象关于
轴对称;
(3)把
换成
,
换成
方程不变,图象关于原点对称.
原点
对称中心
轴、轴
对称轴
双曲线的中心
新知探究
3.顶点:
从图象上看:
双曲线和它对称轴的两个交点叫做双曲线的顶点.
从方程上看:
令
,则
;
令
,则
;
方程没有实数根.
双曲线的顶点为
新知探究
4.轴:
线段
叫做双曲线的实轴,
且
;
线段
叫做双曲线的虚轴,
且
;
相应的,,分别是双曲线的实半轴长和虚半轴长.
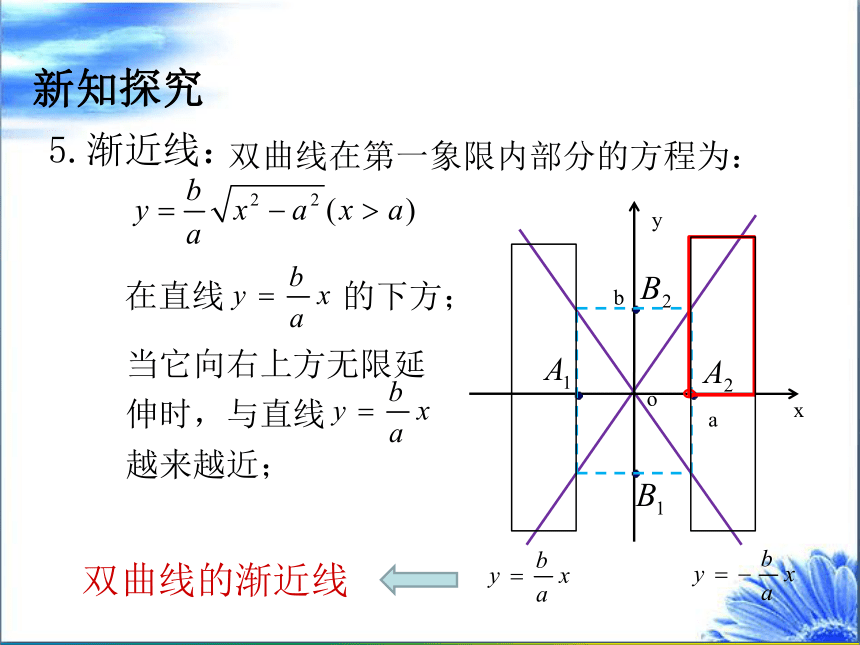
5.渐近线:
新知探究
双曲线在第一象限内部分的方程为:
x
y
o
a
b
在直线
的下方;
当它向右上方无限延伸时,与直线
越来越近;
双曲线的渐近线
新知探究
6.离心率:
双曲线的焦距与实轴的比
叫做双曲线的离心率
注:
1.双曲线的离心率
2.双曲线的离心率可以刻画双曲线的“开口”
离心率越大,开口越大;
离心率越小,开口越小.
显然
知识梳理
典例分析
解:原方程可化为
即
该双曲线的实半轴长为
,虚半轴长为
,
焦点坐标为
,离心率为
,渐
近线方程为
.
典例分析
解:
两点间的距离为8
离心率为
该双曲线的标准方程为
等轴双曲线
典例分析
A
典例分析
解:
双曲线
的渐近线方程为
双曲线
的渐近线方程为
与双曲线
共渐近线的双曲线方程:
典例分析
解:
设所求双曲线的方程为
将
代入到方程,即
整理得
即所求双曲线的方程为
与双曲线
共渐近线的双曲线方程:
典例分析
典例分析
作业
小结
旧知回顾
1、椭圆有哪些几何性质?
2、双曲线的两种标准方程是什么?
焦点在
轴:
焦点在
轴:
新知探究
1.范围:
从图象上看:
从方程上看:
即
得
或
2.对称性:
新知探究
从图象上看:
从方程上看:
双曲线关于
轴、
轴、
原点对称.
(1)把
换成
方程不变,图象关于
轴对称;
(2)把
换成
方程不变,图象关于
轴对称;
(3)把
换成
,
换成
方程不变,图象关于原点对称.
原点
对称中心
轴、轴
对称轴
双曲线的中心
新知探究
3.顶点:
从图象上看:
双曲线和它对称轴的两个交点叫做双曲线的顶点.
从方程上看:
令
,则
;
令
,则
;
方程没有实数根.
双曲线的顶点为
新知探究
4.轴:
线段
叫做双曲线的实轴,
且
;
线段
叫做双曲线的虚轴,
且
;
相应的,,分别是双曲线的实半轴长和虚半轴长.
5.渐近线:
新知探究
双曲线在第一象限内部分的方程为:
x
y
o
a
b
在直线
的下方;
当它向右上方无限延伸时,与直线
越来越近;
双曲线的渐近线
新知探究
6.离心率:
双曲线的焦距与实轴的比
叫做双曲线的离心率
注:
1.双曲线的离心率
2.双曲线的离心率可以刻画双曲线的“开口”
离心率越大,开口越大;
离心率越小,开口越小.
显然
知识梳理
典例分析
解:原方程可化为
即
该双曲线的实半轴长为
,虚半轴长为
,
焦点坐标为
,离心率为
,渐
近线方程为
.
典例分析
解:
两点间的距离为8
离心率为
该双曲线的标准方程为
等轴双曲线
典例分析
A
典例分析
解:
双曲线
的渐近线方程为
双曲线
的渐近线方程为
与双曲线
共渐近线的双曲线方程:
典例分析
解:
设所求双曲线的方程为
将
代入到方程,即
整理得
即所求双曲线的方程为
与双曲线
共渐近线的双曲线方程:
典例分析
典例分析
作业
小结
