人教版数学七年级上册 3.2 课时1 解一元一次方程—合并同类项 课件(24张ppt)
文档属性
| 名称 | 人教版数学七年级上册 3.2 课时1 解一元一次方程—合并同类项 课件(24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-15 06:29:49 | ||
图片预览








文档简介
第三章 一元一次方程
3.2 解一元一次方程(一)—合并同类项与移项
课时1 解一元一次方程—合并同类项
1.会利用合并同类项的方法解一元一次方程,体会等式变形中的化归思想.(重点)
2.能够从实际问题中列出一元一次方程,进一步体会方程模型思想的作用及应用价值.
学习目标
新课导入
知识回顾
(1) 含有相同的_____,并且相同字母的_____也相同的项,叫做同类项;
(2) 合并同类项时,把各同类项的_____相加减,字母和字母的指数_____.
字母
指数
系数
不变
新课导入
约公元820年,数学家阿尔—花拉子米写了一本代数书,重点论述怎样解方程,这本书的拉丁译本为《对消与还原》.“对消”与“还原”是什么意思呢?
情境导入
新课讲解
知识点1 解一元一次方程—合并同类项
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
方法一:
设前年这个学校购买了计算机x台,则去年购买计算机 2x台,今年购买计算机4x台.
前年购买量+去年购买量+今年购买量=140台
根据题意,列得方程
x+2x+4x=140.
新课讲解
还有不同的设法吗?
还可以列怎样的方程?
方法二:设去年购买x台.
方法三:设今年购买x台.
新课讲解
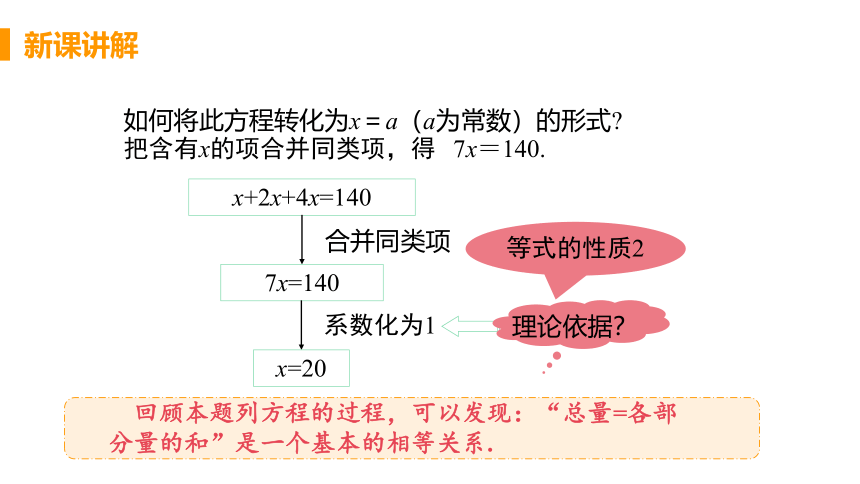
如何将此方程转化为x=a(a为常数)的形式?
把含有x的项合并同类项,得
7x=140.
x+2x+4x=140
合并同类项
系数化为1
等式的性质2
理论依据?
7x=140
x=20
回顾本题列方程的过程,可以发现:“总量=各部分量的和”是一个基本的相等关系.
新课讲解
思考
在解方程过程中,合并同类项起了什么作用?
合并同类项的目的就是化简方程,它是一种恒等变形,可以使方程变得简单,并逐步使方程向x=a的形式转化.
新课讲解
例
典例分析
1. 解下列方程:
解:合并同类项,得
系数化为1,得 x = 4
(1)
新课讲解
典例分析
(2)7x-2.5x+3x-1.5x=-15×4-6×3
解:合并同类项,得
6x = -78
系数化为1,得 x = -13
新课讲解
例
典例分析
2. 有一列数,按一定规律排列成1,-3,9,-27,81,-243,···.其中某三个相邻数的和是-1 701,这三个数各是多少?
分析:从符号和绝对值两方面观察,可发现这列数的排列规律:后面的数是它前面的数与-3的乘积.如果三个相邻数中的第1个记为x,则后两个数分别是-3x,9x.
新课讲解
典例分析
解:设所求三个数分别是x,-3x,9x.
由三个数的和是-1701,得 x - 3x + 9x = -1701.
合并同类项,得 7x = -1701.
系数化为1,得 x = -243.
所以-3x = 729 , 9x= -2187.
答:这三个数是-243,729,-2187.
新课讲解
典例分析
若设所求的三个数中,中间的一个数为x,则它前面的一个数为 ,它后面的一个数为-3x,于是,依题意可列方程
+ x - 3x = -1701.
并求出所列方程的解.
x = 729.
新课讲解
典例分析
若设所求的三个数中第三个数为x,则第一个数为 ,第二个数为 . 依题意可列方程
并求出所列方程的解.
x = -2187
新课讲解
练一练
解下列方程:
解:合并同类项,得
系数化为1,得
(1)5x - 2x = 9
3x = 9
x = 3
解:合并同类项,得
系数化为1,得
新课讲解
练一练
(3)-3x + 0.5x = 10
解:合并同类项,得
-2.5x = 10
系数化为1,得
x = -4
(4)7x - 4.5x = 2.5×3 - 5
解:合并同类项,得
系数化为1,得
2.5x = 2.5
x = 1
课堂小结
x+2x+4x=140
合并同类项
系数化为1
等式的性质2
理论依据?
7x=140
x=20
当堂小练
1.解下列方程:
(1)2x + 3x + 4x = 18
解:合并同类项,得
9x = 18
系数化为1,得
x = 2
(2)13x - 15x + x = -3
解:合并同类项,得
-x = -3
系数化为1,得
x = 3
当堂小练
(3)2.5y + 10y - 6y = 15 - 21.5
解:合并同类项,得
6.5y = - 6.5
系数化为1,得
y = -1
(4)
解:合并同类项,得
系数化为1,得
当堂小练
2. 有一列数:1,-2,4,-8,16,…,若其中三个相邻数的和是312,求这三个数.
解:设这三个数中的第一个数为x,则第二个数为-2x,第三个数为4x.
则由题意,得 x - 2x + 4x = 312.
解得 x = 104.
-2x = -208,4x = 416.
答:这三个数是104,-208,416.
当堂小练
3. 随着农业技术的现代化,节水型灌溉得到了逐步推广,喷灌和滴灌是比漫灌节水的灌溉方式,灌溉三块同样大的实验田,第一块用漫灌方式,第二块用喷灌方式,第三块用滴灌方式,后两种方式用水量分别是漫灌的25%和15%.
(1)设第一块实验田用水x t,则另两块实验田的用水量如何表示?
(2)如果三块实验田共用水420 t,每块实验田各用水多少吨?
当堂小练
解:(1)设第一块实验田用水x t,则第二块实验田用水25%x t,第三块实验田用水15%x t.
(2)由(1)及已知,得
x + 25%x + 15%x = 420.
合并同类项,得 1.4x = 420.
系数化为1,得 x = 300.
所以25%x=75,15%x=45.
即第一块实验田用水300 t,则第二块实验田用水75 t,第三块实验田用水45 t.
D
拓展与延伸
有一列数:6,12,18,24,…,从中取出三个相邻的数.
(1)若这三个相邻的数的和为324,求这三个数.
解:设这三个数中的第一个数为6x,则第二个数为6(x+1),第三个数为6(x+2).
则由题意,得
6x +6( x+1) + 6( x + 2) = 324.
解得 x = 17.
所以6x =102,6( x+1) = 108,6(x + 2) = 114.
即这三个数为102,108,114.
拓展与延伸
有一列数:6,12,18,24,…,从中取出三个相邻的数.
(2)试判断这三个相邻的数的和能否等于84?若能,求出这三个数;若不能,请说明理由.
解:由题意可得第n个数为6n,则第(n-1)个数为6(n-1),第(n+1)个数为6(n+1).则
6(n-1)+6n+6(n+1)=84.
解得n=
因为n为正整数,所以这个解不符题意.
即这三个相邻的数的和不能等于84.
3.2 解一元一次方程(一)—合并同类项与移项
课时1 解一元一次方程—合并同类项
1.会利用合并同类项的方法解一元一次方程,体会等式变形中的化归思想.(重点)
2.能够从实际问题中列出一元一次方程,进一步体会方程模型思想的作用及应用价值.
学习目标
新课导入
知识回顾
(1) 含有相同的_____,并且相同字母的_____也相同的项,叫做同类项;
(2) 合并同类项时,把各同类项的_____相加减,字母和字母的指数_____.
字母
指数
系数
不变
新课导入
约公元820年,数学家阿尔—花拉子米写了一本代数书,重点论述怎样解方程,这本书的拉丁译本为《对消与还原》.“对消”与“还原”是什么意思呢?
情境导入
新课讲解
知识点1 解一元一次方程—合并同类项
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
方法一:
设前年这个学校购买了计算机x台,则去年购买计算机 2x台,今年购买计算机4x台.
前年购买量+去年购买量+今年购买量=140台
根据题意,列得方程
x+2x+4x=140.
新课讲解
还有不同的设法吗?
还可以列怎样的方程?
方法二:设去年购买x台.
方法三:设今年购买x台.
新课讲解
如何将此方程转化为x=a(a为常数)的形式?
把含有x的项合并同类项,得
7x=140.
x+2x+4x=140
合并同类项
系数化为1
等式的性质2
理论依据?
7x=140
x=20
回顾本题列方程的过程,可以发现:“总量=各部分量的和”是一个基本的相等关系.
新课讲解
思考
在解方程过程中,合并同类项起了什么作用?
合并同类项的目的就是化简方程,它是一种恒等变形,可以使方程变得简单,并逐步使方程向x=a的形式转化.
新课讲解
例
典例分析
1. 解下列方程:
解:合并同类项,得
系数化为1,得 x = 4
(1)
新课讲解
典例分析
(2)7x-2.5x+3x-1.5x=-15×4-6×3
解:合并同类项,得
6x = -78
系数化为1,得 x = -13
新课讲解
例
典例分析
2. 有一列数,按一定规律排列成1,-3,9,-27,81,-243,···.其中某三个相邻数的和是-1 701,这三个数各是多少?
分析:从符号和绝对值两方面观察,可发现这列数的排列规律:后面的数是它前面的数与-3的乘积.如果三个相邻数中的第1个记为x,则后两个数分别是-3x,9x.
新课讲解
典例分析
解:设所求三个数分别是x,-3x,9x.
由三个数的和是-1701,得 x - 3x + 9x = -1701.
合并同类项,得 7x = -1701.
系数化为1,得 x = -243.
所以-3x = 729 , 9x= -2187.
答:这三个数是-243,729,-2187.
新课讲解
典例分析
若设所求的三个数中,中间的一个数为x,则它前面的一个数为 ,它后面的一个数为-3x,于是,依题意可列方程
+ x - 3x = -1701.
并求出所列方程的解.
x = 729.
新课讲解
典例分析
若设所求的三个数中第三个数为x,则第一个数为 ,第二个数为 . 依题意可列方程
并求出所列方程的解.
x = -2187
新课讲解
练一练
解下列方程:
解:合并同类项,得
系数化为1,得
(1)5x - 2x = 9
3x = 9
x = 3
解:合并同类项,得
系数化为1,得
新课讲解
练一练
(3)-3x + 0.5x = 10
解:合并同类项,得
-2.5x = 10
系数化为1,得
x = -4
(4)7x - 4.5x = 2.5×3 - 5
解:合并同类项,得
系数化为1,得
2.5x = 2.5
x = 1
课堂小结
x+2x+4x=140
合并同类项
系数化为1
等式的性质2
理论依据?
7x=140
x=20
当堂小练
1.解下列方程:
(1)2x + 3x + 4x = 18
解:合并同类项,得
9x = 18
系数化为1,得
x = 2
(2)13x - 15x + x = -3
解:合并同类项,得
-x = -3
系数化为1,得
x = 3
当堂小练
(3)2.5y + 10y - 6y = 15 - 21.5
解:合并同类项,得
6.5y = - 6.5
系数化为1,得
y = -1
(4)
解:合并同类项,得
系数化为1,得
当堂小练
2. 有一列数:1,-2,4,-8,16,…,若其中三个相邻数的和是312,求这三个数.
解:设这三个数中的第一个数为x,则第二个数为-2x,第三个数为4x.
则由题意,得 x - 2x + 4x = 312.
解得 x = 104.
-2x = -208,4x = 416.
答:这三个数是104,-208,416.
当堂小练
3. 随着农业技术的现代化,节水型灌溉得到了逐步推广,喷灌和滴灌是比漫灌节水的灌溉方式,灌溉三块同样大的实验田,第一块用漫灌方式,第二块用喷灌方式,第三块用滴灌方式,后两种方式用水量分别是漫灌的25%和15%.
(1)设第一块实验田用水x t,则另两块实验田的用水量如何表示?
(2)如果三块实验田共用水420 t,每块实验田各用水多少吨?
当堂小练
解:(1)设第一块实验田用水x t,则第二块实验田用水25%x t,第三块实验田用水15%x t.
(2)由(1)及已知,得
x + 25%x + 15%x = 420.
合并同类项,得 1.4x = 420.
系数化为1,得 x = 300.
所以25%x=75,15%x=45.
即第一块实验田用水300 t,则第二块实验田用水75 t,第三块实验田用水45 t.
D
拓展与延伸
有一列数:6,12,18,24,…,从中取出三个相邻的数.
(1)若这三个相邻的数的和为324,求这三个数.
解:设这三个数中的第一个数为6x,则第二个数为6(x+1),第三个数为6(x+2).
则由题意,得
6x +6( x+1) + 6( x + 2) = 324.
解得 x = 17.
所以6x =102,6( x+1) = 108,6(x + 2) = 114.
即这三个数为102,108,114.
拓展与延伸
有一列数:6,12,18,24,…,从中取出三个相邻的数.
(2)试判断这三个相邻的数的和能否等于84?若能,求出这三个数;若不能,请说明理由.
解:由题意可得第n个数为6n,则第(n-1)个数为6(n-1),第(n+1)个数为6(n+1).则
6(n-1)+6n+6(n+1)=84.
解得n=
因为n为正整数,所以这个解不符题意.
即这三个相邻的数的和不能等于84.
