人教版数学七年级上册 3.3 课时2解一元一次方程—去分母 课件(21张ppt)
文档属性
| 名称 | 人教版数学七年级上册 3.3 课时2解一元一次方程—去分母 课件(21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 265.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-15 00:00:00 | ||
图片预览








文档简介
第三章 一元一次方程
3.3 解一元一次方程(二)—去括号与去分母
课时2 解一元一次方程—去分母
1.掌握去分母解方程的方法,总结解方程的步骤.(重点)
2.经历去分母解方程的过程,体会把“复杂”转化为
“简单”,把“新”转化为“旧”的转化的思想方
法.(难点)
学习目标
新课导入
丢番图的墓志铭
“坟中安葬着丢番图,多么令人惊讶,它忠实地记录了所经历的道路.上帝给予的童年占六分之一.又过十二分之一,两颊长胡.再过七分之一,点燃结婚的蜡烛.五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓.悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途.”
你知道丢番图去世时的年龄吗?你认为本题用算术方法解方便,还是用方程方法解方便?
解:设丢番图活了x岁,根据题意,得
新课导入
你能解出这道方程吗?把你的解法与其他同学交流一下,看谁的解法好.
像上面这样的方程中有些系数是分数,如果能化去分母,把系数化为整数,则可以使解方程中的计算更方便些.
结论
新课讲解
知识点1 解一元一次方程—去分母
一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,求这个数.
分析:设这个数为x.
根据题意,得
新课讲解
方法1:合并同类项,得
系数化为1,得
新课讲解
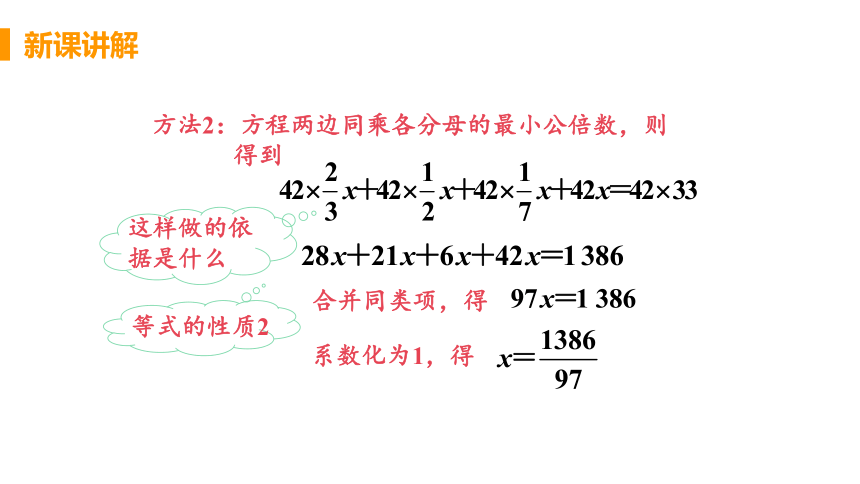
方法2:方程两边同乘各分母的最小公倍数,则
得到
合并同类项,得
系数化为1,得
这样做的依据是什么
等式的性质2
新课讲解
为了更全面的讨论问题,我们再以以下的方程为例。
方程两边乘10,
下面的框图表示解这个方程的流程.
新课讲解
5(3x+1)– 10×2=(3x – 2)– 2(2x+3)
15x + 5 – 20 = 3x – 2 – 4x – 6
15x – 3x + 4x = – 2 – 6 – 5+20
16x = 7
去分母(方程两边乘各分母的最小公倍数)
去括号
移项
合并同类项
系数化为1
新课讲解
结论
解一元一次方程的一般步骤包括:去分母、去括号、移项、合并同类项、系数化为1等. 通过这些步骤可以使以x为未知数的方程逐步向着x=a的形式转化,这个过程主要依据等式的基本性质和运算律等.
新课讲解
例
典例分析
1. 解下列方程:
解:去分母(方程两边乘4),得
2(x + 1) – 4 = 8 +(2 – x).
去括号,得 2x + 2 – 4 = 8 + 2 – x.
移项,得 2x + x = 8 + 2 – 2 + 4 .
合并同类项,得 3x = 12.
系数化为1,得 x = 4.
新课讲解
典例分析
解:去分母(方程两边乘6),得
18x + 3(x – 1)= 18 – 2(2x – 1)
去括号,得 18x + 3x – 3 = 18 – 4x + 2
移项,得 18x + 3x +4x = 18 + 2 + 3
合并同类项,得 25x = 23
系数化为1,得
新课讲解
练一练
解:去分母(方程两边乘100),得
19x = 21(x – 2).
去括号,得 19x = 21x – 42.
移项,得 19x – 21x = – 42.
合并同类项,得 – 2x = – 42.
系数化为1,得 x = 21.
解下列方程:
新课讲解
练一练
解下列方程:
解:去分母(方程两边乘4),得
2(x + 1)– 8 = x.
去括号,得 2x + 2 – 8 = x .
移项,得 2x – x =8 – 2
合并同类项,得 x = 6.
新课讲解
练一练
解下列方程:
解:去分母(方程两边乘12),得
3(5x – 1) = 6(3x + 1)– 4(2 – x)
去括号,得 15x – 3 = 18x + 6– 8 + 4x
移项,得 15x – 18x – 4x = 6 – 8 + 3
合并同类项,得 – 7x = 1
系数化为1,得
新课讲解
练一练
某中学组织团员到校外参加义务植树活动,一部分团员骑自行车先走,速度为 9 km/h,40分钟后其余团员乘汽车出发,速度为 45 km/h,结果他们同时到达目的地,则目的地距学校多少千米?
解:设目的地距学校x km,则骑自行车所用时间为 h,乘汽车所用时间为 h.
由题意,得 解得 x=7.5.
答:目的地距学校7.5 km.
课堂小结
解一元一次方程的一般步骤:
变形名称
具体的做法与依据
去分母
乘所有的分母的最小公倍数.
依据是等式性质2.
去括号
先去小括号,再去中括号,最后去大括号.
依据是去括号法则和乘法分配律.
移项
把含有未知数的项移到一边,常数项移到另一边.“过桥变号”,依据是等式性质1.
合并同类项
将未知数的系数相加,常数项相加.
依据是合并同类项法则.
系数化为1
在方程的两边除以未知数的系数.
依据是等式性质2.
当堂小练
1. 解方程 时,去分母正确的是( )
A. 3x-1 = 2(x-1)
B. 3x-6 = 2(x-1)
C. 3x-6 = 2x-1
D. 3x-3 = 2x-1
B
当堂小练
2. 解方程:
解:第一步________,得10 – 2(x + 2) = 5(x – 1).
第二步________,得10 –2x – 4 = 5x – 5.
第三步______,得 – 2x – 5x = –5 –10 + 4.
第四步____________,得 – 7x = –11.
第五步____________,得 x = .
去分母
去括号
移项
合并同类项
系数化为1
当堂小练
3. 列方程解答下面问题. y的3倍与1.5的和的二分之一等于y与1的差的四分之一,求y.
解:根据题意,得
解得
D
拓展与延伸
有一些相同的房间需要粉刷墙面,一天3名一级技工去粉刷8个房间,结果其中有50 m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40 m2墙面,每名一级技工比二级技工一天多粉刷10 m2墙面,求每个房间需要粉刷的墙面面积.
解:设每个房间需要粉刷的墙面面积为x m2.
解得 x = 52
答:每个房间需要粉刷的墙面面积为52 m2.
则
3.3 解一元一次方程(二)—去括号与去分母
课时2 解一元一次方程—去分母
1.掌握去分母解方程的方法,总结解方程的步骤.(重点)
2.经历去分母解方程的过程,体会把“复杂”转化为
“简单”,把“新”转化为“旧”的转化的思想方
法.(难点)
学习目标
新课导入
丢番图的墓志铭
“坟中安葬着丢番图,多么令人惊讶,它忠实地记录了所经历的道路.上帝给予的童年占六分之一.又过十二分之一,两颊长胡.再过七分之一,点燃结婚的蜡烛.五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓.悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途.”
你知道丢番图去世时的年龄吗?你认为本题用算术方法解方便,还是用方程方法解方便?
解:设丢番图活了x岁,根据题意,得
新课导入
你能解出这道方程吗?把你的解法与其他同学交流一下,看谁的解法好.
像上面这样的方程中有些系数是分数,如果能化去分母,把系数化为整数,则可以使解方程中的计算更方便些.
结论
新课讲解
知识点1 解一元一次方程—去分母
一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,求这个数.
分析:设这个数为x.
根据题意,得
新课讲解
方法1:合并同类项,得
系数化为1,得
新课讲解
方法2:方程两边同乘各分母的最小公倍数,则
得到
合并同类项,得
系数化为1,得
这样做的依据是什么
等式的性质2
新课讲解
为了更全面的讨论问题,我们再以以下的方程为例。
方程两边乘10,
下面的框图表示解这个方程的流程.
新课讲解
5(3x+1)– 10×2=(3x – 2)– 2(2x+3)
15x + 5 – 20 = 3x – 2 – 4x – 6
15x – 3x + 4x = – 2 – 6 – 5+20
16x = 7
去分母(方程两边乘各分母的最小公倍数)
去括号
移项
合并同类项
系数化为1
新课讲解
结论
解一元一次方程的一般步骤包括:去分母、去括号、移项、合并同类项、系数化为1等. 通过这些步骤可以使以x为未知数的方程逐步向着x=a的形式转化,这个过程主要依据等式的基本性质和运算律等.
新课讲解
例
典例分析
1. 解下列方程:
解:去分母(方程两边乘4),得
2(x + 1) – 4 = 8 +(2 – x).
去括号,得 2x + 2 – 4 = 8 + 2 – x.
移项,得 2x + x = 8 + 2 – 2 + 4 .
合并同类项,得 3x = 12.
系数化为1,得 x = 4.
新课讲解
典例分析
解:去分母(方程两边乘6),得
18x + 3(x – 1)= 18 – 2(2x – 1)
去括号,得 18x + 3x – 3 = 18 – 4x + 2
移项,得 18x + 3x +4x = 18 + 2 + 3
合并同类项,得 25x = 23
系数化为1,得
新课讲解
练一练
解:去分母(方程两边乘100),得
19x = 21(x – 2).
去括号,得 19x = 21x – 42.
移项,得 19x – 21x = – 42.
合并同类项,得 – 2x = – 42.
系数化为1,得 x = 21.
解下列方程:
新课讲解
练一练
解下列方程:
解:去分母(方程两边乘4),得
2(x + 1)– 8 = x.
去括号,得 2x + 2 – 8 = x .
移项,得 2x – x =8 – 2
合并同类项,得 x = 6.
新课讲解
练一练
解下列方程:
解:去分母(方程两边乘12),得
3(5x – 1) = 6(3x + 1)– 4(2 – x)
去括号,得 15x – 3 = 18x + 6– 8 + 4x
移项,得 15x – 18x – 4x = 6 – 8 + 3
合并同类项,得 – 7x = 1
系数化为1,得
新课讲解
练一练
某中学组织团员到校外参加义务植树活动,一部分团员骑自行车先走,速度为 9 km/h,40分钟后其余团员乘汽车出发,速度为 45 km/h,结果他们同时到达目的地,则目的地距学校多少千米?
解:设目的地距学校x km,则骑自行车所用时间为 h,乘汽车所用时间为 h.
由题意,得 解得 x=7.5.
答:目的地距学校7.5 km.
课堂小结
解一元一次方程的一般步骤:
变形名称
具体的做法与依据
去分母
乘所有的分母的最小公倍数.
依据是等式性质2.
去括号
先去小括号,再去中括号,最后去大括号.
依据是去括号法则和乘法分配律.
移项
把含有未知数的项移到一边,常数项移到另一边.“过桥变号”,依据是等式性质1.
合并同类项
将未知数的系数相加,常数项相加.
依据是合并同类项法则.
系数化为1
在方程的两边除以未知数的系数.
依据是等式性质2.
当堂小练
1. 解方程 时,去分母正确的是( )
A. 3x-1 = 2(x-1)
B. 3x-6 = 2(x-1)
C. 3x-6 = 2x-1
D. 3x-3 = 2x-1
B
当堂小练
2. 解方程:
解:第一步________,得10 – 2(x + 2) = 5(x – 1).
第二步________,得10 –2x – 4 = 5x – 5.
第三步______,得 – 2x – 5x = –5 –10 + 4.
第四步____________,得 – 7x = –11.
第五步____________,得 x = .
去分母
去括号
移项
合并同类项
系数化为1
当堂小练
3. 列方程解答下面问题. y的3倍与1.5的和的二分之一等于y与1的差的四分之一,求y.
解:根据题意,得
解得
D
拓展与延伸
有一些相同的房间需要粉刷墙面,一天3名一级技工去粉刷8个房间,结果其中有50 m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40 m2墙面,每名一级技工比二级技工一天多粉刷10 m2墙面,求每个房间需要粉刷的墙面面积.
解:设每个房间需要粉刷的墙面面积为x m2.
解得 x = 52
答:每个房间需要粉刷的墙面面积为52 m2.
则
