人教版数学九年级上册24.1.4 圆周角 说课课件(共21张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.1.4 圆周角 说课课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-16 14:41:03 | ||
图片预览







文档简介
(共21张PPT)
24.1.4圆周角
题目:
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交于⊙O点D,求BC,AD,BD的长.
九年级上册
87页
24.1.4圆周角
例4
说题流程
一、审题分析
二、解题过程
三、总结提升
四、评价分析
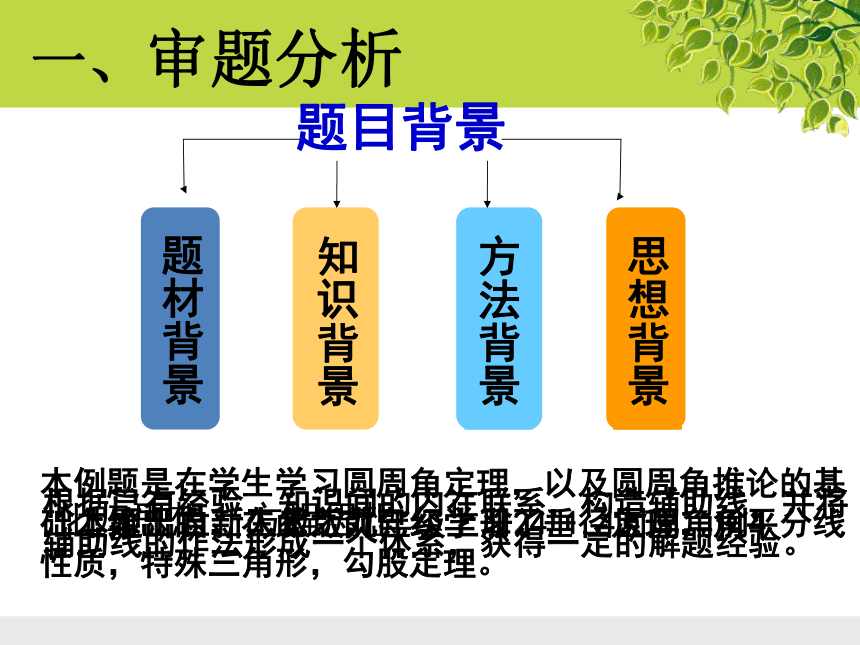
一、审题分析
题目背景
题材背景
知识背景
思想背景
方法背景
本题出自新人教版九年级上册24.1.4圆周角例4
本例题是在学生学习圆周角定理,以及圆周角推论的基础上给出的,在此之前已经学习了垂径定理,角平分线性质,特殊三角形,勾股定理。
根据已有经验,知识间的内在联系,构造辅助线,并将辅助线的作法形成一个体系,获得一定的解题经验。
化归思想、方程思想
一、审题分析---
学情分析
学生特点:本题的教学对象是毕业班学生,他们的观察能力
有所发展,抽象逻辑思维开始占优势,具有了从一定问题中
抽象概括出一般规律的能力。
策略:从多个角度观察图形,寻找弦、弧、角的多重身份,联想它们的性质定理以及对应的基本图形,再结合已有的图形,进行比较,寻找差异,尝试构造性质定理所对应的基本图形,
引导学生体会数学知识之间的联系,感受数学的整体性,不断丰富解决问题的策略,提高解决问题的能力。
估计学生会出现的困难:
1.学生刚接触圆,对各性质定理的理解还不深入,各元素的联系与转换尚不熟悉,看问题比较片面与孤立;
2.本题综合性强,跨度大,关系多,能力要求高,学生还缺乏全局统筹的经验,不容易协调。
《课程标准》要求
一、审题分析---重、难点
难点
利用圆周角定理的推论,同圆中
弧、弦之间的关系以及勾股定理
解决问题。
重点
图形中元素之间的联系与转换,位置与数量关系的处理,典型辅助线的联想、添加以及运用。
一、审题分析---教材编写意图
本题是对前面的垂径定理,圆周角定理,弦、弧、圆心角定理的巩固与深化,对相关知识与思想方法应用的示范。
二、解题过程---问题导思
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD的长.
请学生观察图形,分析已知条件,回答下列问题:
1.所求线段BC,AD,BD对于圆来说是什么身份,计算弦长有什么方法?
2.线段BC,AD,BD关于三角形又是什么身份,三角形边长怎么求?
3.BC所在的三角形有特殊性吗?什么特殊性?AD,BD所在的三角形呢?
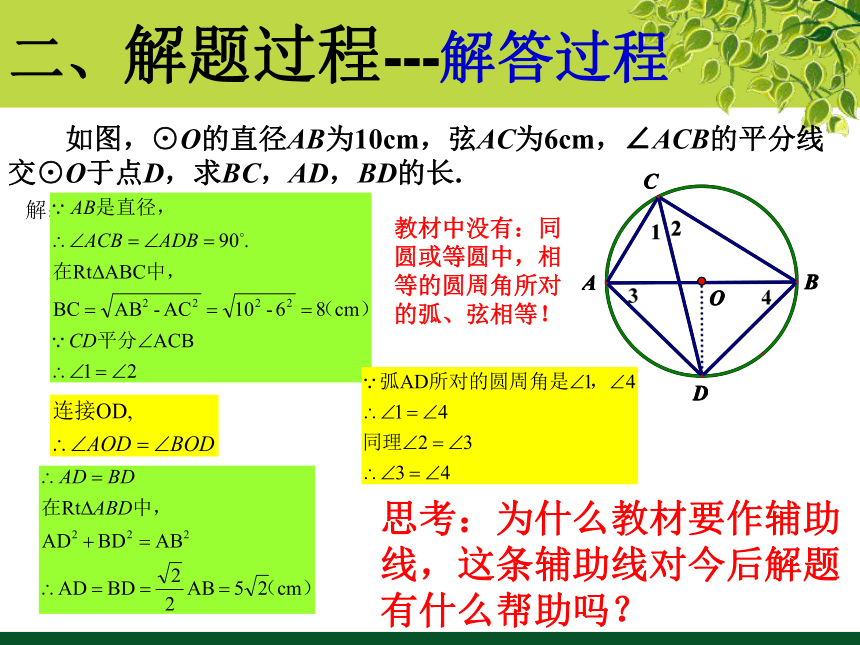
二、解题过程---解答过程
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD的长.
解:
思考:为什么教材要作辅助线,这条辅助线对今后解题有什么帮助吗?
教材中没有:同圆或等圆中,相等的圆周角所对的弧、弦相等!
三、总结提升---提炼模型
在
中,
角平分线
圆周角相等
圆心角相等
弦、弧相等
思路
辅助线出现
等弧、半径
垂径定理
连接OC
三、总结提升---模型应用
求证:∠MAO=∠MAD.
1.已知:如图15,△ABC
内接于⊙O,AM
平分
∠BAC
交⊙O于点M,AD⊥BC于D.
三、总结提升---模型应用
求证:∠MAO=∠MAD.
1.已知:如图15,△ABC
内接于⊙O,AM
平分
∠BAC
交⊙O于点M,AD⊥BC于D.
AM
平分∠BAC
连接OM,OB,OC
角平分线
圆周角相等
圆心角相等
弦、弧相等
思路
辅助线出现
等弧、半径
垂径定理
连接OC
三、总结提升---模型应用
等弧、半径
垂径定理
连接AO
三、总结提升---模型归纳
在
中,
角平分线
圆周角相等
圆心角相等
弦、弧相等
思路
辅助线出现
等弧、半径
垂径定理
连接OC
等腰三角形
直角三角形
三、总结提升---题目变式延伸
原题已求出除CD以外的所有的弦长,这不得不引起我们的思考:CD的长可以求出来吗?
构造等腰三角形
构造直角三角形
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD,CD的长.
三、总结提升---题目变式延伸
原题可求出除CD以外的所有弦长,这不得不引起我们的思考:CD的长可以求出来吗?
1
2
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD,CD的长.
三、总结提升---题目变式延伸
原题可求出除CD以外的所有弦长,这不得不引起我们的思考:CD的长可以求出来吗?
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD,CD的长.
三、总结提升---题目变式延伸
原题可求出除CD以外的所有弦长,这不得不引起我们的思考:CD的长可以求出来吗?
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD,CD的长.
常见解法
等腰直角三角形
角平分线、四边形
常见思路,但没有充分运用特殊角的条件
充分利用特殊角构造等腰直角三角形
从角平分线入手,构造角平分线基本图形,再由特殊角得到特殊四边形
三、总结提升---解题方法总结
四、评价分析---教学反思
1.建构基本模型
学习圆,学生最怕的就是综合证明题,尤其是圆与特殊三角形、特殊四边形的结合。等量关系多,转换方式巧妙,对学生挑战很大,因此要求学生对所学过的基本模型要扎实记忆,灵活运用,要求教师要对新出现的几何图形,引导学生构建基本模型,从而形成体系。
2.辅助线的作法、应用
关于圆的几何题辅助线之多,构造之巧妙,对学生来说也是一大障碍,这就要求教师引导学生思考每一条辅助线的由来,为什么要作,怎么作。
3.我的疑惑
教材中没有“在同圆或等圆中,相等的圆周角所对的弧、弦相等”,但我们可以推导出这句话是正确的,因此我存在一个疑惑:为什么教材不把这句话直接作为性质使用,在书写过程中需要将这个推导过程写完整吗?借此机会希望各位同行答疑解惑!
谢谢!
24.1.4圆周角
题目:
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交于⊙O点D,求BC,AD,BD的长.
九年级上册
87页
24.1.4圆周角
例4
说题流程
一、审题分析
二、解题过程
三、总结提升
四、评价分析
一、审题分析
题目背景
题材背景
知识背景
思想背景
方法背景
本题出自新人教版九年级上册24.1.4圆周角例4
本例题是在学生学习圆周角定理,以及圆周角推论的基础上给出的,在此之前已经学习了垂径定理,角平分线性质,特殊三角形,勾股定理。
根据已有经验,知识间的内在联系,构造辅助线,并将辅助线的作法形成一个体系,获得一定的解题经验。
化归思想、方程思想
一、审题分析---
学情分析
学生特点:本题的教学对象是毕业班学生,他们的观察能力
有所发展,抽象逻辑思维开始占优势,具有了从一定问题中
抽象概括出一般规律的能力。
策略:从多个角度观察图形,寻找弦、弧、角的多重身份,联想它们的性质定理以及对应的基本图形,再结合已有的图形,进行比较,寻找差异,尝试构造性质定理所对应的基本图形,
引导学生体会数学知识之间的联系,感受数学的整体性,不断丰富解决问题的策略,提高解决问题的能力。
估计学生会出现的困难:
1.学生刚接触圆,对各性质定理的理解还不深入,各元素的联系与转换尚不熟悉,看问题比较片面与孤立;
2.本题综合性强,跨度大,关系多,能力要求高,学生还缺乏全局统筹的经验,不容易协调。
《课程标准》要求
一、审题分析---重、难点
难点
利用圆周角定理的推论,同圆中
弧、弦之间的关系以及勾股定理
解决问题。
重点
图形中元素之间的联系与转换,位置与数量关系的处理,典型辅助线的联想、添加以及运用。
一、审题分析---教材编写意图
本题是对前面的垂径定理,圆周角定理,弦、弧、圆心角定理的巩固与深化,对相关知识与思想方法应用的示范。
二、解题过程---问题导思
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD的长.
请学生观察图形,分析已知条件,回答下列问题:
1.所求线段BC,AD,BD对于圆来说是什么身份,计算弦长有什么方法?
2.线段BC,AD,BD关于三角形又是什么身份,三角形边长怎么求?
3.BC所在的三角形有特殊性吗?什么特殊性?AD,BD所在的三角形呢?
二、解题过程---解答过程
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD的长.
解:
思考:为什么教材要作辅助线,这条辅助线对今后解题有什么帮助吗?
教材中没有:同圆或等圆中,相等的圆周角所对的弧、弦相等!
三、总结提升---提炼模型
在
中,
角平分线
圆周角相等
圆心角相等
弦、弧相等
思路
辅助线出现
等弧、半径
垂径定理
连接OC
三、总结提升---模型应用
求证:∠MAO=∠MAD.
1.已知:如图15,△ABC
内接于⊙O,AM
平分
∠BAC
交⊙O于点M,AD⊥BC于D.
三、总结提升---模型应用
求证:∠MAO=∠MAD.
1.已知:如图15,△ABC
内接于⊙O,AM
平分
∠BAC
交⊙O于点M,AD⊥BC于D.
AM
平分∠BAC
连接OM,OB,OC
角平分线
圆周角相等
圆心角相等
弦、弧相等
思路
辅助线出现
等弧、半径
垂径定理
连接OC
三、总结提升---模型应用
等弧、半径
垂径定理
连接AO
三、总结提升---模型归纳
在
中,
角平分线
圆周角相等
圆心角相等
弦、弧相等
思路
辅助线出现
等弧、半径
垂径定理
连接OC
等腰三角形
直角三角形
三、总结提升---题目变式延伸
原题已求出除CD以外的所有的弦长,这不得不引起我们的思考:CD的长可以求出来吗?
构造等腰三角形
构造直角三角形
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD,CD的长.
三、总结提升---题目变式延伸
原题可求出除CD以外的所有弦长,这不得不引起我们的思考:CD的长可以求出来吗?
1
2
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD,CD的长.
三、总结提升---题目变式延伸
原题可求出除CD以外的所有弦长,这不得不引起我们的思考:CD的长可以求出来吗?
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD,CD的长.
三、总结提升---题目变式延伸
原题可求出除CD以外的所有弦长,这不得不引起我们的思考:CD的长可以求出来吗?
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD,BD,CD的长.
常见解法
等腰直角三角形
角平分线、四边形
常见思路,但没有充分运用特殊角的条件
充分利用特殊角构造等腰直角三角形
从角平分线入手,构造角平分线基本图形,再由特殊角得到特殊四边形
三、总结提升---解题方法总结
四、评价分析---教学反思
1.建构基本模型
学习圆,学生最怕的就是综合证明题,尤其是圆与特殊三角形、特殊四边形的结合。等量关系多,转换方式巧妙,对学生挑战很大,因此要求学生对所学过的基本模型要扎实记忆,灵活运用,要求教师要对新出现的几何图形,引导学生构建基本模型,从而形成体系。
2.辅助线的作法、应用
关于圆的几何题辅助线之多,构造之巧妙,对学生来说也是一大障碍,这就要求教师引导学生思考每一条辅助线的由来,为什么要作,怎么作。
3.我的疑惑
教材中没有“在同圆或等圆中,相等的圆周角所对的弧、弦相等”,但我们可以推导出这句话是正确的,因此我存在一个疑惑:为什么教材不把这句话直接作为性质使用,在书写过程中需要将这个推导过程写完整吗?借此机会希望各位同行答疑解惑!
谢谢!
同课章节目录
