专题09 立体几何 教案(文科专用)(解析版)
文档属性
| 名称 | 专题09 立体几何 教案(文科专用)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 728.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 00:00:00 | ||
图片预览



文档简介
专题09
立体几何
1.【2019年高考全国Ⅱ卷文数】设α,β为两个平面,则α∥β的充要条件是
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面
【答案】B
【解析】由面面平行的判定定理知:内两条相交直线都与平行是的充分条件,由面面平行性质定理知,若,则内任意一条直线都与平行,所以内两条相交直线都与平行是的必要条件,故选B.
【名师点睛】本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用面面平行的判定定理与性质定理即可作出判断.面面平行的判定问题要紧扣面面平行判定定理,最容易犯的错误为定理记不住,凭主观臆断,如:“若,则”此类的错误.
2.【2019年高考全国Ⅲ卷文数】如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则()
A.BM=EN,且直线BM,EN是相交直线
B.BM≠EN,且直线BM,EN是相交直线
C.BM=EN,且直线BM,EN是异面直线
D.BM≠EN,且直线BM,EN是异面直线
【答案】B
【解析】如图所示,作于,连接,BD,易得直线BM,EN
是三角形EBD的中线,是相交直线.过作于,连接,平面平面,平面,平面,平面,与均为直角三角形.设正方形边长为2,易知,,,故选B.
【名师点睛】本题考查空间想象能力和计算能力,解答本题的关键是构造直角三角形.解答本题时,先利用垂直关系,再结合勾股定理进而解决问题.
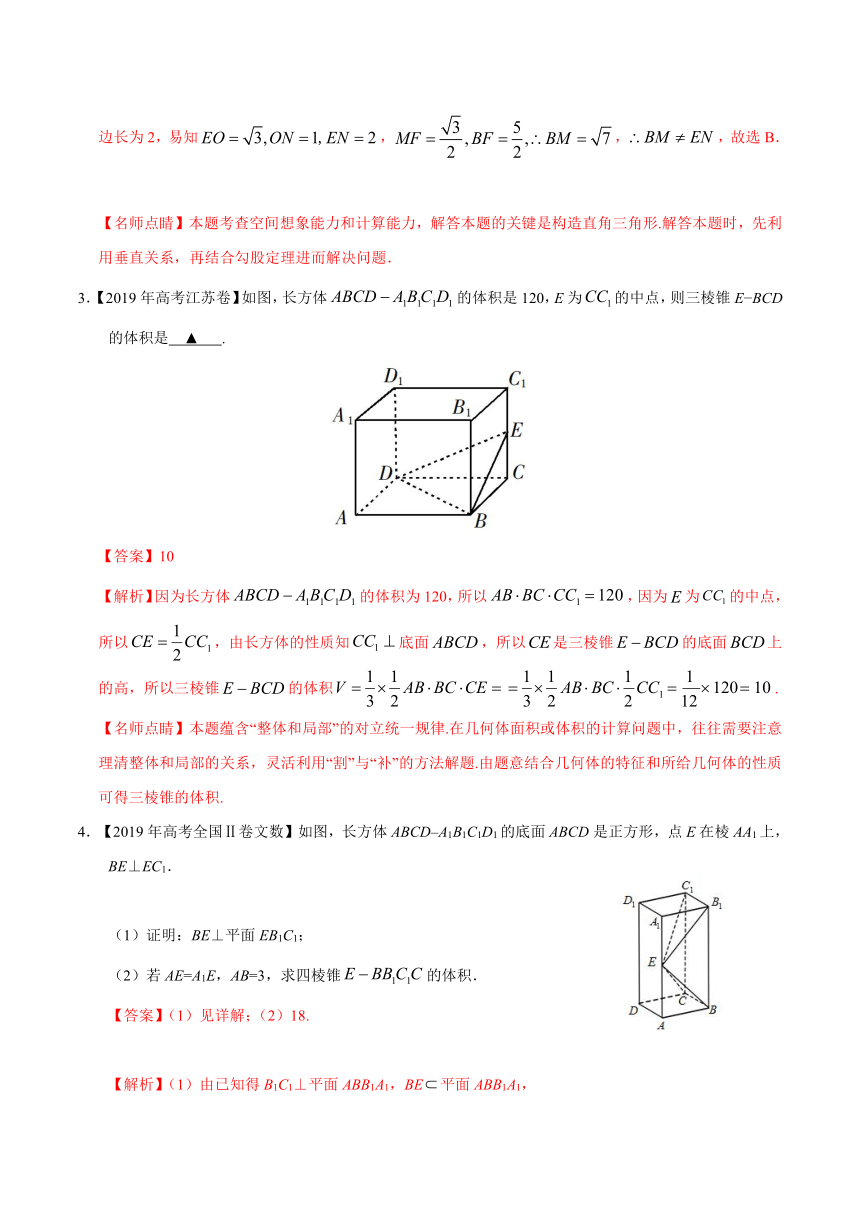
3.【2019年高考江苏卷】如图,长方体的体积是120,E为的中点,则三棱锥E?BCD的体积是
▲
.
【答案】10
【解析】因为长方体的体积为120,所以,因为为的中点,所以,由长方体的性质知底面,所以是三棱锥的底面上的高,所以三棱锥的体积.
【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中,往往需要注意理清整体和局部的关系,灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.
4.【2019年高考全国Ⅱ卷文数】如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,AB=3,求四棱锥的体积.
【答案】(1)见详解;(2)18.
【解析】(1)由已知得B1C1⊥平面ABB1A1,BE平面ABB1A1,
故.又,所以BE⊥平面.
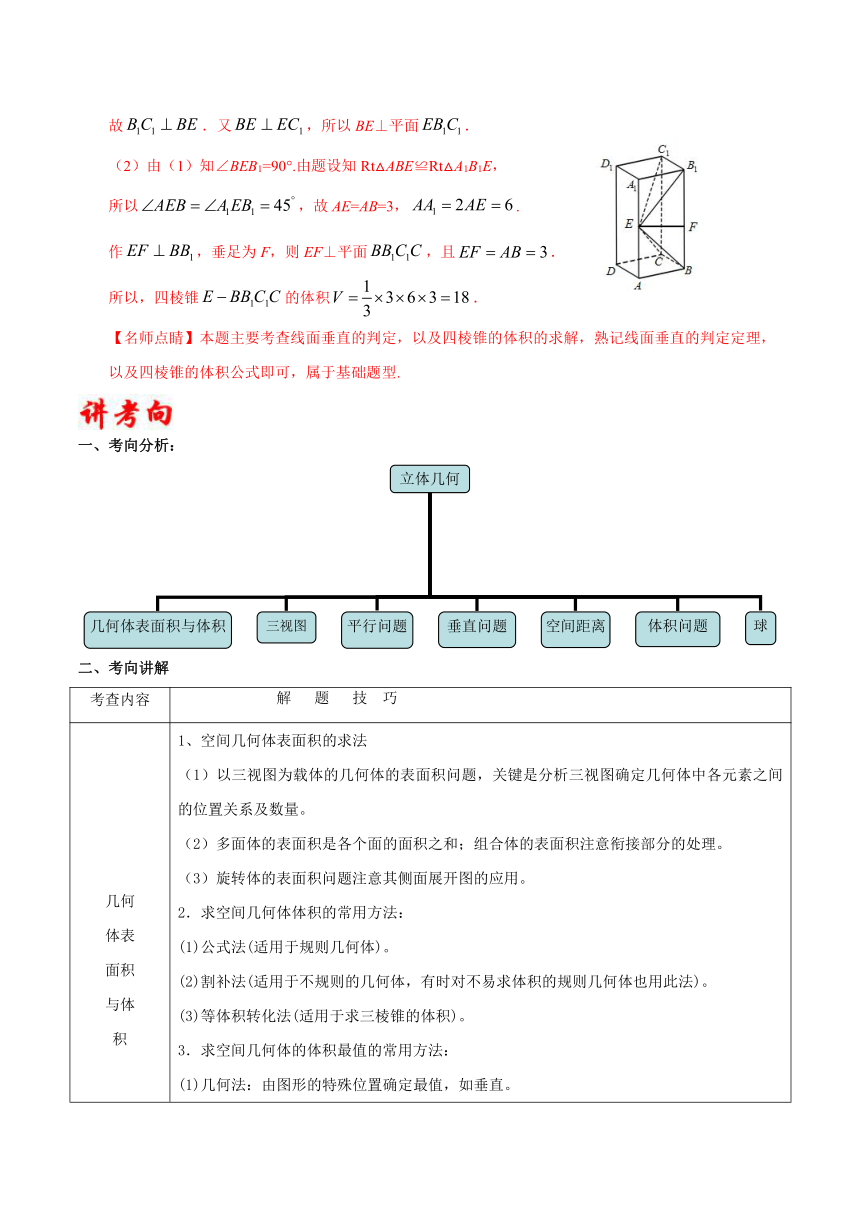
(2)由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,
所以,故AE=AB=3,.
作,垂足为F,则EF⊥平面,且.
所以,四棱锥的体积.
【名师点睛】本题主要考查线面垂直的判定,以及四棱锥的体积的求解,熟记线面垂直的判定定理,以及四棱锥的体积公式即可,属于基础题型.
一、考向分析:
二、考向讲解
考查内容
解
题
技
巧
几何体表面积与体积
1、空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量。(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理。(3)旋转体的表面积问题注意其侧面展开图的应用。2.求空间几何体体积的常用方法:(1)公式法(适用于规则几何体)。(2)割补法(适用于不规则的几何体,有时对不易求体积的规则几何体也用此法)。(3)等体积转化法(适用于求三棱锥的体积)。3.求空间几何体的体积最值的常用方法:(1)几何法:由图形的特殊位置确定最值,如垂直。(2)基本不等式法:根据条件建立两个变量的和或积为定值,利用基本不等式求体积的最值。(3)函数法:通过建立相关函数式,将所求的最值问题转化为函数的最值问题求解,此法应用最为广泛。
三视图
1、根据三视图还原几何体(1)对柱、锥、台、球的三视图要熟悉。(2)明确三视图的形成原理,并能结合空间想象将三视图还原为直观图。(3)根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据。提醒:对于简单组合体的三视图,首先要确定正视、侧视、俯视的方向,其次要注意组合体由哪些几何体组成,弄清它们的组成方式,特别应注意它们的交线的位置,区分好实线和虚线的不同。2、由三视图还原几何体的三个步骤:第一步,先画长(正)方体,在长(正)方体中画出俯视图;第二步,在三个视图中找直角;第三步,判断直角位置,并向上(或向下)做垂线,找到顶点,连线即可。
平行问题
1、证明线线平行的常用方法(1)利用公理4:找第三线,只需证明两线都与第三线平行即可.(2)利用三角形的中位线的性质.(3)构建平行四边形利用其对边平行.(4)利用面面平行的性质定理.2.判定线面平行的四种方法(1)利用线面平行的定义(无公共点)。(2)利用线面平行的判定定理(a?α,b?α,a∥b?a∥α)。(3)利用面面平行的性质定理(α∥β,a?α?a∥β)。(4)利用面面平行的性质(α∥β,a?α,a?β,a∥α?a∥β)。3.在应用线面平行的判定定理进行平行转化时,一定注意定理成立的条件,通常应严格按照定理成立的条件规范书写步骤,如:把线面平行转化为线线平行时,必须说清经过已知直线的平面和已知平面相交,这时才有直线与交线平行。4、证明面面平行的方法(1)面面平行的定义。(2)面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。(3)利用垂直于同一条直线的两个平面平行。(4)两个平面同时平行于第三个平面,那么这两个平面平行。(5)利用“线线平行”、“线面平行”、“面面平行”的相互转化。5.三种平行关系的转化:线线平行线面平行线线平行、线面平行、面面平行的相互转化是解决与平行有关的证明题的指导思想,解题中既要注意一般的转化规律,又要看清题目的具体条件,选择正确的转化方向。
垂直问题
1、证明直线和平面垂直的常用方法(1)利用判定定理.(2)利用平行线垂直于平面的传递性(a∥b,a⊥α?b⊥α).(3)利用面面平行的性质(a⊥α,α∥β?a⊥β).(4)利用面面垂直的性质.2、证明面面垂直的主要方法①利用判定定理.在审题时要注意直观判断哪条直线可能是垂线,充分利用等腰三角形底边上的中线垂直于底边,勾股定理的逆定理等.②用定义证明.只需判定两平面所成二面角为直二面角.③客观题中,也可应用:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于第三个平面.3、必记结论:(1)直线与平面垂直的定义常常逆用,即a⊥α,b?α?a⊥b.(2)若平行直线中一条垂直于平面,则另一条也垂直于该平面.(3)垂直于同一条直线的两个平面平行.(4)过一点有且只有一条直线与已知平面垂直.(5)过一点有且只有一个平面与已知直线垂直.4、垂直关系综合题的类型及解法(1)三种垂直的综合问题,一般通过作辅助线进行线线、线面、面面垂直间的转化。(2)垂直与平行结合问题,求解时应注意平行、垂直的性质及判定的综合应用。(3)垂直与体积结合问题,在求体积时,可根据线面垂直得到表示高的线段,进而求得体积。
体积问题
求几何体体积的常见类型及解题策略(1)以三视图为载体的几何体体积问题:将三视图还原为几何体,利用空间几何体的体积公式求解.(2)直观图中几何体的体积问题:①锥体、柱体的体积问题:根据题设条件求出所给几何体的底面积和高,直接套用公式求解;②球的体积问题:直接利用球的体积公式求解,在实际问题中要根据题意作出图形,构造直角三角形确定球的半径;③不规则几何体的体积问题:常用分割或补形的思想,若几何体的底不规则,也需采用同样的方法,将不规则的几何体或平面图形转化为规则的几何体或平面图形,易于求解.
探索性问题
解决探索性问题的方法(1)对命题条件的探索的三种途径途径一:先猜后证,即先观察与尝试给出条件再证明;途径二:先通过命题成立的必要条件探索出命题成立的条件,再证明充分性.途径三:将几何问题转化为代数问题,探索出命题成立的条件.(2)对命题结论的探索方法从条件出发,探索出要求的结论是什么,对于探索结论是否存在,求解时常假设结论存在,再寻找与条件相容或者矛盾的结论.
球体
1.正方体的外接球、内切球及与各条棱相切的球(1)外接球:球心是正方体中心;半径r=a(a为正方体的棱长)。(2)内切球:球心是正方体中心;半径r=(a为正方体的棱长)。(3)与各条棱都相切的球:球心是正方体中心;半径r=a(a为正方体的棱长)。2.正四面体的外接球与内切球(正四面体可以看作是正方体的一部分)(1)外接球:球心是正四面体的中心;半径r=a(a为正四面体的棱长)。(2)内切球:球心是正四面体的中心;半径r=a(a为正四面体的棱长)。
考查空间几何体的表面积与体积:
【例1】已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为(
)
A.
B.
C.
D.
【答案】B
【解析】截面面积为,高,底面半径,表面积.
【例2】在长方体中,,与平面所成的角为,则该长方体的体积为(
)
A.
B.
C.
D.
【答案】C
【解析】连接和,∵与平面所成角为,∴,∴,∴,∴,∴选C.
考查三视图:
【例1】某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为(
)
A.1
B.2
C.3
D.4
【答案】C
【解析】由三视图可得四棱锥,在四棱锥中,,,,,由勾股定理可知,,,,,则在四棱锥中,直角三角形有,,共三个,故选C.
【例2】某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,
从到的路径中,最短路径的长度为(
)
A.
B.
C.
D.2
【答案】B
【解析】三视图还原几何体为一圆柱,如图,
将侧面展开,最短路径为连线的距离,
所以,所以选B.
考查平行、垂直问题:
如图,在四棱锥中,底面为矩形,平面平面,,,,分别为,的中点.
(1)求证:;
(2)求证:平面平面;
(3)求证:平面.
【解析】(1),且为的中点,,
底面为矩形,,.
(2)底面为矩形,,平面平面,平面,.
又,平面,平面平面.
(3)如图,取中点,连接,.
,分别为和的中点,,且,
四边形为矩形,且为的中点,,,
,且,四边形为平行四边形,
,又平面,平面,平面.
【例2】如图,在四棱锥中,平面ABCD,底部ABCD为菱形,E为CD的中点.
(1)求证:BD⊥平面PAC;
(2)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(3)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
【答案】(1)见解析;(2)见解析;(3)存在,理由见解析.
【解析】(1)因为平面ABCD,所以.又因为底面ABCD为菱形,所以.
所以平面PAC.
(2)因为PA⊥平面ABCD,平面ABCD,所以PA⊥AE.
因为底面ABCD为菱形,∠ABC=60°,且E为CD的中点,所以AE⊥CD.
所以AB⊥AE.所以AE⊥平面PAB.所以平面PAB⊥平面PAE.
(3)棱PB上存在点F,使得CF∥平面PAE.取F为PB的中点,取G为PA的
中点,连结CF,FG,EG.则FG∥AB,且FG=AB.
因为底面ABCD为菱形,且E为CD的中点,所以CE∥AB,且CE=AB.
所以FG∥CE,且FG=CE.所以四边形CEGF为平行四边形.所以CF∥EG.
因为CF平面PAE,EG平面PAE,所以CF∥平面PAE.
【名师点睛】本题主要考查线面垂直的判定定理,面面垂直的判定定理,立体几何中的探索问题等知识,意在考查学生的转化能力和计算求解能力.
考查空间线线角、线面角:
【例】如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.
【答案】(1)证明见解析;(2);(3).
【解析】(1)由平面⊥平面,平面平面,,
可得平面,故.
(2)取棱的中点,连接,.又因为为棱的中点,故.
所以(或其补角)为异面直线与所成的角.
在中,,故,因为平面,
故.在中,,故.
在等腰三角形中,,可得.
所以,异面直线与所成角的余弦值为.
(3)连接,因为为等边三角形,为边的中点,故,.又因为平面⊥平面,而平面,故平面.
所以,为直线与平面所成的角.
在中,.在中,.
所以,直线与平面所成角的正弦值为.
1.如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求出该几何体的体积.
【解析】(Ⅰ)∵M为DB的中点,取BC中点G,连接EM、MG、AG,
则MG∥DC,且
∴MG∥AE且MG
=
AE
故四边形AGME为平行四边形,∴EM∥AG
又AG?平面ABC,EM平面ABC,∴EM∥平面ABC.
(Ⅱ)由已知,AE
=
2,DC
=
4,AB⊥AC,且AB
=
AC
=
2∵EA⊥平面ABC,∴EA⊥AB
又AB⊥AC,∴AB⊥平面ACDE∴AB是四棱锥B-ACDE的高,
梯形ACDE的面积
∴,即所求几何体的体积为4.
2.已知四棱锥中,底面,,,,.
(1)当变化时,点到平面的距离是否为定值?若是,请求出该定值;若不是,请说明理由;
(2)若,求直线与平面所成角的正弦值.
【解析】(1)由,,知,则,
由平面,平面,得,
由,,平面,
得平面,
则点到平面的距离为一个定值,且.
(2)设直线与平面所成的角为,
由,可知,
又平面,平面,
故,
又,
则平面,
则点到平面的距离为,
由知点与点到平面的距离相等,
则点到平面的距离为,
由知,
故.
考查球体:
【例1】在三棱锥中,平面平面,是边长为6的等边三角形,是以为斜边的等腰直角三角形,则该三棱锥外接球的表面积为_______.
【答案】
【解析】如图,在等边三角形中,取的中点,设等边三角形的中心为,连接PF,CF,OP.由,得,
是以为斜边的等腰角三角形,,
又平面平面,平面,
,,则为棱锥的
外接球球心,外接球半径,该三棱锥外接球的表面积为,
【名师点睛】本题主要考查四面体外接球表面积,考查空间想象能力,是中档题.
要求外接球的表面积和体积,关键是求出球的半径.求外接球半径的常见方法有:①若三条棱两两垂直,则用(为三条棱的长);②若面(),则(为外接圆半径);③可以转化为长方体的外接球;④特殊几何体可以直接找出球心和半径.
与球相关的切、接问题是高考命题的热点,也是考生的难点、易失分点.命题角度多变.归纳起来常见的命题角度有:
四面体的外接球问题
【例】正三棱锥的高和底面边长都等于6,则其外接球的表面积为( )
A.64π
B.32π
C.16π
D.8π
【答案】A
【解析】如图,作PM⊥平面ABC于点M,则球心O在PM上,PM=6,连接AM,AO,则OP=OA=R(R为外接球半径),在Rt△OAM中,OM=6-R,OA=R,又AB=6,且△ABC为等边三角形,故AM==2,则R2-(6-R)2=(2)2,则R=4,所以球的表面积S=4πR2=64π.
四棱锥的外接球问题
【例】已知四棱锥P?ABCD的顶点都在球O的球面上,底面ABCD是矩形,平面PAD⊥底面ABCD,△PAD为正三角形,AB=2AD=4,则球O的表面积为( )
A.π
B.32π
C.64π
D.π
【答案】D
【解析】依题意,AB⊥平面PAD且△PAD是正三角形,过P点作AB的平行线,交球面于点E,连接BE,CE,则可得到正三棱柱APD?BEC.因为△PAD是正三角形,且AD=2,所以△PAD的外接圆半径是,球O的半径R==,球O的表面积S=4πR2=,故选D.
三棱柱的外接球问题
【例】已知三棱柱ABC?A1B1C1的底面是边长为的正三角形,侧棱垂直于底面,且该三棱柱的外接球的表面积为12π,则该三棱柱的体积为________.
【答案】3
【解析】设球半径为R,上,下底面中心设为M,N,由题意,外接球心为MN的中点,设为O,则OA=R,由4πR2=12π,得R=OA=,又易得AM=,由勾股定理可知,OM=1,所以MN=2,即棱柱的高h=2,所以该三棱柱的体积为×()2×2=3.
四面体的内切球问题
【例】若一个正四面体的表面积为S1,其内切球的表面积为S2,则=________.
【答案】
【解析】设正四面体棱长为a,则正四面体表面积为S1=4··a2=a2,其内切球半径为正四面体高的,即r=·a=a,因此内切球表面积为S2=4πr2=,则==.
求解与球有关的切、接问题的关键点:
解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.
立体几何
几何体表面积与体积
体积问题
空间距离
垂直问题
平行问题
球
三视图
2
4
A
B
C
D
E
M
直观图
侧视图
俯视图
立体几何
1.【2019年高考全国Ⅱ卷文数】设α,β为两个平面,则α∥β的充要条件是
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面
【答案】B
【解析】由面面平行的判定定理知:内两条相交直线都与平行是的充分条件,由面面平行性质定理知,若,则内任意一条直线都与平行,所以内两条相交直线都与平行是的必要条件,故选B.
【名师点睛】本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用面面平行的判定定理与性质定理即可作出判断.面面平行的判定问题要紧扣面面平行判定定理,最容易犯的错误为定理记不住,凭主观臆断,如:“若,则”此类的错误.
2.【2019年高考全国Ⅲ卷文数】如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则()
A.BM=EN,且直线BM,EN是相交直线
B.BM≠EN,且直线BM,EN是相交直线
C.BM=EN,且直线BM,EN是异面直线
D.BM≠EN,且直线BM,EN是异面直线
【答案】B
【解析】如图所示,作于,连接,BD,易得直线BM,EN
是三角形EBD的中线,是相交直线.过作于,连接,平面平面,平面,平面,平面,与均为直角三角形.设正方形边长为2,易知,,,故选B.
【名师点睛】本题考查空间想象能力和计算能力,解答本题的关键是构造直角三角形.解答本题时,先利用垂直关系,再结合勾股定理进而解决问题.
3.【2019年高考江苏卷】如图,长方体的体积是120,E为的中点,则三棱锥E?BCD的体积是
▲
.
【答案】10
【解析】因为长方体的体积为120,所以,因为为的中点,所以,由长方体的性质知底面,所以是三棱锥的底面上的高,所以三棱锥的体积.
【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中,往往需要注意理清整体和局部的关系,灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.
4.【2019年高考全国Ⅱ卷文数】如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,AB=3,求四棱锥的体积.
【答案】(1)见详解;(2)18.
【解析】(1)由已知得B1C1⊥平面ABB1A1,BE平面ABB1A1,
故.又,所以BE⊥平面.
(2)由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,
所以,故AE=AB=3,.
作,垂足为F,则EF⊥平面,且.
所以,四棱锥的体积.
【名师点睛】本题主要考查线面垂直的判定,以及四棱锥的体积的求解,熟记线面垂直的判定定理,以及四棱锥的体积公式即可,属于基础题型.
一、考向分析:
二、考向讲解
考查内容
解
题
技
巧
几何体表面积与体积
1、空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量。(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理。(3)旋转体的表面积问题注意其侧面展开图的应用。2.求空间几何体体积的常用方法:(1)公式法(适用于规则几何体)。(2)割补法(适用于不规则的几何体,有时对不易求体积的规则几何体也用此法)。(3)等体积转化法(适用于求三棱锥的体积)。3.求空间几何体的体积最值的常用方法:(1)几何法:由图形的特殊位置确定最值,如垂直。(2)基本不等式法:根据条件建立两个变量的和或积为定值,利用基本不等式求体积的最值。(3)函数法:通过建立相关函数式,将所求的最值问题转化为函数的最值问题求解,此法应用最为广泛。
三视图
1、根据三视图还原几何体(1)对柱、锥、台、球的三视图要熟悉。(2)明确三视图的形成原理,并能结合空间想象将三视图还原为直观图。(3)根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据。提醒:对于简单组合体的三视图,首先要确定正视、侧视、俯视的方向,其次要注意组合体由哪些几何体组成,弄清它们的组成方式,特别应注意它们的交线的位置,区分好实线和虚线的不同。2、由三视图还原几何体的三个步骤:第一步,先画长(正)方体,在长(正)方体中画出俯视图;第二步,在三个视图中找直角;第三步,判断直角位置,并向上(或向下)做垂线,找到顶点,连线即可。
平行问题
1、证明线线平行的常用方法(1)利用公理4:找第三线,只需证明两线都与第三线平行即可.(2)利用三角形的中位线的性质.(3)构建平行四边形利用其对边平行.(4)利用面面平行的性质定理.2.判定线面平行的四种方法(1)利用线面平行的定义(无公共点)。(2)利用线面平行的判定定理(a?α,b?α,a∥b?a∥α)。(3)利用面面平行的性质定理(α∥β,a?α?a∥β)。(4)利用面面平行的性质(α∥β,a?α,a?β,a∥α?a∥β)。3.在应用线面平行的判定定理进行平行转化时,一定注意定理成立的条件,通常应严格按照定理成立的条件规范书写步骤,如:把线面平行转化为线线平行时,必须说清经过已知直线的平面和已知平面相交,这时才有直线与交线平行。4、证明面面平行的方法(1)面面平行的定义。(2)面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。(3)利用垂直于同一条直线的两个平面平行。(4)两个平面同时平行于第三个平面,那么这两个平面平行。(5)利用“线线平行”、“线面平行”、“面面平行”的相互转化。5.三种平行关系的转化:线线平行线面平行线线平行、线面平行、面面平行的相互转化是解决与平行有关的证明题的指导思想,解题中既要注意一般的转化规律,又要看清题目的具体条件,选择正确的转化方向。
垂直问题
1、证明直线和平面垂直的常用方法(1)利用判定定理.(2)利用平行线垂直于平面的传递性(a∥b,a⊥α?b⊥α).(3)利用面面平行的性质(a⊥α,α∥β?a⊥β).(4)利用面面垂直的性质.2、证明面面垂直的主要方法①利用判定定理.在审题时要注意直观判断哪条直线可能是垂线,充分利用等腰三角形底边上的中线垂直于底边,勾股定理的逆定理等.②用定义证明.只需判定两平面所成二面角为直二面角.③客观题中,也可应用:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于第三个平面.3、必记结论:(1)直线与平面垂直的定义常常逆用,即a⊥α,b?α?a⊥b.(2)若平行直线中一条垂直于平面,则另一条也垂直于该平面.(3)垂直于同一条直线的两个平面平行.(4)过一点有且只有一条直线与已知平面垂直.(5)过一点有且只有一个平面与已知直线垂直.4、垂直关系综合题的类型及解法(1)三种垂直的综合问题,一般通过作辅助线进行线线、线面、面面垂直间的转化。(2)垂直与平行结合问题,求解时应注意平行、垂直的性质及判定的综合应用。(3)垂直与体积结合问题,在求体积时,可根据线面垂直得到表示高的线段,进而求得体积。
体积问题
求几何体体积的常见类型及解题策略(1)以三视图为载体的几何体体积问题:将三视图还原为几何体,利用空间几何体的体积公式求解.(2)直观图中几何体的体积问题:①锥体、柱体的体积问题:根据题设条件求出所给几何体的底面积和高,直接套用公式求解;②球的体积问题:直接利用球的体积公式求解,在实际问题中要根据题意作出图形,构造直角三角形确定球的半径;③不规则几何体的体积问题:常用分割或补形的思想,若几何体的底不规则,也需采用同样的方法,将不规则的几何体或平面图形转化为规则的几何体或平面图形,易于求解.
探索性问题
解决探索性问题的方法(1)对命题条件的探索的三种途径途径一:先猜后证,即先观察与尝试给出条件再证明;途径二:先通过命题成立的必要条件探索出命题成立的条件,再证明充分性.途径三:将几何问题转化为代数问题,探索出命题成立的条件.(2)对命题结论的探索方法从条件出发,探索出要求的结论是什么,对于探索结论是否存在,求解时常假设结论存在,再寻找与条件相容或者矛盾的结论.
球体
1.正方体的外接球、内切球及与各条棱相切的球(1)外接球:球心是正方体中心;半径r=a(a为正方体的棱长)。(2)内切球:球心是正方体中心;半径r=(a为正方体的棱长)。(3)与各条棱都相切的球:球心是正方体中心;半径r=a(a为正方体的棱长)。2.正四面体的外接球与内切球(正四面体可以看作是正方体的一部分)(1)外接球:球心是正四面体的中心;半径r=a(a为正四面体的棱长)。(2)内切球:球心是正四面体的中心;半径r=a(a为正四面体的棱长)。
考查空间几何体的表面积与体积:
【例1】已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为(
)
A.
B.
C.
D.
【答案】B
【解析】截面面积为,高,底面半径,表面积.
【例2】在长方体中,,与平面所成的角为,则该长方体的体积为(
)
A.
B.
C.
D.
【答案】C
【解析】连接和,∵与平面所成角为,∴,∴,∴,∴,∴选C.
考查三视图:
【例1】某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为(
)
A.1
B.2
C.3
D.4
【答案】C
【解析】由三视图可得四棱锥,在四棱锥中,,,,,由勾股定理可知,,,,,则在四棱锥中,直角三角形有,,共三个,故选C.
【例2】某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,
从到的路径中,最短路径的长度为(
)
A.
B.
C.
D.2
【答案】B
【解析】三视图还原几何体为一圆柱,如图,
将侧面展开,最短路径为连线的距离,
所以,所以选B.
考查平行、垂直问题:
如图,在四棱锥中,底面为矩形,平面平面,,,,分别为,的中点.
(1)求证:;
(2)求证:平面平面;
(3)求证:平面.
【解析】(1),且为的中点,,
底面为矩形,,.
(2)底面为矩形,,平面平面,平面,.
又,平面,平面平面.
(3)如图,取中点,连接,.
,分别为和的中点,,且,
四边形为矩形,且为的中点,,,
,且,四边形为平行四边形,
,又平面,平面,平面.
【例2】如图,在四棱锥中,平面ABCD,底部ABCD为菱形,E为CD的中点.
(1)求证:BD⊥平面PAC;
(2)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(3)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
【答案】(1)见解析;(2)见解析;(3)存在,理由见解析.
【解析】(1)因为平面ABCD,所以.又因为底面ABCD为菱形,所以.
所以平面PAC.
(2)因为PA⊥平面ABCD,平面ABCD,所以PA⊥AE.
因为底面ABCD为菱形,∠ABC=60°,且E为CD的中点,所以AE⊥CD.
所以AB⊥AE.所以AE⊥平面PAB.所以平面PAB⊥平面PAE.
(3)棱PB上存在点F,使得CF∥平面PAE.取F为PB的中点,取G为PA的
中点,连结CF,FG,EG.则FG∥AB,且FG=AB.
因为底面ABCD为菱形,且E为CD的中点,所以CE∥AB,且CE=AB.
所以FG∥CE,且FG=CE.所以四边形CEGF为平行四边形.所以CF∥EG.
因为CF平面PAE,EG平面PAE,所以CF∥平面PAE.
【名师点睛】本题主要考查线面垂直的判定定理,面面垂直的判定定理,立体几何中的探索问题等知识,意在考查学生的转化能力和计算求解能力.
考查空间线线角、线面角:
【例】如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.
【答案】(1)证明见解析;(2);(3).
【解析】(1)由平面⊥平面,平面平面,,
可得平面,故.
(2)取棱的中点,连接,.又因为为棱的中点,故.
所以(或其补角)为异面直线与所成的角.
在中,,故,因为平面,
故.在中,,故.
在等腰三角形中,,可得.
所以,异面直线与所成角的余弦值为.
(3)连接,因为为等边三角形,为边的中点,故,.又因为平面⊥平面,而平面,故平面.
所以,为直线与平面所成的角.
在中,.在中,.
所以,直线与平面所成角的正弦值为.
1.如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求出该几何体的体积.
【解析】(Ⅰ)∵M为DB的中点,取BC中点G,连接EM、MG、AG,
则MG∥DC,且
∴MG∥AE且MG
=
AE
故四边形AGME为平行四边形,∴EM∥AG
又AG?平面ABC,EM平面ABC,∴EM∥平面ABC.
(Ⅱ)由已知,AE
=
2,DC
=
4,AB⊥AC,且AB
=
AC
=
2∵EA⊥平面ABC,∴EA⊥AB
又AB⊥AC,∴AB⊥平面ACDE∴AB是四棱锥B-ACDE的高,
梯形ACDE的面积
∴,即所求几何体的体积为4.
2.已知四棱锥中,底面,,,,.
(1)当变化时,点到平面的距离是否为定值?若是,请求出该定值;若不是,请说明理由;
(2)若,求直线与平面所成角的正弦值.
【解析】(1)由,,知,则,
由平面,平面,得,
由,,平面,
得平面,
则点到平面的距离为一个定值,且.
(2)设直线与平面所成的角为,
由,可知,
又平面,平面,
故,
又,
则平面,
则点到平面的距离为,
由知点与点到平面的距离相等,
则点到平面的距离为,
由知,
故.
考查球体:
【例1】在三棱锥中,平面平面,是边长为6的等边三角形,是以为斜边的等腰直角三角形,则该三棱锥外接球的表面积为_______.
【答案】
【解析】如图,在等边三角形中,取的中点,设等边三角形的中心为,连接PF,CF,OP.由,得,
是以为斜边的等腰角三角形,,
又平面平面,平面,
,,则为棱锥的
外接球球心,外接球半径,该三棱锥外接球的表面积为,
【名师点睛】本题主要考查四面体外接球表面积,考查空间想象能力,是中档题.
要求外接球的表面积和体积,关键是求出球的半径.求外接球半径的常见方法有:①若三条棱两两垂直,则用(为三条棱的长);②若面(),则(为外接圆半径);③可以转化为长方体的外接球;④特殊几何体可以直接找出球心和半径.
与球相关的切、接问题是高考命题的热点,也是考生的难点、易失分点.命题角度多变.归纳起来常见的命题角度有:
四面体的外接球问题
【例】正三棱锥的高和底面边长都等于6,则其外接球的表面积为( )
A.64π
B.32π
C.16π
D.8π
【答案】A
【解析】如图,作PM⊥平面ABC于点M,则球心O在PM上,PM=6,连接AM,AO,则OP=OA=R(R为外接球半径),在Rt△OAM中,OM=6-R,OA=R,又AB=6,且△ABC为等边三角形,故AM==2,则R2-(6-R)2=(2)2,则R=4,所以球的表面积S=4πR2=64π.
四棱锥的外接球问题
【例】已知四棱锥P?ABCD的顶点都在球O的球面上,底面ABCD是矩形,平面PAD⊥底面ABCD,△PAD为正三角形,AB=2AD=4,则球O的表面积为( )
A.π
B.32π
C.64π
D.π
【答案】D
【解析】依题意,AB⊥平面PAD且△PAD是正三角形,过P点作AB的平行线,交球面于点E,连接BE,CE,则可得到正三棱柱APD?BEC.因为△PAD是正三角形,且AD=2,所以△PAD的外接圆半径是,球O的半径R==,球O的表面积S=4πR2=,故选D.
三棱柱的外接球问题
【例】已知三棱柱ABC?A1B1C1的底面是边长为的正三角形,侧棱垂直于底面,且该三棱柱的外接球的表面积为12π,则该三棱柱的体积为________.
【答案】3
【解析】设球半径为R,上,下底面中心设为M,N,由题意,外接球心为MN的中点,设为O,则OA=R,由4πR2=12π,得R=OA=,又易得AM=,由勾股定理可知,OM=1,所以MN=2,即棱柱的高h=2,所以该三棱柱的体积为×()2×2=3.
四面体的内切球问题
【例】若一个正四面体的表面积为S1,其内切球的表面积为S2,则=________.
【答案】
【解析】设正四面体棱长为a,则正四面体表面积为S1=4··a2=a2,其内切球半径为正四面体高的,即r=·a=a,因此内切球表面积为S2=4πr2=,则==.
求解与球有关的切、接问题的关键点:
解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.
立体几何
几何体表面积与体积
体积问题
空间距离
垂直问题
平行问题
球
三视图
2
4
A
B
C
D
E
M
直观图
侧视图
俯视图
同课章节目录
