六年级下册数学课件-7.1 比和比例整理与复习 苏教版 (共20张PPT)
文档属性
| 名称 | 六年级下册数学课件-7.1 比和比例整理与复习 苏教版 (共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 404.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-15 21:25:39 | ||
图片预览








文档简介
正比例、反比例整理和复习
苏教版小学数学六年级下册
知识回顾:
在上节课的复习中,已经对比、比例的知识进行了巩固,回想一下:
什么是比的意义?
什么是 比的基本性质?
什么是比例?
什么是比例的基本性质?
教学目标:
1、通过回顾与交流,鼓励学生自己独立整理知识,形 成系统。
2、通过具体问题的认识,使同学们能够迅速的判断两种相关联的量成不成比例,成什么比例。
3、通过复习与整理加深对正、反比例意义的理解,并运用正、反比例的知识解决实际问题。
4、通过练习进一步提高同学们综合运用有关知识解决实际问题的能力,培养同学们自主探究、合作交流的学习能力。
小组讨论:
1、什么叫做正比例?
2、什么叫做反比例?
3、正比例和反比例的区别?
4、如何判断是否成正、反比例关系?
5、正、反比例图像?(重点:正比例图像)
小组展示:
1、什么叫做正比例?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,那么这两种量成正比例关系。
=
y
x
_
K(一定)
2、什么叫做反比例?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,那么这两种量成反比例关系。
Xy=k(一定)
3、正比例和反比例的区别
{5940675A-B579-460E-94D1-54222C63F5DA}比例
相同点
不同点
正比例
反比例
两种相关联的量,一种量变化,另一种量也随着变化。
两种量的变化,同时扩大或同时缩小
一种量扩大,另一种量反而缩小。
比值一定
积一定
4、如何判断是否成正比例、反比例关系。
方法:“一找、二想、三判断”
一找:哪两种量;
二想:两种相关联量的变化情况,写出关系式。
三判断:联系关系式,看商一定还是积一定,判断成什么比例。
5、举例
(1)被除数÷除数=商(一定)
(2)除数×商=被除数(一定)
(3)因数×因数=积(一定)
(4)积÷因数=因数(一定)
(正比例关系)
(反比例关系)
(反比例关系)
(正比例关系)
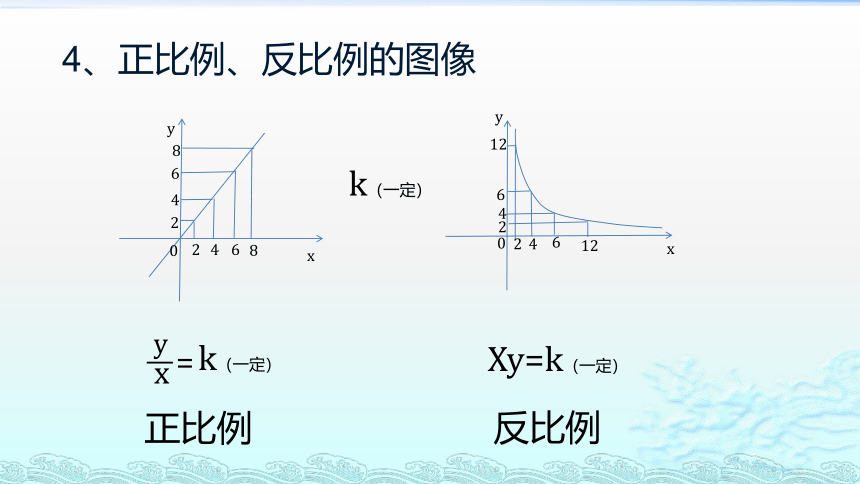
4、正比例、反比例的图像
正比例
反比例
0
2
4
6
8
2
4
6
8
y
x
0
2
4
2
4
6
12
12
6
y
x
k(一定)
y
x
—
=
k(一定)
Xy=k(一定)
试一试:
火眼金睛(判断下面各题的两个量是否成比例?如果成比例,成什么比例关系?)
(1)做一个零件的时间一定,做的零件总个数和总时间。( )
(2)减数一定,被减数与差。( )
不成比例关系
正比例关系
做的零件总个数
总时间
=
做一个零件的时间(一定)
被减数—差=减数(一定)
(3)小明拿一些钱购买铅笔,单价和购买的数量。( )
(4)圆的周长与直径。( )
单价×购买数量=总价(一定)
反比例关系
C
d
—
=
∏(一定)
正比例关系
练习与实践(1)
{5940675A-B579-460E-94D1-54222C63F5DA}比的前项
0.3
2
5
比的后项
6
40
100
{5940675A-B579-460E-94D1-54222C63F5DA}小麦的质量∕kg
5
10
15
磨面粉的质量∕kg
3.5
7
10.5
2
40
—
=
0.05
5
100
—
=
0.05
0.3
6
—
=
0.05
3.5
5
—
=
0.7
10.5
15
—
=
0.7
比的前项
比的后项
=
比值(一定)
磨面粉的质量
小麦的质量
=
出粉率(一定)
比的前项和比的后项成正比例
小麦的质量和磨面粉的质量成正比例
{5940675A-B579-460E-94D1-54222C63F5DA}三角形的底∕cm
8
12
16
三角形的高∕cm
6
4
3
{5940675A-B579-460E-94D1-54222C63F5DA}圆的半径∕cm
1
2
3
圆的面积∕kg
3.14
12.56
28.26
8 ×6=48 12 ×4=48 16 ×3=48
三角形的底×三角形的高=
三角形的底和三角形的高成反比例
圆的半径和圆的面积不成比例
积(一定)
8.判断各题的两种量是否成比例,成比例的是成正比例还是反
比例?
(1)步测一段距离,每步的平均长度和走的步数。
答:每步的平均长度和走的步数成反比例。
(2)一台压路机滚筒滚动的转数和压路的面积。
答:一台压路机滚筒滚动的转数和压路的面积成正比例。
(3)一台收割机每小时收割麦子的面积一定,麦地面积和收割时间。
答:麦地面积和收割时间成正比例。
每步的平均长度×走的步数=总米数(一定)
压路的总面积
滚动的转数
滚筒滚动一圈压路的面积(一定)
=
麦地总面积
收割时间
每小时收割麦子的面积(一定)
=
练习与实践(2)
(4)图书室的藏书数量一定,每天借出和还回的书的本数。
答:每天借出和还回的书的本数不成比例。
(5)已知 x y = 10, x 和 y。
答: x和y成反比例。
x× y = 10(一定)
练习与实践(2)
巩固提升:
X和Y是两种相关联的量:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}X
2
3
Y
4
(1)当X和Y成正比例时,Y的值为( )
(2)当X和Y成反比例时,Y的值为( )
答:这辆汽车在高速公路上行驶的路程和耗油量成正比例,
因为每升油行驶的路程是一定的。
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
拓展练习
答:行驶75千米耗油6升。
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
(2)根据图像判断?行驶75
千米耗油多少升?
75
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
(3)汽车在市区行驶,每行50千米耗油 6升, 照这样的耗油
量,在上图中描出行驶50千米、100 千米… …路程和耗
油量对应的点,再按顺序连接起来。
(2)根据图像判断?行驶75
千米耗油多少升?
课末总结:
本节课,你复习巩固了什么内容?
你能不能联系上节课内容,画一个思维导图?
(比、比例)
谢谢!
苏教版小学数学六年级下册
知识回顾:
在上节课的复习中,已经对比、比例的知识进行了巩固,回想一下:
什么是比的意义?
什么是 比的基本性质?
什么是比例?
什么是比例的基本性质?
教学目标:
1、通过回顾与交流,鼓励学生自己独立整理知识,形 成系统。
2、通过具体问题的认识,使同学们能够迅速的判断两种相关联的量成不成比例,成什么比例。
3、通过复习与整理加深对正、反比例意义的理解,并运用正、反比例的知识解决实际问题。
4、通过练习进一步提高同学们综合运用有关知识解决实际问题的能力,培养同学们自主探究、合作交流的学习能力。
小组讨论:
1、什么叫做正比例?
2、什么叫做反比例?
3、正比例和反比例的区别?
4、如何判断是否成正、反比例关系?
5、正、反比例图像?(重点:正比例图像)
小组展示:
1、什么叫做正比例?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,那么这两种量成正比例关系。
=
y
x
_
K(一定)
2、什么叫做反比例?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,那么这两种量成反比例关系。
Xy=k(一定)
3、正比例和反比例的区别
{5940675A-B579-460E-94D1-54222C63F5DA}比例
相同点
不同点
正比例
反比例
两种相关联的量,一种量变化,另一种量也随着变化。
两种量的变化,同时扩大或同时缩小
一种量扩大,另一种量反而缩小。
比值一定
积一定
4、如何判断是否成正比例、反比例关系。
方法:“一找、二想、三判断”
一找:哪两种量;
二想:两种相关联量的变化情况,写出关系式。
三判断:联系关系式,看商一定还是积一定,判断成什么比例。
5、举例
(1)被除数÷除数=商(一定)
(2)除数×商=被除数(一定)
(3)因数×因数=积(一定)
(4)积÷因数=因数(一定)
(正比例关系)
(反比例关系)
(反比例关系)
(正比例关系)
4、正比例、反比例的图像
正比例
反比例
0
2
4
6
8
2
4
6
8
y
x
0
2
4
2
4
6
12
12
6
y
x
k(一定)
y
x
—
=
k(一定)
Xy=k(一定)
试一试:
火眼金睛(判断下面各题的两个量是否成比例?如果成比例,成什么比例关系?)
(1)做一个零件的时间一定,做的零件总个数和总时间。( )
(2)减数一定,被减数与差。( )
不成比例关系
正比例关系
做的零件总个数
总时间
=
做一个零件的时间(一定)
被减数—差=减数(一定)
(3)小明拿一些钱购买铅笔,单价和购买的数量。( )
(4)圆的周长与直径。( )
单价×购买数量=总价(一定)
反比例关系
C
d
—
=
∏(一定)
正比例关系
练习与实践(1)
{5940675A-B579-460E-94D1-54222C63F5DA}比的前项
0.3
2
5
比的后项
6
40
100
{5940675A-B579-460E-94D1-54222C63F5DA}小麦的质量∕kg
5
10
15
磨面粉的质量∕kg
3.5
7
10.5
2
40
—
=
0.05
5
100
—
=
0.05
0.3
6
—
=
0.05
3.5
5
—
=
0.7
10.5
15
—
=
0.7
比的前项
比的后项
=
比值(一定)
磨面粉的质量
小麦的质量
=
出粉率(一定)
比的前项和比的后项成正比例
小麦的质量和磨面粉的质量成正比例
{5940675A-B579-460E-94D1-54222C63F5DA}三角形的底∕cm
8
12
16
三角形的高∕cm
6
4
3
{5940675A-B579-460E-94D1-54222C63F5DA}圆的半径∕cm
1
2
3
圆的面积∕kg
3.14
12.56
28.26
8 ×6=48 12 ×4=48 16 ×3=48
三角形的底×三角形的高=
三角形的底和三角形的高成反比例
圆的半径和圆的面积不成比例
积(一定)
8.判断各题的两种量是否成比例,成比例的是成正比例还是反
比例?
(1)步测一段距离,每步的平均长度和走的步数。
答:每步的平均长度和走的步数成反比例。
(2)一台压路机滚筒滚动的转数和压路的面积。
答:一台压路机滚筒滚动的转数和压路的面积成正比例。
(3)一台收割机每小时收割麦子的面积一定,麦地面积和收割时间。
答:麦地面积和收割时间成正比例。
每步的平均长度×走的步数=总米数(一定)
压路的总面积
滚动的转数
滚筒滚动一圈压路的面积(一定)
=
麦地总面积
收割时间
每小时收割麦子的面积(一定)
=
练习与实践(2)
(4)图书室的藏书数量一定,每天借出和还回的书的本数。
答:每天借出和还回的书的本数不成比例。
(5)已知 x y = 10, x 和 y。
答: x和y成反比例。
x× y = 10(一定)
练习与实践(2)
巩固提升:
X和Y是两种相关联的量:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}X
2
3
Y
4
(1)当X和Y成正比例时,Y的值为( )
(2)当X和Y成反比例时,Y的值为( )
答:这辆汽车在高速公路上行驶的路程和耗油量成正比例,
因为每升油行驶的路程是一定的。
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
拓展练习
答:行驶75千米耗油6升。
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
(2)根据图像判断?行驶75
千米耗油多少升?
75
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
(3)汽车在市区行驶,每行50千米耗油 6升, 照这样的耗油
量,在上图中描出行驶50千米、100 千米… …路程和耗
油量对应的点,再按顺序连接起来。
(2)根据图像判断?行驶75
千米耗油多少升?
课末总结:
本节课,你复习巩固了什么内容?
你能不能联系上节课内容,画一个思维导图?
(比、比例)
谢谢!
