人教版九年级数学上册23.1旋转的概念及性质同步练习(第1课时 Word版 含答案)
文档属性
| 名称 | 人教版九年级数学上册23.1旋转的概念及性质同步练习(第1课时 Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 188.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-16 00:00:00 | ||
图片预览


文档简介
23.1 第1课时 旋转的概念及性质
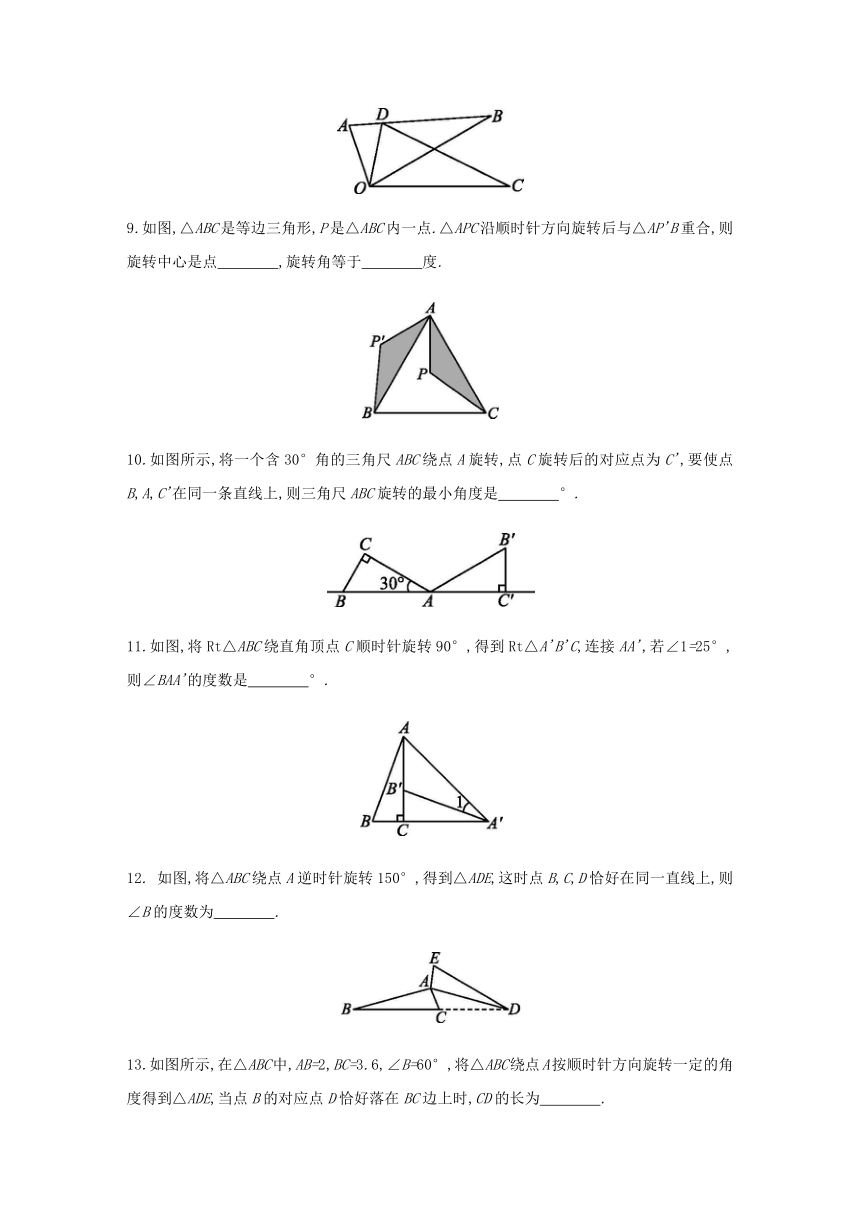
1.下列现象中是旋转的是( )
A.推拉抽屉
B.火车车厢的直线运动
C.电梯的上下移动
D.汽车方向盘的转动
2.将图按顺时针方向旋转90°后得到的图形是图中的( )
3
如图,E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为
( )
A.5
B.
C.7
D.
4
如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是
( )
A.AC=AD
B.AB⊥EB
C.BC=DE
D.∠A=∠EBC
5如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则点P'的坐标为
( )
A.(3,2)
B.(3,-1)
C.(2,-3)
D.(3,-2)
6
如图,△A'B'C'是由△ABC经过平移得到的,△A'B'C'还可以看作是由△ABC经过怎样的图形变化得到的?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
A.①④
B.②③
C.②④
D.③④
7.如图所示,△AOB绕着点O顺时针旋转至△A'OB'的位置,此时:
(1)点B的对应点是 ;?
(2)旋转中心是 ,旋转角为 ;?
(3)∠A的对应角是 ,线段OB的对应线段是 .?
8.如图,△ODC是由△OAB绕点O顺时针旋转30°得到的图形,点D在线段AB上.图中相等的线段有 ;图中等于30°的角有 ;图中的全等三角形是 ;图中的等腰三角形是 .?
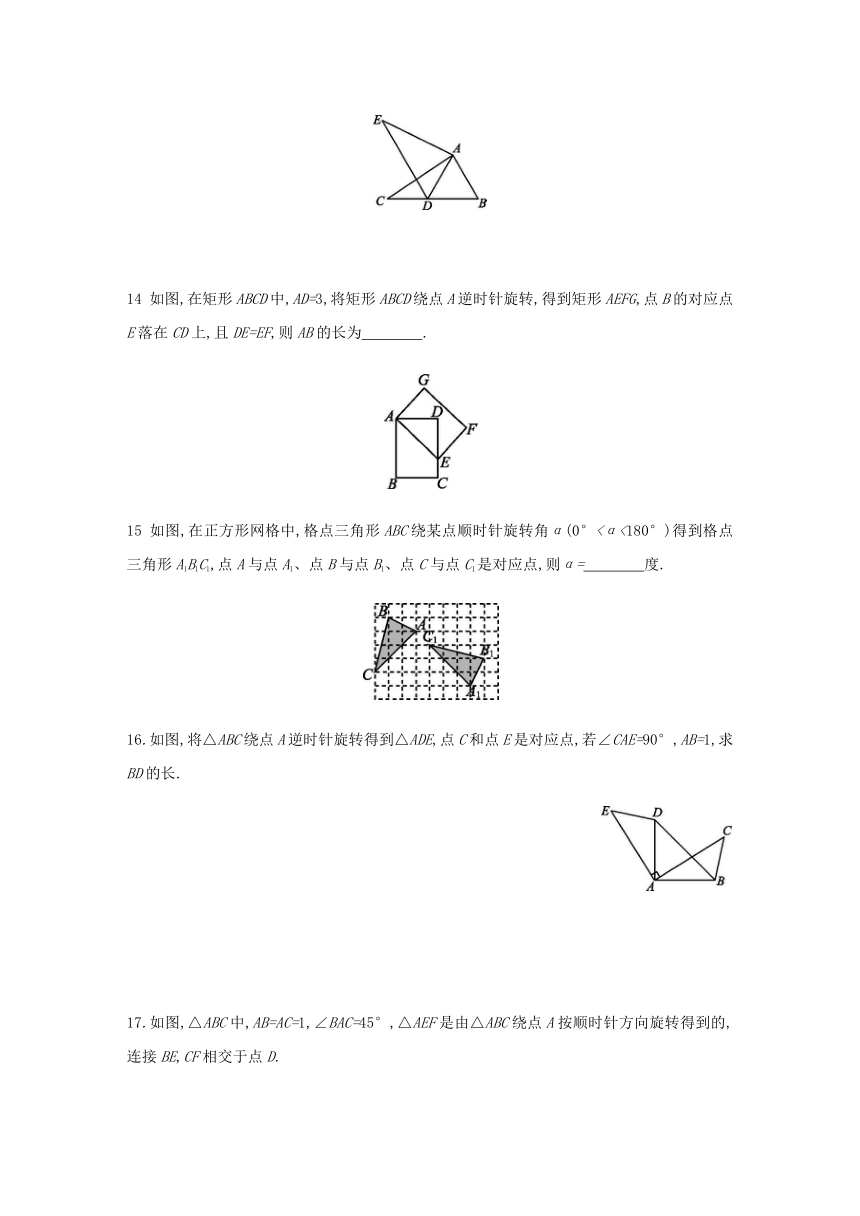
9.如图,△ABC是等边三角形,P是△ABC内一点.△APC沿顺时针方向旋转后与△AP'B重合,则旋转中心是点 ,旋转角等于 度.?
10.如图所示,将一个含30°角的三角尺ABC绕点A旋转,点C旋转后的对应点为C',要使点B,A,C'在同一条直线上,则三角尺ABC旋转的最小角度是 °.?
11.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到Rt△A'B'C,连接AA',若∠1=25°,则∠BAA'的度数是 °.?
12.
如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .?
13.如图所示,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针方向旋转一定的角度得到△ADE,当点B的对应点D恰好落在BC边上时,CD的长为 .?
14
如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为 .?
15
如图,在正方形网格中,格点三角形ABC绕某点顺时针旋转角α(0°<α<180°)得到格点三角形A1B1C1,点A与点A1、点B与点B1、点C与点C1是对应点,则α= 度.?
16.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长.
17.如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D.
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
18.如图,等腰三角形ABC绕顶点B逆时针旋转角α到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1,BC1分别交于点E,F.
(1)求证:△BCF≌△BA1D;
(2)当∠C=α时,判断四边形A1BCE的形状,并说明理由.
答案
1.D 2.A
3.D 4.D 5.D 6.D
7.(1)点B' (2)点O ∠AOA'或∠BOB'
(3)∠A' 线段OB'
8.AO=DO,BO=CO,AB=DC ∠AOD,∠BOC,∠BDC △ODC≌△OAB △AOD
9.A 60
10.150
11.65
12.15° .
13.1.6 .
14.3
15.90
16.解:∵将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,
∴AB=AD=1,∠BAD=∠CAE=90°,
∴BD==.
17.解:(1)证明:由旋转可知∠EAF=∠BAC,AF=AC,AE=AB,
∴∠EAF+∠BAF=∠BAC+∠BAF,
即∠BAE=∠CAF.
又∵AB=AC,∴AE=AF,
∴△ABE≌△ACF,∴BE=CF.
(2)∵四边形ACDE是菱形,AB=AC=1,
∴AC∥DE,DE=AE=AB=1.
又∵∠BAC=45°,
∴∠AEB=∠ABE=∠BAC=45°.
∵∠AEB+∠BAE+∠ABE=180°,
∴∠BAE=90°,
∴BE===,
∴BD=BE-DE=-1.
18.解:(1)证明:∵△ABC是等腰三角形,
∴AB=BC,∴∠A=∠C.
∵等腰三角形ABC绕顶点B逆时针旋转角α到△A1BC1的位置,
∴A1B=AB=BC,∠A1=∠A=∠C,∠ABC=∠A1BC1,
∴∠ABC-∠ABC1=∠A1BC1-∠ABC1,
即∠CBF=∠A1BD.
在△BCF与△BA1D中,
∴△BCF≌△BA1D.
(2)四边形A1BCE是菱形.理由:
∵∠C=α,∴∠A=∠A1=∠C1=α.
∵等腰三角形ABC绕顶点B逆时针旋转角α到△A1BC1的位置,
∴∠A1BA=∠C1BC=α,
∴∠A1BA=∠A,∠C1BC=∠C1,
∴A1B∥AC,A1C1∥BC,
∴四边形A1BCE是平行四边形.
又∵A1B=CB,
∴?A1BCE是菱形.
1.下列现象中是旋转的是( )
A.推拉抽屉
B.火车车厢的直线运动
C.电梯的上下移动
D.汽车方向盘的转动
2.将图按顺时针方向旋转90°后得到的图形是图中的( )
3
如图,E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为
( )
A.5
B.
C.7
D.
4
如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是
( )
A.AC=AD
B.AB⊥EB
C.BC=DE
D.∠A=∠EBC
5如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则点P'的坐标为
( )
A.(3,2)
B.(3,-1)
C.(2,-3)
D.(3,-2)
6
如图,△A'B'C'是由△ABC经过平移得到的,△A'B'C'还可以看作是由△ABC经过怎样的图形变化得到的?下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
A.①④
B.②③
C.②④
D.③④
7.如图所示,△AOB绕着点O顺时针旋转至△A'OB'的位置,此时:
(1)点B的对应点是 ;?
(2)旋转中心是 ,旋转角为 ;?
(3)∠A的对应角是 ,线段OB的对应线段是 .?
8.如图,△ODC是由△OAB绕点O顺时针旋转30°得到的图形,点D在线段AB上.图中相等的线段有 ;图中等于30°的角有 ;图中的全等三角形是 ;图中的等腰三角形是 .?
9.如图,△ABC是等边三角形,P是△ABC内一点.△APC沿顺时针方向旋转后与△AP'B重合,则旋转中心是点 ,旋转角等于 度.?
10.如图所示,将一个含30°角的三角尺ABC绕点A旋转,点C旋转后的对应点为C',要使点B,A,C'在同一条直线上,则三角尺ABC旋转的最小角度是 °.?
11.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到Rt△A'B'C,连接AA',若∠1=25°,则∠BAA'的度数是 °.?
12.
如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .?
13.如图所示,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针方向旋转一定的角度得到△ADE,当点B的对应点D恰好落在BC边上时,CD的长为 .?
14
如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为 .?
15
如图,在正方形网格中,格点三角形ABC绕某点顺时针旋转角α(0°<α<180°)得到格点三角形A1B1C1,点A与点A1、点B与点B1、点C与点C1是对应点,则α= 度.?
16.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长.
17.如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D.
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
18.如图,等腰三角形ABC绕顶点B逆时针旋转角α到△A1BC1的位置,AB与A1C1相交于点D,AC与A1C1,BC1分别交于点E,F.
(1)求证:△BCF≌△BA1D;
(2)当∠C=α时,判断四边形A1BCE的形状,并说明理由.
答案
1.D 2.A
3.D 4.D 5.D 6.D
7.(1)点B' (2)点O ∠AOA'或∠BOB'
(3)∠A' 线段OB'
8.AO=DO,BO=CO,AB=DC ∠AOD,∠BOC,∠BDC △ODC≌△OAB △AOD
9.A 60
10.150
11.65
12.15° .
13.1.6 .
14.3
15.90
16.解:∵将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,
∴AB=AD=1,∠BAD=∠CAE=90°,
∴BD==.
17.解:(1)证明:由旋转可知∠EAF=∠BAC,AF=AC,AE=AB,
∴∠EAF+∠BAF=∠BAC+∠BAF,
即∠BAE=∠CAF.
又∵AB=AC,∴AE=AF,
∴△ABE≌△ACF,∴BE=CF.
(2)∵四边形ACDE是菱形,AB=AC=1,
∴AC∥DE,DE=AE=AB=1.
又∵∠BAC=45°,
∴∠AEB=∠ABE=∠BAC=45°.
∵∠AEB+∠BAE+∠ABE=180°,
∴∠BAE=90°,
∴BE===,
∴BD=BE-DE=-1.
18.解:(1)证明:∵△ABC是等腰三角形,
∴AB=BC,∴∠A=∠C.
∵等腰三角形ABC绕顶点B逆时针旋转角α到△A1BC1的位置,
∴A1B=AB=BC,∠A1=∠A=∠C,∠ABC=∠A1BC1,
∴∠ABC-∠ABC1=∠A1BC1-∠ABC1,
即∠CBF=∠A1BD.
在△BCF与△BA1D中,
∴△BCF≌△BA1D.
(2)四边形A1BCE是菱形.理由:
∵∠C=α,∴∠A=∠A1=∠C1=α.
∵等腰三角形ABC绕顶点B逆时针旋转角α到△A1BC1的位置,
∴∠A1BA=∠C1BC=α,
∴∠A1BA=∠A,∠C1BC=∠C1,
∴A1B∥AC,A1C1∥BC,
∴四边形A1BCE是平行四边形.
又∵A1B=CB,
∴?A1BCE是菱形.
同课章节目录
