人教版八年级上册数学11.2.1 三角形的内角 课后作业(Word版 含答案)
文档属性
| 名称 | 人教版八年级上册数学11.2.1 三角形的内角 课后作业(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 358.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-17 00:00:00 | ||
图片预览



文档简介
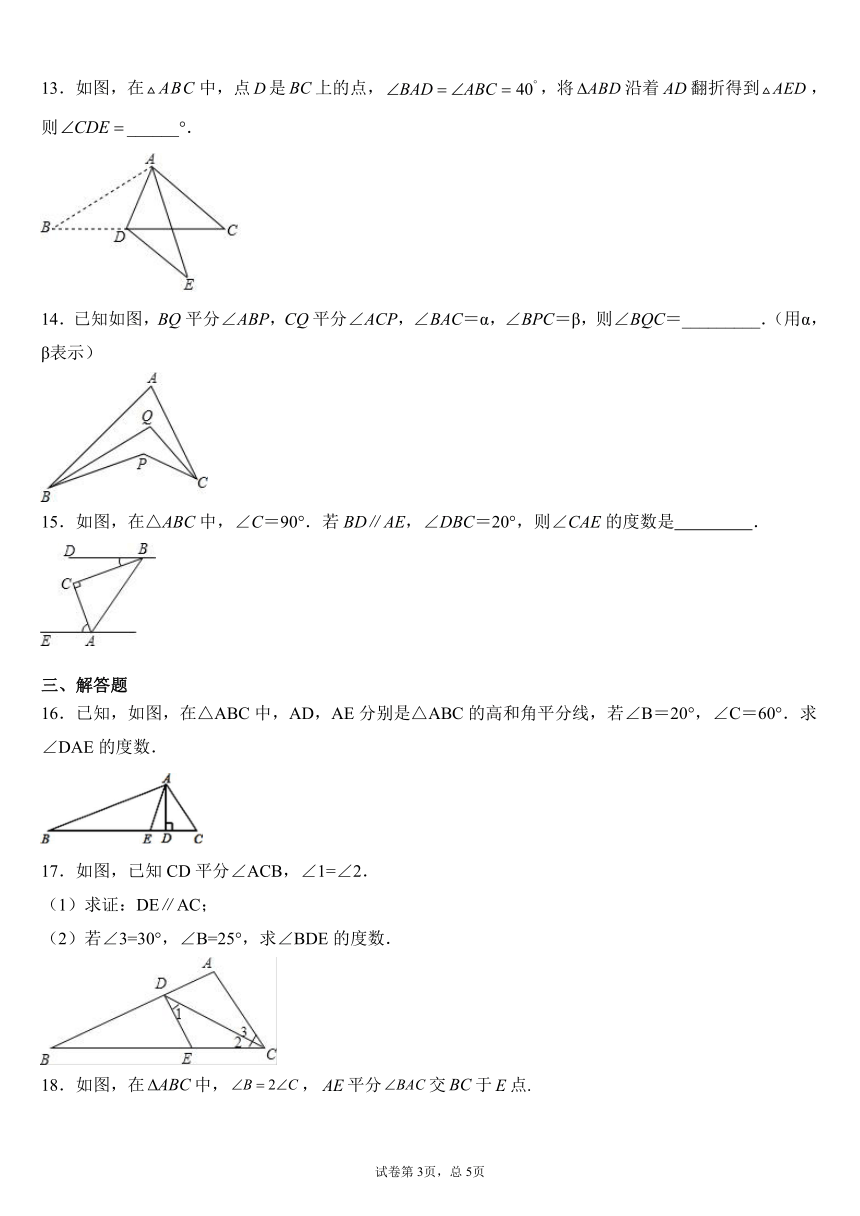
人教版八年级上册数学11.2.1
三角形的内角
课后作业
一、单选题
1.已知△ABC中,∠A=20°,∠B=70°,那么△ABC是( )
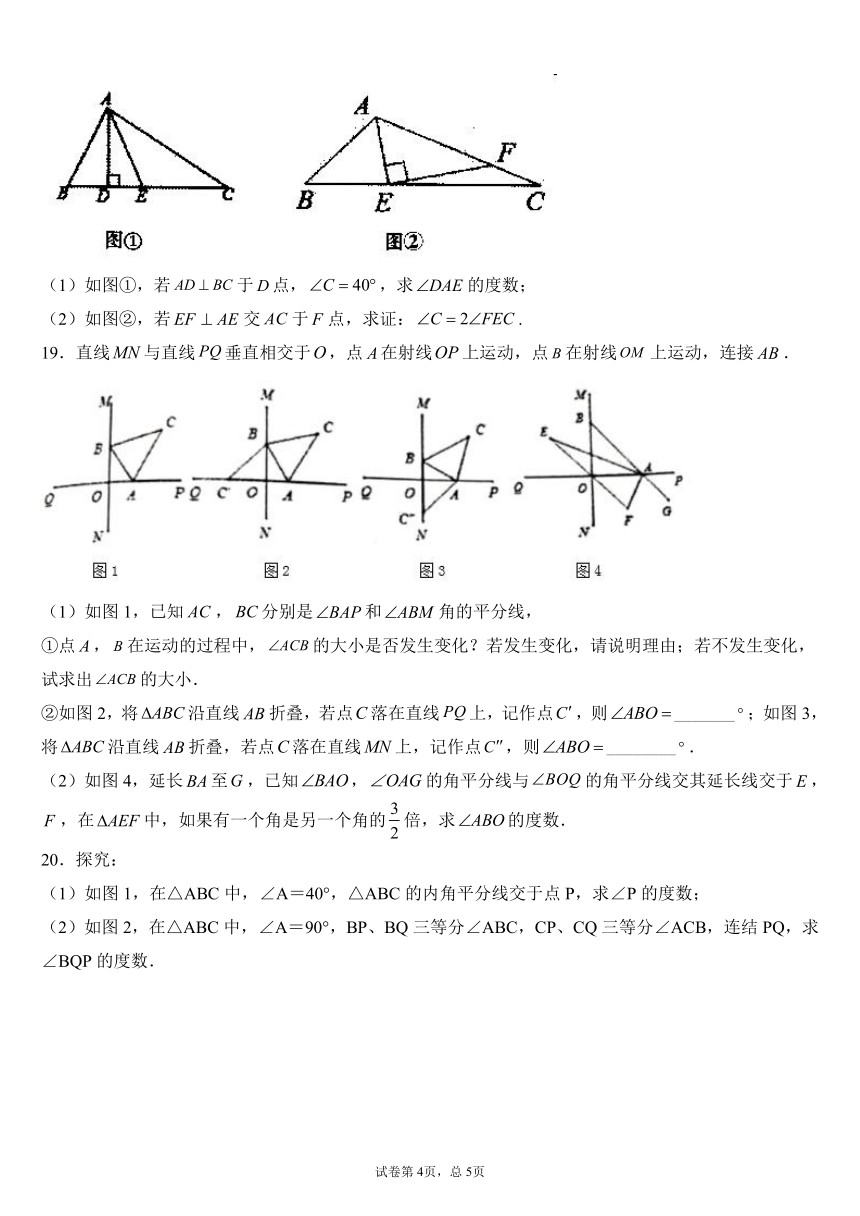
A.直角三角形
B.锐角三角形
C.钝角三角形
D.正三角形
2.若三角形三个内角度数比为2:3:4,则这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
3.下列条件中,能判定△ABC为直角三角形的是(
)
A.∠A=2∠B=3∠C
B.∠A+∠B=2∠C
C.∠A=∠B=30°
D.∠A=∠B=∠C
4.如图,中分别平分则的度数为(
)
A.
B.
C.
D.
5.一个缺角的三角形ABC残片如图所示,量得∠A=60°,∠B=75°,则这个三角形残缺前的∠C的度数为( )
A.75°
B.60°
C.45°
D.40°
6.如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数(
)
A.24°
B.25°
C.30°
D.35°
7.如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=65°,则∠2的度数为(
)
A.
B.
C.
D.
8.如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=50°,则∠ABD+∠ACD的值为( )
A.60°
B.50°
C.40°
D.30°
9.如图,在中,,与的平分线交于点,得;与的平分线相交于点,得;……;与的平分线交于点,要使的度数为整数,则的最大值为(
)
A.4
B.5
C.6
D.7
二、填空题
10.直角三角形中,一个锐角等于另一个锐角的2倍,则较小的锐角是_______.
11.如图,∠1+∠2+∠3+∠4=______度.
12.如图,在中,是边上的高,平分,若,,则__________.
13.如图,在中,点是上的点,,将沿着翻折得到,则______°.
14.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=_________.(用α,β表示)
15.如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是
.
三、解答题
16.已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=20°,∠C=60°.求∠DAE的度数.
17.如图,已知CD平分∠ACB,∠1=∠2.
(1)求证:DE∥AC;
(2)若∠3=30°,∠B=25°,求∠BDE的度数.
18.如图,在中,,平分交于点.
(1)如图①,若于点,,求的度数;
(2)如图②,若交于点,求证:.
19.直线与直线垂直相交于,点在射线上运动,点在射线上运动,连接.
(1)如图1,已知,分别是和角的平分线,
①点,在运动的过程中,的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出的大小.
②如图2,将沿直线折叠,若点落在直线上,记作点,则_______;如图3,将沿直线折叠,若点落在直线上,记作点,则________.
(2)如图4,延长至,已知,的角平分线与的角平分线交其延长线交于,,在中,如果有一个角是另一个角的倍,求的度数.
20.探究:
(1)如图1,在△ABC中,∠A=40°,△ABC的内角平分线交于点P,求∠P的度数;
(2)如图2,在△ABC中,∠A=90°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB,连结PQ,求∠BQP的度数.
试卷第4页,总5页
试卷第1页,总5页
答案
1.A
2.A
3.D
4.C
5.C
6.D
7.B
8.C
9.C
10.30°
11.280
12.50°
13.20
14.(α+β).
15.70°
16.解:在△ABC中,
∵∠B=20°,∠C=60°
∴∠BAC=180°﹣∠B﹣∠C
=180°﹣20°﹣60°
=100°
∵AE是的角平分线,
∴∠EAC=∠BAC
=×100°
=50°,
∵AD是△ABC的高,
∴∠ADC=90°
∴∠DAC=180°﹣∠ADC﹣∠C
=180°﹣90°﹣60°
=30°,
∴∠DAE=∠EAC﹣∠DAC
=50°﹣30°
=20°.
17.(1)证明:∵CD平分∠ACB,
∴∠2=∠3.
∵∠1=∠2,
∴∠1=∠3,
∴DE∥AC;
(2)解:∵CD平分∠ACB,∠3=30°,
∴∠ACB=2∠3=60°.
∵DE∥AC,
∴∠BED=∠ACB=60°.
∵∠B=25°,
∴∠BDE=180°-60°-25°=95°.
18.(1)解:∵∠C=40°,∠B=2∠C,
∴∠B=80°,
∴∠BAC=60°,
∵AE平分∠BAC,
∴∠EAC=30°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=50°,
∴∠DAE=50°?30°=20°;
(2)证明:作AD⊥BC
于D点,如图,∵EF⊥AE,
∴∠AEF=90°,
∴∠AED+∠FEC=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠FEC,
∵AE平分∠BAC,
∴∠EAC=∠BAC=(180°?∠B?∠C)=(180°?3∠C)=90°?∠C,
∵∠DAE=∠DAC?∠EAC,
∴∠DAE=∠DAC?(90°?∠C)=90°?∠C?90°+∠C=∠C,
∴∠FEC=∠C,
∴∠C=2∠FEC.
19.(1)①∠ACB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠ABM=270°,
∵AC、BC分别是∠BAP和∠ABM角的平分线,
∴∠BAC=∠PAB,∠ABC=∠ABM,
∴∠BAC+∠ABC=(∠PAB+∠ABM)=135°,
∴∠ACB=45°;
②∵图2中,将△ABC沿直线AB折叠,若点C落在直线PQ上,
∴∠CAB=∠BAQ,
∵AC平分∠PAB,
∴∠PAC=∠CAB,
∴∠PAC=∠CAB=∠BAO=60°,
∵∠AOB=90°,
∴∠ABO=30°,
∵图3中,将△ABC沿直线AB折叠,若点C落在直线MN上,
∴∠ABC=∠ABN,
∵BC平分∠ABM,
∴∠ABC=∠MBC,
∴∠MBC=∠ABC=∠ABN,
∴∠ABO=60°,
(2)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=∠BAO,∠EOQ=∠BOQ,
∴∠E=∠EOQ-∠EAO=(∠BOQ-∠BAO)=∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.
在△AEF中,
∵有一个角是另一个角的倍,故有:
①∠EAF=∠E,∠E=60°,∠ABO=120°(不合题意,舍去);
②∠EAF=∠F,∠E=30°,∠ABO=60°;
③∠F=∠E,∠E=36°,∠ABO=72°;
④∠E=∠F,∠E=54°,∠ABO=108°(不合题意,舍去);.
∴∠ABO为60°或72°.
20.解:(1)∵∠A+∠ABC+∠ACB
=
180°
∴∠ABC+∠ACB=180°
-∠A
=140°
∵BP平分∠ABC,
CP平分∠ACB
∴
∠PBC+∠PCB=(
∠ABC+∠ACB
)=70°
∵∠P+∠PBC+∠PCB
=
180°
∴∠P=180°-(∠PBC+∠PCB)=110°
(2)∵∠A+∠ABC+
∠ACB
=
180°
∴∠ABC+∠ACB=180°
-∠A
=90°
∵BQ三等分∠ABC,CQ三等分∠ACB
∴
∠QBC+∠QCB=(
∠ABC+∠ACB
)=60°
∵∠Q+∠QBC+∠QCB=
180°
∴∠Q=180°-(∠QBC+∠QCB)=120°
∵BP平分∠QBC,
CP平分∠QCB
∴PQ平分∠BQC
∴∠BQP
=×120°=60°
三角形的内角
课后作业
一、单选题
1.已知△ABC中,∠A=20°,∠B=70°,那么△ABC是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.正三角形
2.若三角形三个内角度数比为2:3:4,则这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
3.下列条件中,能判定△ABC为直角三角形的是(
)
A.∠A=2∠B=3∠C
B.∠A+∠B=2∠C
C.∠A=∠B=30°
D.∠A=∠B=∠C
4.如图,中分别平分则的度数为(
)
A.
B.
C.
D.
5.一个缺角的三角形ABC残片如图所示,量得∠A=60°,∠B=75°,则这个三角形残缺前的∠C的度数为( )
A.75°
B.60°
C.45°
D.40°
6.如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数(
)
A.24°
B.25°
C.30°
D.35°
7.如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=65°,则∠2的度数为(
)
A.
B.
C.
D.
8.如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=50°,则∠ABD+∠ACD的值为( )
A.60°
B.50°
C.40°
D.30°
9.如图,在中,,与的平分线交于点,得;与的平分线相交于点,得;……;与的平分线交于点,要使的度数为整数,则的最大值为(
)
A.4
B.5
C.6
D.7
二、填空题
10.直角三角形中,一个锐角等于另一个锐角的2倍,则较小的锐角是_______.
11.如图,∠1+∠2+∠3+∠4=______度.
12.如图,在中,是边上的高,平分,若,,则__________.
13.如图,在中,点是上的点,,将沿着翻折得到,则______°.
14.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=_________.(用α,β表示)
15.如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是
.
三、解答题
16.已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=20°,∠C=60°.求∠DAE的度数.
17.如图,已知CD平分∠ACB,∠1=∠2.
(1)求证:DE∥AC;
(2)若∠3=30°,∠B=25°,求∠BDE的度数.
18.如图,在中,,平分交于点.
(1)如图①,若于点,,求的度数;
(2)如图②,若交于点,求证:.
19.直线与直线垂直相交于,点在射线上运动,点在射线上运动,连接.
(1)如图1,已知,分别是和角的平分线,
①点,在运动的过程中,的大小是否发生变化?若发生变化,请说明理由;若不发生变化,试求出的大小.
②如图2,将沿直线折叠,若点落在直线上,记作点,则_______;如图3,将沿直线折叠,若点落在直线上,记作点,则________.
(2)如图4,延长至,已知,的角平分线与的角平分线交其延长线交于,,在中,如果有一个角是另一个角的倍,求的度数.
20.探究:
(1)如图1,在△ABC中,∠A=40°,△ABC的内角平分线交于点P,求∠P的度数;
(2)如图2,在△ABC中,∠A=90°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB,连结PQ,求∠BQP的度数.
试卷第4页,总5页
试卷第1页,总5页
答案
1.A
2.A
3.D
4.C
5.C
6.D
7.B
8.C
9.C
10.30°
11.280
12.50°
13.20
14.(α+β).
15.70°
16.解:在△ABC中,
∵∠B=20°,∠C=60°
∴∠BAC=180°﹣∠B﹣∠C
=180°﹣20°﹣60°
=100°
∵AE是的角平分线,
∴∠EAC=∠BAC
=×100°
=50°,
∵AD是△ABC的高,
∴∠ADC=90°
∴∠DAC=180°﹣∠ADC﹣∠C
=180°﹣90°﹣60°
=30°,
∴∠DAE=∠EAC﹣∠DAC
=50°﹣30°
=20°.
17.(1)证明:∵CD平分∠ACB,
∴∠2=∠3.
∵∠1=∠2,
∴∠1=∠3,
∴DE∥AC;
(2)解:∵CD平分∠ACB,∠3=30°,
∴∠ACB=2∠3=60°.
∵DE∥AC,
∴∠BED=∠ACB=60°.
∵∠B=25°,
∴∠BDE=180°-60°-25°=95°.
18.(1)解:∵∠C=40°,∠B=2∠C,
∴∠B=80°,
∴∠BAC=60°,
∵AE平分∠BAC,
∴∠EAC=30°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=50°,
∴∠DAE=50°?30°=20°;
(2)证明:作AD⊥BC
于D点,如图,∵EF⊥AE,
∴∠AEF=90°,
∴∠AED+∠FEC=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠FEC,
∵AE平分∠BAC,
∴∠EAC=∠BAC=(180°?∠B?∠C)=(180°?3∠C)=90°?∠C,
∵∠DAE=∠DAC?∠EAC,
∴∠DAE=∠DAC?(90°?∠C)=90°?∠C?90°+∠C=∠C,
∴∠FEC=∠C,
∴∠C=2∠FEC.
19.(1)①∠ACB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠ABM=270°,
∵AC、BC分别是∠BAP和∠ABM角的平分线,
∴∠BAC=∠PAB,∠ABC=∠ABM,
∴∠BAC+∠ABC=(∠PAB+∠ABM)=135°,
∴∠ACB=45°;
②∵图2中,将△ABC沿直线AB折叠,若点C落在直线PQ上,
∴∠CAB=∠BAQ,
∵AC平分∠PAB,
∴∠PAC=∠CAB,
∴∠PAC=∠CAB=∠BAO=60°,
∵∠AOB=90°,
∴∠ABO=30°,
∵图3中,将△ABC沿直线AB折叠,若点C落在直线MN上,
∴∠ABC=∠ABN,
∵BC平分∠ABM,
∴∠ABC=∠MBC,
∴∠MBC=∠ABC=∠ABN,
∴∠ABO=60°,
(2)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=∠BAO,∠EOQ=∠BOQ,
∴∠E=∠EOQ-∠EAO=(∠BOQ-∠BAO)=∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.
在△AEF中,
∵有一个角是另一个角的倍,故有:
①∠EAF=∠E,∠E=60°,∠ABO=120°(不合题意,舍去);
②∠EAF=∠F,∠E=30°,∠ABO=60°;
③∠F=∠E,∠E=36°,∠ABO=72°;
④∠E=∠F,∠E=54°,∠ABO=108°(不合题意,舍去);.
∴∠ABO为60°或72°.
20.解:(1)∵∠A+∠ABC+∠ACB
=
180°
∴∠ABC+∠ACB=180°
-∠A
=140°
∵BP平分∠ABC,
CP平分∠ACB
∴
∠PBC+∠PCB=(
∠ABC+∠ACB
)=70°
∵∠P+∠PBC+∠PCB
=
180°
∴∠P=180°-(∠PBC+∠PCB)=110°
(2)∵∠A+∠ABC+
∠ACB
=
180°
∴∠ABC+∠ACB=180°
-∠A
=90°
∵BQ三等分∠ABC,CQ三等分∠ACB
∴
∠QBC+∠QCB=(
∠ABC+∠ACB
)=60°
∵∠Q+∠QBC+∠QCB=
180°
∴∠Q=180°-(∠QBC+∠QCB)=120°
∵BP平分∠QBC,
CP平分∠QCB
∴PQ平分∠BQC
∴∠BQP
=×120°=60°
