人教版八年级上册数学11.2.2三角形的外角课件(共22张PPT)
文档属性
| 名称 | 人教版八年级上册数学11.2.2三角形的外角课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1004.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 10:00:29 | ||
图片预览




文档简介
(共22张PPT)
11.2.2
三角形的外角
【学习目标】
1、了解三角形的外角的性质,能用学过的定理论证这些性质。
2、能利用三角形的外角性质解决问题。
【预习导学】
自学课本P14-P15页,完成下列问题:
1、什么叫做三角形的外角?
2、三角形的一个顶点处有几个外角?
3、三角形的一个外角和与它相邻的内角有什么关系?
4、你能证明三角形一个外角与它不相邻的两个内角有什么关系吗?
5、试着完成15页“练习”。
A
B
C
D
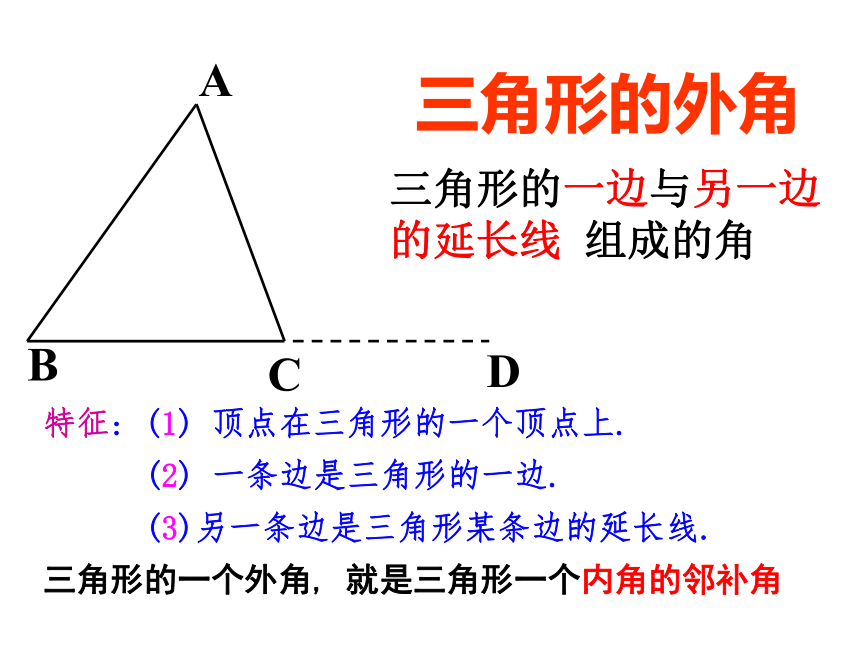
三角形的外角
三角形的一边与另一边
的延长线
组成的角
特征:
(1)
顶点在三角形的一个顶点上.
(2)
一条边是三角形的一边.
(3)另一条边是三角形某条边的延长线.
三角形的一个外角,
就是三角形一个内角的邻补角
C
A
B
D
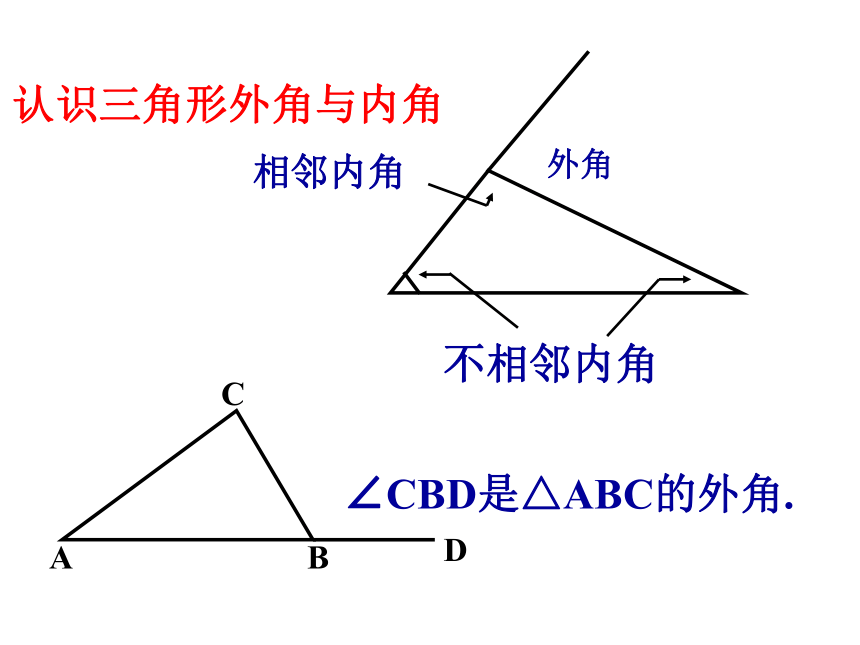
外角
相邻内角
不相邻内角
∠CBD是△ABC的外角.
认识三角形外角与内角
A
B
C
想一想△ABC的外角共有几个呢?
1、每一个三角形都有6个外角.
2、每一个顶点相对应的外角都有2个,它们相等.
A
B
C
D
E
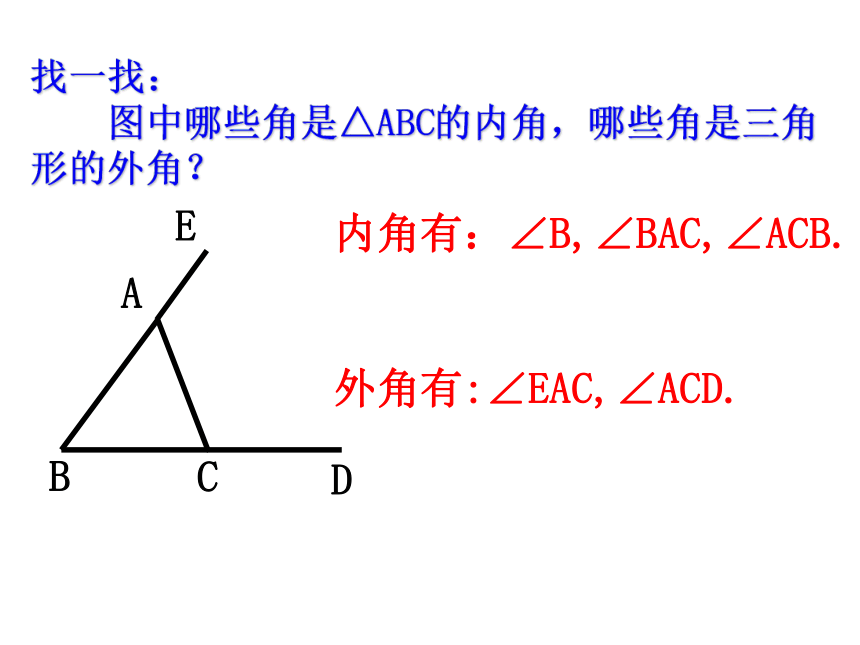
找一找:
图中哪些角是△ABC的内角,哪些角是三角形的外角?
内角有:∠B,∠BAC,∠ACB.
外角有:∠EAC,∠ACD.
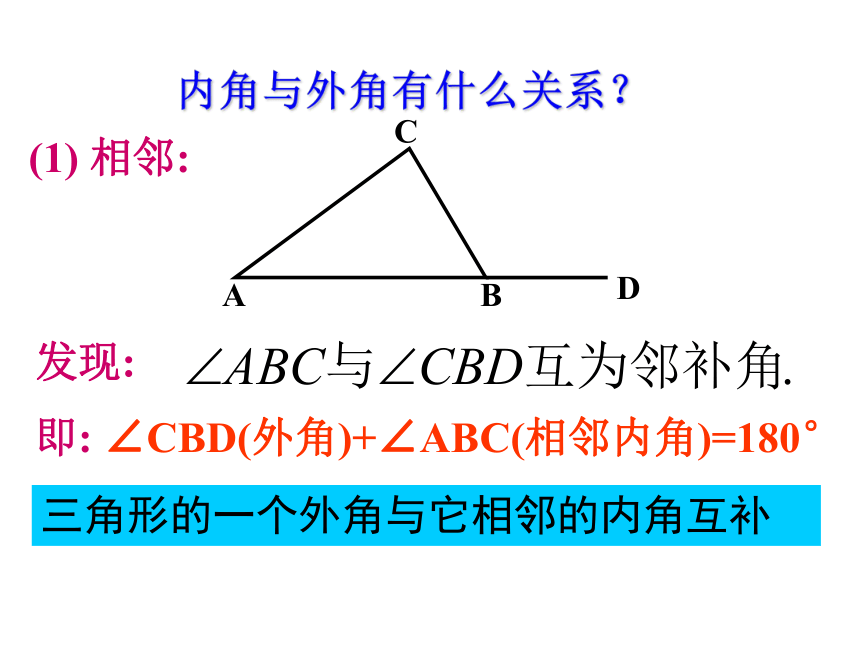
内角与外角有什么关系?
(1)
相邻:
C
A
B
D
发现:
即:
∠CBD(外角)+∠ABC(相邻内角)=180°
三角形的一个外角与它相邻的内角互补
C
A
B
D
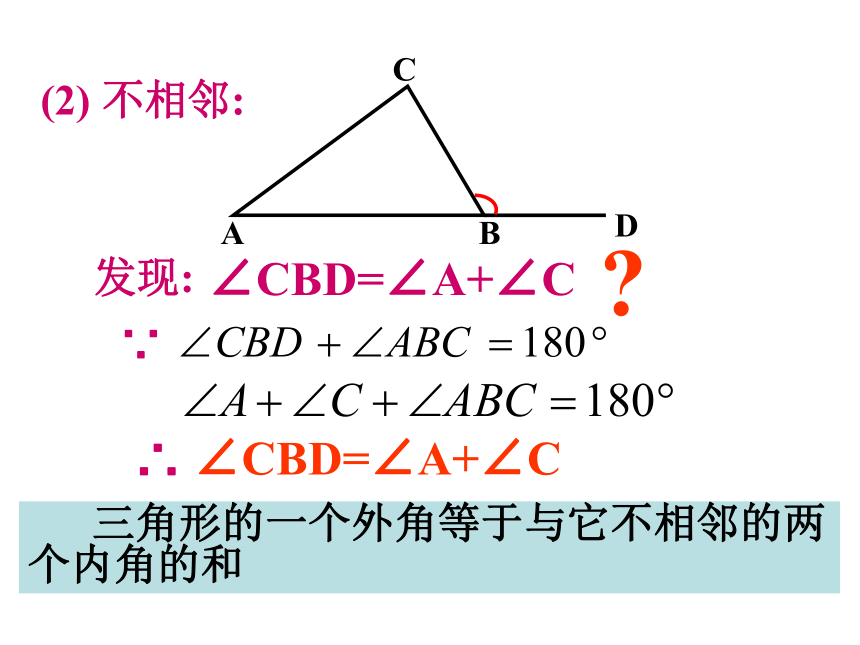
(2)
不相邻:
?
∵
∴
∠CBD=∠A+∠C
发现:
∠CBD=∠A+∠C
三角形的一个外角等于与它不相邻的两个内角的和
三角形内角和定理的推论:
三角形的外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论.和定理一样,推论可以作为进一步推理的依据.
1.如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
则(1)∠B=
;
(2)∠C=
.
A
B
C
D
80°
70°
40°
试一试1:
70°
上面我们通过计算得到了三角形中外角与不相邻两内角之间的数量关系.你能填写下面关系吗?
议一议
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>)
三角形的一个外角大于任何一个与它不相邻的内角。
A
C
B
D
>
>
三角形的外角和
如图,
∠BAE,
∠CBF,
∠ACD是△ABC的三个外角,它们的和是多少?
解:
∵△ABC中
∠BAE=
∠2+
∠3,
∠CBF=
∠1+
∠3,
∠ACD=
∠1+
∠2.
又∵∠1+
∠2+
∠3=180
°,
∴∠BAE+
∠CBF+
∠ACD=2(∠1+
∠2+
∠3)=360
°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
三角形的外角和等于360°
1、判断题:
1①.三角形的外角和是指三角形所有外角的和.(
)
2.三角形的外角和等于它内角和的2倍.(
)
3.三角形的一个外角等于两个内角的和.(
)
A
B
C
D
E
F
1
H
2
【例】已知:国旗上的一个五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
【解析】设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
1.已知△ABC的一个外角为50°,则△ABC一定是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.钝角三角形或锐角三角形
B
2.
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B=
.
70°
3.
一副三角板,如图叠放在一起,∠1的度数是_______度.
75
4.已知图中∠A,∠B,∠C分别为80°,20°,30°,则∠1=
.
B
3
2
1
A
C
D
E
130°
5.如图,∠A+∠B+∠C+∠D+∠E+∠F=
.
1
2
3
360°
A
B
C
D
E
F
6、如图,∠A=50°,∠B=40°,∠C=30°,求∠BPC的度数。
解:连接AP并延长到点E
∵∠BPE=∠B+∠BAP,
∠CPE=∠C+∠CAP
又∵∠BPC=∠BPE+∠CPE
∴∠BPC=∠B+∠BAP+∠C+∠CAP
=∠BAC+∠B+∠C
=50°+40°+30°
=120°
A
B
C
P
E
1.三角形内角和定理的推论:
三角形的外角等于与它不相邻的两个内角的和.
2.三角形的外角和是360°.
通过本课时的学习,需要我们掌握:
作业布置
课本16页,第5题
17页,第6题
11.2.2
三角形的外角
【学习目标】
1、了解三角形的外角的性质,能用学过的定理论证这些性质。
2、能利用三角形的外角性质解决问题。
【预习导学】
自学课本P14-P15页,完成下列问题:
1、什么叫做三角形的外角?
2、三角形的一个顶点处有几个外角?
3、三角形的一个外角和与它相邻的内角有什么关系?
4、你能证明三角形一个外角与它不相邻的两个内角有什么关系吗?
5、试着完成15页“练习”。
A
B
C
D
三角形的外角
三角形的一边与另一边
的延长线
组成的角
特征:
(1)
顶点在三角形的一个顶点上.
(2)
一条边是三角形的一边.
(3)另一条边是三角形某条边的延长线.
三角形的一个外角,
就是三角形一个内角的邻补角
C
A
B
D
外角
相邻内角
不相邻内角
∠CBD是△ABC的外角.
认识三角形外角与内角
A
B
C
想一想△ABC的外角共有几个呢?
1、每一个三角形都有6个外角.
2、每一个顶点相对应的外角都有2个,它们相等.
A
B
C
D
E
找一找:
图中哪些角是△ABC的内角,哪些角是三角形的外角?
内角有:∠B,∠BAC,∠ACB.
外角有:∠EAC,∠ACD.
内角与外角有什么关系?
(1)
相邻:
C
A
B
D
发现:
即:
∠CBD(外角)+∠ABC(相邻内角)=180°
三角形的一个外角与它相邻的内角互补
C
A
B
D
(2)
不相邻:
?
∵
∴
∠CBD=∠A+∠C
发现:
∠CBD=∠A+∠C
三角形的一个外角等于与它不相邻的两个内角的和
三角形内角和定理的推论:
三角形的外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论.和定理一样,推论可以作为进一步推理的依据.
1.如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
则(1)∠B=
;
(2)∠C=
.
A
B
C
D
80°
70°
40°
试一试1:
70°
上面我们通过计算得到了三角形中外角与不相邻两内角之间的数量关系.你能填写下面关系吗?
议一议
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>)
三角形的一个外角大于任何一个与它不相邻的内角。
A
C
B
D
>
>
三角形的外角和
如图,
∠BAE,
∠CBF,
∠ACD是△ABC的三个外角,它们的和是多少?
解:
∵△ABC中
∠BAE=
∠2+
∠3,
∠CBF=
∠1+
∠3,
∠ACD=
∠1+
∠2.
又∵∠1+
∠2+
∠3=180
°,
∴∠BAE+
∠CBF+
∠ACD=2(∠1+
∠2+
∠3)=360
°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
三角形的外角和等于360°
1、判断题:
1①.三角形的外角和是指三角形所有外角的和.(
)
2.三角形的外角和等于它内角和的2倍.(
)
3.三角形的一个外角等于两个内角的和.(
)
A
B
C
D
E
F
1
H
2
【例】已知:国旗上的一个五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
【解析】设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
1.已知△ABC的一个外角为50°,则△ABC一定是(
)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.钝角三角形或锐角三角形
B
2.
如图,在△ABC中,∠A=80°,点D是BC延长线上一点,∠ACD=150°,则∠B=
.
70°
3.
一副三角板,如图叠放在一起,∠1的度数是_______度.
75
4.已知图中∠A,∠B,∠C分别为80°,20°,30°,则∠1=
.
B
3
2
1
A
C
D
E
130°
5.如图,∠A+∠B+∠C+∠D+∠E+∠F=
.
1
2
3
360°
A
B
C
D
E
F
6、如图,∠A=50°,∠B=40°,∠C=30°,求∠BPC的度数。
解:连接AP并延长到点E
∵∠BPE=∠B+∠BAP,
∠CPE=∠C+∠CAP
又∵∠BPC=∠BPE+∠CPE
∴∠BPC=∠B+∠BAP+∠C+∠CAP
=∠BAC+∠B+∠C
=50°+40°+30°
=120°
A
B
C
P
E
1.三角形内角和定理的推论:
三角形的外角等于与它不相邻的两个内角的和.
2.三角形的外角和是360°.
通过本课时的学习,需要我们掌握:
作业布置
课本16页,第5题
17页,第6题
