人教版八年级数学(五四制)下册期末综合复习题(三)(word版,含答案)
文档属性
| 名称 | 人教版八年级数学(五四制)下册期末综合复习题(三)(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 427.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-17 20:11:19 | ||
图片预览


文档简介
综合复习题(三)
一、选择题(每小题3分,共计30分)
1.下列方程是一元二次方程的是(
)
A.x+2y=l
B.x+5=0
C.x+=8
D.3x+8=6x+2
2.正比例函数y=kx的图象经过点(1,2),则k的值为(
)
A.
-
B.
-2
C.
D.2
3.下列四条四组线段中,可以构成直角三角形的是(
)
A.
1,4,9
B.
5,6,7
C.5,12,13
D.
5,11,l2
4.一元二次方程x+x-4=0的根的情况是(
)
A.有两个相等的实数根
B.有两个不相等的实数根
C.没有实数根
D.只有一个实数根
5.一条长64厘米的铁丝被剪成两段,每段均折成正方形,且两个正方形的面积之差为160cm,若设较小的正方形的边长为xcm,则可列方程(
)
A.(16-x)-x=160
B.(64-x)-x=160
C.
x-(16-x)=160
D.(64-x)-x=160
6.对于函数y=-3x+1,下列结论结论正确的是(
)
A.它的图像必经过点(-l,3)
B.它的图经过第一、二、三象限
C.当x>时,yD.y的值随着x的增大而增大
7.如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使A的对应点A'落在对角线BD上,折痕为DG,则AG的长为
(
)
A.
1
B.
C.
D.
2
8.下列命题中,真命题的是(
)
A.一组对边平行,一组对角相等的四边形是平行四边形
B.两条对角线相等的四边形是矩形
C.一条对角线平分一组对角的四边形是菱形
D.四条边相等的四边形是正方形
9.菱形的周长为16厘米,两相邻角度数比是1:2,菱形的面积是(
)平方厘米
A.8
B.8
C.16
D.16
10.甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲、乙两人相距s(米),甲行走的时间为t(分)s关于t的函数图像的一部分如图所示,下列四种说法中:①甲行走的速度为30米/分;②乙出发l2.5分钟时追上甲;③当t=35时,a=450;④甲行走30.5分或38分时.甲、乙两人相距360米.其中正确的个数有(
).
A.11个
B.24个
C.3个
D.4个
二、填空题(每小题3分,共计30分)
11.函数y=中,自变量x的取值范围是
.
12.命题“如果两个实数相等,那么它们的平方相等”的逆命题是
.(填“真命题”或“假命题”)
13.已知m是是方程x-x-=0的一个根,则
m-m的值是
.
14.在Rt△ABC中,斜边AB=2,则
AB+BC+AC=
.
15.如图,在△ABC中,D、E分别是AB、AC的中点,若BC=10.则DE=
.
16.公司4月份利润为160万元.要使6月份的利润达到250万元,则平均每月增长的百分率是
.
17.如图,直线∥,平行四边形ABCD的面积为8,点E是直线上任意一点,连接BE、CE,则△EBC三角形的面积是
.
18.三角形的边长分别为3和5,要使这个三角形是直角三角形,则第三边长是
.
19.如图,函数y=-2x和y=kx+b图象相交于点A(m,3),关于x的不等式kx+b+2x>0的解集为
.
20.如图,四边形ABCD中,∠BAD=105°,∠ADC=120°,E是AD的中点,BE⊥EC,若AB=3,CD=,则BC=_________
三、解答题(共计60分)
21.解方程:
(1)
(2)
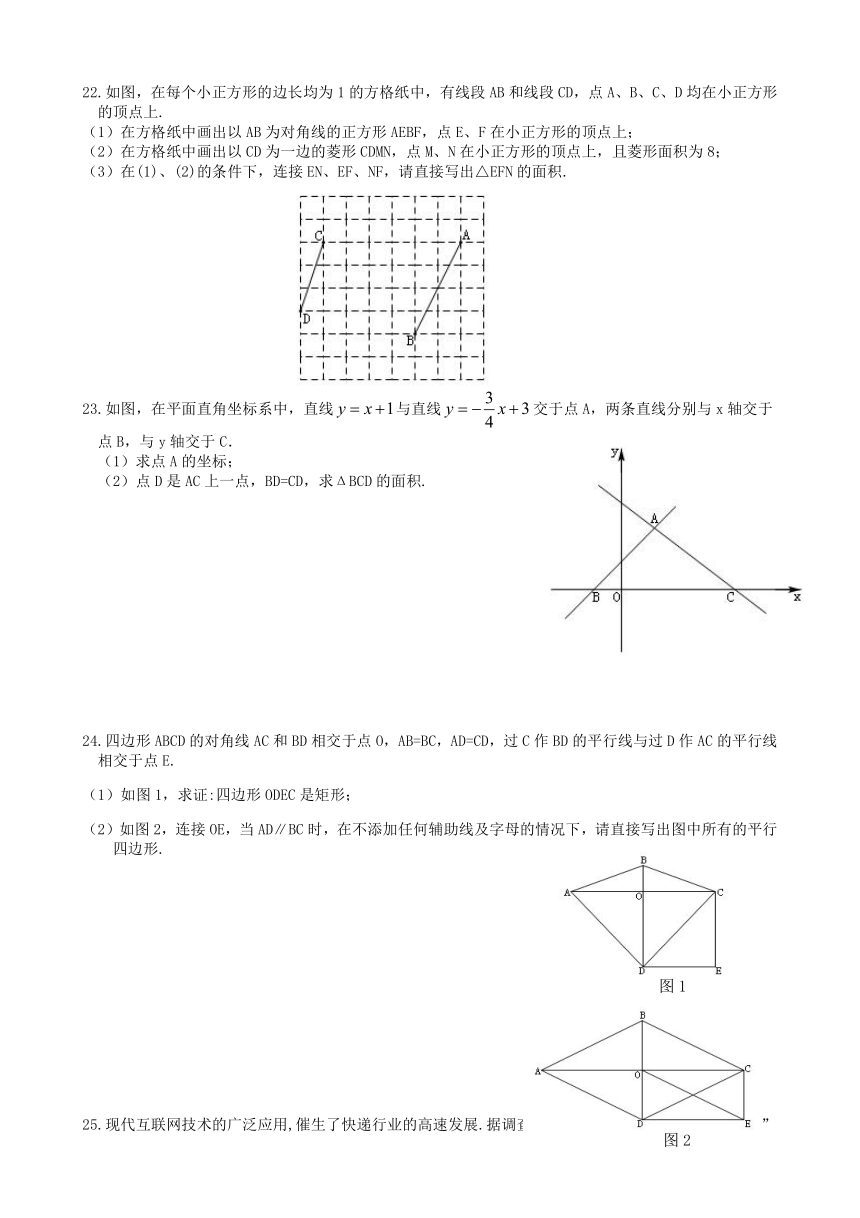
22.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画出以AB为对角线的正方形AEBF,点E、F在小正方形的顶点上;
(2)在方格纸中画出以CD为一边的菱形CDMN,点M、N在小正方形的顶点上,且菱形面积为8;
(3)在(1)、(2)的条件下,连接EN、EF、NF,请直接写出△EFN的面积.
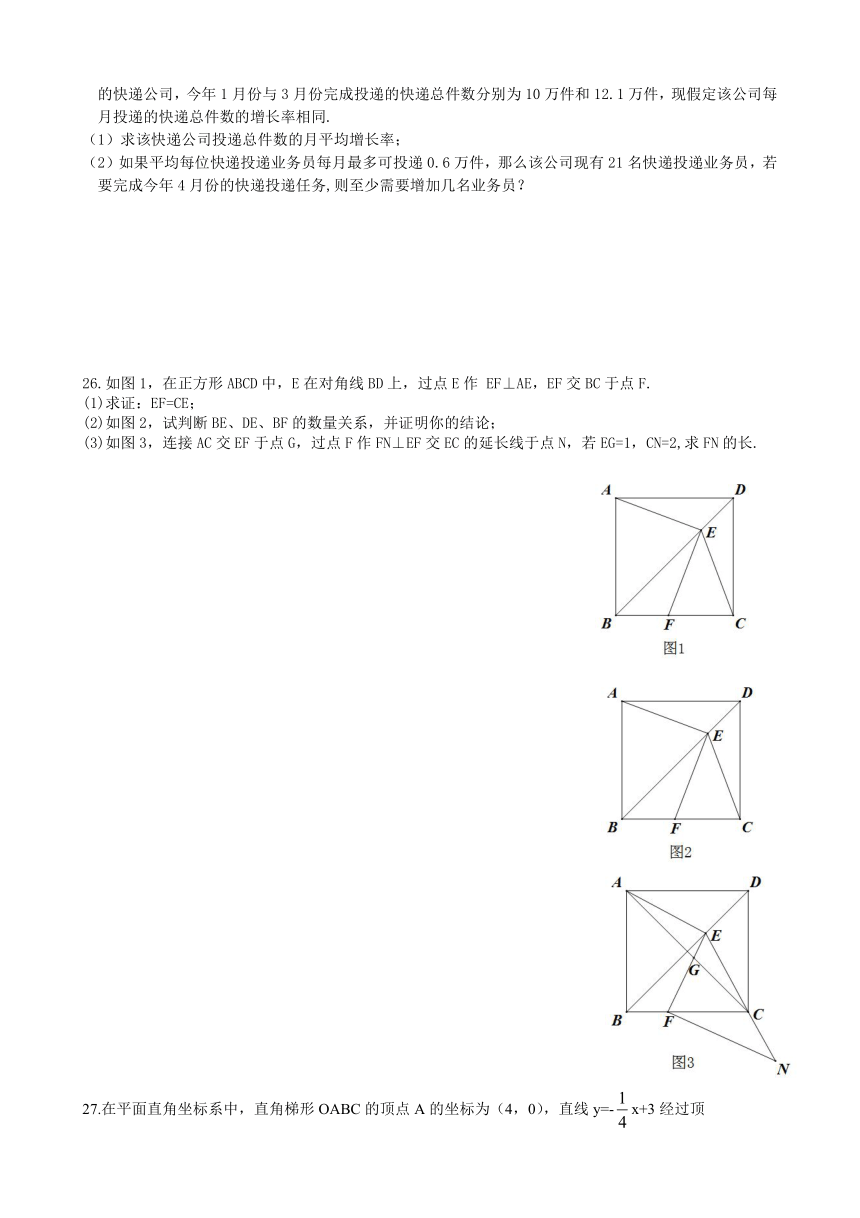
23.如图,在平面直角坐标系中,直线与直线交于点A,两条直线分别与x轴交于点B,与y轴交于C.
(1)求点A的坐标;
(2)点D是AC上一点,BD=CD,求ΔBCD的面积.
24.四边形ABCD的对角线AC和BD相交于点O,AB=BC,AD=CD,过C作BD的平行线与过D作AC的平行线相交于点E.
(1)如图1,求证:四边形ODEC是矩形;
(2)如图2,连接OE,当AD∥BC时,在不添加任何辅助线及字母的情况下,请直接写出图中所有的平行四边形.
25.现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,哈市某家小型“大学生自主创业”的快递公司,今年1月份与3月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每位快递投递业务员每月最多可投递0.6万件,那么该公司现有21名快递投递业务员,若要完成今年4月份的快递投递任务,则至少需要增加几名业务员?
26.如图1,在正方形ABCD中,E在对角线BD上,过点E作
EF⊥AE,EF交BC于点F.
(1)求证:EF=CE;
(2)如图2,试判断BE、DE、BF的数量关系,并证明你的结论;
(3)如图3,连接AC交EF于点G,过点F作FN⊥EF交EC的延长线于点N,若EG=1,CN=2,求FN的长.
27.在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4,0),直线y=-x+3经过顶
点B,与y轴交于顶点C,AB∥OC.
(1)如图1,求顶点B的坐标;
(2)如图2,直线l经过点C,与直线AB交于点M,点O′为点O关于直线l的对称点,连接CO′,并延长交直线AB于第一象限的点D,当CD=5时,求直线l的解析式;
(3)在(2)的条件下,点P在直线l上运动,点Q在直线OD上运动,以P、Q、B、C为顶点的四边形能否成为平行四边形?若能,求出点P的坐标;若不能,说明理由.
综合复习题(三)
选择题
A
2.
D
3.
C
4.
B
5.
A
6.
C
7.
C
8.
A
9.B
10.C
二、填空题
11.x≠-4
12.
假命题
13.
14.
8
15.
5
16.25%
17.
4
18.
4或
19.x<
20.
三、解答题
21.,
,
22.
答案:(1)如图
(2)如图
(3)如图,=4.
23.解:(1)联立方程
解得:
∴点A的坐标为(,)
直线y=x+1令y=0,x=-1,∴B(-1,0)
直线y=-x+3
令y=0,x=4
∴C(4,0)
过点D作DE⊥x轴于点E
∵DB=DC
∴BE=CE=BC=
易得E(,0)
将x=代入中
y=
∴D(,)
SΔBCD=BC?DE=×5×=
24.(1)证明:∵CE∥BD,DE∥AC
∴四边形ODEC是平行四边形
∵AB=BC,AD=CD,BD=BD
∴△ABD≌△CBD
∴∠ABD=∠CBO
∵AB=BC
∴∠BAO=∠BCO
∴∠AOB=∠BOC.
∵∠AOB+∠BOC=180°,
∴∠AOB=∠BOC=90°
∴∠COD=90°
∴四边形ODEC是矩形
(2)□ABCD,□ODEC,□OBCE,□ADEO
25.解:(1)设该快递公司投递总件数的月平均增长车为x.
根据题意,得10(1+x)2=12.1,
解得:x1=0.1,x2=-2.1(舍去)
答:该快递公司授递总件数的月平均增长率为10%.
(2)设需要增加m名业务员.
根据题意,得06(m+21)≥12.1×(1+10%)
解得m≥
∵m为正整数,m的最小值为2.
答:至少需要增加2名业务员.
26.
证明:因为EF⊥AE,所以∠AEF=90°,因为∠ABC=90°,所以∠ABF+∠AEF=180°,所以∠BAE+∠BFE=180°,因为∠BFE+∠EFC=180°,所以∠BAE=∠EFC,因为AB=BC,∠ABE=∠EBC=45°,BE=BE,所以△ABE≌△CBE,所以∠BAE=∠BCE,所以∠EFC=∠ECF,所以EF=EC。
BE=BF+ED
证明:过点E作EH⊥CD于点H,EK⊥BC于K,则四边形EHCK为矩形,所以EH=KC,因为EF=EC,所以FK=KC,因为
∠EDH=45°,∠EHD=90°,所以EH=DE,所以FK=DE,因为∠EBK=45°,EK⊥BK,所以BE=BK=(BF+FK)=(BF+DE)=BF+ED。
(3)解:过点C作CM⊥AC交FN于M,过点F作FQ⊥CM交CM延长线于Q,作FP⊥AC于点P,设∠DCE=α,则∠ECG=45°-α,∠CEF=2α,∠QCN=90°-∠ECG=45°+α,因为∠NFE=90°,所以∠N=90°-∠FEN=90°-2α,∠CMN=180°-∠N-∠NCM=45°+α,所以∠NMC=∠NCM,所以MN=NC=2.因为∠PCF=∠FCQ=45°,所以FQ=FP。因为∠GFP+∠PFM=∠QFM+∠PFM=90°,所以∠GFP=∠QEM,因为∠FPG=∠FQM=90°,所以△GFP≌△MFQ,所以设FG=FM=x,则EC=EF=x+1,EN=x+3,FN=x+2,在Rt△EFN中,,即,解得:x=2,所以FN=4.
27.解:(1)∵A(4,0)
AB∥OC,设点B的坐标为(4,y)(1分)?
∴把x=4代入y=-x+3中
得y=2
∴B(4,2)(2分)?
(2)过C点作CN⊥AB于N,∵AB∥OC,∴∠OCD=∠DMC
由题意∠DCM=∠OCM
∴∠DCM=∠DMC
∴CD=MD=5(1分)
∵y=-x+3
当x=0时
y=3
∴OC=3
∵CN=OA=4
∴NM=2(1分)
∴AM=1
∴M(4,1)(1分)
设l解析式y=kx+b
把(0,3)(4,1)代入
∴
∴l的解析式为:y=-x+3(1分)
(3)∵AD=6
BC为一边
∴D(4,6)
∴OD的解析式为:y=x
过P,Q作x轴平行线,设P(x,-x+3)
∴Q(x-4,4-x)代入y=x中
得x=5
∴P1(5,
)(1分)
同理P2(-2,4)(1分)
当BC为对角线时,设P(a,-a+3)
Q(b,
b)
∴P3(2,2)(1分)?
一、选择题(每小题3分,共计30分)
1.下列方程是一元二次方程的是(
)
A.x+2y=l
B.x+5=0
C.x+=8
D.3x+8=6x+2
2.正比例函数y=kx的图象经过点(1,2),则k的值为(
)
A.
-
B.
-2
C.
D.2
3.下列四条四组线段中,可以构成直角三角形的是(
)
A.
1,4,9
B.
5,6,7
C.5,12,13
D.
5,11,l2
4.一元二次方程x+x-4=0的根的情况是(
)
A.有两个相等的实数根
B.有两个不相等的实数根
C.没有实数根
D.只有一个实数根
5.一条长64厘米的铁丝被剪成两段,每段均折成正方形,且两个正方形的面积之差为160cm,若设较小的正方形的边长为xcm,则可列方程(
)
A.(16-x)-x=160
B.(64-x)-x=160
C.
x-(16-x)=160
D.(64-x)-x=160
6.对于函数y=-3x+1,下列结论结论正确的是(
)
A.它的图像必经过点(-l,3)
B.它的图经过第一、二、三象限
C.当x>时,y
7.如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使A的对应点A'落在对角线BD上,折痕为DG,则AG的长为
(
)
A.
1
B.
C.
D.
2
8.下列命题中,真命题的是(
)
A.一组对边平行,一组对角相等的四边形是平行四边形
B.两条对角线相等的四边形是矩形
C.一条对角线平分一组对角的四边形是菱形
D.四条边相等的四边形是正方形
9.菱形的周长为16厘米,两相邻角度数比是1:2,菱形的面积是(
)平方厘米
A.8
B.8
C.16
D.16
10.甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲、乙两人相距s(米),甲行走的时间为t(分)s关于t的函数图像的一部分如图所示,下列四种说法中:①甲行走的速度为30米/分;②乙出发l2.5分钟时追上甲;③当t=35时,a=450;④甲行走30.5分或38分时.甲、乙两人相距360米.其中正确的个数有(
).
A.11个
B.24个
C.3个
D.4个
二、填空题(每小题3分,共计30分)
11.函数y=中,自变量x的取值范围是
.
12.命题“如果两个实数相等,那么它们的平方相等”的逆命题是
.(填“真命题”或“假命题”)
13.已知m是是方程x-x-=0的一个根,则
m-m的值是
.
14.在Rt△ABC中,斜边AB=2,则
AB+BC+AC=
.
15.如图,在△ABC中,D、E分别是AB、AC的中点,若BC=10.则DE=
.
16.公司4月份利润为160万元.要使6月份的利润达到250万元,则平均每月增长的百分率是
.
17.如图,直线∥,平行四边形ABCD的面积为8,点E是直线上任意一点,连接BE、CE,则△EBC三角形的面积是
.
18.三角形的边长分别为3和5,要使这个三角形是直角三角形,则第三边长是
.
19.如图,函数y=-2x和y=kx+b图象相交于点A(m,3),关于x的不等式kx+b+2x>0的解集为
.
20.如图,四边形ABCD中,∠BAD=105°,∠ADC=120°,E是AD的中点,BE⊥EC,若AB=3,CD=,则BC=_________
三、解答题(共计60分)
21.解方程:
(1)
(2)
22.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画出以AB为对角线的正方形AEBF,点E、F在小正方形的顶点上;
(2)在方格纸中画出以CD为一边的菱形CDMN,点M、N在小正方形的顶点上,且菱形面积为8;
(3)在(1)、(2)的条件下,连接EN、EF、NF,请直接写出△EFN的面积.
23.如图,在平面直角坐标系中,直线与直线交于点A,两条直线分别与x轴交于点B,与y轴交于C.
(1)求点A的坐标;
(2)点D是AC上一点,BD=CD,求ΔBCD的面积.
24.四边形ABCD的对角线AC和BD相交于点O,AB=BC,AD=CD,过C作BD的平行线与过D作AC的平行线相交于点E.
(1)如图1,求证:四边形ODEC是矩形;
(2)如图2,连接OE,当AD∥BC时,在不添加任何辅助线及字母的情况下,请直接写出图中所有的平行四边形.
25.现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,哈市某家小型“大学生自主创业”的快递公司,今年1月份与3月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每位快递投递业务员每月最多可投递0.6万件,那么该公司现有21名快递投递业务员,若要完成今年4月份的快递投递任务,则至少需要增加几名业务员?
26.如图1,在正方形ABCD中,E在对角线BD上,过点E作
EF⊥AE,EF交BC于点F.
(1)求证:EF=CE;
(2)如图2,试判断BE、DE、BF的数量关系,并证明你的结论;
(3)如图3,连接AC交EF于点G,过点F作FN⊥EF交EC的延长线于点N,若EG=1,CN=2,求FN的长.
27.在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4,0),直线y=-x+3经过顶
点B,与y轴交于顶点C,AB∥OC.
(1)如图1,求顶点B的坐标;
(2)如图2,直线l经过点C,与直线AB交于点M,点O′为点O关于直线l的对称点,连接CO′,并延长交直线AB于第一象限的点D,当CD=5时,求直线l的解析式;
(3)在(2)的条件下,点P在直线l上运动,点Q在直线OD上运动,以P、Q、B、C为顶点的四边形能否成为平行四边形?若能,求出点P的坐标;若不能,说明理由.
综合复习题(三)
选择题
A
2.
D
3.
C
4.
B
5.
A
6.
C
7.
C
8.
A
9.B
10.C
二、填空题
11.x≠-4
12.
假命题
13.
14.
8
15.
5
16.25%
17.
4
18.
4或
19.x<
20.
三、解答题
21.,
,
22.
答案:(1)如图
(2)如图
(3)如图,=4.
23.解:(1)联立方程
解得:
∴点A的坐标为(,)
直线y=x+1令y=0,x=-1,∴B(-1,0)
直线y=-x+3
令y=0,x=4
∴C(4,0)
过点D作DE⊥x轴于点E
∵DB=DC
∴BE=CE=BC=
易得E(,0)
将x=代入中
y=
∴D(,)
SΔBCD=BC?DE=×5×=
24.(1)证明:∵CE∥BD,DE∥AC
∴四边形ODEC是平行四边形
∵AB=BC,AD=CD,BD=BD
∴△ABD≌△CBD
∴∠ABD=∠CBO
∵AB=BC
∴∠BAO=∠BCO
∴∠AOB=∠BOC.
∵∠AOB+∠BOC=180°,
∴∠AOB=∠BOC=90°
∴∠COD=90°
∴四边形ODEC是矩形
(2)□ABCD,□ODEC,□OBCE,□ADEO
25.解:(1)设该快递公司投递总件数的月平均增长车为x.
根据题意,得10(1+x)2=12.1,
解得:x1=0.1,x2=-2.1(舍去)
答:该快递公司授递总件数的月平均增长率为10%.
(2)设需要增加m名业务员.
根据题意,得06(m+21)≥12.1×(1+10%)
解得m≥
∵m为正整数,m的最小值为2.
答:至少需要增加2名业务员.
26.
证明:因为EF⊥AE,所以∠AEF=90°,因为∠ABC=90°,所以∠ABF+∠AEF=180°,所以∠BAE+∠BFE=180°,因为∠BFE+∠EFC=180°,所以∠BAE=∠EFC,因为AB=BC,∠ABE=∠EBC=45°,BE=BE,所以△ABE≌△CBE,所以∠BAE=∠BCE,所以∠EFC=∠ECF,所以EF=EC。
BE=BF+ED
证明:过点E作EH⊥CD于点H,EK⊥BC于K,则四边形EHCK为矩形,所以EH=KC,因为EF=EC,所以FK=KC,因为
∠EDH=45°,∠EHD=90°,所以EH=DE,所以FK=DE,因为∠EBK=45°,EK⊥BK,所以BE=BK=(BF+FK)=(BF+DE)=BF+ED。
(3)解:过点C作CM⊥AC交FN于M,过点F作FQ⊥CM交CM延长线于Q,作FP⊥AC于点P,设∠DCE=α,则∠ECG=45°-α,∠CEF=2α,∠QCN=90°-∠ECG=45°+α,因为∠NFE=90°,所以∠N=90°-∠FEN=90°-2α,∠CMN=180°-∠N-∠NCM=45°+α,所以∠NMC=∠NCM,所以MN=NC=2.因为∠PCF=∠FCQ=45°,所以FQ=FP。因为∠GFP+∠PFM=∠QFM+∠PFM=90°,所以∠GFP=∠QEM,因为∠FPG=∠FQM=90°,所以△GFP≌△MFQ,所以设FG=FM=x,则EC=EF=x+1,EN=x+3,FN=x+2,在Rt△EFN中,,即,解得:x=2,所以FN=4.
27.解:(1)∵A(4,0)
AB∥OC,设点B的坐标为(4,y)(1分)?
∴把x=4代入y=-x+3中
得y=2
∴B(4,2)(2分)?
(2)过C点作CN⊥AB于N,∵AB∥OC,∴∠OCD=∠DMC
由题意∠DCM=∠OCM
∴∠DCM=∠DMC
∴CD=MD=5(1分)
∵y=-x+3
当x=0时
y=3
∴OC=3
∵CN=OA=4
∴NM=2(1分)
∴AM=1
∴M(4,1)(1分)
设l解析式y=kx+b
把(0,3)(4,1)代入
∴
∴l的解析式为:y=-x+3(1分)
(3)∵AD=6
BC为一边
∴D(4,6)
∴OD的解析式为:y=x
过P,Q作x轴平行线,设P(x,-x+3)
∴Q(x-4,4-x)代入y=x中
得x=5
∴P1(5,
)(1分)
同理P2(-2,4)(1分)
当BC为对角线时,设P(a,-a+3)
Q(b,
b)
∴P3(2,2)(1分)?
同课章节目录
