全等三角形的判定SAS
图片预览


文档简介
(共13张PPT)
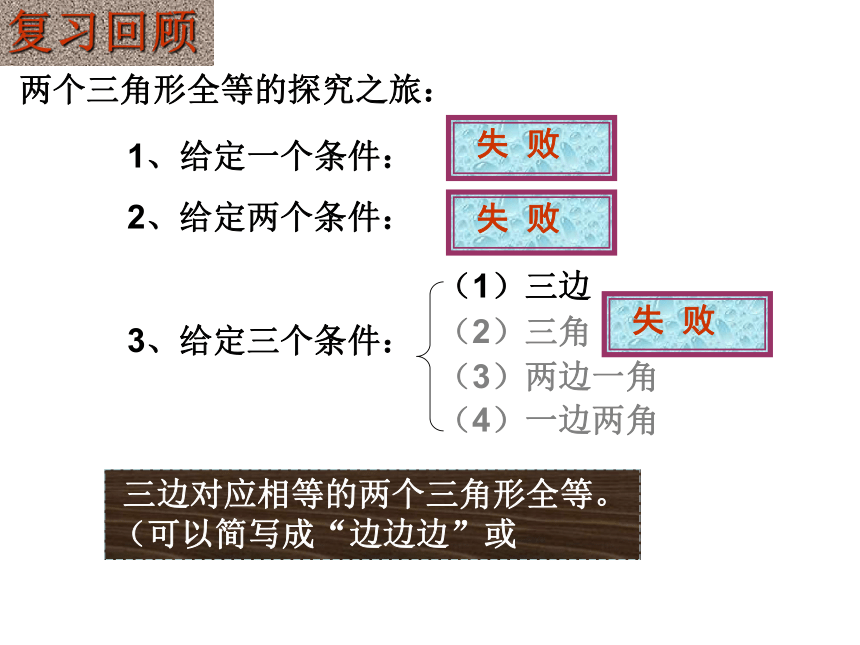
复习回顾
两个三角形全等的探究之旅:
1、给定一个条件:
2、给定两个条件:
失 败
失 败
3、给定三个条件:
(1)三边
(2)三角
(3)两边一角
三边对应相等的两个三角形全等。(可以简写成“边边边”或“SSS”)
(4)一边两角
失 败
探究三
给定三个条件:
(1)三边
(3)两边一角
(4)一边两角
(2)三角
两边及其夹角
两边及一边对角
1、两边及其夹角:
先任意画一个△ABC,再画一个△A’B’C’
使得A’B’=AB,A’C’=AC ,∠A’=∠A
观察所得的两个三角形是否全等。
[动手画一画]
2、两边及一边对角:
先任意画一个△ABC,再画一个△A’B’C’
使得A’B’=AB,A’C’=AC ,∠B’=∠B
观察所得的两个三角形是否全等。
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
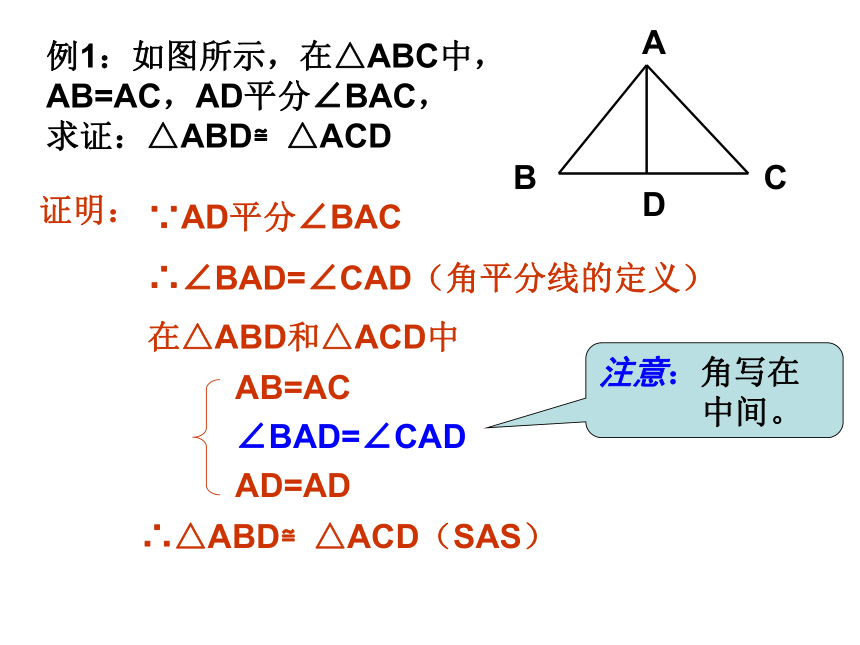
例1:如图所示,在△ABC中,AB=AC,AD平分∠BAC,
求证:△ABD≌△ACD
A
B
C
D
证明:
∵AD平分∠BAC
∴∠BAD=∠CAD(角平分线的定义)
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴△ABD≌△ACD(SAS)
注意:角写在
中间。
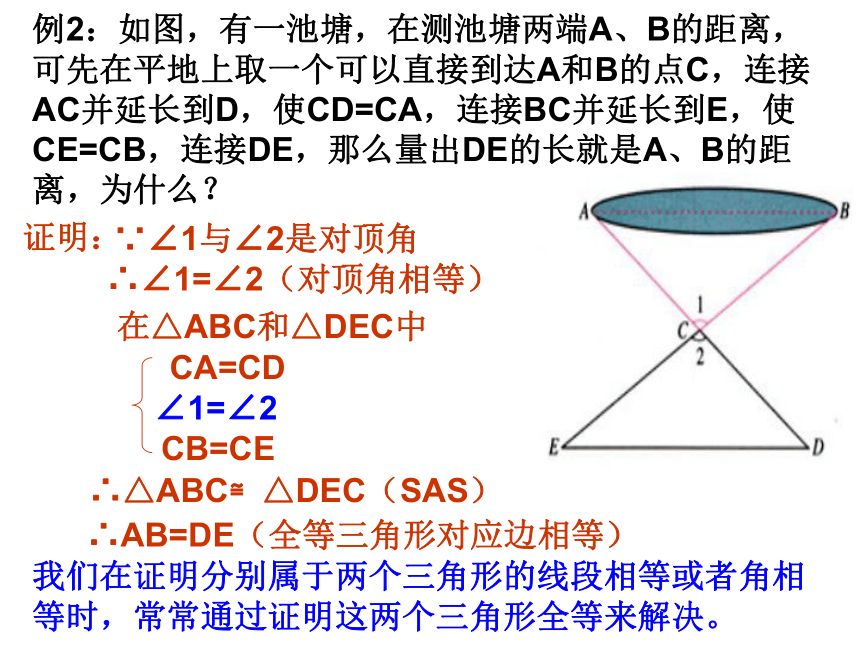
例2:如图,有一池塘,在测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长就是A、B的距离,为什么?
证明:
∵∠1与∠2是对顶角
∴∠1=∠2(对顶角相等)
在△ABC和△DEC中
CA=CD
∠1=∠2
CB=CE
∴△ABC≌△DEC(SAS)
∴AB=DE(全等三角形对应边相等)
我们在证明分别属于两个三角形的线段相等或者角相等时,常常通过证明这两个三角形全等来解决。
C
A
B
D
O
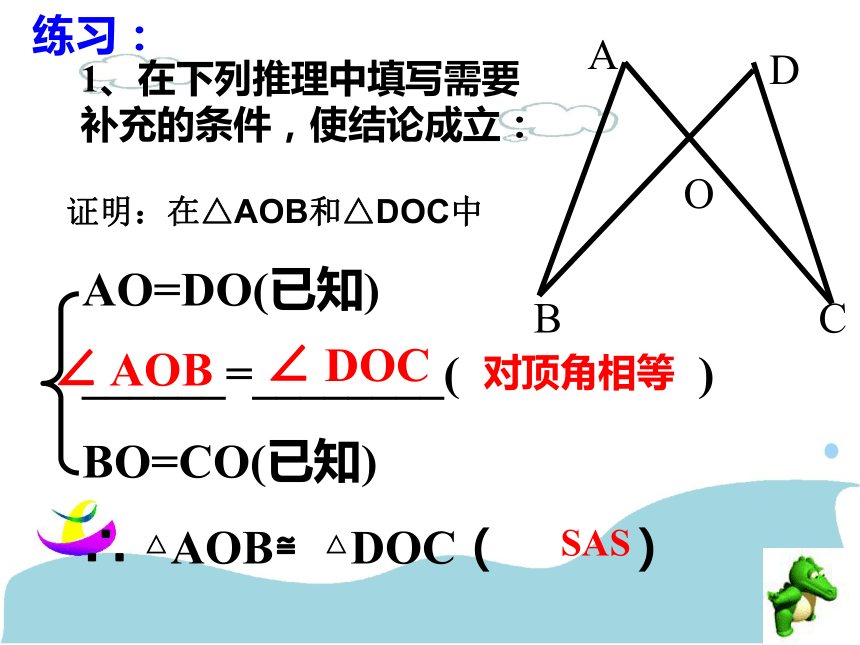
1、在下列推理中填写需要补充的条件,使结论成立:
AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )
∠ AOB
∠ DOC
对顶角相等
SAS
练习:
证明:在△AOB和△DOC中
2、如图,在△AEC和△ADB中,已知AE=AD,AC=AB请说明△AEC ≌ △ADB的理由。
____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )
A
E
B
D
C
AE
AD
AC
AB
SAS
解:在△AEC和△ADB中
练一练
3、如图,两车从路段AB的一端A出发,分别向东,向西行进相同的距离,到达C、D两地,此时C、D到B的距离相等吗?为什么?
4、如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,求证:∠A=∠D
经过本节课的学习,你有哪些收获?
例3:如图,已知AE=CF,AD∥BC,AD=CB,
求证:△ADF≌ △CBE
A
D
B
C
E
F
证明:
∵AD∥BC
∴∠A=∠C
∵AE=CF
即AF+FE=CE+EF
∴AF=CE
在△ADF和△CBE中
AD=CB
∠A=∠C
AF=CE
∴△ADF≌ △CBE(SAS)
变式一:如图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,DE=BF,AE=CF,求证:AB∥CD
A
B
C
E
D
F
证明:
∵AE=CF
即AF+FE=CE+EF
∴AF=CE
∵ DE⊥AC,BF⊥AC
∴∠DEC=∠BFA=90
在△DEC与△BFA中
DE=BF
CE=AF
∠DEC=∠BFA
∴ △DEC≌ △BFA(SAS)
∴∠DCE=∠BAF(全等三角形对应角相等)
∴ AB∥CD(内错角相等,两直线平行)
变式二:如图,已知EB⊥AD于B,FC⊥AD于C,且EB=FC,AB=CD,求证:AF=DE
A
B
C
D
E
F
证明:
∵AB=CD
∴AB+BC=CD+CB
即AC=DB
∵ EB⊥AD,FC⊥AD
∴∠FCA=∠EBD=90
在△AFC与△DEB中
AC=DB
FC=EB
∠FCA=∠EBD
∴ △ AFC≌ △DEB (SAS)
∴AF=DE(全等三角形对应边相等)
例4:如图所示,已知AB=DC,AC=DB,图中有哪些三角形全等?为什么?
A
B
C
D
O
1
2
△ABC≌ △DCB(SSS)
△ABO≌ △DCO(SAS)
例5:如图,AB=CB,AD=CD,E是BD上任意一点,
求证:AE=CE
A
B
D
C
E
改变E的位置你还会证明吗?
复习回顾
两个三角形全等的探究之旅:
1、给定一个条件:
2、给定两个条件:
失 败
失 败
3、给定三个条件:
(1)三边
(2)三角
(3)两边一角
三边对应相等的两个三角形全等。(可以简写成“边边边”或“SSS”)
(4)一边两角
失 败
探究三
给定三个条件:
(1)三边
(3)两边一角
(4)一边两角
(2)三角
两边及其夹角
两边及一边对角
1、两边及其夹角:
先任意画一个△ABC,再画一个△A’B’C’
使得A’B’=AB,A’C’=AC ,∠A’=∠A
观察所得的两个三角形是否全等。
[动手画一画]
2、两边及一边对角:
先任意画一个△ABC,再画一个△A’B’C’
使得A’B’=AB,A’C’=AC ,∠B’=∠B
观察所得的两个三角形是否全等。
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
例1:如图所示,在△ABC中,AB=AC,AD平分∠BAC,
求证:△ABD≌△ACD
A
B
C
D
证明:
∵AD平分∠BAC
∴∠BAD=∠CAD(角平分线的定义)
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴△ABD≌△ACD(SAS)
注意:角写在
中间。
例2:如图,有一池塘,在测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长就是A、B的距离,为什么?
证明:
∵∠1与∠2是对顶角
∴∠1=∠2(对顶角相等)
在△ABC和△DEC中
CA=CD
∠1=∠2
CB=CE
∴△ABC≌△DEC(SAS)
∴AB=DE(全等三角形对应边相等)
我们在证明分别属于两个三角形的线段相等或者角相等时,常常通过证明这两个三角形全等来解决。
C
A
B
D
O
1、在下列推理中填写需要补充的条件,使结论成立:
AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )
∠ AOB
∠ DOC
对顶角相等
SAS
练习:
证明:在△AOB和△DOC中
2、如图,在△AEC和△ADB中,已知AE=AD,AC=AB请说明△AEC ≌ △ADB的理由。
____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )
A
E
B
D
C
AE
AD
AC
AB
SAS
解:在△AEC和△ADB中
练一练
3、如图,两车从路段AB的一端A出发,分别向东,向西行进相同的距离,到达C、D两地,此时C、D到B的距离相等吗?为什么?
4、如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,求证:∠A=∠D
经过本节课的学习,你有哪些收获?
例3:如图,已知AE=CF,AD∥BC,AD=CB,
求证:△ADF≌ △CBE
A
D
B
C
E
F
证明:
∵AD∥BC
∴∠A=∠C
∵AE=CF
即AF+FE=CE+EF
∴AF=CE
在△ADF和△CBE中
AD=CB
∠A=∠C
AF=CE
∴△ADF≌ △CBE(SAS)
变式一:如图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,DE=BF,AE=CF,求证:AB∥CD
A
B
C
E
D
F
证明:
∵AE=CF
即AF+FE=CE+EF
∴AF=CE
∵ DE⊥AC,BF⊥AC
∴∠DEC=∠BFA=90
在△DEC与△BFA中
DE=BF
CE=AF
∠DEC=∠BFA
∴ △DEC≌ △BFA(SAS)
∴∠DCE=∠BAF(全等三角形对应角相等)
∴ AB∥CD(内错角相等,两直线平行)
变式二:如图,已知EB⊥AD于B,FC⊥AD于C,且EB=FC,AB=CD,求证:AF=DE
A
B
C
D
E
F
证明:
∵AB=CD
∴AB+BC=CD+CB
即AC=DB
∵ EB⊥AD,FC⊥AD
∴∠FCA=∠EBD=90
在△AFC与△DEB中
AC=DB
FC=EB
∠FCA=∠EBD
∴ △ AFC≌ △DEB (SAS)
∴AF=DE(全等三角形对应边相等)
例4:如图所示,已知AB=DC,AC=DB,图中有哪些三角形全等?为什么?
A
B
C
D
O
1
2
△ABC≌ △DCB(SSS)
△ABO≌ △DCO(SAS)
例5:如图,AB=CB,AD=CD,E是BD上任意一点,
求证:AE=CE
A
B
D
C
E
改变E的位置你还会证明吗?
