苏科版八年级上册数学 第5章《平面直角坐标系》单元检测 (Word版 含答案)
文档属性
| 名称 | 苏科版八年级上册数学 第5章《平面直角坐标系》单元检测 (Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 314.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-17 00:00:00 | ||
图片预览

文档简介
第5章《平面直角坐标系》单元检测
一、选择题
(每题2分,共16分)
1.以下是甲、乙、丙三人看地图时对四个坐标的描述:
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到邮局.
丙:邮局在火车站西200米处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站的是
(
)
A.向南直走300米,再向西直走200米
B.向南直走300米,再向西直走100米
C.向南直走700米,再向西直走200米
D.向南直走700米,再向西直走600米
2.在平面直角坐标系中,若点P的坐标为
(-3,2),则点P所在的象限是
(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.若点P
(a+1,2a-3)关于x轴的对称点在第一象限,则a的取值范围是
(
)
A.a<-1
B.-1C.-D.a>
4.如图,若象棋盘上建立直角坐标系,使“将”位于点
(1,-2),“象”位于点(3,-2),则“炮”位于点
(
)
A.(1,-1)
B.(-1,1)
C.(-1,2)
D:(1,-2)
5.定义:平面内的直线l1与l2相交于点O,若对于该
平面内任意一点M,点M到直线l1,l2的距离分别为a,b,则称有序非负实数对
(a,b)
是点M的“距离坐标”.根据上述定义,距离坐标为
(2,3)
的点的个数是
(
)
A.2
B.1
C.4
D.3
6.一辆汽车行驶的路程与行驶时间的关系如图所示,则下列说法正确的是
(
)
A.前3h中汽车的速度越来越快
B.3h后汽车静止不动
C.3
h后汽车以相同的速度行驶
D.前3
h汽车以相同的速度行驶
7.如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P的个数是
(
)
A.2
B.3
C.4
D.5
8.图中反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家.如果菜地和青稞地的距离为a
km,小刚在青稞地除草比在菜地浇水多用了b
min,那么a,b的值分别为
(
)
A.1,8
B.0.5,12
C.1,12
D.0.5,8
二、填空题
(每题2分,共20分)
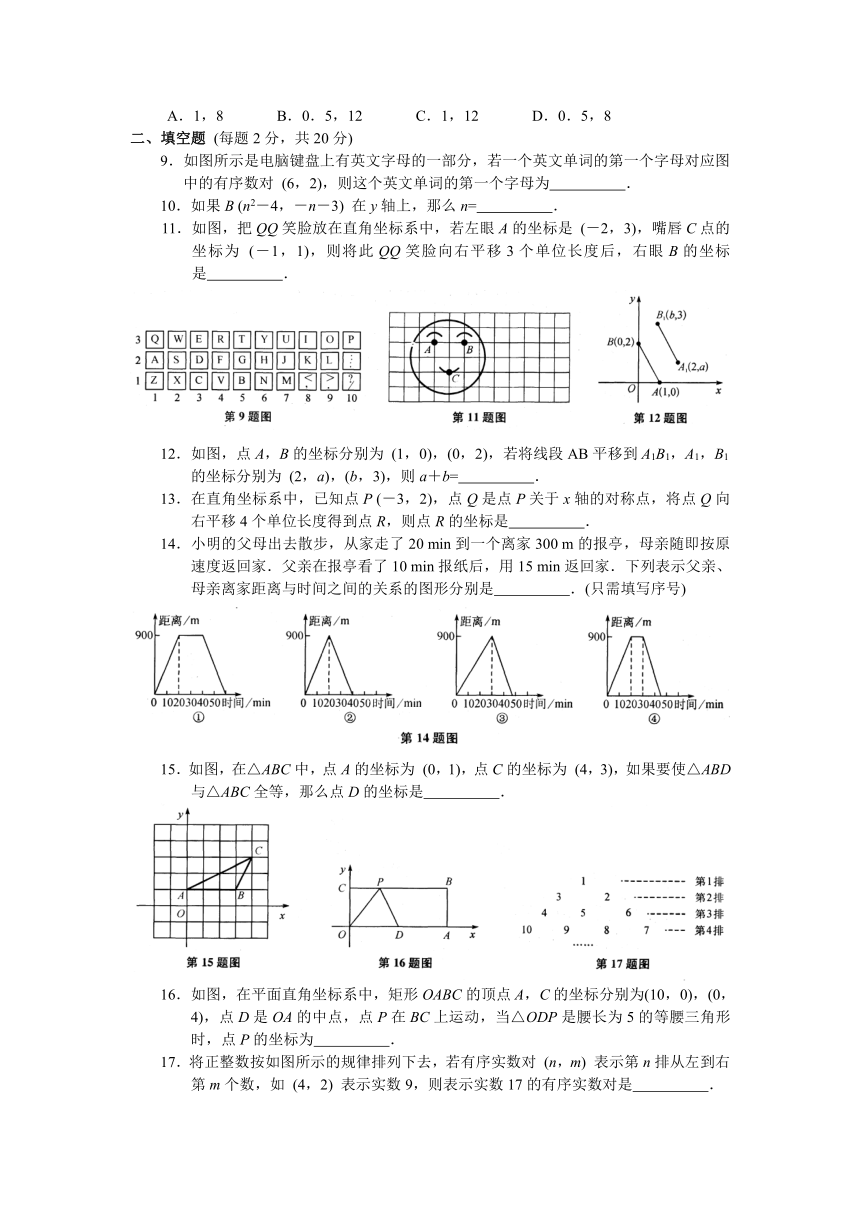
9.如图所示是电脑键盘上有英文字母的一部分,若一个英文单词的第一个字母对应图中的有序数对
(6,2),则这个英文单词的第一个字母为
.
10.如果B
(n2-4,-n-3)
在y轴上,那么n=
.
11.如图,把QQ笑脸放在直角坐标系中,若左眼A的坐标是
(-2,3),嘴唇C点的坐标为
(-1,1),则将此QQ笑脸向右平移3个单位长度后,右眼B的坐标是
.
12.如图,点A,B的坐标分别为
(1,0),(0,2),若将线段AB平移到A1B1,A1,B1的坐标分别为
(2,a),(b,3),则a+b=
.
13.在直角坐标系中,已知点P
(-3,2),点Q是点P关于x轴的对称点,将点Q向右平移4个单位长度得到点R,则点R的坐标是
.
14.小明的父母出去散步,从家走了20
min到一个离家300
m的报亭,母亲随即按原速度返回家.父亲在报亭看了10
min报纸后,用15
min返回家.下列表示父亲、母亲离家距离与时间之间的关系的图形分别是
.(只需填写序号)
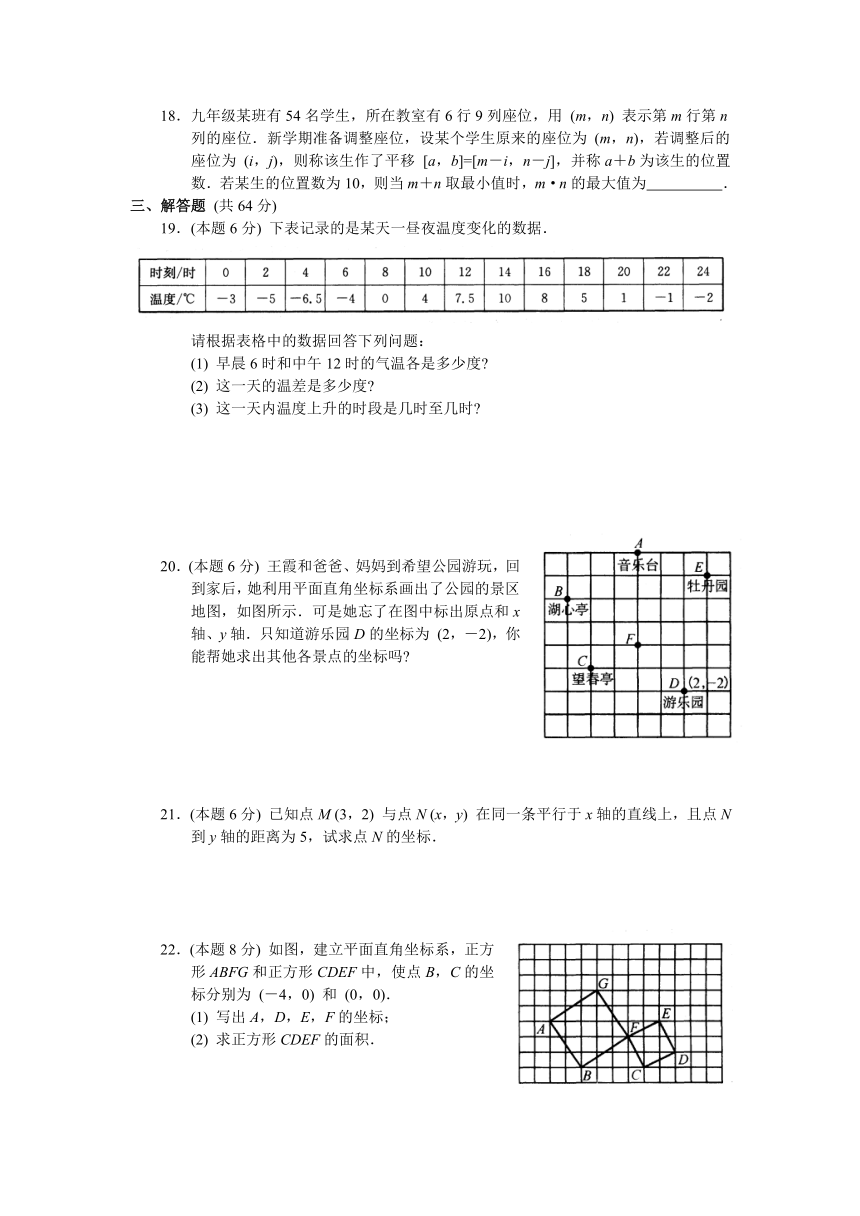
15.如图,在△ABC中,点A的坐标为
(0,1),点C的坐标为
(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是
.
16.如图,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为
.
17.将正整数按如图所示的规律排列下去,若有序实数对
(n,m)
表示第n排从左到右第m个数,如
(4,2)
表示实数9,则表示实数17的有序实数对是
.
18.九年级某班有54名学生,所在教室有6行9列座位,用
(m,n)
表示第m行第n列的座位.新学期准备调整座位,设某个学生原来的座位为
(m,n),若调整后的座位为
(i,j),则称该生作了平移
[a,b]=[m-i,n-j],并称a+b为该生的位置数.若某生的位置数为10,则当m+n取最小值时,m·n的最大值为
.
三、解答题
(共64分)
19.(本题6分)
下表记录的是某天一昼夜温度变化的数据.
请根据表格中的数据回答下列问题:
(1)
早晨6时和中午12时的气温各是多少度?
(2)
这一天的温差是多少度?
(3)
这一天内温度上升的时段是几时至几时?
20.(本题6分)
王霞和爸爸、妈妈到希望公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为
(2,-2),你能帮她求出其他各景点的坐标吗?
21.(本题6分)
已知点M
(3,2)
与点N
(x,y)
在同一条平行于x轴的直线上,且点N到y轴的距离为5,试求点N的坐标.
22.(本题8分)
如图,建立平面直角坐标系,正方形ABFG和正方形CDEF中,使点B,C的坐标分别为
(-4,0)
和
(0,0).
(1)
写出A,D,E,F的坐标;
(2)
求正方形CDEF的面积.
23.(本题9分)
如图所示为一风筝的图案.
(1)
写出图中所标各个顶点的坐标.
(2)
若图中各点的纵坐标保持不变,横坐标
分别乘以2,所得各点的坐标分别是什么?所得图案与原来图案相比有什么变化?
(3)
若图中各点的横坐标保持不变,纵坐标
分别乘以-2,所得各点的坐标分别是什么?
所得图案与原来(1)中的图案相比有什么变化?
24.(本题8分)
如图,四边形OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.
25.(本题10分)
操作与探究.
(1)
对数轴上的点P进行如下操作:先把点P表示的数乘以,再把所得数对应的点向右平移1个单位长度,得到点P的对应点P′.
点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是-3,则点A′表示的数是
;若点B′表示的数是2,则点B表示的数是
;已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是
.
(2)
如图2,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:
把每个点的横、纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度
(m>0,n>0),得到正方形A'B'C'D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
26.(本题10分)【操作发现】在计算器上输入一个正数,不断地按“”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1,先在直线y=kx+b上确定点(x1,y1),再在直线y=x上确定纵坐标为y1的点(x2,y1),然后再x轴上确定对应的数x2,…,以此类推.
【解决问题】研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
(1)若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;
(2)若k>1,又得到什么结论?请说明理由;
(3)①若k=﹣,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示)
参考答案
一、选择题
1.A
2.B
3.B
4.B
5.C
6.B
7.C
(提示:满足条件的点P在x轴正半轴上有3个,在x轴负半轴上有1个)
8.D
[提示:由图形可得a=1.5-1=0.5,b=(56-33)-(27-12)=8]
二、填空题
9.H
10.±2
11.(3,3)
12.2
13.(1,-2)
14.④、②
15.(-1,3)
或
(4,-1)
或
(-1,-1)
16.(2,4)
或
(3,4)
或
(8,4)
17.(6,5)
18.36
[提示:由已知,得a+b=m-i+n-j,即m-i+n-j=10,∴
m+n=10+i+j.当m+n取最小值时,i+j的最小值为2,∴
m+n的最小值为12.即n=12-m,m·n=m(12-m)=
-(m-6)2+36,∴
当m=6时,m·n有最大值为6×6=36]
三、解答题
19.(1)
-4℃,7.5℃
(2)
16.5℃
(3)
4时~14时
20.由题意可知,本题是以点F为坐标原点(0,0),FA为y轴的正半轴,建立平面直角坐标系,则A,B,C,E的坐标分别为:A
(0,4),B
(-3,2),C
(-2,-1),E
(3,3)
21.(-5,2),(5,2)
22.(1)
建立直角坐标系如图所示,A
(-6,3),D
(2,1),E
(1,
3),F
(-1,2)
(2)
∵
CD2=22+12=5,∴
正方形CDEF的面积等于5
23.(1)
A
(0,4),B
(-3,1),C
(-3,-1),D
(0,-2),E
(3,
-1),F
(3,1)
(2)
所得各点的坐标分别为A
(0,4),B
(-6,1),C
(-6,-1),D
(0,-2),E
(6,-1),F
(6,1).与原图案相比,新图案在x轴方向上扩大到原来的2倍,在y轴方向上不变
(3)
所得各点的坐标分别为A
(0,-8),B
(-3,-2),C
(-3,2),D
(0,4),E
(3,2),F
(3,-2).与原图案相比,新图案在y轴方向上扩大到原来的2倍,方向相反,在x轴方向上不变
24.(1)
由题意可知折痕AD是四边形OAED的对称轴.在Rt△ABE中,AE=AO=10,AB=8,BE===6,∴
CE=4,∴
E(4,8).在Rt△DCE中,DC2+CE2=DE2.又DE=OD,∴
(8-OD)2+42=OD2,∴
OD=5,∴
D(0,5)
25.(1)
0
3
(2)
设点F的坐标为
(x,y),由题意得
解得
n=2.又∵
正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,∴
解得
∴
F(1,4)
26.
(1)若k=2,b=﹣4,y=2x﹣4,
取x1=3,则x2=2,x3=0,x4=﹣4,…
取x1=4,则x2x3=x4=4,…
取x1=5,则x2=6,x3=8,x4=12,…由此发现:
当x1<4时,随着运算次数n的增加,运算结果xn越来越小.
当x1=4时,随着运算次数n的增加,运算结果xn的值保持不变,都等于4.
当x1>4时,随着运算次数n的增加,运算结果xn越来越大.
(2)当x1>时,随着运算次数n的增加,xn越来越大.
当x1<时,随着运算次数n的增加,xn越来越小.
当x1=时,随着运算次数n的增加,xn保持不变.
理由:如图1中,直线y=kx+b与直线y=x的交点坐标为(,),
当x1>时,对于同一个x的值,kx+b>x,
∴y1>x1
∵y1=x2,
∴x1<x2,同理x2<x3<…<xn,
∴当x1>时,随着运算次数n的增加,xn越来越大.
同理,当x1<时,随着运算次数n的增加,xn越来越小.
当x1=时,随着运算次数n的增加,xn保持不变.
(3)①在数轴上表示的x1,x2,x3如图2所示.
随着运算次数的增加,运算结果越来越接近.
②由(2)可知:﹣1<k<1且k≠0,
由消去y得到x=
∴由①探究可知:m=.
一、选择题
(每题2分,共16分)
1.以下是甲、乙、丙三人看地图时对四个坐标的描述:
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到邮局.
丙:邮局在火车站西200米处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站的是
(
)
A.向南直走300米,再向西直走200米
B.向南直走300米,再向西直走100米
C.向南直走700米,再向西直走200米
D.向南直走700米,再向西直走600米
2.在平面直角坐标系中,若点P的坐标为
(-3,2),则点P所在的象限是
(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.若点P
(a+1,2a-3)关于x轴的对称点在第一象限,则a的取值范围是
(
)
A.a<-1
B.-1
4.如图,若象棋盘上建立直角坐标系,使“将”位于点
(1,-2),“象”位于点(3,-2),则“炮”位于点
(
)
A.(1,-1)
B.(-1,1)
C.(-1,2)
D:(1,-2)
5.定义:平面内的直线l1与l2相交于点O,若对于该
平面内任意一点M,点M到直线l1,l2的距离分别为a,b,则称有序非负实数对
(a,b)
是点M的“距离坐标”.根据上述定义,距离坐标为
(2,3)
的点的个数是
(
)
A.2
B.1
C.4
D.3
6.一辆汽车行驶的路程与行驶时间的关系如图所示,则下列说法正确的是
(
)
A.前3h中汽车的速度越来越快
B.3h后汽车静止不动
C.3
h后汽车以相同的速度行驶
D.前3
h汽车以相同的速度行驶
7.如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P的个数是
(
)
A.2
B.3
C.4
D.5
8.图中反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家.如果菜地和青稞地的距离为a
km,小刚在青稞地除草比在菜地浇水多用了b
min,那么a,b的值分别为
(
)
A.1,8
B.0.5,12
C.1,12
D.0.5,8
二、填空题
(每题2分,共20分)
9.如图所示是电脑键盘上有英文字母的一部分,若一个英文单词的第一个字母对应图中的有序数对
(6,2),则这个英文单词的第一个字母为
.
10.如果B
(n2-4,-n-3)
在y轴上,那么n=
.
11.如图,把QQ笑脸放在直角坐标系中,若左眼A的坐标是
(-2,3),嘴唇C点的坐标为
(-1,1),则将此QQ笑脸向右平移3个单位长度后,右眼B的坐标是
.
12.如图,点A,B的坐标分别为
(1,0),(0,2),若将线段AB平移到A1B1,A1,B1的坐标分别为
(2,a),(b,3),则a+b=
.
13.在直角坐标系中,已知点P
(-3,2),点Q是点P关于x轴的对称点,将点Q向右平移4个单位长度得到点R,则点R的坐标是
.
14.小明的父母出去散步,从家走了20
min到一个离家300
m的报亭,母亲随即按原速度返回家.父亲在报亭看了10
min报纸后,用15
min返回家.下列表示父亲、母亲离家距离与时间之间的关系的图形分别是
.(只需填写序号)
15.如图,在△ABC中,点A的坐标为
(0,1),点C的坐标为
(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是
.
16.如图,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为
.
17.将正整数按如图所示的规律排列下去,若有序实数对
(n,m)
表示第n排从左到右第m个数,如
(4,2)
表示实数9,则表示实数17的有序实数对是
.
18.九年级某班有54名学生,所在教室有6行9列座位,用
(m,n)
表示第m行第n列的座位.新学期准备调整座位,设某个学生原来的座位为
(m,n),若调整后的座位为
(i,j),则称该生作了平移
[a,b]=[m-i,n-j],并称a+b为该生的位置数.若某生的位置数为10,则当m+n取最小值时,m·n的最大值为
.
三、解答题
(共64分)
19.(本题6分)
下表记录的是某天一昼夜温度变化的数据.
请根据表格中的数据回答下列问题:
(1)
早晨6时和中午12时的气温各是多少度?
(2)
这一天的温差是多少度?
(3)
这一天内温度上升的时段是几时至几时?
20.(本题6分)
王霞和爸爸、妈妈到希望公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为
(2,-2),你能帮她求出其他各景点的坐标吗?
21.(本题6分)
已知点M
(3,2)
与点N
(x,y)
在同一条平行于x轴的直线上,且点N到y轴的距离为5,试求点N的坐标.
22.(本题8分)
如图,建立平面直角坐标系,正方形ABFG和正方形CDEF中,使点B,C的坐标分别为
(-4,0)
和
(0,0).
(1)
写出A,D,E,F的坐标;
(2)
求正方形CDEF的面积.
23.(本题9分)
如图所示为一风筝的图案.
(1)
写出图中所标各个顶点的坐标.
(2)
若图中各点的纵坐标保持不变,横坐标
分别乘以2,所得各点的坐标分别是什么?所得图案与原来图案相比有什么变化?
(3)
若图中各点的横坐标保持不变,纵坐标
分别乘以-2,所得各点的坐标分别是什么?
所得图案与原来(1)中的图案相比有什么变化?
24.(本题8分)
如图,四边形OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.
25.(本题10分)
操作与探究.
(1)
对数轴上的点P进行如下操作:先把点P表示的数乘以,再把所得数对应的点向右平移1个单位长度,得到点P的对应点P′.
点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是-3,则点A′表示的数是
;若点B′表示的数是2,则点B表示的数是
;已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是
.
(2)
如图2,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:
把每个点的横、纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度
(m>0,n>0),得到正方形A'B'C'D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
26.(本题10分)【操作发现】在计算器上输入一个正数,不断地按“”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1,先在直线y=kx+b上确定点(x1,y1),再在直线y=x上确定纵坐标为y1的点(x2,y1),然后再x轴上确定对应的数x2,…,以此类推.
【解决问题】研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
(1)若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;
(2)若k>1,又得到什么结论?请说明理由;
(3)①若k=﹣,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示)
参考答案
一、选择题
1.A
2.B
3.B
4.B
5.C
6.B
7.C
(提示:满足条件的点P在x轴正半轴上有3个,在x轴负半轴上有1个)
8.D
[提示:由图形可得a=1.5-1=0.5,b=(56-33)-(27-12)=8]
二、填空题
9.H
10.±2
11.(3,3)
12.2
13.(1,-2)
14.④、②
15.(-1,3)
或
(4,-1)
或
(-1,-1)
16.(2,4)
或
(3,4)
或
(8,4)
17.(6,5)
18.36
[提示:由已知,得a+b=m-i+n-j,即m-i+n-j=10,∴
m+n=10+i+j.当m+n取最小值时,i+j的最小值为2,∴
m+n的最小值为12.即n=12-m,m·n=m(12-m)=
-(m-6)2+36,∴
当m=6时,m·n有最大值为6×6=36]
三、解答题
19.(1)
-4℃,7.5℃
(2)
16.5℃
(3)
4时~14时
20.由题意可知,本题是以点F为坐标原点(0,0),FA为y轴的正半轴,建立平面直角坐标系,则A,B,C,E的坐标分别为:A
(0,4),B
(-3,2),C
(-2,-1),E
(3,3)
21.(-5,2),(5,2)
22.(1)
建立直角坐标系如图所示,A
(-6,3),D
(2,1),E
(1,
3),F
(-1,2)
(2)
∵
CD2=22+12=5,∴
正方形CDEF的面积等于5
23.(1)
A
(0,4),B
(-3,1),C
(-3,-1),D
(0,-2),E
(3,
-1),F
(3,1)
(2)
所得各点的坐标分别为A
(0,4),B
(-6,1),C
(-6,-1),D
(0,-2),E
(6,-1),F
(6,1).与原图案相比,新图案在x轴方向上扩大到原来的2倍,在y轴方向上不变
(3)
所得各点的坐标分别为A
(0,-8),B
(-3,-2),C
(-3,2),D
(0,4),E
(3,2),F
(3,-2).与原图案相比,新图案在y轴方向上扩大到原来的2倍,方向相反,在x轴方向上不变
24.(1)
由题意可知折痕AD是四边形OAED的对称轴.在Rt△ABE中,AE=AO=10,AB=8,BE===6,∴
CE=4,∴
E(4,8).在Rt△DCE中,DC2+CE2=DE2.又DE=OD,∴
(8-OD)2+42=OD2,∴
OD=5,∴
D(0,5)
25.(1)
0
3
(2)
设点F的坐标为
(x,y),由题意得
解得
n=2.又∵
正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,∴
解得
∴
F(1,4)
26.
(1)若k=2,b=﹣4,y=2x﹣4,
取x1=3,则x2=2,x3=0,x4=﹣4,…
取x1=4,则x2x3=x4=4,…
取x1=5,则x2=6,x3=8,x4=12,…由此发现:
当x1<4时,随着运算次数n的增加,运算结果xn越来越小.
当x1=4时,随着运算次数n的增加,运算结果xn的值保持不变,都等于4.
当x1>4时,随着运算次数n的增加,运算结果xn越来越大.
(2)当x1>时,随着运算次数n的增加,xn越来越大.
当x1<时,随着运算次数n的增加,xn越来越小.
当x1=时,随着运算次数n的增加,xn保持不变.
理由:如图1中,直线y=kx+b与直线y=x的交点坐标为(,),
当x1>时,对于同一个x的值,kx+b>x,
∴y1>x1
∵y1=x2,
∴x1<x2,同理x2<x3<…<xn,
∴当x1>时,随着运算次数n的增加,xn越来越大.
同理,当x1<时,随着运算次数n的增加,xn越来越小.
当x1=时,随着运算次数n的增加,xn保持不变.
(3)①在数轴上表示的x1,x2,x3如图2所示.
随着运算次数的增加,运算结果越来越接近.
②由(2)可知:﹣1<k<1且k≠0,
由消去y得到x=
∴由①探究可知:m=.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
