人教版九年级数学上册 24.1.4 圆周角 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学上册 24.1.4 圆周角 同步练习(Word版 含答案) | 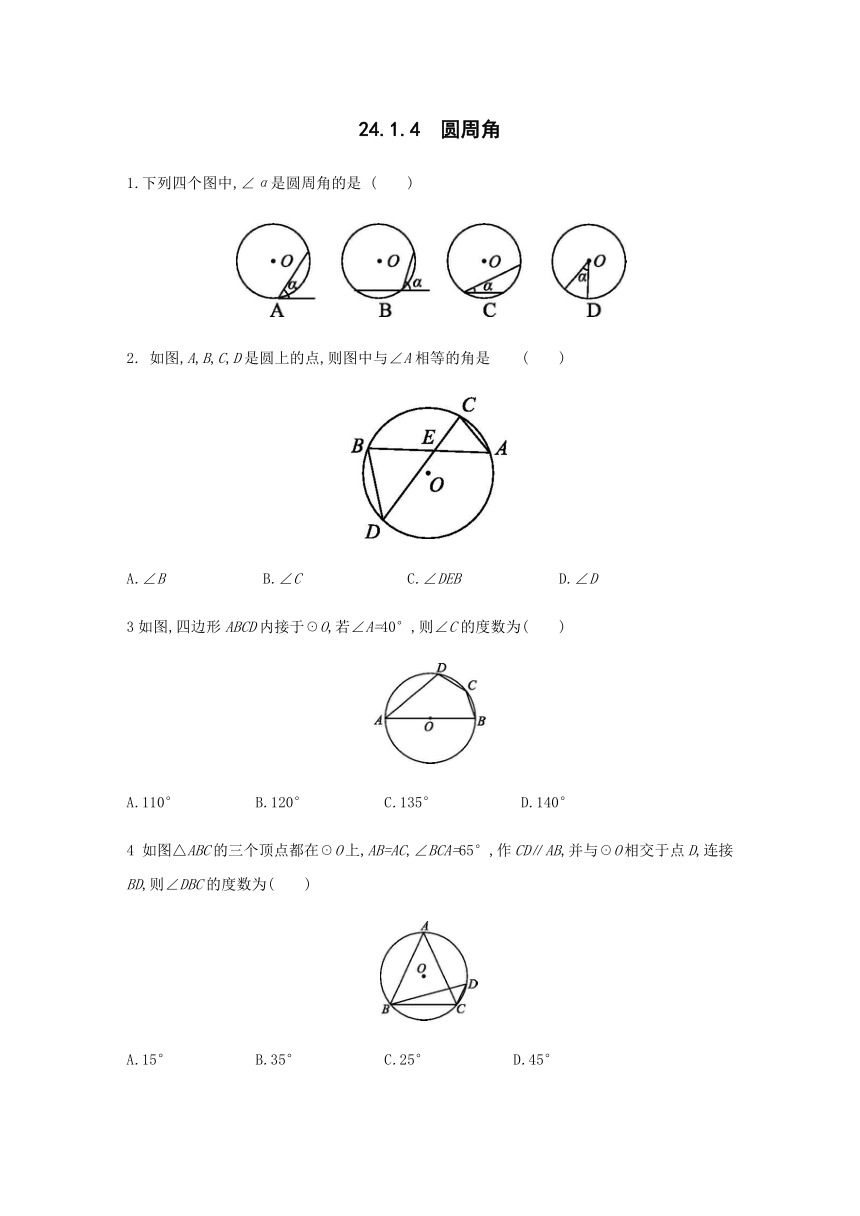 | |
| 格式 | zip | ||
| 文件大小 | 271.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-17 21:02:02 | ||
图片预览



文档简介
24.1.4 圆周角
1.下列四个图中,∠α是圆周角的是
( )
2.
如图,A,B,C,D是圆上的点,则图中与∠A相等的角是
( )
A.∠B
B.∠C
C.∠DEB
D.∠D
3如图,四边形ABCD内接于☉O,若∠A=40°,则∠C的度数为( )
A.110°
B.120°
C.135°
D.140°
4
如图△ABC的三个顶点都在☉O上,AB=AC,∠BCA=65°,作CD∥AB,并与☉O相交于点D,连接BD,则∠DBC的度数为( )
A.15°
B.35°
C.25°
D.45°
5.如图,点A,B,C在☉O上,∠AOB=72°,则∠ACB等于( )
A.28°
B.54°
C.18°
D.36°
6.如图所示,把一个量角器放置在△ABC的上面,根据量角器的读数可得∠BAC的度数是( )
A.60°
B.30°
C.20°
D.15°
7.如图,AB是☉O的直径,C,D是☉O上的两点,∠AOC=120°,则∠CDB= °.?
8.如图,在☉O中,半径OC⊥弦AB于点D,点E在☉O上,∠E=22.5°,AB=4,则半径OB= .?
9.如图已知AB是☉O的直径,点C在☉O上,若∠CAB=40°,则∠ABC= °.?
10
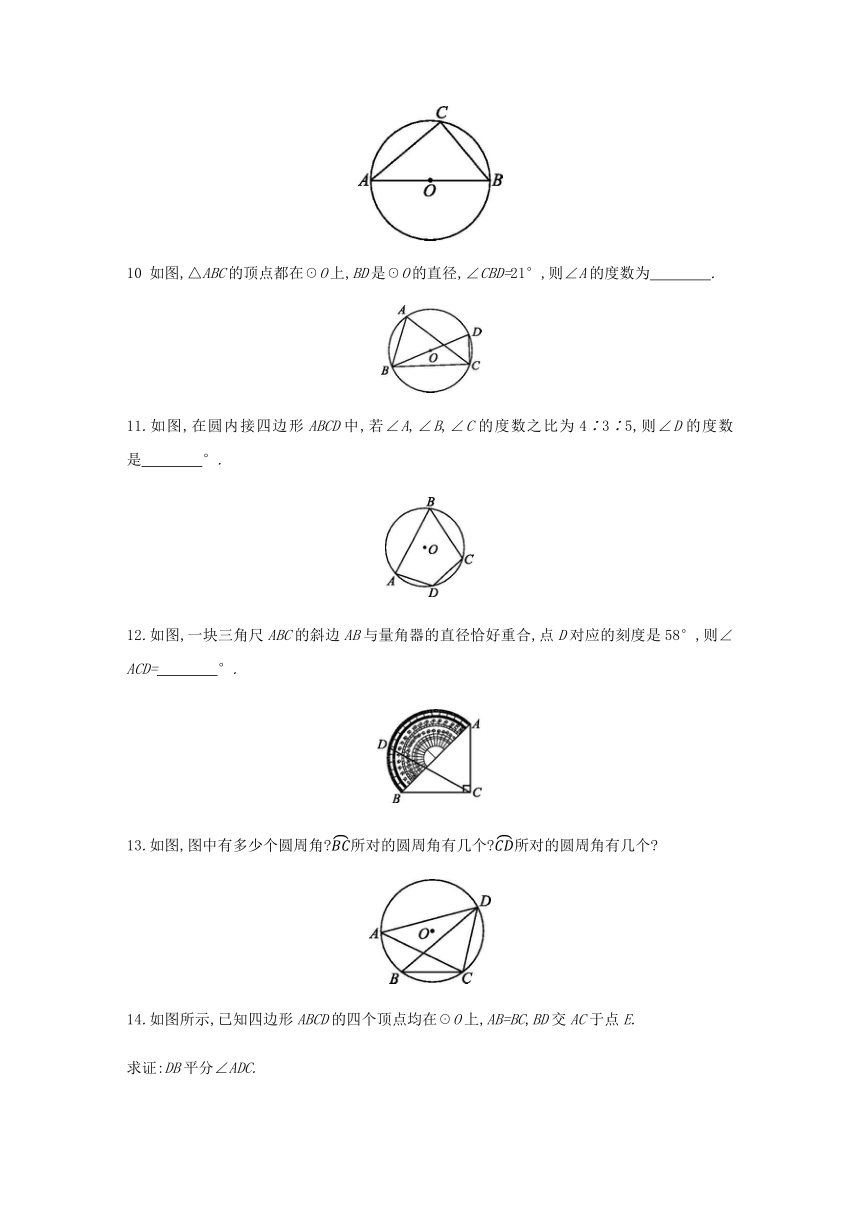
如图,△ABC的顶点都在☉O上,BD是☉O的直径,∠CBD=21°,则∠A的度数为 .?
11.如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是 °.?
12.如图,一块三角尺ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD= °.?
13.如图,图中有多少个圆周角?所对的圆周角有几个?所对的圆周角有几个?
14.如图所示,已知四边形ABCD的四个顶点均在☉O上,AB=BC,BD交AC于点E.
求证:DB平分∠ADC.
15.如图所示,四边形ABCD内接于☉O,∠B=50°,∠ACD=25°,∠BAD=65°.
求证:(1)AD=CD;
(2)AB是☉O的直径.
16.
如图,☉O的弦AB,CD的延长线相交于点P,且AB=CD.求证:PA=PC.
17.如图,已知AB为☉O的直径,AB=AC,BC交☉O于点D,AC交☉O于点E,∠BAC=45°.
(1)求∠EBC的度数;
(2)求证:BD=CD.
18.如图,MN是☉O的直径,MN=4,点A在☉O上,∠AMN=30°,B为的中点,P是直径MN上一动点.
(1)利用尺规作图,确定当PA+PB最小时点P的位置(不写作法,但要保留作图痕迹);
(2)求PA+PB的最小值.
答案
1-6.CDDADD
7.30
8.2
9.50 .
10.69° .
11.120 .
12.61
13.解:图中有8个圆周角,所对的圆周角有1个,是∠BDC;所对的圆周角有2个,分别是∠CBD,∠CAD.
14.证明:∵AB=BC,∴=,
∴∠ADB=∠BDC,
即DB平分∠ADC.
15.证明:(1)∵四边形ABCD内接于☉O,
∴∠D=180°-∠B=130°.
又∵∠ACD=25°,
∴∠DAC=180°-∠D-∠ACD=180°-130°-25°=25°,
∴∠DAC=∠ACD,∴AD=CD.
(2)∵∠BAC=∠BAD-∠DAC=65°-25°=40°,∠B=50°,
∴∠ACB=180°-∠B-∠BAC=180°-50°-40°=90°,
∴AB是☉O的直径.
16.证明:如图,连接AC.
∵AB=CD,
∴=,
∴+=+,
即=,
∴∠C=∠A,
∴PA=PC.
17.解:(1)∵AB是☉O的直径,
∴∠AEB=90°.
又∵∠BAC=45°,∴∠ABE=45°.
∵AB=AC,∴∠ABC=∠C=67.5°,
∴∠EBC=∠ABC-∠ABE=67.5°-45°=22.5°.
(2)证明:连接AD.
∵AB是☉O的直径,
∴∠ADB=90°,∴AD⊥BC.
又∵AB=AC,
∴BD=CD.
18.解:(1)如图,点P即为所求.
(2)如图,连接OA,OA',OB.
由(1)可得PA+PB的最小值即为线段A'B的长.∵点A'和点A关于MN对称且∠AMN=30°,∴∠AON=∠A'ON=2∠AMN=60°.又∵B为的中点,∴∠BON=∠AON=30°,∴∠A'OB=90°.∵MN=4,∴OB=OA'=2.在Rt△A'OB中,由勾股定理得A'B==2,∴PA+PB的最小值是2.
1.下列四个图中,∠α是圆周角的是
( )
2.
如图,A,B,C,D是圆上的点,则图中与∠A相等的角是
( )
A.∠B
B.∠C
C.∠DEB
D.∠D
3如图,四边形ABCD内接于☉O,若∠A=40°,则∠C的度数为( )
A.110°
B.120°
C.135°
D.140°
4
如图△ABC的三个顶点都在☉O上,AB=AC,∠BCA=65°,作CD∥AB,并与☉O相交于点D,连接BD,则∠DBC的度数为( )
A.15°
B.35°
C.25°
D.45°
5.如图,点A,B,C在☉O上,∠AOB=72°,则∠ACB等于( )
A.28°
B.54°
C.18°
D.36°
6.如图所示,把一个量角器放置在△ABC的上面,根据量角器的读数可得∠BAC的度数是( )
A.60°
B.30°
C.20°
D.15°
7.如图,AB是☉O的直径,C,D是☉O上的两点,∠AOC=120°,则∠CDB= °.?
8.如图,在☉O中,半径OC⊥弦AB于点D,点E在☉O上,∠E=22.5°,AB=4,则半径OB= .?
9.如图已知AB是☉O的直径,点C在☉O上,若∠CAB=40°,则∠ABC= °.?
10
如图,△ABC的顶点都在☉O上,BD是☉O的直径,∠CBD=21°,则∠A的度数为 .?
11.如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是 °.?
12.如图,一块三角尺ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD= °.?
13.如图,图中有多少个圆周角?所对的圆周角有几个?所对的圆周角有几个?
14.如图所示,已知四边形ABCD的四个顶点均在☉O上,AB=BC,BD交AC于点E.
求证:DB平分∠ADC.
15.如图所示,四边形ABCD内接于☉O,∠B=50°,∠ACD=25°,∠BAD=65°.
求证:(1)AD=CD;
(2)AB是☉O的直径.
16.
如图,☉O的弦AB,CD的延长线相交于点P,且AB=CD.求证:PA=PC.
17.如图,已知AB为☉O的直径,AB=AC,BC交☉O于点D,AC交☉O于点E,∠BAC=45°.
(1)求∠EBC的度数;
(2)求证:BD=CD.
18.如图,MN是☉O的直径,MN=4,点A在☉O上,∠AMN=30°,B为的中点,P是直径MN上一动点.
(1)利用尺规作图,确定当PA+PB最小时点P的位置(不写作法,但要保留作图痕迹);
(2)求PA+PB的最小值.
答案
1-6.CDDADD
7.30
8.2
9.50 .
10.69° .
11.120 .
12.61
13.解:图中有8个圆周角,所对的圆周角有1个,是∠BDC;所对的圆周角有2个,分别是∠CBD,∠CAD.
14.证明:∵AB=BC,∴=,
∴∠ADB=∠BDC,
即DB平分∠ADC.
15.证明:(1)∵四边形ABCD内接于☉O,
∴∠D=180°-∠B=130°.
又∵∠ACD=25°,
∴∠DAC=180°-∠D-∠ACD=180°-130°-25°=25°,
∴∠DAC=∠ACD,∴AD=CD.
(2)∵∠BAC=∠BAD-∠DAC=65°-25°=40°,∠B=50°,
∴∠ACB=180°-∠B-∠BAC=180°-50°-40°=90°,
∴AB是☉O的直径.
16.证明:如图,连接AC.
∵AB=CD,
∴=,
∴+=+,
即=,
∴∠C=∠A,
∴PA=PC.
17.解:(1)∵AB是☉O的直径,
∴∠AEB=90°.
又∵∠BAC=45°,∴∠ABE=45°.
∵AB=AC,∴∠ABC=∠C=67.5°,
∴∠EBC=∠ABC-∠ABE=67.5°-45°=22.5°.
(2)证明:连接AD.
∵AB是☉O的直径,
∴∠ADB=90°,∴AD⊥BC.
又∵AB=AC,
∴BD=CD.
18.解:(1)如图,点P即为所求.
(2)如图,连接OA,OA',OB.
由(1)可得PA+PB的最小值即为线段A'B的长.∵点A'和点A关于MN对称且∠AMN=30°,∴∠AON=∠A'ON=2∠AMN=60°.又∵B为的中点,∴∠BON=∠AON=30°,∴∠A'OB=90°.∵MN=4,∴OB=OA'=2.在Rt△A'OB中,由勾股定理得A'B==2,∴PA+PB的最小值是2.
同课章节目录
