人教版七年级数学上册课件:1.3.1有理数的加法 课件(20张ppt)
文档属性
| 名称 | 人教版七年级数学上册课件:1.3.1有理数的加法 课件(20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
1、同号两数相加,取相同的符号,并
把绝对值相加。
2、异号两数相加,取绝对值较大的加
数的符号,并用较大的绝对值减去
较小的绝对值。
3、互为相反数的两个数相加得0。
4、一个数同0相加,仍得这个数。
有理数加法法则
复习:
问题1:在小学中我们学过哪些加法的运算律?
问题2:加法的运算律是不是也可以扩充到
有理数范围?
有理数的加法(二)
——运算律探索
学习目标:
1.
经历探索有理数加法的运算律的过程,并能利用加法的运算律进行简化计算。
2.能利用有理数加法的的意义,解决实际问题。
3.通过一些具体数的计算,合情推理,归纳出有理数的加法的运算律。
4.鼓励学生利用运算律进行简便计算,让学生养成求简意识。
重点:探索有理数加法的运算律,并能运用有理数加法运算。
难点:用有理数加法解决实际问题。
自学提纲:
1、请完成下列计算
(1)(-8)+(-9)
(-9)+(-8)
(2)
4+(-7)
(-7)+4
(3)
6+(-2)
(-2)+6
(4)
[2+(-3)]+(-8)
2+[(-3)+(-8)]
(5)
10+[(-10)+(-5)]
[10+(-10)]+(-5)
2、两个运算律的符号表示与文字表示分别是什么?
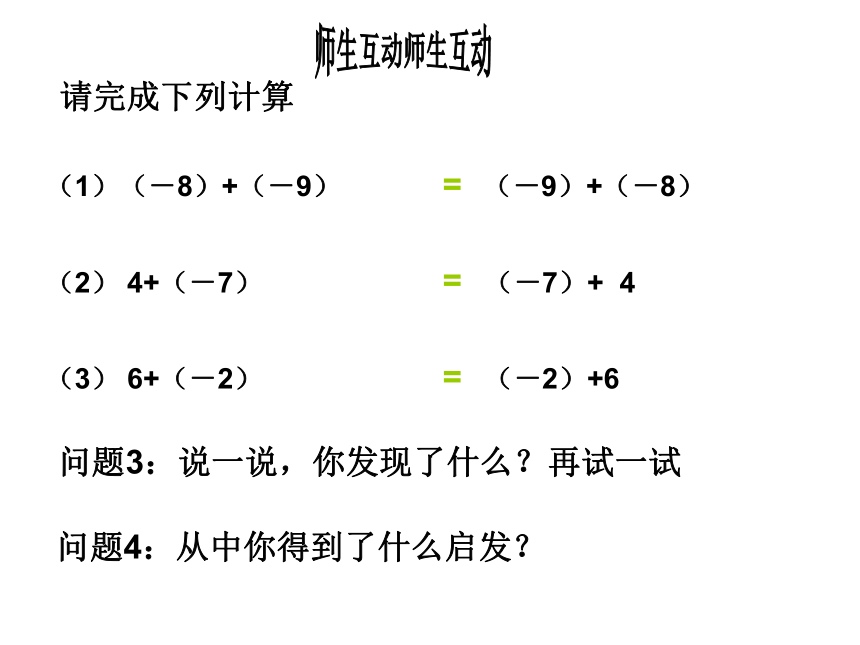
请完成下列计算
(1)(-8)+(-9)
(-9)+(-8)
(2)
4+(-7)
(-7)+
4
(3)
6+(-2)
(-2)+6
=
=
=
问题3:说一说,你发现了什么?再试一试
问题4:从中你得到了什么启发?
师生互动
有理数的加法中,两个数相加,交换加数
的位置和不变。
加法交换律:a+b=b+a
完成下列计算:
(1)
[2+(-3)]+(-8)
2+[(-3)+(-8)]
(2)
10+[(-10)+(-5)]
[10+(-10)]+(-5)
问题4:从中你得到了什么启发?
问题3:说一说,你发现了什么?再试一试
=
=
合作探究
有理数加法中,三个数相加,先把前两个数相加,
或者先把后两个数相加,和不变。
加法的结合律:(a+b)+c=a+(b+c)
问题5:为什么我们要学习加法的运算律呢?
例1
计算:16+(-25)+24+(-35)
问题6:此题你是抓住数的什么特点使计算简化的?
依据是什么?
解:原式=16+24+(-25)+(-35)
=(16+24)+[(-25)+(-35)]
=40+(-60)
=-20
做下面的练习,并思考你是如何使计算简化的?
(1)23+(-17)+6+(-22)
(2)(-2)+3+1+(-3)+2+(-4)
(3)9+(-6.82)+3.78+(-3.18)+(-3.78)
(4)
使用运算律通常有下列情形:
(1)互为相反数的两个数可先相加;
(2)几个数相加得整数时,可先相加;
(3)同分母的分数可以先相加;
(4)符号相同的数可以先相加。
小
结
一、加法的运算律
1、加法交换律:
两个数相加,交换加数的位置,和不变。a+b=b+a
2、加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.(a+b)+c=a+(b+c)
二、使用运算律通常有下列情形:
(1)互为相反数的两个数可先相加;
(2)几个数相加得整数时,可先相加;
(3)同分母的分数可以先相加;
(4)符号相同的数可以先相加。
1.用简便方法计算:
(1)(+45.3)+(-9.5)+(+4.7)
(2)(+2.5)+(+3
)+(+1
)+1
—
5
6
—
1
2
—
1
6
当堂达标
(1)15+(-13)+18
(2)(-2.48)+4.33+(-7.52)+(-4.33)
(3)
2、计算
解:原式=(15+18)+(-13)
=33+(-13)
=20
解:原式=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]
=(-10)+0
=-10
3、练习:
下陈中学食堂为了供我们同学吃饭,在市场上购进8袋大米,由于当时没带秤,他就以每袋大米为90千克作为标准重量交易。事后,食堂人员称了一下,8袋大米的称重如下:91、89、91.2、91.3、88.7、88.8、91.8、91.1(单位:千克)。请你帮食堂算一算,他是赚了还是亏了?赚或亏了多少?8袋大米的实际总重量是多少?
1、小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15m,再向西行驶25m,然后又向东行驶20m,再向西行驶35m,问玩具赛车最后停在何处?一共行驶了多少米?
拓展提高
解:记向东为正,根据题意得:
(1)、(+15)+(-25)+(+20)+(-35)
=-25
(2)、|+15|+|-25|+|+20|+|-35|
=95
答:小明的遥控车最后停在小明的西边25米处,
一共行驶了95千米。
2.
蚂蚁从某点O出发在一条直线上来回爬行,假定向右爬行的路程为正数,向左爬行的路程为负数,爬过的各段路程依次为(单位:厘米)
+6,-3,+10,-5,-7,+13,-10
(1)蚂蚁最后是否回到了出发点?
(2)蚂蚁离开出发点O最远是多少厘米?
(3)在爬行过程中,如果爬行1厘米奖励一粒芝麻,则蚂蚁一共得到多少粒芝麻?
+4
13厘米
54粒
通过本节学习,你有什么收获?
布置作业
1、习题1.3第2题
2、
谢
谢!
1、同号两数相加,取相同的符号,并
把绝对值相加。
2、异号两数相加,取绝对值较大的加
数的符号,并用较大的绝对值减去
较小的绝对值。
3、互为相反数的两个数相加得0。
4、一个数同0相加,仍得这个数。
有理数加法法则
复习:
问题1:在小学中我们学过哪些加法的运算律?
问题2:加法的运算律是不是也可以扩充到
有理数范围?
有理数的加法(二)
——运算律探索
学习目标:
1.
经历探索有理数加法的运算律的过程,并能利用加法的运算律进行简化计算。
2.能利用有理数加法的的意义,解决实际问题。
3.通过一些具体数的计算,合情推理,归纳出有理数的加法的运算律。
4.鼓励学生利用运算律进行简便计算,让学生养成求简意识。
重点:探索有理数加法的运算律,并能运用有理数加法运算。
难点:用有理数加法解决实际问题。
自学提纲:
1、请完成下列计算
(1)(-8)+(-9)
(-9)+(-8)
(2)
4+(-7)
(-7)+4
(3)
6+(-2)
(-2)+6
(4)
[2+(-3)]+(-8)
2+[(-3)+(-8)]
(5)
10+[(-10)+(-5)]
[10+(-10)]+(-5)
2、两个运算律的符号表示与文字表示分别是什么?
请完成下列计算
(1)(-8)+(-9)
(-9)+(-8)
(2)
4+(-7)
(-7)+
4
(3)
6+(-2)
(-2)+6
=
=
=
问题3:说一说,你发现了什么?再试一试
问题4:从中你得到了什么启发?
师生互动
有理数的加法中,两个数相加,交换加数
的位置和不变。
加法交换律:a+b=b+a
完成下列计算:
(1)
[2+(-3)]+(-8)
2+[(-3)+(-8)]
(2)
10+[(-10)+(-5)]
[10+(-10)]+(-5)
问题4:从中你得到了什么启发?
问题3:说一说,你发现了什么?再试一试
=
=
合作探究
有理数加法中,三个数相加,先把前两个数相加,
或者先把后两个数相加,和不变。
加法的结合律:(a+b)+c=a+(b+c)
问题5:为什么我们要学习加法的运算律呢?
例1
计算:16+(-25)+24+(-35)
问题6:此题你是抓住数的什么特点使计算简化的?
依据是什么?
解:原式=16+24+(-25)+(-35)
=(16+24)+[(-25)+(-35)]
=40+(-60)
=-20
做下面的练习,并思考你是如何使计算简化的?
(1)23+(-17)+6+(-22)
(2)(-2)+3+1+(-3)+2+(-4)
(3)9+(-6.82)+3.78+(-3.18)+(-3.78)
(4)
使用运算律通常有下列情形:
(1)互为相反数的两个数可先相加;
(2)几个数相加得整数时,可先相加;
(3)同分母的分数可以先相加;
(4)符号相同的数可以先相加。
小
结
一、加法的运算律
1、加法交换律:
两个数相加,交换加数的位置,和不变。a+b=b+a
2、加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.(a+b)+c=a+(b+c)
二、使用运算律通常有下列情形:
(1)互为相反数的两个数可先相加;
(2)几个数相加得整数时,可先相加;
(3)同分母的分数可以先相加;
(4)符号相同的数可以先相加。
1.用简便方法计算:
(1)(+45.3)+(-9.5)+(+4.7)
(2)(+2.5)+(+3
)+(+1
)+1
—
5
6
—
1
2
—
1
6
当堂达标
(1)15+(-13)+18
(2)(-2.48)+4.33+(-7.52)+(-4.33)
(3)
2、计算
解:原式=(15+18)+(-13)
=33+(-13)
=20
解:原式=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]
=(-10)+0
=-10
3、练习:
下陈中学食堂为了供我们同学吃饭,在市场上购进8袋大米,由于当时没带秤,他就以每袋大米为90千克作为标准重量交易。事后,食堂人员称了一下,8袋大米的称重如下:91、89、91.2、91.3、88.7、88.8、91.8、91.1(单位:千克)。请你帮食堂算一算,他是赚了还是亏了?赚或亏了多少?8袋大米的实际总重量是多少?
1、小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15m,再向西行驶25m,然后又向东行驶20m,再向西行驶35m,问玩具赛车最后停在何处?一共行驶了多少米?
拓展提高
解:记向东为正,根据题意得:
(1)、(+15)+(-25)+(+20)+(-35)
=-25
(2)、|+15|+|-25|+|+20|+|-35|
=95
答:小明的遥控车最后停在小明的西边25米处,
一共行驶了95千米。
2.
蚂蚁从某点O出发在一条直线上来回爬行,假定向右爬行的路程为正数,向左爬行的路程为负数,爬过的各段路程依次为(单位:厘米)
+6,-3,+10,-5,-7,+13,-10
(1)蚂蚁最后是否回到了出发点?
(2)蚂蚁离开出发点O最远是多少厘米?
(3)在爬行过程中,如果爬行1厘米奖励一粒芝麻,则蚂蚁一共得到多少粒芝麻?
+4
13厘米
54粒
通过本节学习,你有什么收获?
布置作业
1、习题1.3第2题
2、
谢
谢!
