人教版九年级数学上册24.1.2 垂直于弦的直径同步练习(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学上册24.1.2 垂直于弦的直径同步练习(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 206.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-17 00:00:00 | ||
图片预览


文档简介
24.1.2 垂直于弦的直径
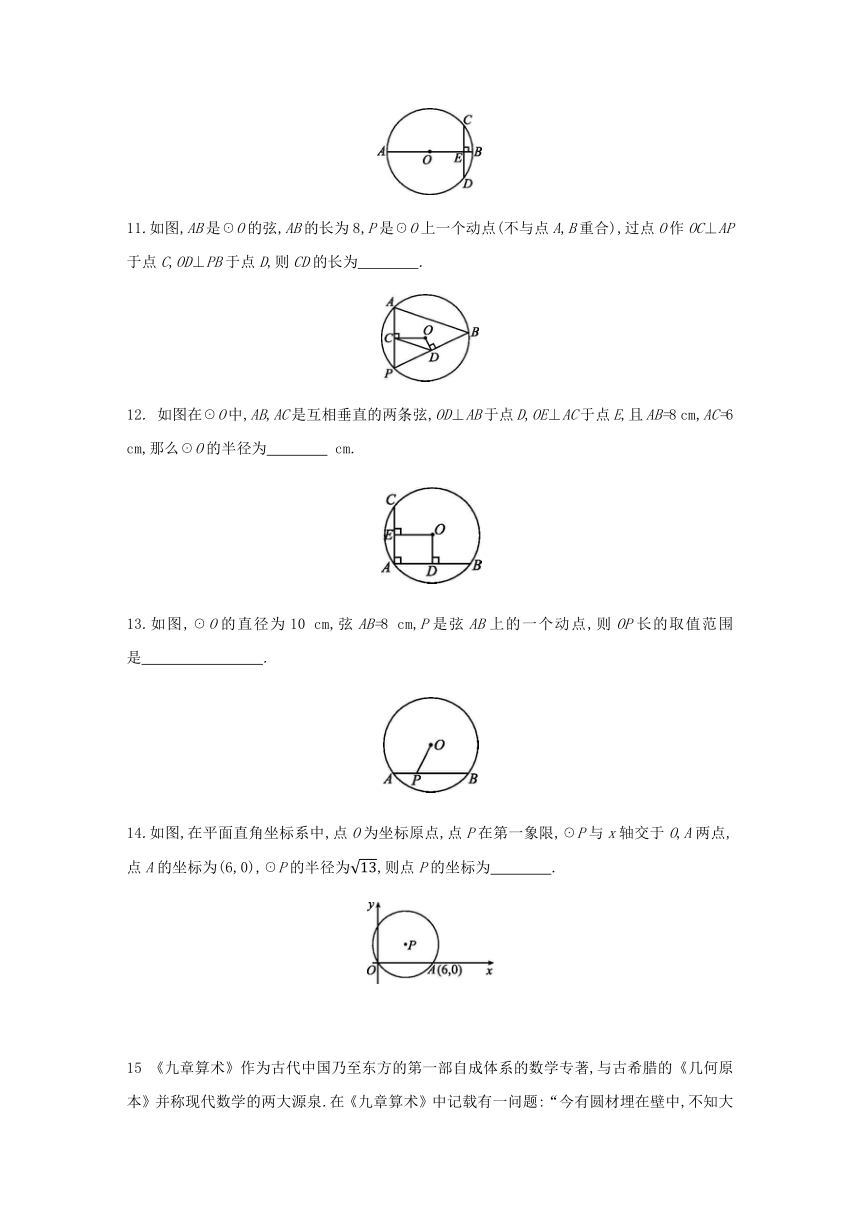
1.下列说法中,不正确的是( )
A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都会与自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴
2.如图,AB是☉O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是
( )
A.CM=DM
B.=
C.=
D.OM=MB
3.如图,☉O的半径为13,弦AB的长是24,ON⊥AB,垂足为N,则ON的长为
( )
A.5
B.7
C.9
D.11
4.如图,AB是☉O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是( )
A.
B.2
C.6
D.8
5.如图,在☉O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是
( )
A.3
B.2.5
C.2
D.1
6.下列说法正确的是
( )
A.垂直于弦的直线平分弦所对的两条弧
B.平分弦的直径垂直于弦
C.垂直于直径的弦平分这条直径
D.过弦(不是直径)的中点的直径平分弦所对的两条弧
7.如图所示,☉O的直径CD=10
cm,AB是☉O的弦,AM=BM,OM∶OC=3∶5,则AB的长为( )
A.8
cm
B.
cm
C.6
cm
D.2
cm
8.如图,☉O的半径OA=6,以点A为圆心,OA长为半径的弧交☉O于B,C两点,则BC的长等于( )
A.6
B.6
C.3
D.3
9.已知☉O的半径为13
cm,弦AB∥CD,AB=24
cm,CD=10
cm,则AB与CD之间的距离为( )
A.17
cm
B.7
cm
C.12
cm
D.17
cm或7
cm
10.如图,AB为☉O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则☉O的半径为 .?
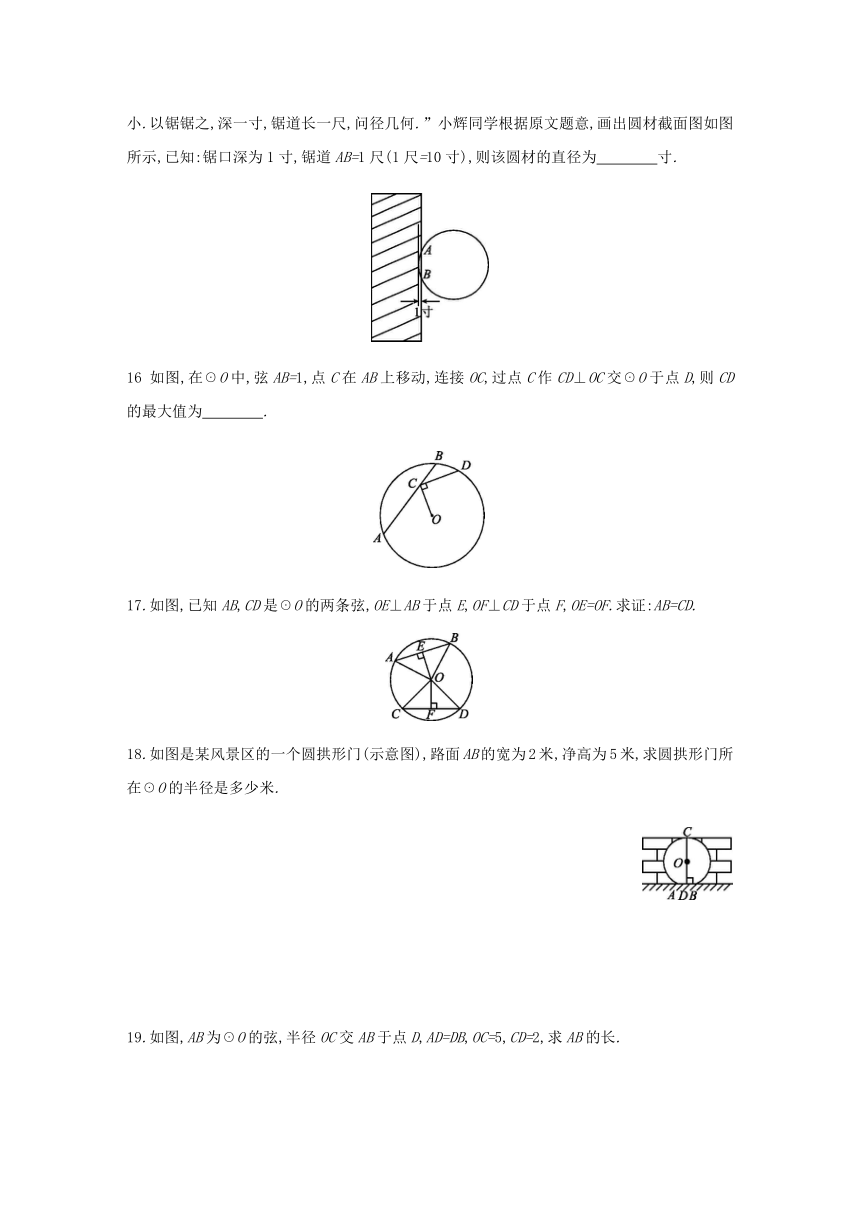
11.如图,AB是☉O的弦,AB的长为8,P是☉O上一个动点(不与点A,B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为 .?
12.
如图在☉O中,AB,AC是互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,且AB=8
cm,AC=6
cm,那么☉O的半径为
cm.?
13.如图,☉O的直径为10
cm,弦AB=8
cm,P是弦AB上的一个动点,则OP长的取值范围是 .?
14.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,☉P与x轴交于O,A两点,点A的坐标为(6,0),☉P的半径为,则点P的坐标为 .?
15
《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何.”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为 寸.?
16
如图,在☉O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 .?
17.如图,已知AB,CD是☉O的两条弦,OE⊥AB于点E,OF⊥CD于点F,OE=OF.求证:AB=CD.
18.如图是某风景区的一个圆拱形门(示意图),路面AB的宽为2米,净高为5米,求圆拱形门所在☉O的半径是多少米.
19.如图,AB为☉O的弦,半径OC交AB于点D,AD=DB,OC=5,CD=2,求AB的长.
20.如图,圆柱形水管内原有积水的水平面宽CD=20
cm,水深GF=2
cm,若水面上升2
cm,则此时水面宽AB为多少?
24.1.2 垂直于弦的直径
1.D
2.D 3.A 4.B 5.C 5.D
7.A 8.A 9.D
10.5
11.
4
12.5
13.3
cm≤OP≤5
cm
14.(3,2)
15.26
16.
17.证明:∵OE⊥AB,OF⊥CD,
∴AE=BE,CF=DF.
在Rt△OBE与Rt△ODF中,
∴Rt△OBE≌Rt△ODF(HL),
∴BE=DF,∴2BE=2DF,即AB=CD.
18.解:连接OA,如图.
∵CD⊥AB,且CD过圆心O,∴AD=AB=1米,∠CDA=90°.设☉O的半径为R米,则OA=OC=R米,OD=(5-R)米.
在Rt△OAD中,由勾股定理,得OA2=OD2+AD2,即R2=(5-R)2+12,解得R=2.6.故圆拱形门所在☉O的半径为2.6米.
19.解:连接OB,如图所示.
∵☉O的半径为5,CD=2,
∴OD=5-2=3.
∵AD=DB,
∴OC⊥AB,
∴∠ODB=90°,
∴BD===4,
∴AB=2BD=8.
20.解:如图所示,连接OA,OC.
设OA=OC=OF=R
cm.
∵GF=2
cm,
∴OG=(R-2)cm.
∵CD=20
cm,∴CG=10
cm.
在Rt△OGC中,OG2+CG2=OC2,
即(R-2)2+102=R2,
解得R=26.
当水面上升2
cm时,OE=26-4=22(cm),
则AE===8(cm),∴AB=2AE=16
cm.
答:此时水面宽AB是16
cm.
1.下列说法中,不正确的是( )
A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都会与自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴
2.如图,AB是☉O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是
( )
A.CM=DM
B.=
C.=
D.OM=MB
3.如图,☉O的半径为13,弦AB的长是24,ON⊥AB,垂足为N,则ON的长为
( )
A.5
B.7
C.9
D.11
4.如图,AB是☉O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是( )
A.
B.2
C.6
D.8
5.如图,在☉O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是
( )
A.3
B.2.5
C.2
D.1
6.下列说法正确的是
( )
A.垂直于弦的直线平分弦所对的两条弧
B.平分弦的直径垂直于弦
C.垂直于直径的弦平分这条直径
D.过弦(不是直径)的中点的直径平分弦所对的两条弧
7.如图所示,☉O的直径CD=10
cm,AB是☉O的弦,AM=BM,OM∶OC=3∶5,则AB的长为( )
A.8
cm
B.
cm
C.6
cm
D.2
cm
8.如图,☉O的半径OA=6,以点A为圆心,OA长为半径的弧交☉O于B,C两点,则BC的长等于( )
A.6
B.6
C.3
D.3
9.已知☉O的半径为13
cm,弦AB∥CD,AB=24
cm,CD=10
cm,则AB与CD之间的距离为( )
A.17
cm
B.7
cm
C.12
cm
D.17
cm或7
cm
10.如图,AB为☉O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则☉O的半径为 .?
11.如图,AB是☉O的弦,AB的长为8,P是☉O上一个动点(不与点A,B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为 .?
12.
如图在☉O中,AB,AC是互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,且AB=8
cm,AC=6
cm,那么☉O的半径为
cm.?
13.如图,☉O的直径为10
cm,弦AB=8
cm,P是弦AB上的一个动点,则OP长的取值范围是 .?
14.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,☉P与x轴交于O,A两点,点A的坐标为(6,0),☉P的半径为,则点P的坐标为 .?
15
《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何.”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为 寸.?
16
如图,在☉O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交☉O于点D,则CD的最大值为 .?
17.如图,已知AB,CD是☉O的两条弦,OE⊥AB于点E,OF⊥CD于点F,OE=OF.求证:AB=CD.
18.如图是某风景区的一个圆拱形门(示意图),路面AB的宽为2米,净高为5米,求圆拱形门所在☉O的半径是多少米.
19.如图,AB为☉O的弦,半径OC交AB于点D,AD=DB,OC=5,CD=2,求AB的长.
20.如图,圆柱形水管内原有积水的水平面宽CD=20
cm,水深GF=2
cm,若水面上升2
cm,则此时水面宽AB为多少?
24.1.2 垂直于弦的直径
1.D
2.D 3.A 4.B 5.C 5.D
7.A 8.A 9.D
10.5
11.
4
12.5
13.3
cm≤OP≤5
cm
14.(3,2)
15.26
16.
17.证明:∵OE⊥AB,OF⊥CD,
∴AE=BE,CF=DF.
在Rt△OBE与Rt△ODF中,
∴Rt△OBE≌Rt△ODF(HL),
∴BE=DF,∴2BE=2DF,即AB=CD.
18.解:连接OA,如图.
∵CD⊥AB,且CD过圆心O,∴AD=AB=1米,∠CDA=90°.设☉O的半径为R米,则OA=OC=R米,OD=(5-R)米.
在Rt△OAD中,由勾股定理,得OA2=OD2+AD2,即R2=(5-R)2+12,解得R=2.6.故圆拱形门所在☉O的半径为2.6米.
19.解:连接OB,如图所示.
∵☉O的半径为5,CD=2,
∴OD=5-2=3.
∵AD=DB,
∴OC⊥AB,
∴∠ODB=90°,
∴BD===4,
∴AB=2BD=8.
20.解:如图所示,连接OA,OC.
设OA=OC=OF=R
cm.
∵GF=2
cm,
∴OG=(R-2)cm.
∵CD=20
cm,∴CG=10
cm.
在Rt△OGC中,OG2+CG2=OC2,
即(R-2)2+102=R2,
解得R=26.
当水面上升2
cm时,OE=26-4=22(cm),
则AE===8(cm),∴AB=2AE=16
cm.
答:此时水面宽AB是16
cm.
同课章节目录
