人教版七年级数学上册课件:1.3.2有理数的减法(26张)
文档属性
| 名称 | 人教版七年级数学上册课件:1.3.2有理数的减法(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
1.3.2有理数的减法
(2
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
(3)
一个数与0相加,仍得这个数.
(1)
4
+
16
=
(2)(–2)+(–27)=
(3)
(–9)+
10
=
(4)
45
+
(–60)
=
(5)
(–7)+
7
=
(6)
16
+
0
=
(7)
0
+
(–8)
=
20
–29
1
–15
16
–8
(1)
同号两数相加,取相同的符号,并把绝对值相加.
0
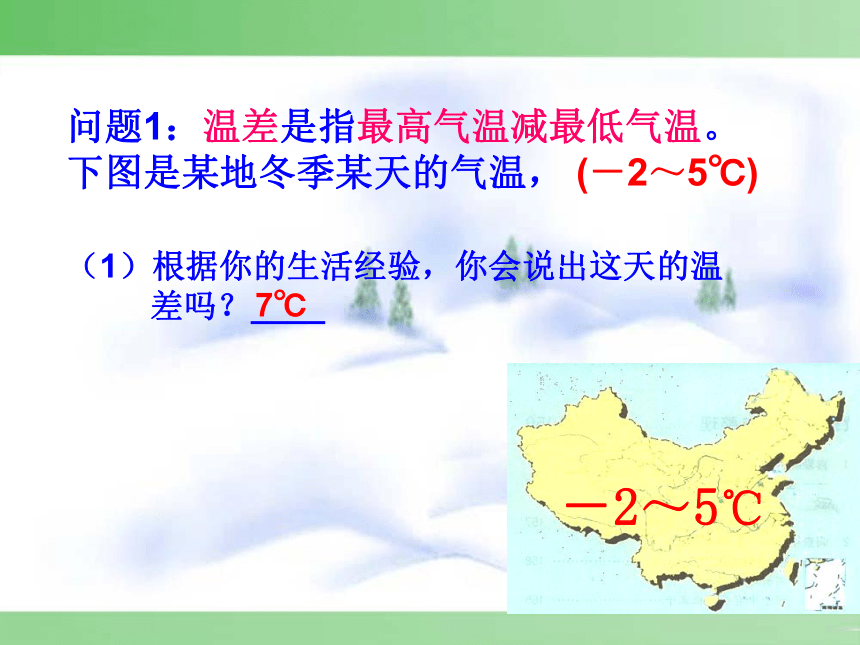
-2~5℃
问题1:温差是指最高气温减最低气温。下图是某地冬季某天的气温,
(-2~5℃)
(1)根据你的生活经验,你会说出这天的温
差吗?____
7℃
7
5-(-2)=7℃
0
-2
-5
5
(2)你还能从温度计上看出5℃比
-2℃高_____℃吗?
(3)请列式求该天该地的温差?
7
列成算式为:____________
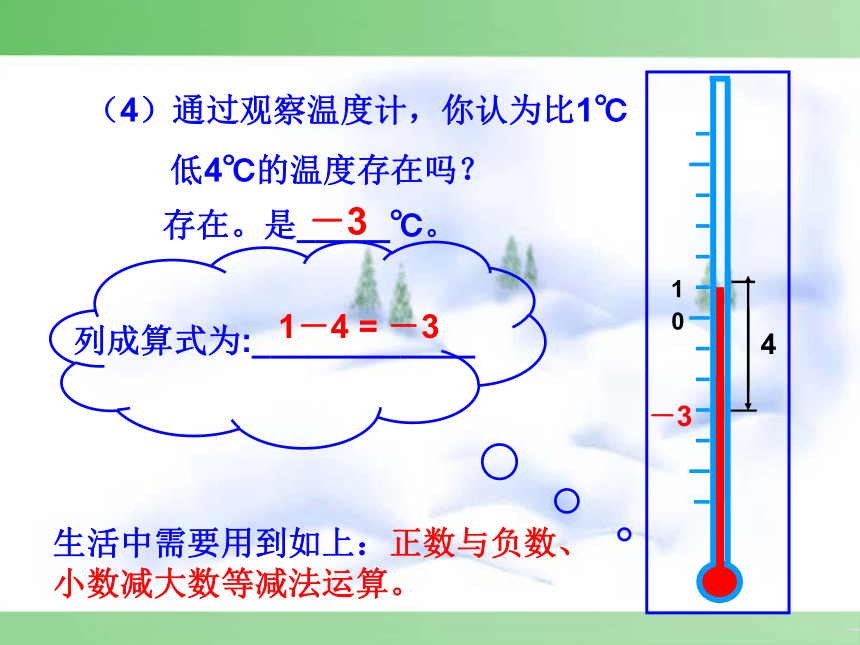
4
(4)通过观察温度计,你认为比1℃
低4℃的温度存在吗?
存在。是_____℃。
1-4
=
-3
生活中需要用到如上:正数与负数、小数减大数等减法运算。
-3
-3
0
1
有理数的减法
学习目标:
知识技能
1、理解并掌握有理数的减法法则
2、会进行有理数的减法运算。
过程方法
体会渗透划归的思想,把减法运算转化为加法运算
情感态度
通过师生合作,学生自我探究,让学生充分参与到数学学习的过程来。
教学重点与难点:
重点:会用有理数减法法则进行运算。
难点:探索有理数减法法则,实现减法到
加法的转化。
学习目标
重点难点
1、预习课本第21-22页
2、思考课本第22页探究,观察结果并总结有理数的减法法则
学
习
提
纲
被减数-减数=差
差+减数=被减数
要计算5-(-2)=差
就是要求一个差x,使得x与减数-2相加得被减数5。
因为__+(-2)=5
所以差x应该是7,即
5-(-2)=7
我们还知道
(+2)
由①②有
5-(-2)=5+(+2)
①
②
5-(-2)
=
?
7
5
+
=7
5-(-2)=5+(+2)
这个等式能说明什么?
说明减-2相当于加+2
0-(-2)
=
?
(-1)-(-2)
=
?
要计算0-(-2)=差
就是要求一个差x,使得x与减数-2相加得被减数0。
因为__+(-2)=0
所以差x应该是2,即
0-(-2)=2
我们还知道
(+2)
由①②有
0-(-2)=0+(+2)
①
②
0-(-2)
=
?
2
0
+
=2
要计算(-1)-(-2)=差
就是要求一个差x,使得x与减数-2相加得被减数1。
因为__+(-2)=-1
所以差x应该是1,即
(-1)-(-2)=1
我们还知道
(+2)
由①②有
(-1)-(-2)=(-1)+(+2)
①
②
(-1)-(-2)
=
?
1
(-1)
+
=1
5-(-2)=5+(+2)
0-(-2)=0+(+2)
(-1)-(-2)=(-1)+(+2)
(-2)
(-2)
(-2)
(+2)
(+2)
(+2)
这个等式能说明:
减-2相当于加____。
+2
计算下列各式:
50-20=
50+(-20)=
50-10=
50+(-10)=
50-0
=
50+
0
=
50-(-10)=
50+10=
50-(-20)=
50+20=
30
30
40
40
50
50
60
60
70
70
有理数减法法则
减去一个数,等于加上这个数的相反数
注意:减法在运算时有
2
个要素要发生变化。
1
减
加
2
数
相反数
练习:
1
(-2)
–
(-
3)
=(
-
2)
+
(
)
2
0
–
(
-
4)
=
0
+
(
)
3
(
-
6)
–
3=
(
-
6)
+
(
)
4
1
–
(+39)
=
1
+
(
)
下列括号内填数
+4
+3
-3
-39
例1
计算下列各题:
(1)9
-(-5)
(2)(-3)-
1
(3)0
–
8
(4)(-5)
-
0
(2)原式=(-3)+(-1)
=-4
解:(1)原式=
9
+
5
=
14
减去1等于加上
1
的相反数。
(3)原式
=
0
+(-8)=
-
8
(4)原式
=(-5
)+
0
=
-5
减去(-5)等于加上
-5
的相反数。
说明:
1.
0减去一个数,等于这个数的相反数。
2.
一个数减去0,仍然等于这个数。
利用减法法则,计算下列各题
(1)
0
–
(+5)
(2)
0
–
(-2.3)
利用减法法则,计算下列各题
(1)
-
4
-
0
(2)
+1.5
-
0
=0+(-5)=-5
=0+2.3=2.3
=-4
=+1.5
2、
计算下列各式:
(1)5
–
(–
15)
(2)0–
7
–
5
(3)(
–
1.3
)–(
–
2.1)
(4)
1、
计算下列各式:
(1)-3
–
(–
5);
(2)0
-
7
(3)7.2-(-
4.8)
;
(4
)(
–
3
)
–
5
计算(学生板演)
随堂练习
例2
世界上最高的山峰是珠穆朗玛峰,
其海拔高度是
8844
米,吐鲁番盆地的海拔高度是
–155
米,两处高度相差多少米?
解:8844-(-155)
=8844+155
=8999(米)
答:两处高度相差8999米。
1.
一个数是18,另一个数比这个数的相反数小3,求另一个数.
变式2:一个数的相反数是18,另一个数的绝对值是3,
求这两个数的差.
解:-18-3=-21
解:-18-3=-21或:-18-(-3)=-15
变式1:一个数是-18,另一个数比这个数的绝对值
的2倍小-5,求另一个数
2、求比-3
℃低6
℃的温度。
当堂达标:
1、求比2℃低8
℃
的温度。
2-8=2+(-8)=-6
℃
-3-6=(-3)+(-6)=-9
℃
-392
392
死海
3、如图,世界上最高峰是珠穆朗玛峰,陆上最低处是死海(位于亚洲西部的一个湖泊)求两处高度相差多少?
8848-(-392)
=9240(米)
=8848+(+392)
答:两处高度差为9240米.
4、选择题:
(1)较小的数减去较大的数,所得的数一定是(
)
A
0
B
正数
C
负数
D
0或负数
(2)下列说法正确的是(
)
A
减去一个
负数,差一定大于被减数;
B
减去一个正数,差不一定小于被减数;
C
0
减去任何数,差都是负数;
D
两个数之差一定小于被减数;
C
A
(3)下列说法正确的是(
)
A
减去一个数,等于加上这个数;
B
有理数的减法中,被减数不一定比减数大;
C
0
减去一个数
,仍得
这个数;
D
两个相反数相减得
0
;
(4)差是-5,被减数是-2,则减数为(
)
A
-7
B
-3
C
3
D
-7
B
C
1、有理数减法的意义
2、有理数的减法法则
小结
3、有理数的减法的运算步骤
注意点:
1、被减数与减数的位置不能互换
2、减法法则不能与加法法则中的两个异号的数相加混淆。
3、不存在“不够减”的问题(可用作差法比较两个有理数的大小)
作业:
必做:课本P25第3、4
选作:导学与训练
1.3.2有理数的减法
(2
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
(3)
一个数与0相加,仍得这个数.
(1)
4
+
16
=
(2)(–2)+(–27)=
(3)
(–9)+
10
=
(4)
45
+
(–60)
=
(5)
(–7)+
7
=
(6)
16
+
0
=
(7)
0
+
(–8)
=
20
–29
1
–15
16
–8
(1)
同号两数相加,取相同的符号,并把绝对值相加.
0
-2~5℃
问题1:温差是指最高气温减最低气温。下图是某地冬季某天的气温,
(-2~5℃)
(1)根据你的生活经验,你会说出这天的温
差吗?____
7℃
7
5-(-2)=7℃
0
-2
-5
5
(2)你还能从温度计上看出5℃比
-2℃高_____℃吗?
(3)请列式求该天该地的温差?
7
列成算式为:____________
4
(4)通过观察温度计,你认为比1℃
低4℃的温度存在吗?
存在。是_____℃。
1-4
=
-3
生活中需要用到如上:正数与负数、小数减大数等减法运算。
-3
-3
0
1
有理数的减法
学习目标:
知识技能
1、理解并掌握有理数的减法法则
2、会进行有理数的减法运算。
过程方法
体会渗透划归的思想,把减法运算转化为加法运算
情感态度
通过师生合作,学生自我探究,让学生充分参与到数学学习的过程来。
教学重点与难点:
重点:会用有理数减法法则进行运算。
难点:探索有理数减法法则,实现减法到
加法的转化。
学习目标
重点难点
1、预习课本第21-22页
2、思考课本第22页探究,观察结果并总结有理数的减法法则
学
习
提
纲
被减数-减数=差
差+减数=被减数
要计算5-(-2)=差
就是要求一个差x,使得x与减数-2相加得被减数5。
因为__+(-2)=5
所以差x应该是7,即
5-(-2)=7
我们还知道
(+2)
由①②有
5-(-2)=5+(+2)
①
②
5-(-2)
=
?
7
5
+
=7
5-(-2)=5+(+2)
这个等式能说明什么?
说明减-2相当于加+2
0-(-2)
=
?
(-1)-(-2)
=
?
要计算0-(-2)=差
就是要求一个差x,使得x与减数-2相加得被减数0。
因为__+(-2)=0
所以差x应该是2,即
0-(-2)=2
我们还知道
(+2)
由①②有
0-(-2)=0+(+2)
①
②
0-(-2)
=
?
2
0
+
=2
要计算(-1)-(-2)=差
就是要求一个差x,使得x与减数-2相加得被减数1。
因为__+(-2)=-1
所以差x应该是1,即
(-1)-(-2)=1
我们还知道
(+2)
由①②有
(-1)-(-2)=(-1)+(+2)
①
②
(-1)-(-2)
=
?
1
(-1)
+
=1
5-(-2)=5+(+2)
0-(-2)=0+(+2)
(-1)-(-2)=(-1)+(+2)
(-2)
(-2)
(-2)
(+2)
(+2)
(+2)
这个等式能说明:
减-2相当于加____。
+2
计算下列各式:
50-20=
50+(-20)=
50-10=
50+(-10)=
50-0
=
50+
0
=
50-(-10)=
50+10=
50-(-20)=
50+20=
30
30
40
40
50
50
60
60
70
70
有理数减法法则
减去一个数,等于加上这个数的相反数
注意:减法在运算时有
2
个要素要发生变化。
1
减
加
2
数
相反数
练习:
1
(-2)
–
(-
3)
=(
-
2)
+
(
)
2
0
–
(
-
4)
=
0
+
(
)
3
(
-
6)
–
3=
(
-
6)
+
(
)
4
1
–
(+39)
=
1
+
(
)
下列括号内填数
+4
+3
-3
-39
例1
计算下列各题:
(1)9
-(-5)
(2)(-3)-
1
(3)0
–
8
(4)(-5)
-
0
(2)原式=(-3)+(-1)
=-4
解:(1)原式=
9
+
5
=
14
减去1等于加上
1
的相反数。
(3)原式
=
0
+(-8)=
-
8
(4)原式
=(-5
)+
0
=
-5
减去(-5)等于加上
-5
的相反数。
说明:
1.
0减去一个数,等于这个数的相反数。
2.
一个数减去0,仍然等于这个数。
利用减法法则,计算下列各题
(1)
0
–
(+5)
(2)
0
–
(-2.3)
利用减法法则,计算下列各题
(1)
-
4
-
0
(2)
+1.5
-
0
=0+(-5)=-5
=0+2.3=2.3
=-4
=+1.5
2、
计算下列各式:
(1)5
–
(–
15)
(2)0–
7
–
5
(3)(
–
1.3
)–(
–
2.1)
(4)
1、
计算下列各式:
(1)-3
–
(–
5);
(2)0
-
7
(3)7.2-(-
4.8)
;
(4
)(
–
3
)
–
5
计算(学生板演)
随堂练习
例2
世界上最高的山峰是珠穆朗玛峰,
其海拔高度是
8844
米,吐鲁番盆地的海拔高度是
–155
米,两处高度相差多少米?
解:8844-(-155)
=8844+155
=8999(米)
答:两处高度相差8999米。
1.
一个数是18,另一个数比这个数的相反数小3,求另一个数.
变式2:一个数的相反数是18,另一个数的绝对值是3,
求这两个数的差.
解:-18-3=-21
解:-18-3=-21或:-18-(-3)=-15
变式1:一个数是-18,另一个数比这个数的绝对值
的2倍小-5,求另一个数
2、求比-3
℃低6
℃的温度。
当堂达标:
1、求比2℃低8
℃
的温度。
2-8=2+(-8)=-6
℃
-3-6=(-3)+(-6)=-9
℃
-392
392
死海
3、如图,世界上最高峰是珠穆朗玛峰,陆上最低处是死海(位于亚洲西部的一个湖泊)求两处高度相差多少?
8848-(-392)
=9240(米)
=8848+(+392)
答:两处高度差为9240米.
4、选择题:
(1)较小的数减去较大的数,所得的数一定是(
)
A
0
B
正数
C
负数
D
0或负数
(2)下列说法正确的是(
)
A
减去一个
负数,差一定大于被减数;
B
减去一个正数,差不一定小于被减数;
C
0
减去任何数,差都是负数;
D
两个数之差一定小于被减数;
C
A
(3)下列说法正确的是(
)
A
减去一个数,等于加上这个数;
B
有理数的减法中,被减数不一定比减数大;
C
0
减去一个数
,仍得
这个数;
D
两个相反数相减得
0
;
(4)差是-5,被减数是-2,则减数为(
)
A
-7
B
-3
C
3
D
-7
B
C
1、有理数减法的意义
2、有理数的减法法则
小结
3、有理数的减法的运算步骤
注意点:
1、被减数与减数的位置不能互换
2、减法法则不能与加法法则中的两个异号的数相加混淆。
3、不存在“不够减”的问题(可用作差法比较两个有理数的大小)
作业:
必做:课本P25第3、4
选作:导学与训练
