矩形的性质教学案
图片预览

文档简介
课题:19.2.1矩形的性质 课型:新授课
一.教学目标
1.情感目标:培养学生自学的学习热情,自主合作的精神,体会逻辑推理的思维价值。
2.能力目标:经历探索矩形的概念和性质的过程,发展学生合情推理的意识;掌握几何思
维方法和综合运用知识解决问题的能力.
3.知识目标:(1)理解矩形的概念,掌握矩形的性质及推论;理解矩形与平行四边形的区
别与联系.
(2)会利用矩形的性质及推论进行有关计算与证明.
二.重点难点
重点:矩形的概念、性质和推论及其应用.
难点:性质2的推论的证明及矩形性质的综合运用.
三.教法与建议
1.用1课时完成教学任务.
2.自学、观察、操作、讨论交流.
四.学法与要求
1.复习平行四边形的有关性质,阅读课本P94——P95,并完成讲学稿.
2.运用类比、联系的学习方法来学习矩形的性质.
五.教学活动程序
【一】知识链接
1.平行四边形的定义:有两组对边___________的四边形叫做平行四边形.
2.平行四边形的性质有:
(1)边:对边____________;
(2)角:对角________;
(3)对角线:对角线_____________.
(4)对称性:是_______对称图形,对称中心是______________.
【二】探究新知
A.矩形的性质
1.生活中一些平行四边形的实际应用图片(推拉门,活动衣架,篱笆、井架等),想一想:这里面应用了平行四边形的什么性质?
2.思考:拿一个活动的平行四边形木架,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗?为什么?
3.当移动到一个角是直角时停止,平行四边形变成什么图形?
矩形定义:有_______________的平行四边形叫做矩形.(也就是______形)
生活中有哪些物体的表面给我们以矩形的形象?_________________________________________________.
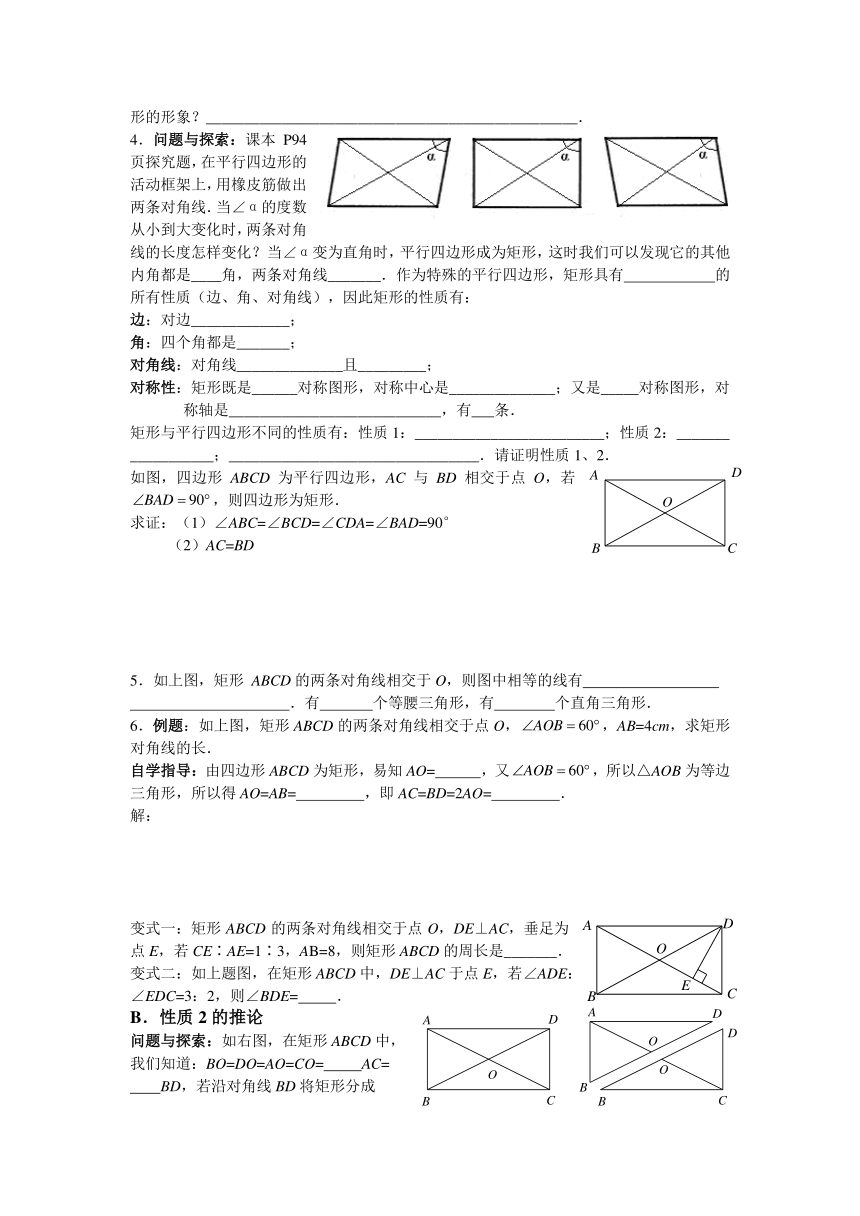
4.问题与探索:课本P94页探究题,在平行四边形的活动框架上,用橡皮筋做出两条对角线.当∠α的度数从小到大变化时,两条对角线的长度怎样变化?当∠α变为直角时,平行四边形成为矩形,这时我们可以发现它的其他内角都是____角,两条对角线_______.作为特殊的平行四边形,矩形具有 的所有性质(边、角、对角线),因此矩形的性质有:
边:对边_____________;
角:四个角都是_______;
对角线:对角线______________且_________;
对称性:矩形既是______对称图形,对称中心是______________;又是_____对称图形,对
称轴是____________________________,有___条.
矩形与平行四边形不同的性质有:性质1:_________________________;性质2:_______
___________;_________________________________.请证明性质1、2.
如图,四边形ABCD为平行四边形,AC与BD相交于点O,若,则四边形为矩形.
求证:(1)∠ABC=∠BCD=∠CDA=∠BAD=90°
(2)AC=BD
5.如上图,矩形 ABCD的两条对角线相交于O,则图中相等的线有
.有 个等腰三角形,有 个直角三角形.
6.例题:如上图,矩形ABCD的两条对角线相交于点O,,AB=4cm,求矩形对角线的长.
自学指导:由四边形ABCD为矩形,易知AO= ,又,所以△AOB为等边三角形,所以得AO=AB= ,即AC=BD=2AO= .
解:
变式一:矩形ABCD的两条对角线相交于点O,DE⊥AC,垂足为点E,若CE∶AE=1∶3,AB=8,则矩形ABCD的周长是_______.
变式二:如上题图,在矩形ABCD中,DE⊥AC于点E,若∠ADE:∠EDC=3:2,则∠BDE= .
B.性质2的推论
问题与探索:如右图,在矩形ABCD中,
我们知道:BO=DO=AO=CO= AC=
BD,若沿对角线BD将矩形分成
Rt△ABD和Rt△CDB,则OA=___BD,OC=___BD.于是我们得到直角三角形的一个重要性质:直角三角形 上的中线等于斜边 .
是不是所有的直角三角形都有这样的性质呢?我们还需要证明.
7.如图,在△ABC中,∠ACB=90°,D为AB的中点.
求证:CD=AB.
分析:刚才我们是通过矩形的性质得到直角三角形的这一性质的,现在要证明这一性质,能不能联系上面两个图,根据矩形的定义作辅助性把三角形放到矩形中来解决呢?
证明:
8.例题:如图,BD、CE是的高,G、F分别是BC、DE的中点,
求证:FG⊥DE
自学指导:有中点,有直角三角形,可构造斜边上的中线,连接EG和DG,则可证EG= ;再由三线合一定理即可得证.
证明:
【三】综合与运用
9.直角三角形中,两条边长分别为3和4,则斜边中线长是 .
10.如图,在矩形ABCD中,点E是BC上一动点,DF⊥AE与F.
(1)若AE=AD,求证:DF=CD.
(2)若AB=3,AD=4,设AE为y,DF为x,求y与x的函数
关系式,并写出自变量x的取值范围,画出函数图像.
11*.如图,矩形ABCD中,AC、BD相交于点,AE平分∠BAD交BC于点E,,若∠CAE=,则下列结论中①△AOB为等边三角形;②∠BOE=;③OE=EC;④AO=BE;⑤OE=OF.
其中正确的有 .(填序号)
12*.如图,矩形ABCD中,AB=3,AD=4,P是AD上一点,
PE⊥AC于E点,PF⊥BD于F点,则PE+PF的值为
.(提示:可利用面积法来求解)
【四】拓展与延伸(选讲.选做)
13*.如图,在△ABC中,∠ACB=90°,点E为AB的中点,连接CE,过点E作ED⊥BC于D,在DE的延长线上取一点F,使AF=CE.
求证:四边形ACEF为平行四边形.
【五】评价与反思
A.自学后评价
学 生 自 评 家 长 评 价
自学效果评价 A.好 B.一般 C.不太理想 自学态度
你有哪些疑惑 完成时间
家长签名
B.学完后评价
1.本节课学会了哪些重要的知识和思想方法?有哪些值得注意或改进的地方?
2.你还有哪些疑惑?
C.教后反思:
F
一.教学目标
1.情感目标:培养学生自学的学习热情,自主合作的精神,体会逻辑推理的思维价值。
2.能力目标:经历探索矩形的概念和性质的过程,发展学生合情推理的意识;掌握几何思
维方法和综合运用知识解决问题的能力.
3.知识目标:(1)理解矩形的概念,掌握矩形的性质及推论;理解矩形与平行四边形的区
别与联系.
(2)会利用矩形的性质及推论进行有关计算与证明.
二.重点难点
重点:矩形的概念、性质和推论及其应用.
难点:性质2的推论的证明及矩形性质的综合运用.
三.教法与建议
1.用1课时完成教学任务.
2.自学、观察、操作、讨论交流.
四.学法与要求
1.复习平行四边形的有关性质,阅读课本P94——P95,并完成讲学稿.
2.运用类比、联系的学习方法来学习矩形的性质.
五.教学活动程序
【一】知识链接
1.平行四边形的定义:有两组对边___________的四边形叫做平行四边形.
2.平行四边形的性质有:
(1)边:对边____________;
(2)角:对角________;
(3)对角线:对角线_____________.
(4)对称性:是_______对称图形,对称中心是______________.
【二】探究新知
A.矩形的性质
1.生活中一些平行四边形的实际应用图片(推拉门,活动衣架,篱笆、井架等),想一想:这里面应用了平行四边形的什么性质?
2.思考:拿一个活动的平行四边形木架,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗?为什么?
3.当移动到一个角是直角时停止,平行四边形变成什么图形?
矩形定义:有_______________的平行四边形叫做矩形.(也就是______形)
生活中有哪些物体的表面给我们以矩形的形象?_________________________________________________.
4.问题与探索:课本P94页探究题,在平行四边形的活动框架上,用橡皮筋做出两条对角线.当∠α的度数从小到大变化时,两条对角线的长度怎样变化?当∠α变为直角时,平行四边形成为矩形,这时我们可以发现它的其他内角都是____角,两条对角线_______.作为特殊的平行四边形,矩形具有 的所有性质(边、角、对角线),因此矩形的性质有:
边:对边_____________;
角:四个角都是_______;
对角线:对角线______________且_________;
对称性:矩形既是______对称图形,对称中心是______________;又是_____对称图形,对
称轴是____________________________,有___条.
矩形与平行四边形不同的性质有:性质1:_________________________;性质2:_______
___________;_________________________________.请证明性质1、2.
如图,四边形ABCD为平行四边形,AC与BD相交于点O,若,则四边形为矩形.
求证:(1)∠ABC=∠BCD=∠CDA=∠BAD=90°
(2)AC=BD
5.如上图,矩形 ABCD的两条对角线相交于O,则图中相等的线有
.有 个等腰三角形,有 个直角三角形.
6.例题:如上图,矩形ABCD的两条对角线相交于点O,,AB=4cm,求矩形对角线的长.
自学指导:由四边形ABCD为矩形,易知AO= ,又,所以△AOB为等边三角形,所以得AO=AB= ,即AC=BD=2AO= .
解:
变式一:矩形ABCD的两条对角线相交于点O,DE⊥AC,垂足为点E,若CE∶AE=1∶3,AB=8,则矩形ABCD的周长是_______.
变式二:如上题图,在矩形ABCD中,DE⊥AC于点E,若∠ADE:∠EDC=3:2,则∠BDE= .
B.性质2的推论
问题与探索:如右图,在矩形ABCD中,
我们知道:BO=DO=AO=CO= AC=
BD,若沿对角线BD将矩形分成
Rt△ABD和Rt△CDB,则OA=___BD,OC=___BD.于是我们得到直角三角形的一个重要性质:直角三角形 上的中线等于斜边 .
是不是所有的直角三角形都有这样的性质呢?我们还需要证明.
7.如图,在△ABC中,∠ACB=90°,D为AB的中点.
求证:CD=AB.
分析:刚才我们是通过矩形的性质得到直角三角形的这一性质的,现在要证明这一性质,能不能联系上面两个图,根据矩形的定义作辅助性把三角形放到矩形中来解决呢?
证明:
8.例题:如图,BD、CE是的高,G、F分别是BC、DE的中点,
求证:FG⊥DE
自学指导:有中点,有直角三角形,可构造斜边上的中线,连接EG和DG,则可证EG= ;再由三线合一定理即可得证.
证明:
【三】综合与运用
9.直角三角形中,两条边长分别为3和4,则斜边中线长是 .
10.如图,在矩形ABCD中,点E是BC上一动点,DF⊥AE与F.
(1)若AE=AD,求证:DF=CD.
(2)若AB=3,AD=4,设AE为y,DF为x,求y与x的函数
关系式,并写出自变量x的取值范围,画出函数图像.
11*.如图,矩形ABCD中,AC、BD相交于点,AE平分∠BAD交BC于点E,,若∠CAE=,则下列结论中①△AOB为等边三角形;②∠BOE=;③OE=EC;④AO=BE;⑤OE=OF.
其中正确的有 .(填序号)
12*.如图,矩形ABCD中,AB=3,AD=4,P是AD上一点,
PE⊥AC于E点,PF⊥BD于F点,则PE+PF的值为
.(提示:可利用面积法来求解)
【四】拓展与延伸(选讲.选做)
13*.如图,在△ABC中,∠ACB=90°,点E为AB的中点,连接CE,过点E作ED⊥BC于D,在DE的延长线上取一点F,使AF=CE.
求证:四边形ACEF为平行四边形.
【五】评价与反思
A.自学后评价
学 生 自 评 家 长 评 价
自学效果评价 A.好 B.一般 C.不太理想 自学态度
你有哪些疑惑 完成时间
家长签名
B.学完后评价
1.本节课学会了哪些重要的知识和思想方法?有哪些值得注意或改进的地方?
2.你还有哪些疑惑?
C.教后反思:
F
