人教版(2019)高一物理必修二第五章5.4.抛体运动的规律课件(共39张PPT)
文档属性
| 名称 | 人教版(2019)高一物理必修二第五章5.4.抛体运动的规律课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-18 07:40:23 | ||
图片预览










文档简介
4 抛体运动的规律
第五章 抛体运动
1.熟练掌握平抛运动的研究方法.
2.会用运动合成和分解的知识分析求解平抛运动的速度和位移,知道平抛运动的轨迹为抛物线.
3.了解斜抛运动及其运动规律,知道运动的合成与分解是分析抛体运动的一般方法.
学习目标
梳理教材 夯实基础
探究重点 提升素养
随堂演练 逐点落实
内容索引
NEIRONGSUOYIN
梳理教材 夯实基础
01
以速度v0沿水平方向抛出一物体,以抛出点为原点,建立如图1所示的平面直角坐标系.
平抛运动的速度
一
图1
(1)水平方向:不受力,加速度是
,水平方向为
运动,vx=
.
(2)竖直方向:只受重力,由牛顿第二定律得到:mg=ma.所以a=
;竖直方向的初速度为
,所以竖直方向为
运动,vy=
.
(3)合速度
0
匀速直线
v0
g
0
自由落体
gt
方向:tan
θ=
=
(θ是v与水平方向的夹角).
1.水平位移:x=
①
2.竖直位移:y=
②
3.轨迹方程:由①②两式消去时间t,可得平抛运动的轨迹方程为y=
,由此可知平抛运动的轨迹是一条
.
平抛运动的位移与轨迹
二
v0t
抛物线
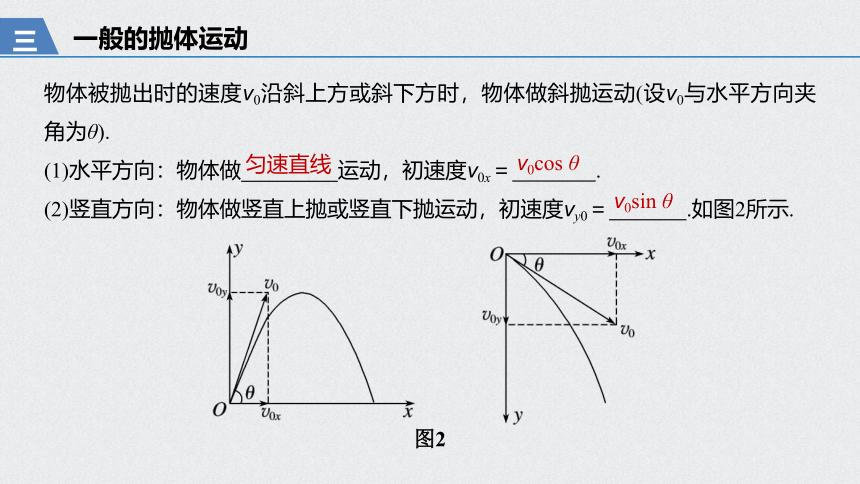
物体被抛出时的速度v0沿斜上方或斜下方时,物体做斜抛运动(设v0与水平方向夹角为θ).
(1)水平方向:物体做
运动,初速度v0x=
.
(2)竖直方向:物体做竖直上抛或竖直下抛运动,初速度vy0=
.如图2所示.
一般的抛体运动
三
匀速直线
v0cos
θ
v0sin
θ
图2
即学即用
1.判断下列说法的正误.
(1)抛体运动一定是匀变速运动.( )
(2)平抛运动的物体初速度越大,下落得越快.( )
(3)平抛运动物体的速度方向与水平方向的夹角越来越大,若足够高,速度方向最终可能竖直向下.( )
(4)平抛运动的合位移的方向与合速度的方向一致.( )
(5)斜上抛运动的物体到达最高点时,速度为零.( )
√
×
×
×
×
2.在距地面高80
m的低空有一小型飞机以30
m/s的速度水平飞行,假定从飞机上释放一物体,g取10
m/s2,不计空气阻力,那么物体落地时间是
s,它在下落过程中发生的水平位移是
m;落地前瞬间的速度大小为
m/s.
4
120
50
水平位移x=v0t,代入数据得:
x=30×4
m=120
m
代入数据得v=50
m/s.
探究重点 提升素养
02
对平抛运动的理解
一
导学探究
图3为一人正在练投掷飞镖,请思考:(不计空气阻力)
(1)飞镖掷出后,其加速度的大小和方向是否变化?
答案 加速度为重力加速度g,大小和方向均不变.
(2)飞镖的运动是什么性质的运动?
答案 匀变速曲线运动.
图3
知识深化
1.平抛运动的特点
(1)做平抛运动的物体水平方向不受力,做匀速直线运动;竖直方向只受重力,做自由落体运动;其合运动为匀变速曲线运动,其轨迹为抛物线.
(2)平抛运动的速度方向沿轨迹的切线方向,速度大小、方向不断变化.
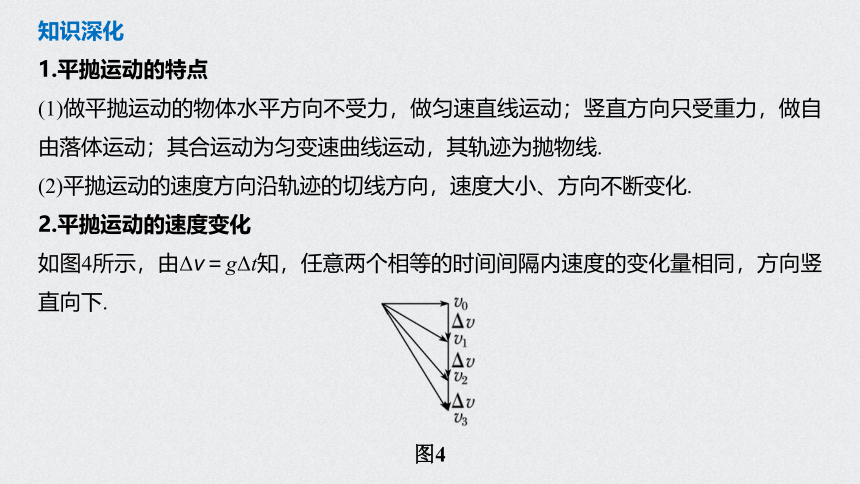
2.平抛运动的速度变化
如图4所示,由Δv=gΔt知,任意两个相等的时间间隔内速度的变化量相同,方向竖直向下.
图4
例1 (2019·蚌埠市第二学期质检)关于平抛运动,下列说法中正确的是
A.平抛运动是一种变加速运动
B.做平抛运动的物体加速度随时间逐渐增大
C.做平抛运动的物体每秒内速度增量相等
D.做平抛运动的物体每秒内位移增量相等
解析 平抛运动是匀变速曲线运动,其加速度为重力加速度g,故加速度的大小和方向恒定,在Δt时间内速度的改变量为Δv=gΔt,因此可知每秒内速度增量大小相等、方向相同,选项A、B错误,C正确;
√
由于水平方向的位移x=v0t,每秒内水平位移增量相等,而竖直方向的位移h=
gt2,每秒内竖直位移增量不相等,故每秒内位移增量不相等,选项D错误.
平抛运动规律的应用
二
导学探究
图5为小球水平抛出后,在空中做平抛运动的运动轨迹.(自由落体加速度为g,初速度为v0,不计空气阻力)
(1)小球做平抛运动,为了便于研究,我们应如何建立坐标系?
图5
答案 一般以初速度v0的方向为x轴的正方向,竖直向下的方向为y轴的正方向,以小球被抛出的位置为坐标原点,建立平面直角坐标系.
(2)以抛出时刻为计时起点,求t时刻小球的速度大小和方向.
(3)以抛出时刻为计时起点,求t时刻小球的位移大小和方向.
答案 如图所示,水平方向:x=v0t
知识深化
1.平抛运动的研究方法
(1)把平抛运动分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动.
(2)分别运用两个分运动的运动规律去求分速度、分位移等,再合成得到平抛运动的速度、位移等.
2.平抛运动的规律
3.平抛运动的推论
(1)做平抛运动的物体在某时刻,其速度方向与水平方向的夹角为θ,位移方向与水平方向的夹角为α,则有tan
θ=2tan
α.
图6
(2)做平抛运动的物体在任意时刻的速度的反向延长线一定通过此时水平位移的中点.
例2 (2019·平顶山市高一下学期期末)如图7所示为某公园的喷水装置,若水从喷水口中水平喷出,忽略空气阻力及水之间的相互作用,下列说法中正确的是
A.喷水口高度一定,喷水速度越大,水从喷出到落入池中
的时间越短
B.喷水口高度一定,喷水速度越大,水喷得越近
C.喷水速度一定,喷水口高度越高,水喷得越近
D.喷水口高度一定,无论喷水速度多大,水从喷出到落入
池中的时间都相等
图7
√
例3 以30
m/s的初速度水平抛出一个物体,经过一段时间后,物体的速度方向与水平方向成30°角,不计空气阻力,g取10
m/s2.求:
(1)此时物体相对于抛出点的水平位移大小和竖直位移大小;
(2)再经过多长时间,物体的速度方向与水平方向的夹角为60°.(物体的抛出点足够高)
平抛运动的临界问题
三
例4 (多选)(2019·定远育才学校第二学期期末)如图8所示,水平屋顶高H=5
m,围墙高h=3.2
m,围墙到房子的水平距离L=3
m,围墙外马路宽x=10
m,为使小球从屋顶水平飞出落在围墙外的马路上,小球离开屋顶时的速度v0的大小的可能值为(围墙厚度忽略不计,忽略空气阻力,g取10
m/s2)
图8
A.6
m/s
B.12
m/s
C.4
m/s
D.2
m/s
√
√
解析 刚好能越过围墙时,水平方向:L=v0t
解得v0=5
m/s
刚好能落到马路外边缘时,水平方向:L+x=v0′t′
解得v0′=13
m/s,
所以为使小球从屋顶水平飞出落在围墙外的马路上,速度的取值5
m/s≤v≤13
m/s,故选A、B.
归纳总结
分析平抛运动中的临界问题时一般运用极限分析的方法,即把要求的物理量设定为极大或极小,让临界问题突显出来,找出满足临界状态的条件.
针对训练 一阶梯如图9所示,其中每级台阶的高度和宽度都是0.4
m,一小球以水平速度v从图示位置飞出,不计空气阻力,g取10
m/s2,欲打在第4级台阶上,则v的取值范围是
图9
√
解析 若恰好打在第3级台阶的边缘,则有:
若恰好打在第4级台阶的边缘,
所以打在第4级台阶上应满足的条件:
斜抛运动
四
1.斜抛运动的规律
(1)斜抛运动的性质:斜抛运动是加速度恒为重力加速度g的匀变速曲线运动,轨迹是抛物线.
(2)斜抛运动的基本规律(以斜上抛为例说明,如图10所示)
①水平方向:v0x=v0cos
θ,F合x=0.
②竖直方向:v0y=v0sin
θ,F合y=mg.
图10
(3)斜上抛运动可以看成水平方向的匀速直线运动和竖直方向的竖直上抛运动的合运动.
①速度公式:vx=v0x=v0cos
θ
vy=v0y-gt=v0sin
θ-gt
②位移公式:x=v0cos
θ·t
2.斜抛运动的对称性
(1)时间对称:相对于轨迹最高点,两侧对称的上升时间等于下降时间.
(2)速度对称:相对于轨迹最高点,两侧对称的两点速度大小相等.
(3)轨迹对称:斜抛运动的轨迹相对于过最高点的竖直线对称.
例5 苏格兰的塞尔海峡位于欧洲大陆与塞尔岛之间,这个海峡宽约6
m,假设有一位运动员,他要以与水平面成37°的角度斜向上进行“越海之跳”,可使这位运动员越过这个海峡的初速度的最小值是多少?(忽略空气阻力.sin
37°=0.6,cos
37°=0.8,g取10
m/s2)
解析 设该运动员的最小初速度为v0,其在水平方向运动的距离恰为6
m,则其水平分速度:v0x=v0cos
37°
水平位移:x=v0xt
竖直分速度:v0y=v0sin
37°
随堂演练 逐点落实
03
1.(平抛运动的理解)(多选)关于平抛运动,下列说法正确的是
A.平抛运动是一种在恒力作用下的曲线运动
B.平抛运动的速度方向与合力方向的夹角保持不变
C.平抛运动的速度大小是时刻变化的
D.平抛运动的速度方向与加速度方向的夹角一定越来越小
解析 做平抛运动的物体只受重力作用,故A正确;
√
1
2
3
4
√
√
2.(平抛运动规律的应用)(多选)(2018·南充市高一检测)如图11所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上,已知底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列表述正确的是
1
2
3
4
图11
√
√
1
2
3
4
3.(平抛运动规律的应用)(2019·永春一中高一下学期期末)如图12所示,喷枪水平放置且固定,图中虚线分别为水平线和竖直线.A、B、C、D为喷枪射出的打在墙上的四个液滴,四个液滴均可以视为质点;不计空气阻力,已知D、C、B、A与水平线的间距依次为1
cm、4
cm、9
cm、16
cm,则下列说法正确的是
A.A、B、C、D四个液滴的射出速度相同
B.A、B、C、D四个液滴在空中的运动时间是相同的
C.A、B、C、D四个液滴出射速度之比应为1∶2∶3∶4
D.A、B、C、D四个液滴出射速度之比应为3∶4∶6∶12
1
2
3
4
图12
√
1
2
3
4
4.(平抛运动的临界问题)如图13所示,M、N是两块挡板,挡板M高h′=10
m,其上边缘与挡板N的下边缘在同一水平面.从高h=15
m的A点以速度v0水平抛出一小球(可视为质点),A点与两挡板的水平距离分别为d1=10
m,d2=20
m.N板的上边缘高于A点,若能使小球直接进入挡板M的右边区域,则小球水平抛出的初速度v0的大小可能是下列给出数据中的哪个(g取10
m/s2,空气阻力不计)
A.8
m/s
B.4
m/s
C.15
m/s
D.21
m/s
1
2
3
4
图13
√
1
2
3
4
第五章 抛体运动
1.熟练掌握平抛运动的研究方法.
2.会用运动合成和分解的知识分析求解平抛运动的速度和位移,知道平抛运动的轨迹为抛物线.
3.了解斜抛运动及其运动规律,知道运动的合成与分解是分析抛体运动的一般方法.
学习目标
梳理教材 夯实基础
探究重点 提升素养
随堂演练 逐点落实
内容索引
NEIRONGSUOYIN
梳理教材 夯实基础
01
以速度v0沿水平方向抛出一物体,以抛出点为原点,建立如图1所示的平面直角坐标系.
平抛运动的速度
一
图1
(1)水平方向:不受力,加速度是
,水平方向为
运动,vx=
.
(2)竖直方向:只受重力,由牛顿第二定律得到:mg=ma.所以a=
;竖直方向的初速度为
,所以竖直方向为
运动,vy=
.
(3)合速度
0
匀速直线
v0
g
0
自由落体
gt
方向:tan
θ=
=
(θ是v与水平方向的夹角).
1.水平位移:x=
①
2.竖直位移:y=
②
3.轨迹方程:由①②两式消去时间t,可得平抛运动的轨迹方程为y=
,由此可知平抛运动的轨迹是一条
.
平抛运动的位移与轨迹
二
v0t
抛物线
物体被抛出时的速度v0沿斜上方或斜下方时,物体做斜抛运动(设v0与水平方向夹角为θ).
(1)水平方向:物体做
运动,初速度v0x=
.
(2)竖直方向:物体做竖直上抛或竖直下抛运动,初速度vy0=
.如图2所示.
一般的抛体运动
三
匀速直线
v0cos
θ
v0sin
θ
图2
即学即用
1.判断下列说法的正误.
(1)抛体运动一定是匀变速运动.( )
(2)平抛运动的物体初速度越大,下落得越快.( )
(3)平抛运动物体的速度方向与水平方向的夹角越来越大,若足够高,速度方向最终可能竖直向下.( )
(4)平抛运动的合位移的方向与合速度的方向一致.( )
(5)斜上抛运动的物体到达最高点时,速度为零.( )
√
×
×
×
×
2.在距地面高80
m的低空有一小型飞机以30
m/s的速度水平飞行,假定从飞机上释放一物体,g取10
m/s2,不计空气阻力,那么物体落地时间是
s,它在下落过程中发生的水平位移是
m;落地前瞬间的速度大小为
m/s.
4
120
50
水平位移x=v0t,代入数据得:
x=30×4
m=120
m
代入数据得v=50
m/s.
探究重点 提升素养
02
对平抛运动的理解
一
导学探究
图3为一人正在练投掷飞镖,请思考:(不计空气阻力)
(1)飞镖掷出后,其加速度的大小和方向是否变化?
答案 加速度为重力加速度g,大小和方向均不变.
(2)飞镖的运动是什么性质的运动?
答案 匀变速曲线运动.
图3
知识深化
1.平抛运动的特点
(1)做平抛运动的物体水平方向不受力,做匀速直线运动;竖直方向只受重力,做自由落体运动;其合运动为匀变速曲线运动,其轨迹为抛物线.
(2)平抛运动的速度方向沿轨迹的切线方向,速度大小、方向不断变化.
2.平抛运动的速度变化
如图4所示,由Δv=gΔt知,任意两个相等的时间间隔内速度的变化量相同,方向竖直向下.
图4
例1 (2019·蚌埠市第二学期质检)关于平抛运动,下列说法中正确的是
A.平抛运动是一种变加速运动
B.做平抛运动的物体加速度随时间逐渐增大
C.做平抛运动的物体每秒内速度增量相等
D.做平抛运动的物体每秒内位移增量相等
解析 平抛运动是匀变速曲线运动,其加速度为重力加速度g,故加速度的大小和方向恒定,在Δt时间内速度的改变量为Δv=gΔt,因此可知每秒内速度增量大小相等、方向相同,选项A、B错误,C正确;
√
由于水平方向的位移x=v0t,每秒内水平位移增量相等,而竖直方向的位移h=
gt2,每秒内竖直位移增量不相等,故每秒内位移增量不相等,选项D错误.
平抛运动规律的应用
二
导学探究
图5为小球水平抛出后,在空中做平抛运动的运动轨迹.(自由落体加速度为g,初速度为v0,不计空气阻力)
(1)小球做平抛运动,为了便于研究,我们应如何建立坐标系?
图5
答案 一般以初速度v0的方向为x轴的正方向,竖直向下的方向为y轴的正方向,以小球被抛出的位置为坐标原点,建立平面直角坐标系.
(2)以抛出时刻为计时起点,求t时刻小球的速度大小和方向.
(3)以抛出时刻为计时起点,求t时刻小球的位移大小和方向.
答案 如图所示,水平方向:x=v0t
知识深化
1.平抛运动的研究方法
(1)把平抛运动分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动.
(2)分别运用两个分运动的运动规律去求分速度、分位移等,再合成得到平抛运动的速度、位移等.
2.平抛运动的规律
3.平抛运动的推论
(1)做平抛运动的物体在某时刻,其速度方向与水平方向的夹角为θ,位移方向与水平方向的夹角为α,则有tan
θ=2tan
α.
图6
(2)做平抛运动的物体在任意时刻的速度的反向延长线一定通过此时水平位移的中点.
例2 (2019·平顶山市高一下学期期末)如图7所示为某公园的喷水装置,若水从喷水口中水平喷出,忽略空气阻力及水之间的相互作用,下列说法中正确的是
A.喷水口高度一定,喷水速度越大,水从喷出到落入池中
的时间越短
B.喷水口高度一定,喷水速度越大,水喷得越近
C.喷水速度一定,喷水口高度越高,水喷得越近
D.喷水口高度一定,无论喷水速度多大,水从喷出到落入
池中的时间都相等
图7
√
例3 以30
m/s的初速度水平抛出一个物体,经过一段时间后,物体的速度方向与水平方向成30°角,不计空气阻力,g取10
m/s2.求:
(1)此时物体相对于抛出点的水平位移大小和竖直位移大小;
(2)再经过多长时间,物体的速度方向与水平方向的夹角为60°.(物体的抛出点足够高)
平抛运动的临界问题
三
例4 (多选)(2019·定远育才学校第二学期期末)如图8所示,水平屋顶高H=5
m,围墙高h=3.2
m,围墙到房子的水平距离L=3
m,围墙外马路宽x=10
m,为使小球从屋顶水平飞出落在围墙外的马路上,小球离开屋顶时的速度v0的大小的可能值为(围墙厚度忽略不计,忽略空气阻力,g取10
m/s2)
图8
A.6
m/s
B.12
m/s
C.4
m/s
D.2
m/s
√
√
解析 刚好能越过围墙时,水平方向:L=v0t
解得v0=5
m/s
刚好能落到马路外边缘时,水平方向:L+x=v0′t′
解得v0′=13
m/s,
所以为使小球从屋顶水平飞出落在围墙外的马路上,速度的取值5
m/s≤v≤13
m/s,故选A、B.
归纳总结
分析平抛运动中的临界问题时一般运用极限分析的方法,即把要求的物理量设定为极大或极小,让临界问题突显出来,找出满足临界状态的条件.
针对训练 一阶梯如图9所示,其中每级台阶的高度和宽度都是0.4
m,一小球以水平速度v从图示位置飞出,不计空气阻力,g取10
m/s2,欲打在第4级台阶上,则v的取值范围是
图9
√
解析 若恰好打在第3级台阶的边缘,则有:
若恰好打在第4级台阶的边缘,
所以打在第4级台阶上应满足的条件:
斜抛运动
四
1.斜抛运动的规律
(1)斜抛运动的性质:斜抛运动是加速度恒为重力加速度g的匀变速曲线运动,轨迹是抛物线.
(2)斜抛运动的基本规律(以斜上抛为例说明,如图10所示)
①水平方向:v0x=v0cos
θ,F合x=0.
②竖直方向:v0y=v0sin
θ,F合y=mg.
图10
(3)斜上抛运动可以看成水平方向的匀速直线运动和竖直方向的竖直上抛运动的合运动.
①速度公式:vx=v0x=v0cos
θ
vy=v0y-gt=v0sin
θ-gt
②位移公式:x=v0cos
θ·t
2.斜抛运动的对称性
(1)时间对称:相对于轨迹最高点,两侧对称的上升时间等于下降时间.
(2)速度对称:相对于轨迹最高点,两侧对称的两点速度大小相等.
(3)轨迹对称:斜抛运动的轨迹相对于过最高点的竖直线对称.
例5 苏格兰的塞尔海峡位于欧洲大陆与塞尔岛之间,这个海峡宽约6
m,假设有一位运动员,他要以与水平面成37°的角度斜向上进行“越海之跳”,可使这位运动员越过这个海峡的初速度的最小值是多少?(忽略空气阻力.sin
37°=0.6,cos
37°=0.8,g取10
m/s2)
解析 设该运动员的最小初速度为v0,其在水平方向运动的距离恰为6
m,则其水平分速度:v0x=v0cos
37°
水平位移:x=v0xt
竖直分速度:v0y=v0sin
37°
随堂演练 逐点落实
03
1.(平抛运动的理解)(多选)关于平抛运动,下列说法正确的是
A.平抛运动是一种在恒力作用下的曲线运动
B.平抛运动的速度方向与合力方向的夹角保持不变
C.平抛运动的速度大小是时刻变化的
D.平抛运动的速度方向与加速度方向的夹角一定越来越小
解析 做平抛运动的物体只受重力作用,故A正确;
√
1
2
3
4
√
√
2.(平抛运动规律的应用)(多选)(2018·南充市高一检测)如图11所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以速度v沿垂直球网的方向击出,球刚好落在底线上,已知底线到网的距离为L,重力加速度为g,将球的运动视作平抛运动,下列表述正确的是
1
2
3
4
图11
√
√
1
2
3
4
3.(平抛运动规律的应用)(2019·永春一中高一下学期期末)如图12所示,喷枪水平放置且固定,图中虚线分别为水平线和竖直线.A、B、C、D为喷枪射出的打在墙上的四个液滴,四个液滴均可以视为质点;不计空气阻力,已知D、C、B、A与水平线的间距依次为1
cm、4
cm、9
cm、16
cm,则下列说法正确的是
A.A、B、C、D四个液滴的射出速度相同
B.A、B、C、D四个液滴在空中的运动时间是相同的
C.A、B、C、D四个液滴出射速度之比应为1∶2∶3∶4
D.A、B、C、D四个液滴出射速度之比应为3∶4∶6∶12
1
2
3
4
图12
√
1
2
3
4
4.(平抛运动的临界问题)如图13所示,M、N是两块挡板,挡板M高h′=10
m,其上边缘与挡板N的下边缘在同一水平面.从高h=15
m的A点以速度v0水平抛出一小球(可视为质点),A点与两挡板的水平距离分别为d1=10
m,d2=20
m.N板的上边缘高于A点,若能使小球直接进入挡板M的右边区域,则小球水平抛出的初速度v0的大小可能是下列给出数据中的哪个(g取10
m/s2,空气阻力不计)
A.8
m/s
B.4
m/s
C.15
m/s
D.21
m/s
1
2
3
4
图13
√
1
2
3
4
