1.4.1 有理数的乘法(1)课件(26张PPT)
文档属性
| 名称 | 1.4.1 有理数的乘法(1)课件(26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 09:51:28 | ||
图片预览








文档简介
第 一 章 有理数
1.4 有理数的乘除法
1.4.1 有理数的乘法
课时1 有理数的乘法法则
2020年秋人教版数学七年级上册精品课件
1.理解有理数的乘法法则.(重点)
2.能熟练进行有理数的乘法运算.(重点)
3.理解有理数的倒数的意义,会求一个有理数的倒数.
学习目标
新课导入
解:3×2 = 6
计算
0 ×5 = 0
×
3×2
0
×
5
×
=
思考
我们已经熟悉正数及0的乘法运算,引入负数以后,如何进行有理数的乘法运算呢?
3 ×(-2) = ?
(-3 )×(-2) = ?
新课讲解
知识点1 有理数的乘法法则
合作探究
观察下面的乘法算式,你能发现什么规律?
3×3=9;3×2=6;3×1=3:3×0=0.
思考
1.四个算式有什么共同点?
2.其他两个数有什么变化规律?
左边都有一个乘数3
规律:随着后一个乘数逐次递减1,积逐次递 减3
新课讲解
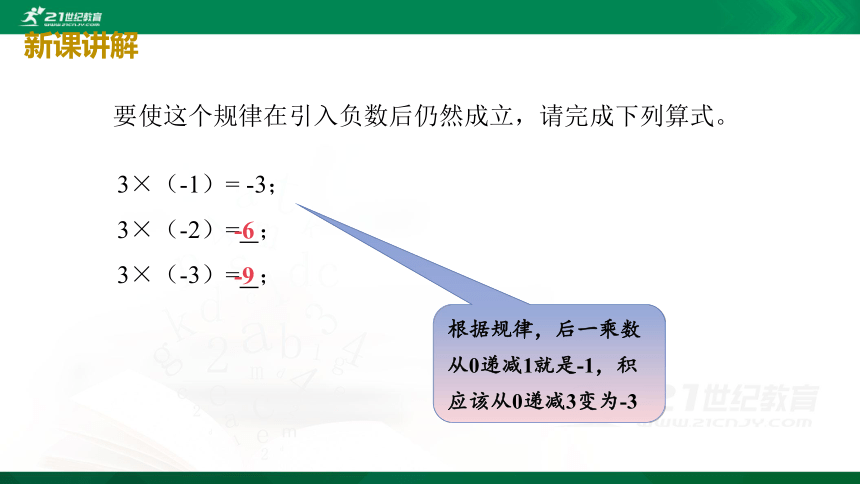
要使这个规律在引入负数后仍然成立,请完成下列算式。
3×(-1)= -3;
3×(-2)= ;
3×(-3)= ;
-6
-9
根据规律,后一乘数从0递减1就是-1,积应该从0递减3变为-3
新课讲解
观察下面的乘法算式,你又能发现什么规律?
3×3=9;2×3=6;1×3=3;0×3=0.
类比上一过程,我们可以得出下面规律:
随着前一个乘数逐次递减1,积逐次递减3
结论
新课讲解
要使这个规律在引入负数后仍然成立,请完成下列算式
(-1)×3= ;
(-2)×3= ;
(-3)×3= ;
3×3=9;
3×2=6;
3×1=3;
3×0=0.
3×(-1)=-3;
3×(-2)=-6;
3×(-3)=-9;
3×3=9;
2×3=6;
1×3=3;
0×3=0.
-3
-6
-9
从符号和绝对值两个角度观察这四组算式,你能得出什么结论?
正数乘正数,积为正数;
正数乘负数,积是负数;
负数乘正数,积也是负数。
积的绝对值等于各乘数绝对值的积。
0乘正数或负数,积都是0
新课讲解
根据上面得出的结论计算下面的算式,你发现有什么规律?
(-3)×3= ;(-3)×2= ;
(-3)×1= ;(-3)×0= .
规律:随着后一个乘数逐次递减1,积逐次增加3
-9
-6
-3
0
结论
新课讲解
根据上面得出的规律计算下面的算式,你从中可以归纳出什么结论?
(-3)×(-1)= ;
(-3)×(-2)= ;
(-3)×(-3)= ;
结论:
负数乘负数,积为正数,乘积的绝对值等于各乘数绝对值的积.
结论
3
6
9
新课讲解
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘,都得0.
结论
新课讲解
例
典例分析
(1)(-5) ×(-3)
(2) (-7)×4
1. 计算
新课讲解
典例分析
(同号两数相乘)
(-5)×(-3)= +( )
(得正)
5×3=15
(把绝对值相乘)
∴(-5)×(-3)=15
(异号两数相乘)
(-7)×4= -( )
(得负)
7×4=28
(把绝对值相乘)
∴(-7)×4=-28
解:
(1)(-5) ×(-3)
(2) (-7)×4
新课讲解
(1)3×4 ; (2) (?3)×9 ;
(3)8 ×(-1); (4)(-3)×(-4)
计算
练一练
新课讲解
解: (1) 3×4 (2) (?3)×9
= +(3×4) = ?(3×9)
= 12 . = ? 27.
(3) 8×(-1) (4)(-3)×(-4)
= 12.
= ?(8 ×1) = +(3×4)
= ?8.
有理数乘法的求解步骤:先确定积的符号,再求两个乘数绝对值的积
练一练
新课讲解
知识点2 倒数
计算:
观察两式有什么特点?
乘积是1的两个数互为倒数.
的倒数是什么?
(1)
; (2)
新课讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
表示方法
符号
性质
特殊数0
倒数
相反数
互为倒数与互为相反数的区别:
相同
积为1
没有倒数
a +(-a)=0
相异
和为0
相反数是自己
课堂小结
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
2.有理数乘法的步骤:
两个有理数相乘,先确定积的符号,再确定积的绝对值.
当堂小练
被乘数
乘数
积的符号
积的绝对值
结果
-4
7
9
6
-3
-6
4
-25
1.填表:
28
-28
54
54
18
18
-100
-
+
+
-
100
当堂小练
2.计算3×(-2)?的结果是( )
(A)5 (B)-5 (C)6 (D)-6
3.如果ab<0,那么下列判断正确的是( )
(A)a<0,b<0 (B)a>0,b>0
(C)a≥0,b≤0 (D)a<0,b>0或a>0,b<0
D
D
【分析】同号得正,异号得负.
当堂小练
4 计算:
当堂小练
解:
当堂小练
5.若a、b互为相反数,若x、y互为倒数,则a-xy +b= .
6.相反数等于它本身的数是 ;倒数等于它本身的数是 ;绝对值等于它本身的数是 .
-1
0
1,-1
非负数
D
拓展与延伸
4.计算:
联系这类具体的数的乘法,你认为一个非0有理数一定小于它的2倍吗?为什么?
解:
不一定,一个负数大于它的2倍.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.4 有理数的乘除法
1.4.1 有理数的乘法
课时1 有理数的乘法法则
2020年秋人教版数学七年级上册精品课件
1.理解有理数的乘法法则.(重点)
2.能熟练进行有理数的乘法运算.(重点)
3.理解有理数的倒数的意义,会求一个有理数的倒数.
学习目标
新课导入
解:3×2 = 6
计算
0 ×5 = 0
×
3×2
0
×
5
×
=
思考
我们已经熟悉正数及0的乘法运算,引入负数以后,如何进行有理数的乘法运算呢?
3 ×(-2) = ?
(-3 )×(-2) = ?
新课讲解
知识点1 有理数的乘法法则
合作探究
观察下面的乘法算式,你能发现什么规律?
3×3=9;3×2=6;3×1=3:3×0=0.
思考
1.四个算式有什么共同点?
2.其他两个数有什么变化规律?
左边都有一个乘数3
规律:随着后一个乘数逐次递减1,积逐次递 减3
新课讲解
要使这个规律在引入负数后仍然成立,请完成下列算式。
3×(-1)= -3;
3×(-2)= ;
3×(-3)= ;
-6
-9
根据规律,后一乘数从0递减1就是-1,积应该从0递减3变为-3
新课讲解
观察下面的乘法算式,你又能发现什么规律?
3×3=9;2×3=6;1×3=3;0×3=0.
类比上一过程,我们可以得出下面规律:
随着前一个乘数逐次递减1,积逐次递减3
结论
新课讲解
要使这个规律在引入负数后仍然成立,请完成下列算式
(-1)×3= ;
(-2)×3= ;
(-3)×3= ;
3×3=9;
3×2=6;
3×1=3;
3×0=0.
3×(-1)=-3;
3×(-2)=-6;
3×(-3)=-9;
3×3=9;
2×3=6;
1×3=3;
0×3=0.
-3
-6
-9
从符号和绝对值两个角度观察这四组算式,你能得出什么结论?
正数乘正数,积为正数;
正数乘负数,积是负数;
负数乘正数,积也是负数。
积的绝对值等于各乘数绝对值的积。
0乘正数或负数,积都是0
新课讲解
根据上面得出的结论计算下面的算式,你发现有什么规律?
(-3)×3= ;(-3)×2= ;
(-3)×1= ;(-3)×0= .
规律:随着后一个乘数逐次递减1,积逐次增加3
-9
-6
-3
0
结论
新课讲解
根据上面得出的规律计算下面的算式,你从中可以归纳出什么结论?
(-3)×(-1)= ;
(-3)×(-2)= ;
(-3)×(-3)= ;
结论:
负数乘负数,积为正数,乘积的绝对值等于各乘数绝对值的积.
结论
3
6
9
新课讲解
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘,都得0.
结论
新课讲解
例
典例分析
(1)(-5) ×(-3)
(2) (-7)×4
1. 计算
新课讲解
典例分析
(同号两数相乘)
(-5)×(-3)= +( )
(得正)
5×3=15
(把绝对值相乘)
∴(-5)×(-3)=15
(异号两数相乘)
(-7)×4= -( )
(得负)
7×4=28
(把绝对值相乘)
∴(-7)×4=-28
解:
(1)(-5) ×(-3)
(2) (-7)×4
新课讲解
(1)3×4 ; (2) (?3)×9 ;
(3)8 ×(-1); (4)(-3)×(-4)
计算
练一练
新课讲解
解: (1) 3×4 (2) (?3)×9
= +(3×4) = ?(3×9)
= 12 . = ? 27.
(3) 8×(-1) (4)(-3)×(-4)
= 12.
= ?(8 ×1) = +(3×4)
= ?8.
有理数乘法的求解步骤:先确定积的符号,再求两个乘数绝对值的积
练一练
新课讲解
知识点2 倒数
计算:
观察两式有什么特点?
乘积是1的两个数互为倒数.
的倒数是什么?
(1)
; (2)
新课讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
表示方法
符号
性质
特殊数0
倒数
相反数
互为倒数与互为相反数的区别:
相同
积为1
没有倒数
a +(-a)=0
相异
和为0
相反数是自己
课堂小结
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
2.有理数乘法的步骤:
两个有理数相乘,先确定积的符号,再确定积的绝对值.
当堂小练
被乘数
乘数
积的符号
积的绝对值
结果
-4
7
9
6
-3
-6
4
-25
1.填表:
28
-28
54
54
18
18
-100
-
+
+
-
100
当堂小练
2.计算3×(-2)?的结果是( )
(A)5 (B)-5 (C)6 (D)-6
3.如果ab<0,那么下列判断正确的是( )
(A)a<0,b<0 (B)a>0,b>0
(C)a≥0,b≤0 (D)a<0,b>0或a>0,b<0
D
D
【分析】同号得正,异号得负.
当堂小练
4 计算:
当堂小练
解:
当堂小练
5.若a、b互为相反数,若x、y互为倒数,则a-xy +b= .
6.相反数等于它本身的数是 ;倒数等于它本身的数是 ;绝对值等于它本身的数是 .
-1
0
1,-1
非负数
D
拓展与延伸
4.计算:
联系这类具体的数的乘法,你认为一个非0有理数一定小于它的2倍吗?为什么?
解:
不一定,一个负数大于它的2倍.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
