北师版数学七年级上册 第四章 基本平面图形 单元测试题(word版,含答案)
文档属性
| 名称 | 北师版数学七年级上册 第四章 基本平面图形 单元测试题(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 299.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 14:55:46 | ||
图片预览




文档简介
北师版数学七年级上册第四章基本平面图形单元测试题.
一、选择题(每题3分,共12题,满分36分)
1.线段具有,射线不具有的性质是
(
)
A.可以延长
B.有无数个点组成
C.可以度量长度
D.可伸长为直线
2.
(2019?海淀区一模)如图1是圆规示意图,张开的两脚所形成的角大约是( )
A.90°
B.60°
C.45°
D.30°
3.
把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是( )
A.两点确定一条直线
B.垂线段最短
C.两点之间线段最短
D.三角形两边之和大于第三边
4.
(2020?德州)如图2,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为( )
A.80米
B.96米
C.64米
D.48米
5.
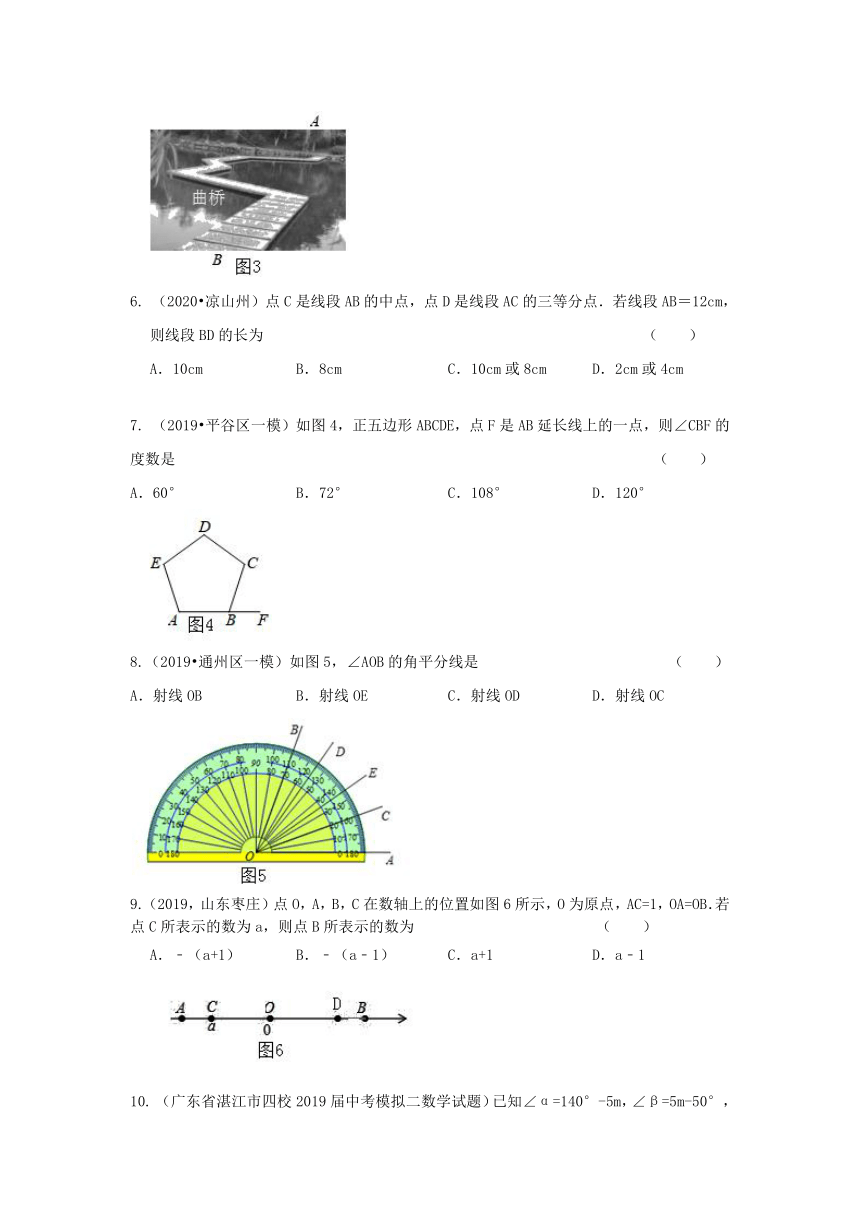
(2019吉林)曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图3,A、B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是
(
)
A.两点之间,线段最短
B.平行于同一条直线的两条直线平行
C.垂线段最短
D.两点确定一条直线
6.
(2020?凉山州)点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12cm,则线段BD的长为
( )
A.10cm
B.8cm
C.10cm或8cm
D.2cm或4cm
7.
(2019?平谷区一模)如图4,正五边形ABCDE,点F是AB延长线上的一点,则∠CBF的度数是
( )
A.60°
B.72°
C.108°
D.120°
8.(2019?通州区一模)如图5,∠AOB的角平分线是
( )
A.射线OB
B.射线OE
C.射线OD
D.射线OC
9.(2019,山东枣庄)点O,A,B,C在数轴上的位置如图6所示,O为原点,AC=1,OA=OB.若点C所表示的数为a,则点B所表示的数为
( )
A.﹣(a+1)
B.﹣(a﹣1)
C.a+1
D.a﹣1
10.
(广东省湛江市四校2019届中考模拟二数学试题)已知∠α=140°-5m,∠β=5m-50°,∠α和∠β关系一定成立的是
(
)
A.∠α+∠β=90°
B.∠α+∠β=190°
C.∠α=∠β
D.∠α=2∠β
11.
(2019·贵州贵阳)数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中
点,则a的值是
(
)
A.3
B.4.5
C.6
D.18
12.(2019淄博)如图7,小明从A处沿北偏东40°方向行走至点B处,又从点B处沿东偏南20°方向行走至点C处,则∠ABC等于
(
)
A.130°
B.120°
C.110°
D.100°
二、填空题(每题2分,共7题,满分14分)
13.如图8,建筑工人砌墙时,经常先在两端立装拉线,然后沿着线砌墙,这里面的数学道理是
.
14.
(2019年广东省佛山市顺德区中考数学三模试卷)计算:18°30′=__________°.
15.已知线段AB=3a,CD=5a,
EF=8a,MN=2a,则AB,CD,EF之间的关系为
,
AB,CD,MN之间的关系为
.
16.(2019?浙江湖州改编)已知∠α=60°32′,则90°﹣∠α为
.
17.
已知直线AB,点C是直线AB上一点,已知线段AB=10cm,线段BC=6cm.则线段AC的长为
.
18.(2019?通州区一模)如图9所示,在一条笔直公路的两侧,分别有A、B两个小区,为了方便居民出行,现要在公路上建一个公共自行车存放点,使存放点到A、B小区的距离之和最小,你认为存放点应该建在 处(填“C”“E”或“D”),理由是
.
19.已知∠AOC=64°,∠BOC=34°.则∠AOB的度数为
.
三、解答题(共8题,满分50分)
20.(满分9分)完成下表:
21.(满分4分)如图10,已知:同一平面内的三点A,B,C,按要求画图:
画线段AB;(2)画射线AC;(3)画直线BC.
22.
(满分4分)(2019年聊城)如图11,数轴上O,A两点的距离为4,一动点P从点A
出发,按以下规律跳动:第1次跳动到AO的中点处,第2次从点跳动到O的中点
处,第3次从点跳动到O的中点处,按照这样的规律继续跳动到点,,,…,
.(n≥3,n是整数)处,求线段A的长(n≥3,n是整数).
23.(满分7分)教材阅读与思考
下面是人教版七年级上册p127页上一段话,请仔细阅读,完成后面的问题:
如图4.2-11(1),点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点.类似地,还有线段的三等分点、四等分点等(图4.2-11(2)(3)),
(1)下列四种说法:①因为AM=MB,所以M是AB中点;②在线段AM的延长线上取一点B,如果AB=2AM,那么M是AB的中点;③因为M是AB的中点,所以AM=MB=AB;④因为A、M、B在同一条直线上,且AM=BM,所以M是AB中点,其中正确的是
(
)
A.①③④
B.④
C.
②③④
D.③④
(2)将一条线段分成相等线段的点叫线段的中点.这句话对吗?为什么?
(3)下列说法正确的是
( )
A、到线段两个端点距离相等的点叫做线段的中点
B、线段的中点到线段两个端点的距离相等
C、线段的中点可以有两个
D、线段的中点有若干个
(4)将一条绳子的两个绳头重合,折痕与绳子的交点,就是绳子的
.
24.
(满分6分如图12,把一个圆分成三个扇形,求出这三个扇形的圆心角.
25.
(满分6分在一条直线上任意取一点A,截取
AB=12cm,再截取AC=38cm,
点D是AB的中点,点E是AC的中点,求:D,E之间的距离.
26.
(满分6分
已知∠AOC=120°∠BOC=20°,OD是∠AOB的平分线,
OE是∠BOC
的平分线,求∠DOE的度数.
27.
(满分6分(2018?高邑县一模)如图13,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是 .
(2)经过几秒,点M、点N分别到原点O的距离相等?
参考答案:
一、选择题
1.C
2.
B
3.
C
4.
C
5.
A
6.
C
7.
B
8.B
9.B
10.
A
11.
C
12.C
二、填空题
13.两点确定一条直线.
14.
18.5
15.
EF=AB+CD;MN=CD-AB.
16.
29°28′
17.
16cm或4cm.
18.
E,两点之间线段最短.
19.
98°或30°.
三、解答题
20.解:
21.解:画图如下:
22.
解:由于OA=4,所有第一次跳动到OA的中点处时,O=OA,同理第二次从点跳动到处,离原点的距离为
O=OA,同理跳动n次后,离原点的距离:OA,所以A=OA-OA=4(1-)(n≥3,n是整数).
23.
解:(1)C
(2)
错误,没有指出是两条相等的线段;(3)B;(4)中点.
24.
解:三个扇形的圆心角分别为:360°×=108°;360°×=72°;360°×=180°.
25.
解:AB与AC重合的端点是点A,当点B,C在点A的同侧时,如图1所示,
因为点D是AB的中点,所以AD=BD=AB;因为点E是AC的中点,所以AE=AC,
因为DE=AE-AD,所以DE=AC-AB=
(AC-AB),
因为AB=12,AC=38,所以DE=
(38-12)=13(cm);
当点B,C在点A的异侧时,如图2所示,
因为点D是AB的中点,所以AD=BD=AB;因为点E是AC的中点,所以AE=AC,
因为DE=AE+AD,所以DE=AC+AB=
(AC+AB),
因为AB=12,AC=38,所以DE=38+12)=25(cm);所以线段DE的长为13cm或25cm.
26.
解:当∠BOC在∠AOC的外部时,如图1,因为OD是∠AOB的平分线,
OE是∠BOC
的平分线,所以∠BOD=∠AOB,∠EOB
=∠BOC,因为∠DOE=∠BOD-∠EOB,
所以∠DOE=∠AOB-∠BOC=
(∠AOB-∠BOC)=
(140°-20°)=60°;
当∠BOC在∠AOC的内部时,如图2,因为OD是∠AOB的平分线,
OE是∠BOC
的平分线,所以∠BOD=∠AOB,∠EOB
=∠BOC,因为∠DOE=∠BOD+∠EOB,
所以∠DOE=∠AOB+∠BOC=
(∠AOB+∠BOC)=
(100°+20°)=60°;
所以∠DOE的度数为60°.
27.
解:(1)因为点A表示的数为﹣10,所以OA=10;因为OB=3OA=30,所以B对应的数是30.
(2)设经过x秒,点M、点N分别到原点O的距离相等,此时点M对应的数为3x﹣10,点N对应的数为2x.
①点M、点N在点O两侧,则3x-10+2x=0,解得x=2;②点M、点N重合,则3x﹣10=2x,
解得x=10.所以经过2秒或10秒,点M、点N分别到原点O的距离相等.
参考答案:
一、选择题(每题3分,共12题,满分36分)
1.线段具有,射线不具有的性质是
(
)
A.可以延长
B.有无数个点组成
C.可以度量长度
D.可伸长为直线
2.
(2019?海淀区一模)如图1是圆规示意图,张开的两脚所形成的角大约是( )
A.90°
B.60°
C.45°
D.30°
3.
把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是( )
A.两点确定一条直线
B.垂线段最短
C.两点之间线段最短
D.三角形两边之和大于第三边
4.
(2020?德州)如图2,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为( )
A.80米
B.96米
C.64米
D.48米
5.
(2019吉林)曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图3,A、B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是
(
)
A.两点之间,线段最短
B.平行于同一条直线的两条直线平行
C.垂线段最短
D.两点确定一条直线
6.
(2020?凉山州)点C是线段AB的中点,点D是线段AC的三等分点.若线段AB=12cm,则线段BD的长为
( )
A.10cm
B.8cm
C.10cm或8cm
D.2cm或4cm
7.
(2019?平谷区一模)如图4,正五边形ABCDE,点F是AB延长线上的一点,则∠CBF的度数是
( )
A.60°
B.72°
C.108°
D.120°
8.(2019?通州区一模)如图5,∠AOB的角平分线是
( )
A.射线OB
B.射线OE
C.射线OD
D.射线OC
9.(2019,山东枣庄)点O,A,B,C在数轴上的位置如图6所示,O为原点,AC=1,OA=OB.若点C所表示的数为a,则点B所表示的数为
( )
A.﹣(a+1)
B.﹣(a﹣1)
C.a+1
D.a﹣1
10.
(广东省湛江市四校2019届中考模拟二数学试题)已知∠α=140°-5m,∠β=5m-50°,∠α和∠β关系一定成立的是
(
)
A.∠α+∠β=90°
B.∠α+∠β=190°
C.∠α=∠β
D.∠α=2∠β
11.
(2019·贵州贵阳)数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中
点,则a的值是
(
)
A.3
B.4.5
C.6
D.18
12.(2019淄博)如图7,小明从A处沿北偏东40°方向行走至点B处,又从点B处沿东偏南20°方向行走至点C处,则∠ABC等于
(
)
A.130°
B.120°
C.110°
D.100°
二、填空题(每题2分,共7题,满分14分)
13.如图8,建筑工人砌墙时,经常先在两端立装拉线,然后沿着线砌墙,这里面的数学道理是
.
14.
(2019年广东省佛山市顺德区中考数学三模试卷)计算:18°30′=__________°.
15.已知线段AB=3a,CD=5a,
EF=8a,MN=2a,则AB,CD,EF之间的关系为
,
AB,CD,MN之间的关系为
.
16.(2019?浙江湖州改编)已知∠α=60°32′,则90°﹣∠α为
.
17.
已知直线AB,点C是直线AB上一点,已知线段AB=10cm,线段BC=6cm.则线段AC的长为
.
18.(2019?通州区一模)如图9所示,在一条笔直公路的两侧,分别有A、B两个小区,为了方便居民出行,现要在公路上建一个公共自行车存放点,使存放点到A、B小区的距离之和最小,你认为存放点应该建在 处(填“C”“E”或“D”),理由是
.
19.已知∠AOC=64°,∠BOC=34°.则∠AOB的度数为
.
三、解答题(共8题,满分50分)
20.(满分9分)完成下表:
21.(满分4分)如图10,已知:同一平面内的三点A,B,C,按要求画图:
画线段AB;(2)画射线AC;(3)画直线BC.
22.
(满分4分)(2019年聊城)如图11,数轴上O,A两点的距离为4,一动点P从点A
出发,按以下规律跳动:第1次跳动到AO的中点处,第2次从点跳动到O的中点
处,第3次从点跳动到O的中点处,按照这样的规律继续跳动到点,,,…,
.(n≥3,n是整数)处,求线段A的长(n≥3,n是整数).
23.(满分7分)教材阅读与思考
下面是人教版七年级上册p127页上一段话,请仔细阅读,完成后面的问题:
如图4.2-11(1),点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点.类似地,还有线段的三等分点、四等分点等(图4.2-11(2)(3)),
(1)下列四种说法:①因为AM=MB,所以M是AB中点;②在线段AM的延长线上取一点B,如果AB=2AM,那么M是AB的中点;③因为M是AB的中点,所以AM=MB=AB;④因为A、M、B在同一条直线上,且AM=BM,所以M是AB中点,其中正确的是
(
)
A.①③④
B.④
C.
②③④
D.③④
(2)将一条线段分成相等线段的点叫线段的中点.这句话对吗?为什么?
(3)下列说法正确的是
( )
A、到线段两个端点距离相等的点叫做线段的中点
B、线段的中点到线段两个端点的距离相等
C、线段的中点可以有两个
D、线段的中点有若干个
(4)将一条绳子的两个绳头重合,折痕与绳子的交点,就是绳子的
.
24.
(满分6分如图12,把一个圆分成三个扇形,求出这三个扇形的圆心角.
25.
(满分6分在一条直线上任意取一点A,截取
AB=12cm,再截取AC=38cm,
点D是AB的中点,点E是AC的中点,求:D,E之间的距离.
26.
(满分6分
已知∠AOC=120°∠BOC=20°,OD是∠AOB的平分线,
OE是∠BOC
的平分线,求∠DOE的度数.
27.
(满分6分(2018?高邑县一模)如图13,已知A,B两点在数轴上,点A表示的数为﹣10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)(1)数轴上点B对应的数是 .
(2)经过几秒,点M、点N分别到原点O的距离相等?
参考答案:
一、选择题
1.C
2.
B
3.
C
4.
C
5.
A
6.
C
7.
B
8.B
9.B
10.
A
11.
C
12.C
二、填空题
13.两点确定一条直线.
14.
18.5
15.
EF=AB+CD;MN=CD-AB.
16.
29°28′
17.
16cm或4cm.
18.
E,两点之间线段最短.
19.
98°或30°.
三、解答题
20.解:
21.解:画图如下:
22.
解:由于OA=4,所有第一次跳动到OA的中点处时,O=OA,同理第二次从点跳动到处,离原点的距离为
O=OA,同理跳动n次后,离原点的距离:OA,所以A=OA-OA=4(1-)(n≥3,n是整数).
23.
解:(1)C
(2)
错误,没有指出是两条相等的线段;(3)B;(4)中点.
24.
解:三个扇形的圆心角分别为:360°×=108°;360°×=72°;360°×=180°.
25.
解:AB与AC重合的端点是点A,当点B,C在点A的同侧时,如图1所示,
因为点D是AB的中点,所以AD=BD=AB;因为点E是AC的中点,所以AE=AC,
因为DE=AE-AD,所以DE=AC-AB=
(AC-AB),
因为AB=12,AC=38,所以DE=
(38-12)=13(cm);
当点B,C在点A的异侧时,如图2所示,
因为点D是AB的中点,所以AD=BD=AB;因为点E是AC的中点,所以AE=AC,
因为DE=AE+AD,所以DE=AC+AB=
(AC+AB),
因为AB=12,AC=38,所以DE=38+12)=25(cm);所以线段DE的长为13cm或25cm.
26.
解:当∠BOC在∠AOC的外部时,如图1,因为OD是∠AOB的平分线,
OE是∠BOC
的平分线,所以∠BOD=∠AOB,∠EOB
=∠BOC,因为∠DOE=∠BOD-∠EOB,
所以∠DOE=∠AOB-∠BOC=
(∠AOB-∠BOC)=
(140°-20°)=60°;
当∠BOC在∠AOC的内部时,如图2,因为OD是∠AOB的平分线,
OE是∠BOC
的平分线,所以∠BOD=∠AOB,∠EOB
=∠BOC,因为∠DOE=∠BOD+∠EOB,
所以∠DOE=∠AOB+∠BOC=
(∠AOB+∠BOC)=
(100°+20°)=60°;
所以∠DOE的度数为60°.
27.
解:(1)因为点A表示的数为﹣10,所以OA=10;因为OB=3OA=30,所以B对应的数是30.
(2)设经过x秒,点M、点N分别到原点O的距离相等,此时点M对应的数为3x﹣10,点N对应的数为2x.
①点M、点N在点O两侧,则3x-10+2x=0,解得x=2;②点M、点N重合,则3x﹣10=2x,
解得x=10.所以经过2秒或10秒,点M、点N分别到原点O的距离相等.
参考答案:
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
