人教版数学八年级下册:18.2.2 菱形的性质 课件(共32张PPT)
文档属性
| 名称 | 人教版数学八年级下册:18.2.2 菱形的性质 课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-18 20:14:24 | ||
图片预览



文档简介
(共32张PPT)
人教版数学教材八年级下
特殊的平行四边形
-----菱形的性质
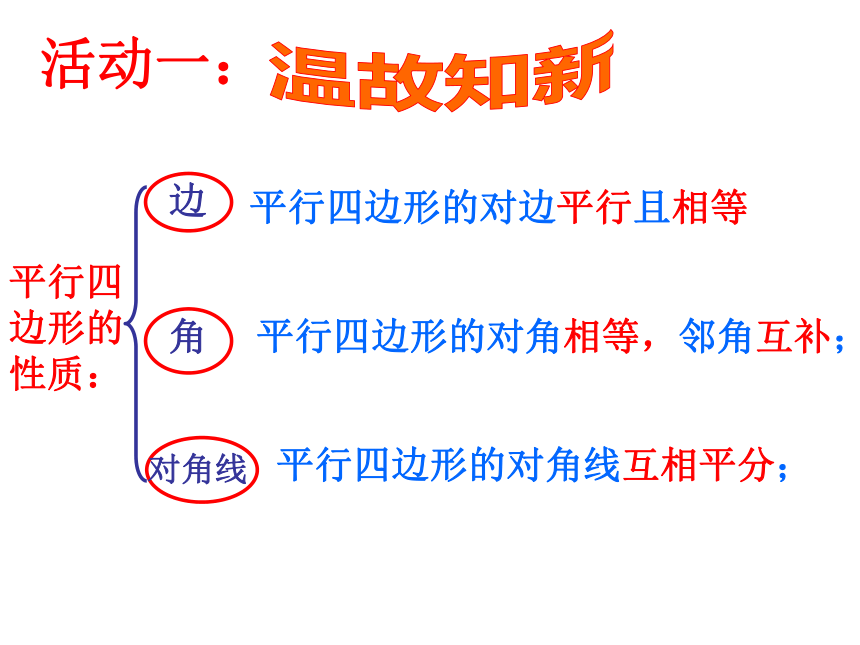
平行四边形的性质:
边
平行四边形的对边平行且相等
角
平行四边形的对角相等,邻角互补;
对角线
平行四边形的对角线互相平分;
活动一:
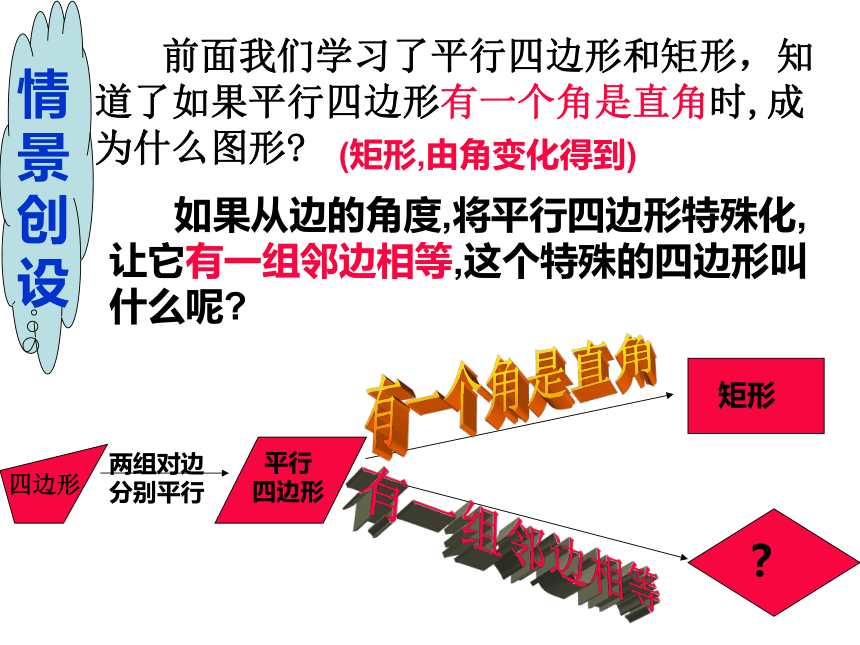
两组对边
分别平行
平行
四边形
矩形
前面我们学行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?
?
(矩形,由角变化得到)
如果从边的角度,将平行四边形特殊化,让它有一组邻边相等,这个特殊的四边形叫什么呢?
四边形
情景创设
常务副县长述职情况报告
述职报告
按照政府分工,我分管财税、发展改革、人事劳动、社会保障、
金融、统计、科技等项工作,并负责与县人大、政协的工作联系。xxxxx年,围绕“xxxxxx”战略,立足后发地区率先崛起,不断解放
思想,创新举措,扎实苦干,分管工作实现新跨越。
一、工作完成情况
具体表现是:分管全面完成计划、重点实现较大突破、整体实现
上档升级、更好服务全县大局。
----经济运行更快更好。主要经济指标均完成或超额完成年度计划,反映经济运行质量和速度的指标同比均有大幅增长。其,GDP预
计完成xxx亿元,同比增长xxx%,与计划持平;城镇固定资产投资
完成xx亿元,同比增长xxx%;财政收入完成xxx万元,同比增长xxx%,其,地方一般预算收入完成xxxx万元,同比增长xxx%;城
镇居民可支配收入达到xxx元,同比增长xxxx%;农民人均纯收入达
到xxx元,同比增长xxx%,全社会消费品零售总额预计达到xxx亿元,增长xxx%。
----财政收支科学高效。财政收支呈现出“增速加快、历史新高,
质量提升、结构优化,调度有方、保障有力”的特点。xxx年至xxxxx年,收入增幅分
有一个角
是直角
矩形
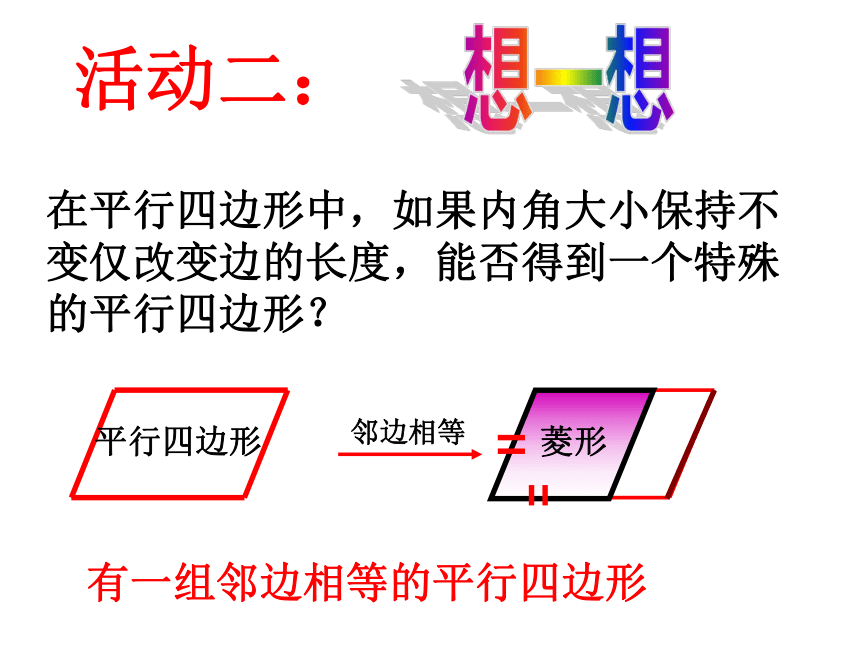
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
平行四边形
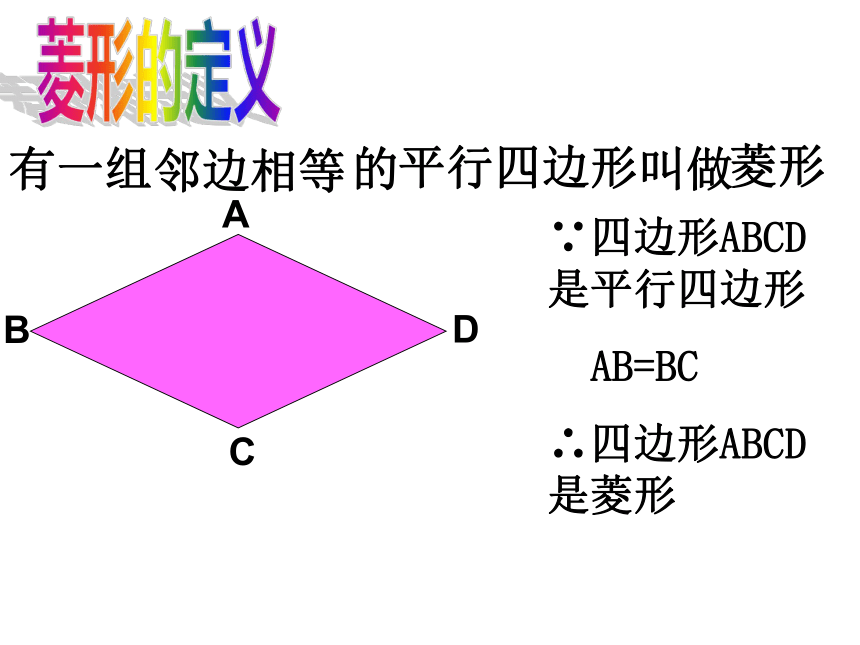
有一组邻边相等的平行四边形
菱形
邻边相等
活动二:
有一组
的
叫做
邻边相等
平行四边形
A
D
C
B
∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形
菱形
1、判断题
1、有一组邻边相等的四边形是菱形。
(
)
2、菱形是平行四边形。(
)
2、在我们的生活中,你见到过菱形
图案吗?请说出来。
3、平行四边形是菱形。(
)
菱形的性质的探究
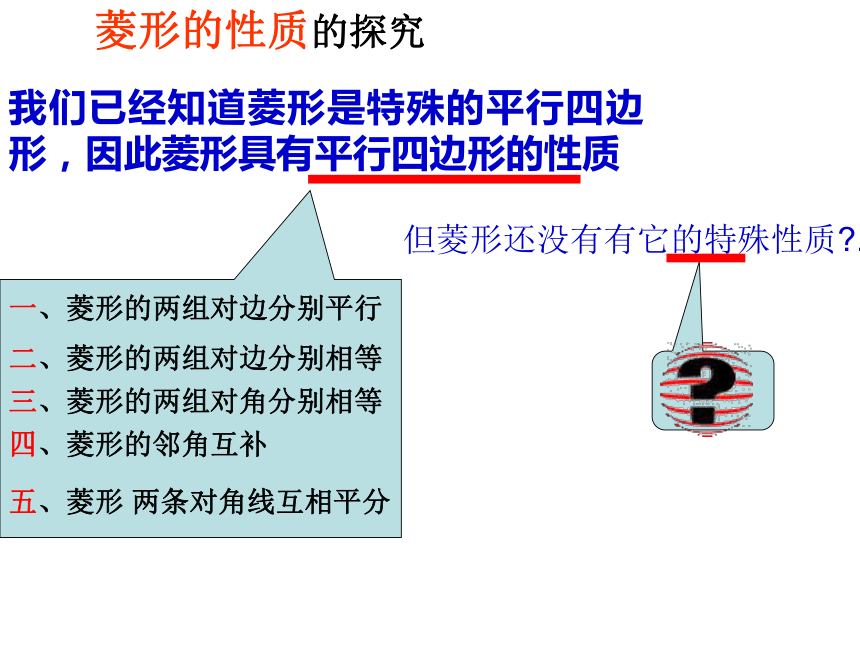
但菱形还没有有它的特殊性质?.
E
。
五、菱形
两条对角线互相平分
三、菱形的两组对角分别相等
二、菱形的两组对边分别相等
一、菱形的两组对边分别平行
四、菱形的邻角互补
我们已经知道菱形是特殊的平行四边形,因此菱形具有平行四边形的性质
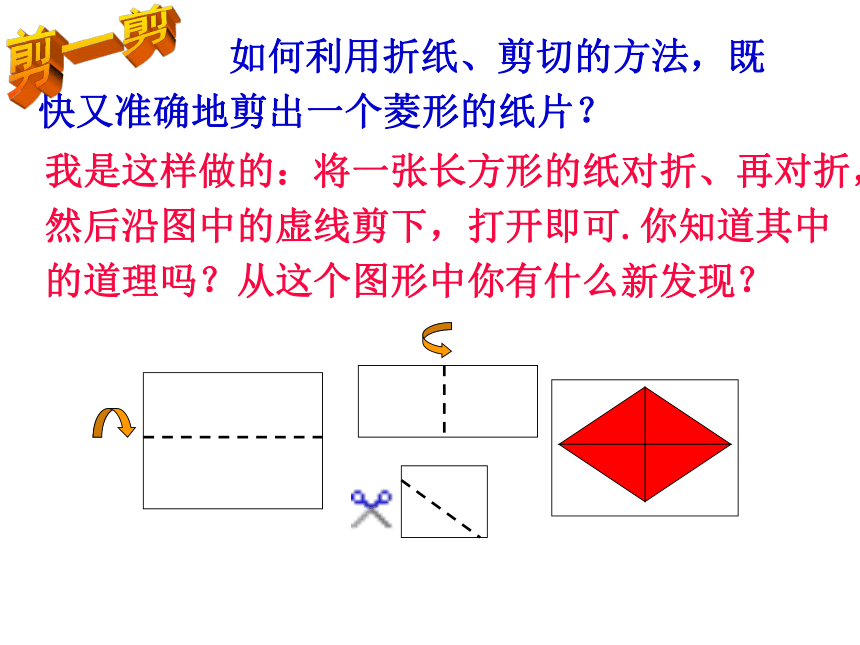
我是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?从这个图形中你有什么新发现?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
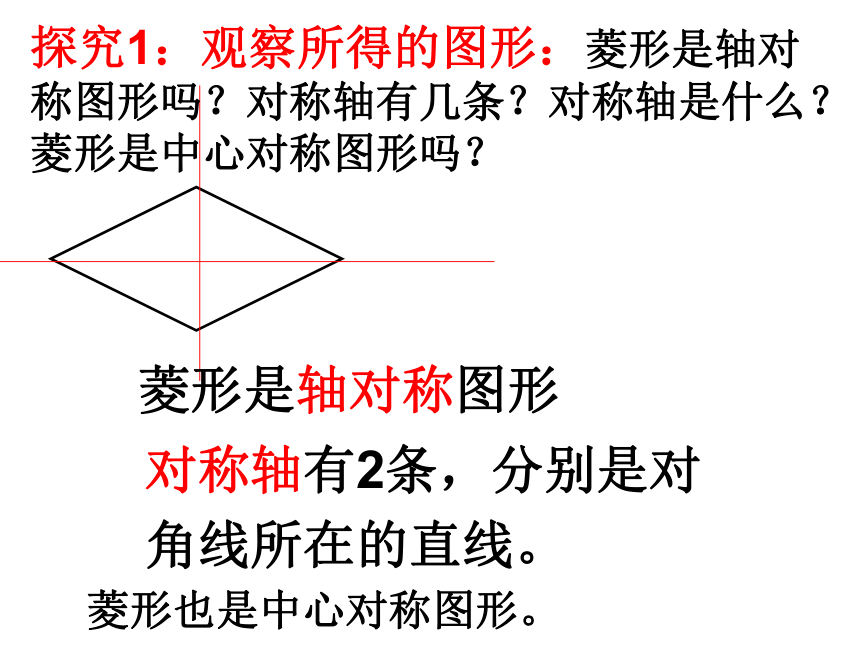
探究1:观察所得的图形:菱形是轴对称图形吗?对称轴有几条?对称轴是什么?菱形是中心对称图形吗?
菱形是轴对称图形
对称轴有2条,分别是对角线所在的直线。
菱形也是中心对称图形。
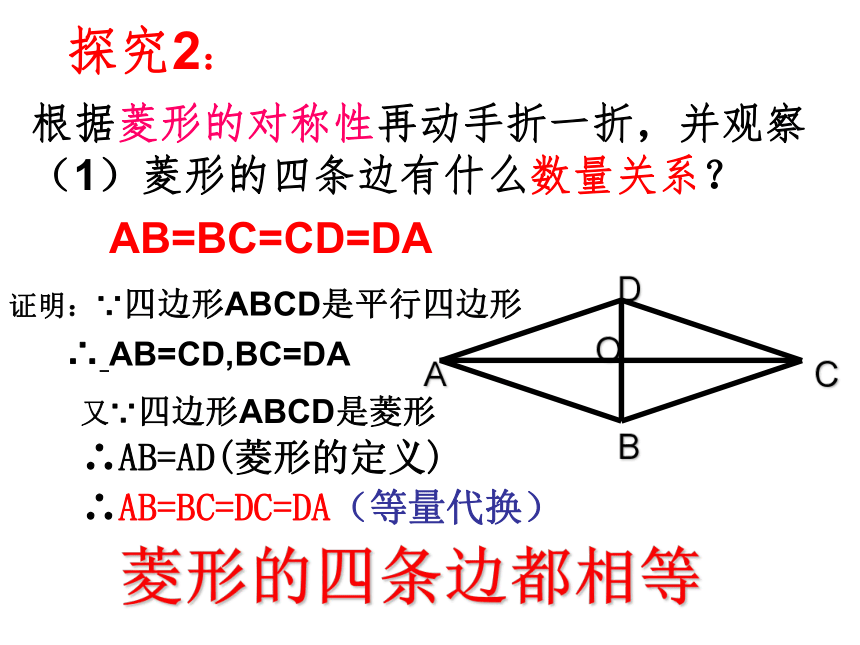
根据菱形的对称性再动手折一折,并观察(1)菱形的四条边有什么数量关系?
探究2:
AB=BC=CD=DA
证明:∵四边形ABCD是平行四边形
∴
AB=CD,BC=DA
又∵四边形ABCD是菱形
∴AB=AD(菱形的定义)
∴AB=BC=DC=DA(等量代换)
A
B
C
D
O
菱形的四条边都相等
根据菱形的对称性再动手折一折,并观察菱形的对角线AC和BD有什么位置关系?
探究3:
3
4
5
6
7
1
8
2
D
C
B
A
O
观察∠1与∠2,∠5与∠6
,
∠3与∠4,∠7与∠8
在数量上有什么关系?
菱形的对角线互相垂直,
并且每一条对角线平分一组对角.
小组合作完成性质的证明.
A
B
D
C
O
(1)菱形是轴对称图形,对称轴有两条,是菱形两条对角线所在的直线.菱形也是中心对称图形。
(2)菱形的四条边都相等
(3)菱形的两条对角线互相垂直,每一条对角线平分一组对角。
思考:特殊在?
菱形的四边相等
菱形的对角线互相垂直,
并且每一条对角线平分一组对角
菱形特有的性质
边:
对角线:
对称性:
菱形是轴对称图形,也是中心对称图形
A
D
C
B
O
边
角
对角线
对称性
菱形的两组对边平行且相等
几何语言
∵四边形ABCD是菱形
∥
=
∴
AD
BC
AB
CD
∥
=
菱形的四条边相等
∴
AB=BC=CD=DA
菱形的两组对角分别相等
∴
∠DAB=∠DCB
∠ADC=∠ABC
菱形的邻角互补
∴
∠DAB+∠ABC=
180°
菱形的两条对角线互相平分
∴
OA=OC;OB=OD
菱形的两条对角线互相垂直,
每一条对角线平分一组对角。
∴
AC⊥BD
∠1=∠2
∠3=∠4
∠5=∠6
∠7=∠8
菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。菱形也是中心对称图形
1
2
4
3
5
7
6
8
A
D
C
B
O
∵四边形ABCD是菱形,
1、说说理由
∴AD∥BC,AB∥CD
(
)
AB=BC=CD=DA
(
)
OA=OC,OB=OD
(
)
AC⊥BD
(
)
∠ADB=∠CDB=∠ABD=∠CBD
=
∠ADC=
∠ABC
(
)
2、(多选题)下面性质中菱形有而矩形没有的是(
)
A、邻角互补
B、内角和为360°
C、对角线相等
D、对角线互相垂直
E、四条边相等
F、每一条对角线平分一组对角
G、中心对称图形
H、轴对称图形
D、E、F
应用新知
3、已知菱形的周长是12cm,那么它的边长是______.
4、菱形ABCD中,对角线AC=10,BD=24,则AB=_______.
3cm
13
6、如图,在菱形ABCD中,已知
∠ABD=20°,
则
∠ABC=___,∠C=______.
5、如图,在菱形ABCD中,AB=5,
∠BCD=120°,则对角线AC=_______.
A
B
C
D
A
B
C
D
5
40°
140°
应用新知
7、菱形ABCD中∠DAO=30°,那么∠ABD的度数是(
)。
C
B
D
A
O
30
°
600
应用新知
8、已知菱形的两条对角线分别是6cm和8cm,那么它的周长是
。
20cm
C
B
D
A
O
3
4
注意:有关菱形问题可转化为直角三角形的问题来解决
5
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
9、已知四边形ABCD是菱形
AB=CD=AD=BC
OA=OC
OB=OD
∠DAB=∠BCD
∠ABC
=∠CDA
∠AOB=∠DOC=∠AOD=∠BOC
=90°
∠1=∠2=∠3=∠4
∠5=∠6=∠7=∠8
△ABC
△
DBC
△ACD
△ABD
Rt△AOB
Rt△BOC
Rt△COD
Rt△DOA
Rt△AOB
≌
Rt△BOC≌
Rt△COD
≌
Rt△DOA
△ABD≌△BCD
△ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
【菱形的面积公式】
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积吗?
菱形
A
B
C
D
O
E
S菱形=BC·
AE
思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗?
再探新知
C
B
D
A
O
菱形面积
如图:四边形ABCD是菱形,
O是对角线交点,
用AC和OD表示△ACD的面积,
用AC和OB表示出△ABC的面积。
(2)求出菱形ABCD的面积,你有什么发现?
S菱形=
两对角线积的一半
C
B
D
A
O
E
S菱形=底×高=
两对角线积的一半
记住菱形面积2个公式:
1.已知菱形边长是10,高是6,那么它的面积是
。
2.如图:菱形的对角线分别是10和8,则菱形的面积是(
)
60
40
C
B
D
A
O
8
10
3、在任意四边形ABCD中,对角线AC⊥BD
,且AC=18,BD=10。问四边形ABCD的面积是多少?
ABCD=S△ABD+S△BCD
S
=
BD·AO
+
BD·CO
=
·BD·
(AO+CO)
=
BD·AC
=
×10×18=90
解:
D
A
O
B
C
你有什么
发现?
4、
如图,菱形花坛ABCD的边长为10m,BO=8m,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积。
A
B
C
D
O
1、在菱形ABCD中,AE⊥BCAF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是(
)
A.75°
B.60°
C.45°
D.30°
B
能力提升
2、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。
A
B
C
D
E
O
A
B
C
D
E
O
2
∵四边形ABCD是菱形,
∴AD=AB
解:
∴AD=AB=BD
∵
E是AB的中点,且DE⊥AB
∴DA=DB(
)
∴
∠DAB=
60
°,
∴
∠ABC=120
°
(2)
∵AE=2,
∴
AB=4
∴
BD=AB=4
∵四边形ABCD是菱形,∴
AC⊥DB
∵
DB=4
∴
0B=2
∴
在R
t△AOB中,由勾股定理得
2
AO=
∴
AC=4
(3)
在Rt△DAE中,由勾股定理得
DE=
=2
∴
S菱形ABCD=4×2
=8
(1)
谈一谈这一节课的收获!
A
D
C
B
O
边
角
对角线
对称性
菱形的两组对边平行且相等
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相平分
菱形的两条对角线互相垂直,
每一条对角线平分一组对角。
菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。菱形也是中心对称图形
1
2
4
3
5
7
6
8
1个定义
2个公式
3个特殊
:有一组邻边相等的平行四边形叫菱形
:S菱形=底×高
S菱形=
两条对角线乘积的一半
:特在“边、对角线、对称性”
人教版数学教材八年级下
特殊的平行四边形
-----菱形的性质
平行四边形的性质:
边
平行四边形的对边平行且相等
角
平行四边形的对角相等,邻角互补;
对角线
平行四边形的对角线互相平分;
活动一:
两组对边
分别平行
平行
四边形
矩形
前面我们学行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?
?
(矩形,由角变化得到)
如果从边的角度,将平行四边形特殊化,让它有一组邻边相等,这个特殊的四边形叫什么呢?
四边形
情景创设
常务副县长述职情况报告
述职报告
按照政府分工,我分管财税、发展改革、人事劳动、社会保障、
金融、统计、科技等项工作,并负责与县人大、政协的工作联系。xxxxx年,围绕“xxxxxx”战略,立足后发地区率先崛起,不断解放
思想,创新举措,扎实苦干,分管工作实现新跨越。
一、工作完成情况
具体表现是:分管全面完成计划、重点实现较大突破、整体实现
上档升级、更好服务全县大局。
----经济运行更快更好。主要经济指标均完成或超额完成年度计划,反映经济运行质量和速度的指标同比均有大幅增长。其,GDP预
计完成xxx亿元,同比增长xxx%,与计划持平;城镇固定资产投资
完成xx亿元,同比增长xxx%;财政收入完成xxx万元,同比增长xxx%,其,地方一般预算收入完成xxxx万元,同比增长xxx%;城
镇居民可支配收入达到xxx元,同比增长xxxx%;农民人均纯收入达
到xxx元,同比增长xxx%,全社会消费品零售总额预计达到xxx亿元,增长xxx%。
----财政收支科学高效。财政收支呈现出“增速加快、历史新高,
质量提升、结构优化,调度有方、保障有力”的特点。xxx年至xxxxx年,收入增幅分
有一个角
是直角
矩形
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
平行四边形
有一组邻边相等的平行四边形
菱形
邻边相等
活动二:
有一组
的
叫做
邻边相等
平行四边形
A
D
C
B
∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形
菱形
1、判断题
1、有一组邻边相等的四边形是菱形。
(
)
2、菱形是平行四边形。(
)
2、在我们的生活中,你见到过菱形
图案吗?请说出来。
3、平行四边形是菱形。(
)
菱形的性质的探究
但菱形还没有有它的特殊性质?.
E
。
五、菱形
两条对角线互相平分
三、菱形的两组对角分别相等
二、菱形的两组对边分别相等
一、菱形的两组对边分别平行
四、菱形的邻角互补
我们已经知道菱形是特殊的平行四边形,因此菱形具有平行四边形的性质
我是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?从这个图形中你有什么新发现?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
探究1:观察所得的图形:菱形是轴对称图形吗?对称轴有几条?对称轴是什么?菱形是中心对称图形吗?
菱形是轴对称图形
对称轴有2条,分别是对角线所在的直线。
菱形也是中心对称图形。
根据菱形的对称性再动手折一折,并观察(1)菱形的四条边有什么数量关系?
探究2:
AB=BC=CD=DA
证明:∵四边形ABCD是平行四边形
∴
AB=CD,BC=DA
又∵四边形ABCD是菱形
∴AB=AD(菱形的定义)
∴AB=BC=DC=DA(等量代换)
A
B
C
D
O
菱形的四条边都相等
根据菱形的对称性再动手折一折,并观察菱形的对角线AC和BD有什么位置关系?
探究3:
3
4
5
6
7
1
8
2
D
C
B
A
O
观察∠1与∠2,∠5与∠6
,
∠3与∠4,∠7与∠8
在数量上有什么关系?
菱形的对角线互相垂直,
并且每一条对角线平分一组对角.
小组合作完成性质的证明.
A
B
D
C
O
(1)菱形是轴对称图形,对称轴有两条,是菱形两条对角线所在的直线.菱形也是中心对称图形。
(2)菱形的四条边都相等
(3)菱形的两条对角线互相垂直,每一条对角线平分一组对角。
思考:特殊在?
菱形的四边相等
菱形的对角线互相垂直,
并且每一条对角线平分一组对角
菱形特有的性质
边:
对角线:
对称性:
菱形是轴对称图形,也是中心对称图形
A
D
C
B
O
边
角
对角线
对称性
菱形的两组对边平行且相等
几何语言
∵四边形ABCD是菱形
∥
=
∴
AD
BC
AB
CD
∥
=
菱形的四条边相等
∴
AB=BC=CD=DA
菱形的两组对角分别相等
∴
∠DAB=∠DCB
∠ADC=∠ABC
菱形的邻角互补
∴
∠DAB+∠ABC=
180°
菱形的两条对角线互相平分
∴
OA=OC;OB=OD
菱形的两条对角线互相垂直,
每一条对角线平分一组对角。
∴
AC⊥BD
∠1=∠2
∠3=∠4
∠5=∠6
∠7=∠8
菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。菱形也是中心对称图形
1
2
4
3
5
7
6
8
A
D
C
B
O
∵四边形ABCD是菱形,
1、说说理由
∴AD∥BC,AB∥CD
(
)
AB=BC=CD=DA
(
)
OA=OC,OB=OD
(
)
AC⊥BD
(
)
∠ADB=∠CDB=∠ABD=∠CBD
=
∠ADC=
∠ABC
(
)
2、(多选题)下面性质中菱形有而矩形没有的是(
)
A、邻角互补
B、内角和为360°
C、对角线相等
D、对角线互相垂直
E、四条边相等
F、每一条对角线平分一组对角
G、中心对称图形
H、轴对称图形
D、E、F
应用新知
3、已知菱形的周长是12cm,那么它的边长是______.
4、菱形ABCD中,对角线AC=10,BD=24,则AB=_______.
3cm
13
6、如图,在菱形ABCD中,已知
∠ABD=20°,
则
∠ABC=___,∠C=______.
5、如图,在菱形ABCD中,AB=5,
∠BCD=120°,则对角线AC=_______.
A
B
C
D
A
B
C
D
5
40°
140°
应用新知
7、菱形ABCD中∠DAO=30°,那么∠ABD的度数是(
)。
C
B
D
A
O
30
°
600
应用新知
8、已知菱形的两条对角线分别是6cm和8cm,那么它的周长是
。
20cm
C
B
D
A
O
3
4
注意:有关菱形问题可转化为直角三角形的问题来解决
5
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
9、已知四边形ABCD是菱形
AB=CD=AD=BC
OA=OC
OB=OD
∠DAB=∠BCD
∠ABC
=∠CDA
∠AOB=∠DOC=∠AOD=∠BOC
=90°
∠1=∠2=∠3=∠4
∠5=∠6=∠7=∠8
△ABC
△
DBC
△ACD
△ABD
Rt△AOB
Rt△BOC
Rt△COD
Rt△DOA
Rt△AOB
≌
Rt△BOC≌
Rt△COD
≌
Rt△DOA
△ABD≌△BCD
△ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
【菱形的面积公式】
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积吗?
菱形
A
B
C
D
O
E
S菱形=BC·
AE
思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积公式吗?
再探新知
C
B
D
A
O
菱形面积
如图:四边形ABCD是菱形,
O是对角线交点,
用AC和OD表示△ACD的面积,
用AC和OB表示出△ABC的面积。
(2)求出菱形ABCD的面积,你有什么发现?
S菱形=
两对角线积的一半
C
B
D
A
O
E
S菱形=底×高=
两对角线积的一半
记住菱形面积2个公式:
1.已知菱形边长是10,高是6,那么它的面积是
。
2.如图:菱形的对角线分别是10和8,则菱形的面积是(
)
60
40
C
B
D
A
O
8
10
3、在任意四边形ABCD中,对角线AC⊥BD
,且AC=18,BD=10。问四边形ABCD的面积是多少?
ABCD=S△ABD+S△BCD
S
=
BD·AO
+
BD·CO
=
·BD·
(AO+CO)
=
BD·AC
=
×10×18=90
解:
D
A
O
B
C
你有什么
发现?
4、
如图,菱形花坛ABCD的边长为10m,BO=8m,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积。
A
B
C
D
O
1、在菱形ABCD中,AE⊥BCAF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是(
)
A.75°
B.60°
C.45°
D.30°
B
能力提升
2、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。
A
B
C
D
E
O
A
B
C
D
E
O
2
∵四边形ABCD是菱形,
∴AD=AB
解:
∴AD=AB=BD
∵
E是AB的中点,且DE⊥AB
∴DA=DB(
)
∴
∠DAB=
60
°,
∴
∠ABC=120
°
(2)
∵AE=2,
∴
AB=4
∴
BD=AB=4
∵四边形ABCD是菱形,∴
AC⊥DB
∵
DB=4
∴
0B=2
∴
在R
t△AOB中,由勾股定理得
2
AO=
∴
AC=4
(3)
在Rt△DAE中,由勾股定理得
DE=
=2
∴
S菱形ABCD=4×2
=8
(1)
谈一谈这一节课的收获!
A
D
C
B
O
边
角
对角线
对称性
菱形的两组对边平行且相等
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相平分
菱形的两条对角线互相垂直,
每一条对角线平分一组对角。
菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。菱形也是中心对称图形
1
2
4
3
5
7
6
8
1个定义
2个公式
3个特殊
:有一组邻边相等的平行四边形叫菱形
:S菱形=底×高
S菱形=
两条对角线乘积的一半
:特在“边、对角线、对称性”
