2020-2021年新高三数学一轮复习考点 函数的图象(含解析)
文档属性
| 名称 | 2020-2021年新高三数学一轮复习考点 函数的图象(含解析) |  | |
| 格式 | |||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-19 18:44:41 | ||
图片预览




文档简介
2020-2021 年新高三数学一轮复习考点 函数的图象
1.最新考试说明:
① 在实际情境中,会根据不同的需要选择图象法、列表法、解析法表示函数.
【 2020年高考北京卷 15】 为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达
标的企业要限期整改.设企业的污水排放量 与时间 的关系为 ,用 的大小评
价在 这段时间内企业污水治理能力的强弱. 已知整改期内,甲、乙两企业的污水排放量与时间的关
系如下图所示.
给出下列四个结论 :
① 在 这段时间内 , 甲企业的污水治理能力比乙企 业强 ;
②在 时刻,甲企业的污水治理能力比乙企业强;
③ 在 时刻 , 甲 、 乙两企业的污水排放量都已达标 ;
④ 甲企业在 , , 这三段时间中 , 在 的污水治理能力最强.
其中所有正确结论的 序号是 .
【答案】 ①②③
【解析】∵ 用 来评价治污能力 ,而 是图像上两点连线的斜率 ,在
上 , 甲的治污能力比乙强 , 故 ①对, 时刻甲比乙强 , 时刻都低于达标排放量 ,∴都达标,甲企业在
时刻治污能力不是最强 .
【专家解读】本题的特点是注重 知识的灵活运用 ,本题考查了 函数图象及其性质的综合应用 ,考 查 数形结
合思想 ,考查数学运算 、数学直观、逻辑推理等 学科素养.解题关键是正确 接函数的图像及其性质解决问
题.
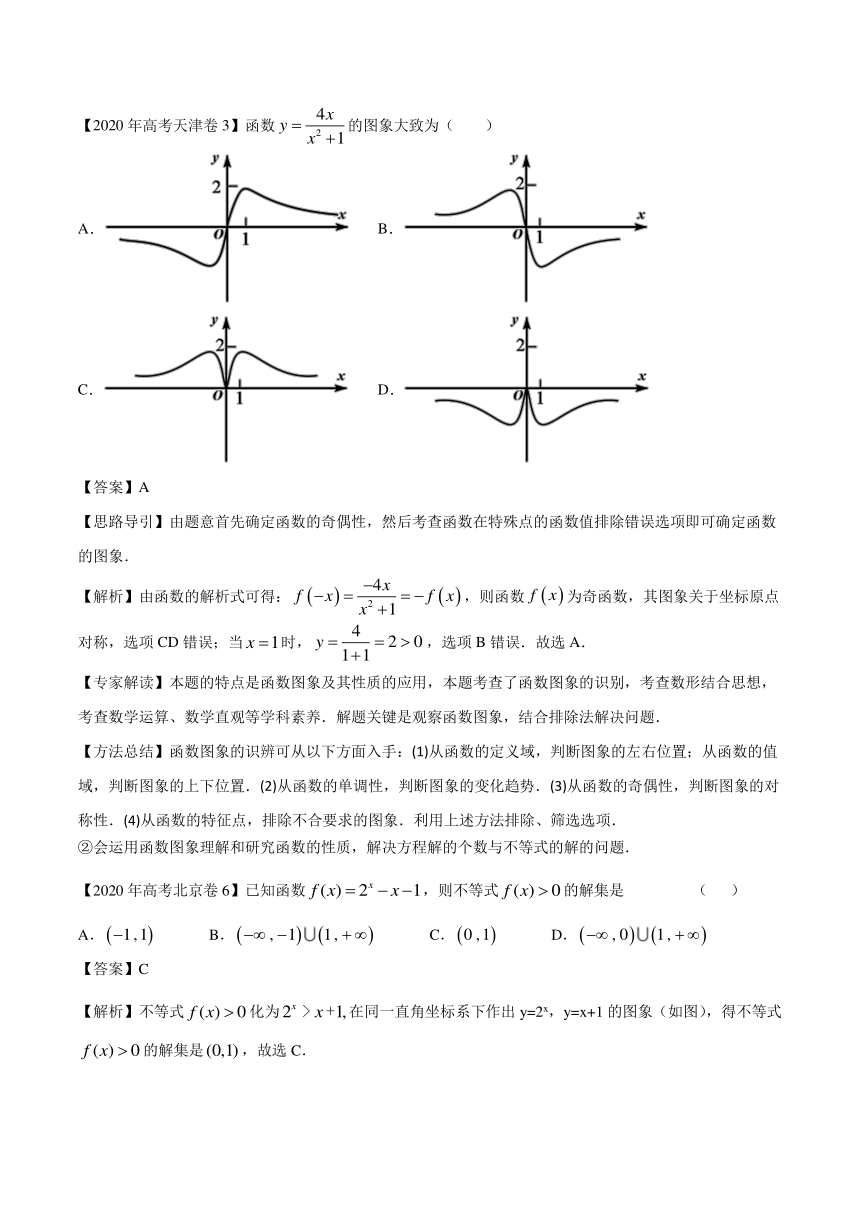
【 2020年高考天津卷 3】 函数 的图象大致为( )
A. B.
C. D.
【答案】 A
【思路导引】 由题意首先确定函数的奇偶性,然后考查函数在特殊点的函数值排除错误选项即可确定函数
的图象 .
【解析】 由函数的解析式可得: ,则函数 为奇函数,其图象关于坐标原点
对称,选项 CD错误;当 时, ,选项 B错误 . 故选 A.
【专家解读】本题的特点是 函数图象及其性质的应用 ,本题考查了 函数图象的识别 ,考查 数 形结合思想 ,
考查数学运算 、数学直观等 学科素养.解题关键是 观察函数图象,结合排除法解决问题.
【方法总结】 函数图象的识辨可从以下方面入手: (1)从函数的定义域,判断图象的左右位置;从函数的值
域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势. (3)从函数的奇偶性,判断图象的对
称性. (4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.
② 会运用函数图象理解和研究函数的性质,解决方程解的个数与不等式的解的问题.
【 2020年高考北京卷 6】 已知函数 ,则不等式 的解集是 ( )
A. B. C. D.
【答案】 C
【解析】 不等式 化为 在同一直角坐标系下作出 y=2x, y=x+1的图象(如图),得 不等式
的解集是 , 故选 C.
【专家解读】本题考查了 简单指数 不等式的解法,考查 数形结合思想 ,考查数学运算 、数学直观 学科素养.解
题关键是正确 作出函数图象,利用图象解决问题.
【 2020年高考浙江卷 9】 已知 且 ,若 在 上恒成立,则
( )
A. B. C. D.
【答案】 C
【思路导引】 对 分 与 两种情况讨论,结合三次函数的性质分 析即可得到答案 .
【解析】 当 时,在 上, 恒成立,∴只需满足 恒成立,此时
,由二次函数的图象可知,只有 时,满足 , 不满条件;
当 时,在 上, 恒成立,∴只需满足 恒成立,此时当两根分别
为 和 ,
( 1)当 时,此时 ,当 时, 不恒成立,
( 2)当 时,此时 ,若满足 恒成立,只需满足
当 时,此时 ,满足 恒成立,
综上可知满足 在 恒成立时,只有 ,故选 C .
【专家解读】本题的特点是 知识的灵活运用 ,本题考查了三次函数在给定区间上恒成立问题,考查 数形结
合及 分类讨论思想,考查 数学运算 、数学直观、逻辑推理等 学科素养.解题关键是 合理分类,做到不重不
漏.
③ 会用数形结合思想、转化与化归思想解决数学问题 .
【 2020 年高考上海卷 11】 已知 , 若存在定义域为 的函数 同时满足下列两个条件 ,①对任意
, 的值为 或 ;②关于 的方程 无实数解 ; 则 的取值范围为 .
【答案】
【解析】由 和 的图象和函数的定义可知,若满足 的值为 或 ,只有
, ,结合②可知若方程 无实数解,则 ,
故答案为: .
【专家解读】本题的特点是 函数图象及其性质的应用 ,本题考查了 函数与方程 ,二次函数图象及其应用 ,
考查 函数与方程思想、数形结合思想 ,考查数学运算 、数学直观、数学建模等 学科素养.解题关键是正确
作出函数图象,应用函数图象及其性质解决问题.
【 2020年高考天津卷 9】 已知函数 若函数 恰有 4个
零点,则 的取值范围是( )
A. B.
C. D.
【答案】 D
【思路导引】 由 ,结合已知,将问题转化为 与 有 个不同交点,分
三种情况,数形结合讨论即可得到答案 .
【解析】 注意到 ,所以要使 恰有 4个零点,只需方程 恰有 3个实根 , 即可,
令 ,即 与 的图象有 个不同交点 . 因为 ,
当 时,此时 ,如图 1, 与 有 个不同交点,不满足题意;当 时,如图
2,此时 与 恒有 个不同交点,满足题意;当 时,如图 3,当 与
相切时,联立方程得 ,令 得 ,解得 (负值舍去),所以 .
综上, 的取值范围为 , 故选 D.
【专家解读】本题的特点是 函数图象及其现在的灵活运用 ,本题考查了 函数与方程的应用,考查数形结合 、
分类讨论、 转化与化归 等数学 思想 方法 ,考查数学运算 、直观想象、数学建模等 学科素养.解题关键是正
确 作出函数图象,应用函数图象及其性质解 决问题.
2.命题方向预测:
从近 二 年的高考试题来看,主要考查图象的辨识以及利用图象研究函数的性质、方程 及 不等式的解,多以
选择题 、填空题 的形式出现,属中低档题,主要考查基本初等函数的图象及应用 .
预测 2017年高考对本节内容的考查仍将以 函数图象识别与 函数图象的应用为主, 依然体现“有图考图”“无
图考图”的原则, 题型 仍为 选择题 或填空题 的形式.备考时要求熟练掌握各种基本初等函数的图象及性质,
加强函数性质的应用意识,另外还应熟练掌握各种图象变换的法则 .
3.课本结论总结:
( 1) 画函数图象的一般方法
①描点法 :当函 数表达式 (或变形后的表达式 )是熟悉的基本函数时,就可根据这些函数的特征直接作出 ,
其步骤为: 先确定函数的定义域,化简给定的函数解析式,再根据化简后的函数解析式研究函数的值域、
单调性、奇偶性、对称性、极值、最值,再根据函数的特点取值、列表,描点,连线,注意取点,一定要
包括关键点,如极值点、与 轴的交点等.
② 图象变换法:若函数图象可由某个基本函数的图象经过平移、翻折、对称得到,可利用图象变换作出,
但要注意变换顺序,对不能直接找到熟悉的基本函数的要先变形,并应注意 平移变换与伸缩变换的顺序对
变换单位及解析式的影响.
( 2)常见的图象变换
①平移变换:
左右平移: 函数 的图象可由函数 的图象向左( +)或向右( — )平移 个单位
得到;
上下平移: ( )的图象可由函数 的图象向上( +) 或向下( — )平移 个单位
得到;
②伸缩变换
函数 是将函数 图象上各点的纵坐标不变,横坐标变为原来的 得到;
函数 是将函数 图象上各点的横坐标不变,纵坐标变为原来的 A倍的得到;
③对称变换
函数 图象关于 轴对称得到函数 图象;
函数 图象关于 轴对称得到函数 图象;
函数 图象关于原点对称得到函数 图象;
函数 图象关于直线 对称得到函数为 图象.
④翻折变换
函数 的图象这样得到:函数 在 轴右侧的图象保持不变,左侧的图象去掉后,再将右
侧的图象翻折到 轴左侧(函数 为偶函数,其图象关于 轴对称) ;
函数 的图象是这样得到的:函数 在 轴上方的图象保持不变,把下方的图象关于 轴
对称到上方(注意到函数 的函数值都大于零).
4.名师二级结 论:
( 1)函数图象的几个应用
①判断函数的奇偶性、确定单调区间:图象关于原点对称是奇函数,图象关于 y轴对称是偶函数 .图象从左
到右上升段对应的 的取值范围是增区间,下降对应的 的取值范围 是减区间 .
②方程 的根就是函数 与函数 图象交点的横坐标 .
③不等式 的解集是函数 的图象在函数 图象上方的一段对应的 的取值范围
(交点坐标要通过解方程求得)
( 2)函数 的图象的 对称性
①若函数 关于 对称 对定义域内任意 都有 = 对定义域内任意 都
有 = 是偶函数;
②函数 关于点( , 0)对称 对定义域内任意 都有 =- =-
是奇函数;
③若 函数 对定义域内任意 都有 ,则 函数 的对称轴是 ;
④若 函数 对定义域内任意 都有 ,则 函数 的对称轴中心为 ;
⑤ 函数 关于 对称 .
(3) 明确函数图象形状和位置的方法大致有以下三种途径.
① 图象变换:平移变换、伸缩变换、对称变换.
② 函数解析式的等价变换.
③ 研究函数的性质.
5.课本经典习题:
(1)新课标 A版第 23 页,练习第 2 题
下图中哪几个图象与下述三个事件分别吻合的最好?请你为剩下的那个图象写出一个事件 .
(1) 我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到作业本在上学;
(2) 我骑车一路匀速行驶,只是在途中遇到一次交通堵塞,耽误了一些时间;
(3) 我出发后,心情轻松,缓缓前进,后来为了赶时间开始加速 .
【经典理由】本题主要考查了图象识别,与高考题中的图象识别题很类似
(2) 新课标 A版第 25 页,习题 1.2 B组第 1 题
函数 的图象如图所示(图中曲线 与直线 无限接近,但永不相交) .
①函数 的定义域是什么?
②函数 的值域是什么?
③ 取何值时,只有唯一的 与之对应?
【经典理由】本题主要考查了图象应用,与高考题中的图象识应用很类似
6.考点交汇展示:
(1)与参数范围问 题交汇
【例】 ( 2020·甘肃省静宁县第一中学高三) 已知函数 ,若函数
有 4个零点,则实数 的取值范围是 ( )
A. B.
C. D.
【答案】 B
【解析】 函数 ,函数 有 4个零点,即 有四个不同
交点 .画出函数 图像如下图所示:
由图可知,当 时,设对应二次函数顶点为 ,则 , ,当 时,设
对应二次函数的顶点为 ,则 , .所以 .当直线 与 时的
函数图像相切时与函数 图像有三个交点,此时 ,化简可得 .
,解得 (舍);当直线 与 时的函数图
像相切时与函数 图像有五个交点,此时 , 化简可得 .
,解得 (舍);故当 有四个不同交点时
.
【例 2】 函数 的图象如图所示,则下列结论成立的是( )
( A) , , ( B) , ,
( C) , , ( D) , ,
【答案】 C
【解析】 由 及图象可知, , ,则 ;当 时, ,所以
;当 , ,所以 ,所以 .故 , , ,选 C.
(2)与函数性质交汇
【例】 ( 2020·陕西省西安中学高 三 ) 已知定义在 R上的函数 对任意的 x都满足 ,
当 时, .若函数 恰有 6个不同零点,则 a的取值范围是( )
A. B. C. D.
【答案】 A
【解析】 由条件可知函数 恰有 6个不同的零点,转化为 与 恰
有 6个不同的交点, , 的周期 ,且 时, ,
是偶函数,图象关于 轴对称,如图,在同一坐标系下画出函数 和 的图
象, ① 当 时, 的图象如图所示, 轴左侧有 4个交点,右侧有 2个交点,
此时应满足 ,解得 ;
② 当 时, 与 在 轴左侧有 2个交点,右侧有 4个交点,
此时应满足 ,解得: ;综上可知, 的取值范围是 .
【例 4】 在同一直坐标系中,一次函数 与二次函数 的图像可能是( )
A. B.
C. D.
【答案】 B
【解析】 因为直线 恒过点( 0, 1),所以舍去 A; 二次函数 开口向上,所以舍去 C;当
时,二次函数 顶点在 x轴上方,所以舍去 D,选 B.
(3)与函数零点问题交汇
【例 5】已知 是定义在 上的奇函数 , 且 ,则函数 的
零点个数为 ( )
A. B. C. D.
【答案】 D
【解析】 由 ,得 ,函数 的
零点,即方程 的根,也就是函数 与 交点的横坐标,结合函数
为实数集上的奇函数,作出图象如图,由图可知,函数 的零点个数 个.
故选 D.
( 4)与不等式交汇
【例 6】 ( 2019·定远县育才学校高 三) 已知函数 ,若不等式 恒成
立,则实数 的取值范围是( )
A. B. C. D.
【答案】 D
【解析】 画出函数 f( x) 的图象 ,
由 y= 可得直线在 y轴上的截距为 4, 若 4 恒成立 , 图像恒在分段函数的上
方,故
【例 7】 若 ,则 的取值范围是( )
A. B. C. D.
【答案】 C
【解析】
设 ,联立 得 ,因为 ,所以 ,
由它们的图象可知 的取值范围是 .
( 5)与方程交汇
【例 8】( 2020·浙江省高 三 ) 已知函数 ,若关于 的方程
有且仅有三个不同的整数解,则实数 的取值范围是( )
A. B. C. D.
【答案】 A
【解析】 , 函数 位于直线
和 的图象上有三个横坐标为整数的点 .当 时, 且 ,
由双勾函数的单调性可知,函数 在区间 上单调递减,在区间 上单调递增,
当 时, , , , , ,
且 ,如下图所示:要使得函数 位于直线 和 的图象上有
三个横坐标为整数的点,则 ,即 ,解得 .
因此,实数 的取值范围是 .
【 考点分类 】
热点 1 函数图象的识别
1.( 2020·四川省仁寿一中高三) 函数 图象的大致形状是( )
A. B. C. D.
【答案】 B
【解析】 ,
,故 为奇函数,排除选项 A、 C;又 ,排除 D,选 B.
2.( 2020·河北省衡水中学高三三模) 如图,是函数 的部分图象,则 的解析式可能是( )
A. B.
C. D.
【答案】 B
【解析】 由图像可知,函数图像关于 轴对称,所以 应为偶函数,所以排除 A;由图像可知函数值能
取到小于 0的值,所以排除 C;对于当 时, ,而当
时, ,而正弦的函数图像可知 D不正确 ,
3.若函数 ( 且 )过定点 ,且 在定义域 上是减函数,则
的图象是( )
A. B. C. D.
【答案】 A
【解析 】 根据题意可以知道 ,计算得出 ,所以 ,又因为是减函数 ,所以
.此时 也是单调减的 ,且过点 .所以 A选项是正确的符合题意 .所以 A选
项是正确的 .
【方法规律】
1.识图常用的方法
(1)定性分析法:通过对问题进行 定性的分析,从而得出图象的上升 (或下降 )的趋势,利用这一特征分析解
决问题.
(2)定量计算法:通过定量的计算来分析解决问题.
(3)函数模型法:由所提供的图象特征,联想相关函数模型,利用这一函数模型来分析解决问题 .
( 4)利用函数本身的性能或特殊点(与 、 轴的交点,最高点、最低点等)进行排除验证 .
2.函数图象的识辨可从以下方面入手:
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位 置;
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的周期性,判断图象的循环往复.
利用上述方法,排除、筛选错误与正确的选项.
【解题技巧】
函数图象的分析判断主要依据两点:
一是根据函数的性质,如函数的奇偶性、单调性、值域、定义域等;
二是根据特殊点的函数值,采用排除的方法得出正确的选项.
【易错点睛】
1.函数图象左右平移平移的长度单位是加在 上,而不是加在 上,处理左右平移问题要注意平移方向与
平移的长度单位 .
2.在图象识别中忽视函数的定义域或有关性质分析不到位导致解题出错 .
例 已知定义域为 [0,1]上的函数 图象如下图左图所示,则函数 的图象可能是( )
【错解】先将 的图象沿 y轴对折得到 的图象,再将所得图象向左平移 1个长度单位就得到函数
的图象,故选 A.
【错因分析】没有掌握图象变换,图象平移长度单位是加在 上,而不是加在 上,本例因
= ,故先做对称变换后,应向右平移 1长度单位 .
【预防措施】先将所给函数化为 形式,若先做伸缩变换,再作平移变换,注意 平移方向和平移
单位 .
【正解】 因 = ,先将 的图象沿 y轴对折得到 的图象,再将所得图象向右平
移 1个长度单位就得到函数 的图象,故选 B.
热点 2 函数图象的应用
1.若函数 满足 ,当 x∈ [0, 1]时, ,若在区间 (-1, 1]上, 方程
有两个实数解,则实数 m的取值范围是 ( )
A. 0< m≤ B. 0< m< C. < m≤l D. < m< 1
【答案】
【解析】 有两个零点,即曲线 有两个交点 .
令 ,则 ,所以 .
在同一坐标系中,画出 的图象(如图所示):直线 过定点 ,所
以, 满足 即 选 .
2.( 2020·梅河口市第五中学高三) 已知函数 ( ,且 )在区间
上为单调函数,若函数 有两个不同的零点,则实数 的取值范围 是( )
A. B.
C. D.
【答案】 C
【解析】 因为函数 在区间 上为单调函数,且 在 上为单调递增函数,所以 在
上也为单调递增函数,因为 在 上为单调递减函数,所以 ,且
,即 ,所以 ,若函数 有两个不同的零点,则
函数 的图象与直线 有两个不同的交点,作出函数 的图象与直线 ,
如图:
由图可知,当 ,即 时,符合题意;当 ,即 时,直线 与抛物线
相切,联立直线 与抛物线 ,消去 得 ,所
以 ,解得 ,符合 .综上所述:实数 的取值范围是 .
3.设函数 ,若 在区间 上的值域为 ,则实数 的取
值范围为 __________.
【答案】
【解析】 由题意,可以考虑采用数形结合法,作出函数 的图象,当 时,函数
单调递减,且最小值为 ,则令 ,解得 ,当 时,函数
在 上单调递增,在 上单调递减,则最大 值为 2,且 , ,综上得所
求实数 的取值为 .
【方法规律】
1.研究函数的性质时一般要借助函数图象,体现了数形结合思想.
2.有些不等式问题常转化为两函数图象的上、下关系来解.
3.方程解的个数常转化为两熟悉的函数图象的交点个数问题来求解.
【解题技巧】
1.为了 更好的利用函数图象解题,准确的作出 函数的 图象 是解题关键 , 要准确的作出图象 必须做到以下两
点 :
(1)熟练掌握几种基本函数的图象,如二次函数、反比例函数、指数 函数、对数函数、幂函数、形如
的函数;
(2)掌握平移变换、伸缩变换、对称变换、翻折变换、周期变换等常用的方法技巧,来帮助我们简化作图过
程 .
2. 利用函数的图象研究函数的性质
从图象的最高点、最低点,分析函数的最值、极值;从图象的对称性,分析函数的奇偶性;从图象的走向
趋势,分析函数的单调性、周期性等.
3.利用函数的图象研究方程根的 分布或求根 的近似解
对所给的方程进行变形, 转化为两个熟悉的函数的交点 问题,作出这两个函数的图象,观察出交点个数即
为方程解的个数,或找出解所在的区间或结合图象 由解的个数 找出 参数 满足的条件,从而求出参数的范围
或参数的 值.
【易错点睛】
一个函数的图象关于原点 (y轴 )对称与两个函数的图象关于原点 (y轴 )对称不同,前者是自身对称,且为奇
(偶 )函数,后者是两个不同的函数对称.
例 已知函数 的定义域为 R,则函数 与函数 的图象关于( )
A.直线 =0对称 B.直线 =0对称 C.直线 对称 D.直线 =2对称
【错解】∵函数定义在实数集上,且 ,
∴函数 的图象关于直线 =0对称,故选 B.
【错因分析】错用函数自身对称的结论处理两个函数对称问题 .
【预防措施】首先分析要解决的对称问题是自身的对称问题还是两个函数的对称问题,其次要掌握判断函
数自身对称的方法和判断两个函数对称的方法 .
【正解】函数 的图象是将函数 的图象向右平移 2个单位得到,
而函数 = 的图象是先将 的图象关于 =0对称变换得到 的图
象,再将 的图象向右平移 2个单位得到,因此函数 与函数 关于 =2
对称,故选 D.
【 热点 预测 】
1.( 2020·天津高三二模) 函数 的部分图象大致为( )
A. B. C. D.
【答案】 A
【解析】 令 ,则 ,
为奇函数 .又因为 为偶函数, 的定义域为 ,
故 为奇函数,排除 B, C.因为 ,
,排除 D., 故选: A
2.已知函数 对任意的 有 ,且当 时, ,则函数 的
大致图象为( )
【答案】 D
【解析】 故函数为奇函数,根据 图象,选 D.
3. 甲从 A地到 B地,途中前一半路程的行驶速度是 ,后半路程的行驶速度是 ,则表示甲从 A
地到 B地走过的路程 s与时间 t的关系的图象 为( )
A. B. C. D.
【答案】 B
【解析】 ∵ , ∴ 前一半路程耗时多,后一半路程耗时少, B选项正确 .故选: B
4.已知函数 , 是定义在 R上的奇函数,当 时, ,则函数
的大致图象为
【答案】 D
【解析】由 是偶函数, 是奇函数,所以 是奇函数,图像关于原点对称,排除 A,B,
当 时 ,所以 D正确 .
5.偶函数 满足 ,且在 时, ,则关于 的方程 在
上的根的个数是
A. 3 B. 4 C. 5 D. 6
【答案】
【解析】 由 题意可得, .即函数 为周期为 的周期函数,又 是偶函数,
所以,在同一坐标系内,画出函数 , 的图象,观察它们在区间 的交点个数,就是方
程 在 上根的个数,结合函数图象的对称性,共有 个交点, 故选 .
6.( 2020·重庆八中高三) 已知函数 ,则下列结论正确的是( )
A. B. 函数 有 5个零点
C. 函数 在 上单调递增 D. 函数 的值域为
【答案】 C
【解析】 因为 ,所以 ,
,故 A错误;当 时, ,
当 时, ,所以画出函数图象如下所示,由图可得函数有 4
个零点,故 B错误,函数在 上单调递增,故 C正确; ,
,故函数的值域为 ,故 D错误;故选: C
7.已知函数 ,则函数 的大致图象是( )
y y y y
O x O x O x O x
A B C D
【答案】 D
【解析】因为函数 ,所以 ,故函数 仍
是分段函数 ,以 为界分段 ,且在 上递减,只有 D符合,故选 D.
8.( 2020·巩义市教育科研培训中心高三) 设 、 、 依次表示函数 , ,
的零点,则 、 、 的大小关系为( ).
A. B. C. D.
【答案】 D
【解析】 依题意可得, 的图象与 的图象交点的横坐标为 ,
作出图象如图:
由图象可知, ,
9.已知函数 f( x) = , 若关于 x的方程 f( f( x)) =a存在 2个实数根,则 a的取值范围为
( )
A. [﹣ 24, 0) B. (﹣ ∞ ,﹣ 24) ∪[0 , 2) C. (﹣ 24, 3) D. (﹣ ∞ ,﹣ 24]∪[0 , 2]
【答案】 B
【解析】 画出 y=f(x)的图像,如下图,令 t=f(x),则 f(t)=a,现在要有 2个实根, f(t)=a有 0, 1,2个解三
种情况 .当 a>3时, f(t)=a有 0个解,不符 ; 当 时, f(t)=a有 1个解, ,当
时, t=f(x)有两解,此时 ; 当 时, f(t)=a有 2个解, 或 , 和
总共有两个实数解,当一个是两个解,一个为 0个解时, ,此时 ,符合。当两个均为一个解
时 , 显然不符 .综上所述 (﹣ ∞ ,﹣ 24)∪ [0, 2) ,选 B.
,
10.已知函数 其中 表示不超过 的最大整数,(如 , , ) .
若直线 与函数 的图象恰有三个不同的交点,则实数 的取值范围是( )
A. B. C. D.
【答案】 B
【解析】由题意,函数 是周期为 1的周期函数,在 时, ,其图象如图所示,直线
过点 ,由于 ,符合题意的直线必定在点 正方,在点 上方(可过点
), , ,故有 .
11.( 2020·河南省高 三 ) 定义在 上的函数 满足 与 ,且当
时, ,则函数 的零点个数为( )
A. 12 B. 10 C. 8 D. 6
【答案】 C
【解析】 因为 ,令 ,得 ,所以函数 是定义在 上的偶
函数.又因为 ,得 ,所以函数 是周期为 2的周期函数.
由 ,得 ,由换底公式,得 ,即 ,
因此,求函数 的零点个数,即可以转化为求函数 与
的图象的交点个数.另外,函数 的周期为 2,得
;由 且 ,得 , 1, 2,所以函数 的 定义域是 ,
函数 的定义域是 .在同一坐标系中作出函数 与
的图象(如图所示),
由图可知,函数 与 的图象一共有 8个交点.
即函数 的零点个数为 8.
12.已知函数 ,若关于 x的方程 有 8个不等的
实数根,则 a的取值范围是( )
A. B. C. ( 1, 2) D.
【答案】 D
【解析】 画出 y=f(x)的图像,如下图,令 t=f(x),方程变形为 ,因为有 8个不等的实数根,
所以 ,令 = ,所以 ,解得
13.已知函数 则函数 的零点个数为 个.
【答案 】
【解析】 的零点个数,即是方程 的根的个数,也就是 与 的
图象的交点个数,分别作出 与 的图象,如图所示,由图象知 与 的图象
有两个交点,所以函数 有 个零点 .
14.若存在 使得不等式 成立,则实数 的取值范围是 .
【答案】 .
【解析】原不等式等价于: ,
故问题等价于 , ,设 , ,
∴ , ,∴实数 的取值范围是 .
15.已知函数 ,则函数 零点的个数为 __________.
【答案】 3
【解析】
设 ,则 , 由 ,得 , 画出 与 的图象 , 如
图可知 轴左边有 个交点 ,又 , 可知 轴右侧区间 各有 个交点,
共有 个交点 , 即方程 有 个解, , 也有 个解,函数 有 个零点,故
答案为 .
16.已知函数 ,设 ,若 ,则 的取值范围是 .
【答案】 .
【解析】 由函数 ,作出其图象如 下 图,因为函数 在 和 上都是
单调函数,所以,若满足 时 , ,必有 , ,由图可知,使
的 , , 由不等式的可乘积性得: , 故答案为 .
17.已知函数 ,则方程 恰有两个不同实数根时,实数 的取值范围
是 .
【答案】
【解析】∵方程 恰有两个不同实数根,∴ 与 有 2个交点,∵ 表示直线
的斜率,∴ ,设切点为 , ,所以切线方程为 ,而切线过原点,
所以 , , ,所以直线 的斜率为 ,直线 与 平行,所以直线 的斜率
为 ,所以当直线在 和 之间时 ,符合题意,所以实数 的取值范围是 ,还有一部分是在 的位
置向下旋转一直到转平为止都符合题意,这时实数 的取值范围是 ,所以综上所述,实数 的取值
范围是 .
18. 已知 若关于 的方程 有四个实根 , 则四根之和
的取值范 围 _________
【答案】
【解析】 设 ,则有图得
从而 .
1.最新考试说明:
① 在实际情境中,会根据不同的需要选择图象法、列表法、解析法表示函数.
【 2020年高考北京卷 15】 为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达
标的企业要限期整改.设企业的污水排放量 与时间 的关系为 ,用 的大小评
价在 这段时间内企业污水治理能力的强弱. 已知整改期内,甲、乙两企业的污水排放量与时间的关
系如下图所示.
给出下列四个结论 :
① 在 这段时间内 , 甲企业的污水治理能力比乙企 业强 ;
②在 时刻,甲企业的污水治理能力比乙企业强;
③ 在 时刻 , 甲 、 乙两企业的污水排放量都已达标 ;
④ 甲企业在 , , 这三段时间中 , 在 的污水治理能力最强.
其中所有正确结论的 序号是 .
【答案】 ①②③
【解析】∵ 用 来评价治污能力 ,而 是图像上两点连线的斜率 ,在
上 , 甲的治污能力比乙强 , 故 ①对, 时刻甲比乙强 , 时刻都低于达标排放量 ,∴都达标,甲企业在
时刻治污能力不是最强 .
【专家解读】本题的特点是注重 知识的灵活运用 ,本题考查了 函数图象及其性质的综合应用 ,考 查 数形结
合思想 ,考查数学运算 、数学直观、逻辑推理等 学科素养.解题关键是正确 接函数的图像及其性质解决问
题.
【 2020年高考天津卷 3】 函数 的图象大致为( )
A. B.
C. D.
【答案】 A
【思路导引】 由题意首先确定函数的奇偶性,然后考查函数在特殊点的函数值排除错误选项即可确定函数
的图象 .
【解析】 由函数的解析式可得: ,则函数 为奇函数,其图象关于坐标原点
对称,选项 CD错误;当 时, ,选项 B错误 . 故选 A.
【专家解读】本题的特点是 函数图象及其性质的应用 ,本题考查了 函数图象的识别 ,考查 数 形结合思想 ,
考查数学运算 、数学直观等 学科素养.解题关键是 观察函数图象,结合排除法解决问题.
【方法总结】 函数图象的识辨可从以下方面入手: (1)从函数的定义域,判断图象的左右位置;从函数的值
域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势. (3)从函数的奇偶性,判断图象的对
称性. (4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.
② 会运用函数图象理解和研究函数的性质,解决方程解的个数与不等式的解的问题.
【 2020年高考北京卷 6】 已知函数 ,则不等式 的解集是 ( )
A. B. C. D.
【答案】 C
【解析】 不等式 化为 在同一直角坐标系下作出 y=2x, y=x+1的图象(如图),得 不等式
的解集是 , 故选 C.
【专家解读】本题考查了 简单指数 不等式的解法,考查 数形结合思想 ,考查数学运算 、数学直观 学科素养.解
题关键是正确 作出函数图象,利用图象解决问题.
【 2020年高考浙江卷 9】 已知 且 ,若 在 上恒成立,则
( )
A. B. C. D.
【答案】 C
【思路导引】 对 分 与 两种情况讨论,结合三次函数的性质分 析即可得到答案 .
【解析】 当 时,在 上, 恒成立,∴只需满足 恒成立,此时
,由二次函数的图象可知,只有 时,满足 , 不满条件;
当 时,在 上, 恒成立,∴只需满足 恒成立,此时当两根分别
为 和 ,
( 1)当 时,此时 ,当 时, 不恒成立,
( 2)当 时,此时 ,若满足 恒成立,只需满足
当 时,此时 ,满足 恒成立,
综上可知满足 在 恒成立时,只有 ,故选 C .
【专家解读】本题的特点是 知识的灵活运用 ,本题考查了三次函数在给定区间上恒成立问题,考查 数形结
合及 分类讨论思想,考查 数学运算 、数学直观、逻辑推理等 学科素养.解题关键是 合理分类,做到不重不
漏.
③ 会用数形结合思想、转化与化归思想解决数学问题 .
【 2020 年高考上海卷 11】 已知 , 若存在定义域为 的函数 同时满足下列两个条件 ,①对任意
, 的值为 或 ;②关于 的方程 无实数解 ; 则 的取值范围为 .
【答案】
【解析】由 和 的图象和函数的定义可知,若满足 的值为 或 ,只有
, ,结合②可知若方程 无实数解,则 ,
故答案为: .
【专家解读】本题的特点是 函数图象及其性质的应用 ,本题考查了 函数与方程 ,二次函数图象及其应用 ,
考查 函数与方程思想、数形结合思想 ,考查数学运算 、数学直观、数学建模等 学科素养.解题关键是正确
作出函数图象,应用函数图象及其性质解决问题.
【 2020年高考天津卷 9】 已知函数 若函数 恰有 4个
零点,则 的取值范围是( )
A. B.
C. D.
【答案】 D
【思路导引】 由 ,结合已知,将问题转化为 与 有 个不同交点,分
三种情况,数形结合讨论即可得到答案 .
【解析】 注意到 ,所以要使 恰有 4个零点,只需方程 恰有 3个实根 , 即可,
令 ,即 与 的图象有 个不同交点 . 因为 ,
当 时,此时 ,如图 1, 与 有 个不同交点,不满足题意;当 时,如图
2,此时 与 恒有 个不同交点,满足题意;当 时,如图 3,当 与
相切时,联立方程得 ,令 得 ,解得 (负值舍去),所以 .
综上, 的取值范围为 , 故选 D.
【专家解读】本题的特点是 函数图象及其现在的灵活运用 ,本题考查了 函数与方程的应用,考查数形结合 、
分类讨论、 转化与化归 等数学 思想 方法 ,考查数学运算 、直观想象、数学建模等 学科素养.解题关键是正
确 作出函数图象,应用函数图象及其性质解 决问题.
2.命题方向预测:
从近 二 年的高考试题来看,主要考查图象的辨识以及利用图象研究函数的性质、方程 及 不等式的解,多以
选择题 、填空题 的形式出现,属中低档题,主要考查基本初等函数的图象及应用 .
预测 2017年高考对本节内容的考查仍将以 函数图象识别与 函数图象的应用为主, 依然体现“有图考图”“无
图考图”的原则, 题型 仍为 选择题 或填空题 的形式.备考时要求熟练掌握各种基本初等函数的图象及性质,
加强函数性质的应用意识,另外还应熟练掌握各种图象变换的法则 .
3.课本结论总结:
( 1) 画函数图象的一般方法
①描点法 :当函 数表达式 (或变形后的表达式 )是熟悉的基本函数时,就可根据这些函数的特征直接作出 ,
其步骤为: 先确定函数的定义域,化简给定的函数解析式,再根据化简后的函数解析式研究函数的值域、
单调性、奇偶性、对称性、极值、最值,再根据函数的特点取值、列表,描点,连线,注意取点,一定要
包括关键点,如极值点、与 轴的交点等.
② 图象变换法:若函数图象可由某个基本函数的图象经过平移、翻折、对称得到,可利用图象变换作出,
但要注意变换顺序,对不能直接找到熟悉的基本函数的要先变形,并应注意 平移变换与伸缩变换的顺序对
变换单位及解析式的影响.
( 2)常见的图象变换
①平移变换:
左右平移: 函数 的图象可由函数 的图象向左( +)或向右( — )平移 个单位
得到;
上下平移: ( )的图象可由函数 的图象向上( +) 或向下( — )平移 个单位
得到;
②伸缩变换
函数 是将函数 图象上各点的纵坐标不变,横坐标变为原来的 得到;
函数 是将函数 图象上各点的横坐标不变,纵坐标变为原来的 A倍的得到;
③对称变换
函数 图象关于 轴对称得到函数 图象;
函数 图象关于 轴对称得到函数 图象;
函数 图象关于原点对称得到函数 图象;
函数 图象关于直线 对称得到函数为 图象.
④翻折变换
函数 的图象这样得到:函数 在 轴右侧的图象保持不变,左侧的图象去掉后,再将右
侧的图象翻折到 轴左侧(函数 为偶函数,其图象关于 轴对称) ;
函数 的图象是这样得到的:函数 在 轴上方的图象保持不变,把下方的图象关于 轴
对称到上方(注意到函数 的函数值都大于零).
4.名师二级结 论:
( 1)函数图象的几个应用
①判断函数的奇偶性、确定单调区间:图象关于原点对称是奇函数,图象关于 y轴对称是偶函数 .图象从左
到右上升段对应的 的取值范围是增区间,下降对应的 的取值范围 是减区间 .
②方程 的根就是函数 与函数 图象交点的横坐标 .
③不等式 的解集是函数 的图象在函数 图象上方的一段对应的 的取值范围
(交点坐标要通过解方程求得)
( 2)函数 的图象的 对称性
①若函数 关于 对称 对定义域内任意 都有 = 对定义域内任意 都
有 = 是偶函数;
②函数 关于点( , 0)对称 对定义域内任意 都有 =- =-
是奇函数;
③若 函数 对定义域内任意 都有 ,则 函数 的对称轴是 ;
④若 函数 对定义域内任意 都有 ,则 函数 的对称轴中心为 ;
⑤ 函数 关于 对称 .
(3) 明确函数图象形状和位置的方法大致有以下三种途径.
① 图象变换:平移变换、伸缩变换、对称变换.
② 函数解析式的等价变换.
③ 研究函数的性质.
5.课本经典习题:
(1)新课标 A版第 23 页,练习第 2 题
下图中哪几个图象与下述三个事件分别吻合的最好?请你为剩下的那个图象写出一个事件 .
(1) 我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到作业本在上学;
(2) 我骑车一路匀速行驶,只是在途中遇到一次交通堵塞,耽误了一些时间;
(3) 我出发后,心情轻松,缓缓前进,后来为了赶时间开始加速 .
【经典理由】本题主要考查了图象识别,与高考题中的图象识别题很类似
(2) 新课标 A版第 25 页,习题 1.2 B组第 1 题
函数 的图象如图所示(图中曲线 与直线 无限接近,但永不相交) .
①函数 的定义域是什么?
②函数 的值域是什么?
③ 取何值时,只有唯一的 与之对应?
【经典理由】本题主要考查了图象应用,与高考题中的图象识应用很类似
6.考点交汇展示:
(1)与参数范围问 题交汇
【例】 ( 2020·甘肃省静宁县第一中学高三) 已知函数 ,若函数
有 4个零点,则实数 的取值范围是 ( )
A. B.
C. D.
【答案】 B
【解析】 函数 ,函数 有 4个零点,即 有四个不同
交点 .画出函数 图像如下图所示:
由图可知,当 时,设对应二次函数顶点为 ,则 , ,当 时,设
对应二次函数的顶点为 ,则 , .所以 .当直线 与 时的
函数图像相切时与函数 图像有三个交点,此时 ,化简可得 .
,解得 (舍);当直线 与 时的函数图
像相切时与函数 图像有五个交点,此时 , 化简可得 .
,解得 (舍);故当 有四个不同交点时
.
【例 2】 函数 的图象如图所示,则下列结论成立的是( )
( A) , , ( B) , ,
( C) , , ( D) , ,
【答案】 C
【解析】 由 及图象可知, , ,则 ;当 时, ,所以
;当 , ,所以 ,所以 .故 , , ,选 C.
(2)与函数性质交汇
【例】 ( 2020·陕西省西安中学高 三 ) 已知定义在 R上的函数 对任意的 x都满足 ,
当 时, .若函数 恰有 6个不同零点,则 a的取值范围是( )
A. B. C. D.
【答案】 A
【解析】 由条件可知函数 恰有 6个不同的零点,转化为 与 恰
有 6个不同的交点, , 的周期 ,且 时, ,
是偶函数,图象关于 轴对称,如图,在同一坐标系下画出函数 和 的图
象, ① 当 时, 的图象如图所示, 轴左侧有 4个交点,右侧有 2个交点,
此时应满足 ,解得 ;
② 当 时, 与 在 轴左侧有 2个交点,右侧有 4个交点,
此时应满足 ,解得: ;综上可知, 的取值范围是 .
【例 4】 在同一直坐标系中,一次函数 与二次函数 的图像可能是( )
A. B.
C. D.
【答案】 B
【解析】 因为直线 恒过点( 0, 1),所以舍去 A; 二次函数 开口向上,所以舍去 C;当
时,二次函数 顶点在 x轴上方,所以舍去 D,选 B.
(3)与函数零点问题交汇
【例 5】已知 是定义在 上的奇函数 , 且 ,则函数 的
零点个数为 ( )
A. B. C. D.
【答案】 D
【解析】 由 ,得 ,函数 的
零点,即方程 的根,也就是函数 与 交点的横坐标,结合函数
为实数集上的奇函数,作出图象如图,由图可知,函数 的零点个数 个.
故选 D.
( 4)与不等式交汇
【例 6】 ( 2019·定远县育才学校高 三) 已知函数 ,若不等式 恒成
立,则实数 的取值范围是( )
A. B. C. D.
【答案】 D
【解析】 画出函数 f( x) 的图象 ,
由 y= 可得直线在 y轴上的截距为 4, 若 4 恒成立 , 图像恒在分段函数的上
方,故
【例 7】 若 ,则 的取值范围是( )
A. B. C. D.
【答案】 C
【解析】
设 ,联立 得 ,因为 ,所以 ,
由它们的图象可知 的取值范围是 .
( 5)与方程交汇
【例 8】( 2020·浙江省高 三 ) 已知函数 ,若关于 的方程
有且仅有三个不同的整数解,则实数 的取值范围是( )
A. B. C. D.
【答案】 A
【解析】 , 函数 位于直线
和 的图象上有三个横坐标为整数的点 .当 时, 且 ,
由双勾函数的单调性可知,函数 在区间 上单调递减,在区间 上单调递增,
当 时, , , , , ,
且 ,如下图所示:要使得函数 位于直线 和 的图象上有
三个横坐标为整数的点,则 ,即 ,解得 .
因此,实数 的取值范围是 .
【 考点分类 】
热点 1 函数图象的识别
1.( 2020·四川省仁寿一中高三) 函数 图象的大致形状是( )
A. B. C. D.
【答案】 B
【解析】 ,
,故 为奇函数,排除选项 A、 C;又 ,排除 D,选 B.
2.( 2020·河北省衡水中学高三三模) 如图,是函数 的部分图象,则 的解析式可能是( )
A. B.
C. D.
【答案】 B
【解析】 由图像可知,函数图像关于 轴对称,所以 应为偶函数,所以排除 A;由图像可知函数值能
取到小于 0的值,所以排除 C;对于当 时, ,而当
时, ,而正弦的函数图像可知 D不正确 ,
3.若函数 ( 且 )过定点 ,且 在定义域 上是减函数,则
的图象是( )
A. B. C. D.
【答案】 A
【解析 】 根据题意可以知道 ,计算得出 ,所以 ,又因为是减函数 ,所以
.此时 也是单调减的 ,且过点 .所以 A选项是正确的符合题意 .所以 A选
项是正确的 .
【方法规律】
1.识图常用的方法
(1)定性分析法:通过对问题进行 定性的分析,从而得出图象的上升 (或下降 )的趋势,利用这一特征分析解
决问题.
(2)定量计算法:通过定量的计算来分析解决问题.
(3)函数模型法:由所提供的图象特征,联想相关函数模型,利用这一函数模型来分析解决问题 .
( 4)利用函数本身的性能或特殊点(与 、 轴的交点,最高点、最低点等)进行排除验证 .
2.函数图象的识辨可从以下方面入手:
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位 置;
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的周期性,判断图象的循环往复.
利用上述方法,排除、筛选错误与正确的选项.
【解题技巧】
函数图象的分析判断主要依据两点:
一是根据函数的性质,如函数的奇偶性、单调性、值域、定义域等;
二是根据特殊点的函数值,采用排除的方法得出正确的选项.
【易错点睛】
1.函数图象左右平移平移的长度单位是加在 上,而不是加在 上,处理左右平移问题要注意平移方向与
平移的长度单位 .
2.在图象识别中忽视函数的定义域或有关性质分析不到位导致解题出错 .
例 已知定义域为 [0,1]上的函数 图象如下图左图所示,则函数 的图象可能是( )
【错解】先将 的图象沿 y轴对折得到 的图象,再将所得图象向左平移 1个长度单位就得到函数
的图象,故选 A.
【错因分析】没有掌握图象变换,图象平移长度单位是加在 上,而不是加在 上,本例因
= ,故先做对称变换后,应向右平移 1长度单位 .
【预防措施】先将所给函数化为 形式,若先做伸缩变换,再作平移变换,注意 平移方向和平移
单位 .
【正解】 因 = ,先将 的图象沿 y轴对折得到 的图象,再将所得图象向右平
移 1个长度单位就得到函数 的图象,故选 B.
热点 2 函数图象的应用
1.若函数 满足 ,当 x∈ [0, 1]时, ,若在区间 (-1, 1]上, 方程
有两个实数解,则实数 m的取值范围是 ( )
A. 0< m≤ B. 0< m< C. < m≤l D. < m< 1
【答案】
【解析】 有两个零点,即曲线 有两个交点 .
令 ,则 ,所以 .
在同一坐标系中,画出 的图象(如图所示):直线 过定点 ,所
以, 满足 即 选 .
2.( 2020·梅河口市第五中学高三) 已知函数 ( ,且 )在区间
上为单调函数,若函数 有两个不同的零点,则实数 的取值范围 是( )
A. B.
C. D.
【答案】 C
【解析】 因为函数 在区间 上为单调函数,且 在 上为单调递增函数,所以 在
上也为单调递增函数,因为 在 上为单调递减函数,所以 ,且
,即 ,所以 ,若函数 有两个不同的零点,则
函数 的图象与直线 有两个不同的交点,作出函数 的图象与直线 ,
如图:
由图可知,当 ,即 时,符合题意;当 ,即 时,直线 与抛物线
相切,联立直线 与抛物线 ,消去 得 ,所
以 ,解得 ,符合 .综上所述:实数 的取值范围是 .
3.设函数 ,若 在区间 上的值域为 ,则实数 的取
值范围为 __________.
【答案】
【解析】 由题意,可以考虑采用数形结合法,作出函数 的图象,当 时,函数
单调递减,且最小值为 ,则令 ,解得 ,当 时,函数
在 上单调递增,在 上单调递减,则最大 值为 2,且 , ,综上得所
求实数 的取值为 .
【方法规律】
1.研究函数的性质时一般要借助函数图象,体现了数形结合思想.
2.有些不等式问题常转化为两函数图象的上、下关系来解.
3.方程解的个数常转化为两熟悉的函数图象的交点个数问题来求解.
【解题技巧】
1.为了 更好的利用函数图象解题,准确的作出 函数的 图象 是解题关键 , 要准确的作出图象 必须做到以下两
点 :
(1)熟练掌握几种基本函数的图象,如二次函数、反比例函数、指数 函数、对数函数、幂函数、形如
的函数;
(2)掌握平移变换、伸缩变换、对称变换、翻折变换、周期变换等常用的方法技巧,来帮助我们简化作图过
程 .
2. 利用函数的图象研究函数的性质
从图象的最高点、最低点,分析函数的最值、极值;从图象的对称性,分析函数的奇偶性;从图象的走向
趋势,分析函数的单调性、周期性等.
3.利用函数的图象研究方程根的 分布或求根 的近似解
对所给的方程进行变形, 转化为两个熟悉的函数的交点 问题,作出这两个函数的图象,观察出交点个数即
为方程解的个数,或找出解所在的区间或结合图象 由解的个数 找出 参数 满足的条件,从而求出参数的范围
或参数的 值.
【易错点睛】
一个函数的图象关于原点 (y轴 )对称与两个函数的图象关于原点 (y轴 )对称不同,前者是自身对称,且为奇
(偶 )函数,后者是两个不同的函数对称.
例 已知函数 的定义域为 R,则函数 与函数 的图象关于( )
A.直线 =0对称 B.直线 =0对称 C.直线 对称 D.直线 =2对称
【错解】∵函数定义在实数集上,且 ,
∴函数 的图象关于直线 =0对称,故选 B.
【错因分析】错用函数自身对称的结论处理两个函数对称问题 .
【预防措施】首先分析要解决的对称问题是自身的对称问题还是两个函数的对称问题,其次要掌握判断函
数自身对称的方法和判断两个函数对称的方法 .
【正解】函数 的图象是将函数 的图象向右平移 2个单位得到,
而函数 = 的图象是先将 的图象关于 =0对称变换得到 的图
象,再将 的图象向右平移 2个单位得到,因此函数 与函数 关于 =2
对称,故选 D.
【 热点 预测 】
1.( 2020·天津高三二模) 函数 的部分图象大致为( )
A. B. C. D.
【答案】 A
【解析】 令 ,则 ,
为奇函数 .又因为 为偶函数, 的定义域为 ,
故 为奇函数,排除 B, C.因为 ,
,排除 D., 故选: A
2.已知函数 对任意的 有 ,且当 时, ,则函数 的
大致图象为( )
【答案】 D
【解析】 故函数为奇函数,根据 图象,选 D.
3. 甲从 A地到 B地,途中前一半路程的行驶速度是 ,后半路程的行驶速度是 ,则表示甲从 A
地到 B地走过的路程 s与时间 t的关系的图象 为( )
A. B. C. D.
【答案】 B
【解析】 ∵ , ∴ 前一半路程耗时多,后一半路程耗时少, B选项正确 .故选: B
4.已知函数 , 是定义在 R上的奇函数,当 时, ,则函数
的大致图象为
【答案】 D
【解析】由 是偶函数, 是奇函数,所以 是奇函数,图像关于原点对称,排除 A,B,
当 时 ,所以 D正确 .
5.偶函数 满足 ,且在 时, ,则关于 的方程 在
上的根的个数是
A. 3 B. 4 C. 5 D. 6
【答案】
【解析】 由 题意可得, .即函数 为周期为 的周期函数,又 是偶函数,
所以,在同一坐标系内,画出函数 , 的图象,观察它们在区间 的交点个数,就是方
程 在 上根的个数,结合函数图象的对称性,共有 个交点, 故选 .
6.( 2020·重庆八中高三) 已知函数 ,则下列结论正确的是( )
A. B. 函数 有 5个零点
C. 函数 在 上单调递增 D. 函数 的值域为
【答案】 C
【解析】 因为 ,所以 ,
,故 A错误;当 时, ,
当 时, ,所以画出函数图象如下所示,由图可得函数有 4
个零点,故 B错误,函数在 上单调递增,故 C正确; ,
,故函数的值域为 ,故 D错误;故选: C
7.已知函数 ,则函数 的大致图象是( )
y y y y
O x O x O x O x
A B C D
【答案】 D
【解析】因为函数 ,所以 ,故函数 仍
是分段函数 ,以 为界分段 ,且在 上递减,只有 D符合,故选 D.
8.( 2020·巩义市教育科研培训中心高三) 设 、 、 依次表示函数 , ,
的零点,则 、 、 的大小关系为( ).
A. B. C. D.
【答案】 D
【解析】 依题意可得, 的图象与 的图象交点的横坐标为 ,
作出图象如图:
由图象可知, ,
9.已知函数 f( x) = , 若关于 x的方程 f( f( x)) =a存在 2个实数根,则 a的取值范围为
( )
A. [﹣ 24, 0) B. (﹣ ∞ ,﹣ 24) ∪[0 , 2) C. (﹣ 24, 3) D. (﹣ ∞ ,﹣ 24]∪[0 , 2]
【答案】 B
【解析】 画出 y=f(x)的图像,如下图,令 t=f(x),则 f(t)=a,现在要有 2个实根, f(t)=a有 0, 1,2个解三
种情况 .当 a>3时, f(t)=a有 0个解,不符 ; 当 时, f(t)=a有 1个解, ,当
时, t=f(x)有两解,此时 ; 当 时, f(t)=a有 2个解, 或 , 和
总共有两个实数解,当一个是两个解,一个为 0个解时, ,此时 ,符合。当两个均为一个解
时 , 显然不符 .综上所述 (﹣ ∞ ,﹣ 24)∪ [0, 2) ,选 B.
,
10.已知函数 其中 表示不超过 的最大整数,(如 , , ) .
若直线 与函数 的图象恰有三个不同的交点,则实数 的取值范围是( )
A. B. C. D.
【答案】 B
【解析】由题意,函数 是周期为 1的周期函数,在 时, ,其图象如图所示,直线
过点 ,由于 ,符合题意的直线必定在点 正方,在点 上方(可过点
), , ,故有 .
11.( 2020·河南省高 三 ) 定义在 上的函数 满足 与 ,且当
时, ,则函数 的零点个数为( )
A. 12 B. 10 C. 8 D. 6
【答案】 C
【解析】 因为 ,令 ,得 ,所以函数 是定义在 上的偶
函数.又因为 ,得 ,所以函数 是周期为 2的周期函数.
由 ,得 ,由换底公式,得 ,即 ,
因此,求函数 的零点个数,即可以转化为求函数 与
的图象的交点个数.另外,函数 的周期为 2,得
;由 且 ,得 , 1, 2,所以函数 的 定义域是 ,
函数 的定义域是 .在同一坐标系中作出函数 与
的图象(如图所示),
由图可知,函数 与 的图象一共有 8个交点.
即函数 的零点个数为 8.
12.已知函数 ,若关于 x的方程 有 8个不等的
实数根,则 a的取值范围是( )
A. B. C. ( 1, 2) D.
【答案】 D
【解析】 画出 y=f(x)的图像,如下图,令 t=f(x),方程变形为 ,因为有 8个不等的实数根,
所以 ,令 = ,所以 ,解得
13.已知函数 则函数 的零点个数为 个.
【答案 】
【解析】 的零点个数,即是方程 的根的个数,也就是 与 的
图象的交点个数,分别作出 与 的图象,如图所示,由图象知 与 的图象
有两个交点,所以函数 有 个零点 .
14.若存在 使得不等式 成立,则实数 的取值范围是 .
【答案】 .
【解析】原不等式等价于: ,
故问题等价于 , ,设 , ,
∴ , ,∴实数 的取值范围是 .
15.已知函数 ,则函数 零点的个数为 __________.
【答案】 3
【解析】
设 ,则 , 由 ,得 , 画出 与 的图象 , 如
图可知 轴左边有 个交点 ,又 , 可知 轴右侧区间 各有 个交点,
共有 个交点 , 即方程 有 个解, , 也有 个解,函数 有 个零点,故
答案为 .
16.已知函数 ,设 ,若 ,则 的取值范围是 .
【答案】 .
【解析】 由函数 ,作出其图象如 下 图,因为函数 在 和 上都是
单调函数,所以,若满足 时 , ,必有 , ,由图可知,使
的 , , 由不等式的可乘积性得: , 故答案为 .
17.已知函数 ,则方程 恰有两个不同实数根时,实数 的取值范围
是 .
【答案】
【解析】∵方程 恰有两个不同实数根,∴ 与 有 2个交点,∵ 表示直线
的斜率,∴ ,设切点为 , ,所以切线方程为 ,而切线过原点,
所以 , , ,所以直线 的斜率为 ,直线 与 平行,所以直线 的斜率
为 ,所以当直线在 和 之间时 ,符合题意,所以实数 的取值范围是 ,还有一部分是在 的位
置向下旋转一直到转平为止都符合题意,这时实数 的取值范围是 ,所以综上所述,实数 的取值
范围是 .
18. 已知 若关于 的方程 有四个实根 , 则四根之和
的取值范 围 _________
【答案】
【解析】 设 ,则有图得
从而 .
