第二章 一元二次方程单元质量检测试卷 B(含答案)
文档属性
| 名称 | 第二章 一元二次方程单元质量检测试卷 B(含答案) |  | |
| 格式 | rar | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-19 16:23:22 | ||
图片预览




文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版2020-2021学年九年级(上)第二章一元二次方程检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;共36分)
1.
一元二次方程
的根为
A.
B.
,
C.
D.
2.
将一元二次方程
化成
(,
为常数)的形式,则
,
的值分别是
A.
,
B.
,
C.
,
D.
,
3.
一个两位数等于它的个位数的平方,且个位数字比十位数字大
,则这个两位数为
A.
B.
C.
或
D.
或
4.
青云超市某服装专柜在销售中发现:进货价为每件
元,销售价为每件
元的某品牌童装平均每天可售出
件.为了迎接"六一",商场决定采取适当的降价措施,扩大销售量,增加盈利.经调查发现:如果每件童装降价
元,那么平均每天就可多售出
件,要想平均每天销售这种童装盈利
元,同时又要使顾客得到较多的实惠,设降价
元,根据题意列方程得
.
A.
B.
C.
D.
5.
已知关于
的一元二次方程
有两个不相等的实数根
,.若
,则
的值是
A.
B.
C.
或
D.
不存在
6.
今年以来,CPI(居民消费价格总水平)的不断上涨已成为热门话题.已知某种食品在9月份的售价为
,11月份的售价为
.求这种食品平均每月上涨的百分率是多少?设这种食品平均每月上涨的百分率为
,根据题意可列方程式为
A.
B.
C.
D.
7.
方程(x-1)(x+3)=12化为ax2+bx+c=0的形式后,a,b,c的值分别为(
)
A.1,2,-15
B.1,-2,-15C.-1,-2,-15
D.-1,2,-15
8.
要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排
场比赛,则参赛球队有
A.
个
B.
个
C.
个
D.
个
9.
关于
的一元二次方程
的一个根是
,则
的值为
A.
B.
C.
或
D.
10.
已知关于
的方程
有两个不相等的实数根,若
,且方程的两个实数根都是整数,则
的值为
A.
B.
或
或
C.
D.
或
或
11.
一个等腰三角形的两边长分别是方程x2-7x+10=0的两根,则该等腰三角形的周长是(
)
A.12
B.9
C.13
D.12或9
12.
对于任意实数
,关于
的方程
的根的情况为
A.
有两个相等的实数根
B.
没有实数根
C.
有两个不相等的实数根
D.
无法判定
二、填空题(共6小题;共24分)
13.
()
?
;
()
?
.
14.
方程
的根是
?.
15.
方程
的根是
?.
16.
某校九年级学生毕业时,每个同学都将自己的相片向全班同学各送一张留作纪念,全班共送了
张相片,如果全班有
名学生,根据题意,列出方程为
?.
17.
如果关于
的一元二次方程
有两个不相等的实根,那么
的取值范围是
?.
18.
已知一个两位数,它的十位数字比个位数字小3,个位数字的平方恰好等于这个两位数,则这个两位数是___________.
三、解答题(共7小题;共60分)
19.
(8分)已知
是方程
的一个根,求
的值.
20.
(6分)
解方程:.
21.
(6分)解方程:.
22.
(8分)
有
个方程:;;;.小静同学解第
个方程
的步骤为:“①
;②
;③
;④
;⑤
;⑥
,.”
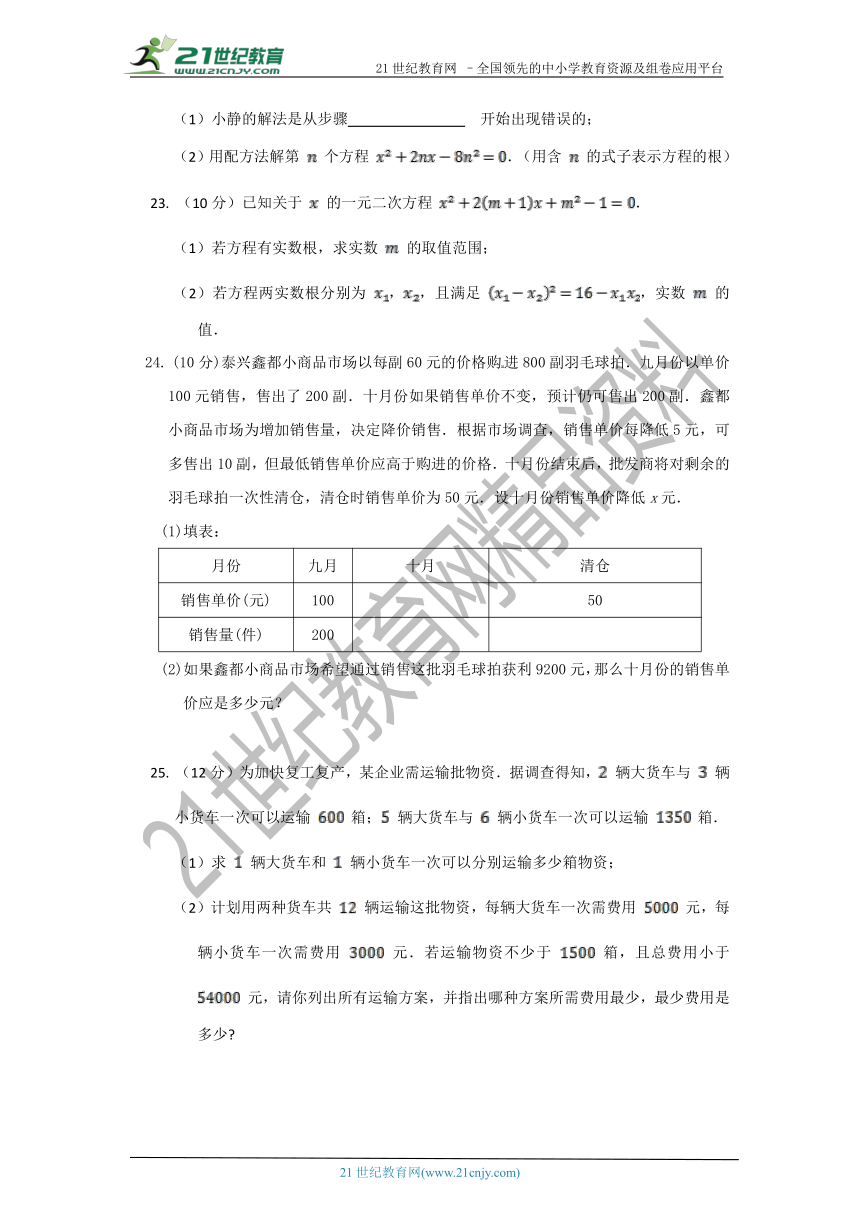
(1)小静的解法是从步骤
?
开始出现错误的;
(2)用配方法解第
个方程
.(用含
的式子表示方程的根)
23.
(10分)已知关于
的一元二次方程
.
(1)若方程有实数根,求实数
的取值范围;
(2)若方程两实数根分别为
,,且满足
,实数
的值.
24.
(10分)泰兴鑫都小商品市场以每副60元的价格购进800副羽毛球拍.九月份以单价100元销售,售出了200副.十月份如果销售单价不变,预计仍可售出200副.鑫都小商品市场为增加销售量,决定降价销售.根据市场调查,销售单价每降低5元,可多售出10副,但最低销售单价应高于购进的价格.十月份结束后,批发商将对剩余的羽毛球拍一次性清仓,清仓时销售单价为50元.设十月份销售单价降低x元.
(1)填表:
月份
九月
十月
清仓
销售单价(元)
100
50
销售量(件)
200
(2)如果鑫都小商品市场希望通过销售这批羽毛球拍获利9200元,那么十月份的销售单价应是多少元?
25.
(12分)为加快复工复产,某企业需运输批物资.据调查得知,
辆大货车与
辆小货车一次可以运输
箱;
辆大货车与
辆小货车一次可以运输
箱.
(1)求
辆大货车和
辆小货车一次可以分别运输多少箱物资;
(2)计划用两种货车共
辆运输这批物资,每辆大货车一次需费用
元,每辆小货车一次需费用
元.若运输物资不少于
箱,且总费用小于
元,请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?
答案
第一部分
1.
B
2.
A
3.
A
4.
A
5.
A
6.
B
7.
A
【解析】(1)如图1,,,
在
中,;
(2)如图2,,,
中,.
综上,蚂蚁从点
出发沿纸箱表面爬行到点
的最短距离是
.
8.
C
9.
B
10.
B
【解析】
关于
的方程
有两个不相等的实数根,
,
解得
,
方程的两个实数根都是整数,
是整数,
是完全平方数,
,
或
或
.
11.
若等腰三角形的三边为2,2,5,则2+2<5,不满足三角形三边关系,舍去.故选A.[]
12.
B
【解析】.
不论
为何值,,即
.
方程没有实数根.
第二部分
13.
,,,
14.
,
【解析】,
,
,
,.
15.
,
16.
17.
且
【解析】
关于
的一元二次方程
有两个不相等的实数根,
且
,即
,
解得:
且
.
18.
.25或36
第三部分
19.
是方程
的一个根,
.
即
.
20.
所以
21.
移项,得
即
则
所以
,.
22.
(1)
⑤
??????(2)
移项,得
配方,得
即
解得
即
所以
23.
(1)
根据题意可知,
解得
实数
的取值范围是
.
??????(2)
根据根与系数的关系可知
,.
,
,
即
.
,
解得
.
又
,
不合题意舍去,
.
24.
解:(1)100-x 200+2x 800-200-(200+2x)(3分)
(2)根据题意得100×200+(100-x)(200+2x)+50[800-200-(200+2x)]-60×800=9200,
解得x1=20,x2=-70(舍去).
当x=20时,100-x=80>60,符合题意.
答:十月份的销售单价应是80元.
25.
(1)
设
辆大货车和
辆小货车一次可以分别运输
箱,
箱物资,
根据题意,得:
解得:
答:
辆大货车和
辆小货车一次可以分别运输
箱,
箱物资.
??????(2)
设安排
辆大货车,则小货车
辆,总费用为
,
则
,
解得:,
而
,
解得:,
则
,
则运输方案有
种:
辆大货车和
辆小货车;
辆大货车和
辆小货车;
辆大货车和
辆小货车;
,
当
时,总费用最少,且为
元,
共有
种方案,当安排
辆大货车和
辆小货车时,总费用最少,为
元.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版2020-2021学年九年级(上)第二章一元二次方程检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;共36分)
1.
一元二次方程
的根为
A.
B.
,
C.
D.
2.
将一元二次方程
化成
(,
为常数)的形式,则
,
的值分别是
A.
,
B.
,
C.
,
D.
,
3.
一个两位数等于它的个位数的平方,且个位数字比十位数字大
,则这个两位数为
A.
B.
C.
或
D.
或
4.
青云超市某服装专柜在销售中发现:进货价为每件
元,销售价为每件
元的某品牌童装平均每天可售出
件.为了迎接"六一",商场决定采取适当的降价措施,扩大销售量,增加盈利.经调查发现:如果每件童装降价
元,那么平均每天就可多售出
件,要想平均每天销售这种童装盈利
元,同时又要使顾客得到较多的实惠,设降价
元,根据题意列方程得
.
A.
B.
C.
D.
5.
已知关于
的一元二次方程
有两个不相等的实数根
,.若
,则
的值是
A.
B.
C.
或
D.
不存在
6.
今年以来,CPI(居民消费价格总水平)的不断上涨已成为热门话题.已知某种食品在9月份的售价为
,11月份的售价为
.求这种食品平均每月上涨的百分率是多少?设这种食品平均每月上涨的百分率为
,根据题意可列方程式为
A.
B.
C.
D.
7.
方程(x-1)(x+3)=12化为ax2+bx+c=0的形式后,a,b,c的值分别为(
)
A.1,2,-15
B.1,-2,-15C.-1,-2,-15
D.-1,2,-15
8.
要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排
场比赛,则参赛球队有
A.
个
B.
个
C.
个
D.
个
9.
关于
的一元二次方程
的一个根是
,则
的值为
A.
B.
C.
或
D.
10.
已知关于
的方程
有两个不相等的实数根,若
,且方程的两个实数根都是整数,则
的值为
A.
B.
或
或
C.
D.
或
或
11.
一个等腰三角形的两边长分别是方程x2-7x+10=0的两根,则该等腰三角形的周长是(
)
A.12
B.9
C.13
D.12或9
12.
对于任意实数
,关于
的方程
的根的情况为
A.
有两个相等的实数根
B.
没有实数根
C.
有两个不相等的实数根
D.
无法判定
二、填空题(共6小题;共24分)
13.
()
?
;
()
?
.
14.
方程
的根是
?.
15.
方程
的根是
?.
16.
某校九年级学生毕业时,每个同学都将自己的相片向全班同学各送一张留作纪念,全班共送了
张相片,如果全班有
名学生,根据题意,列出方程为
?.
17.
如果关于
的一元二次方程
有两个不相等的实根,那么
的取值范围是
?.
18.
已知一个两位数,它的十位数字比个位数字小3,个位数字的平方恰好等于这个两位数,则这个两位数是___________.
三、解答题(共7小题;共60分)
19.
(8分)已知
是方程
的一个根,求
的值.
20.
(6分)
解方程:.
21.
(6分)解方程:.
22.
(8分)
有
个方程:;;;.小静同学解第
个方程
的步骤为:“①
;②
;③
;④
;⑤
;⑥
,.”
(1)小静的解法是从步骤
?
开始出现错误的;
(2)用配方法解第
个方程
.(用含
的式子表示方程的根)
23.
(10分)已知关于
的一元二次方程
.
(1)若方程有实数根,求实数
的取值范围;
(2)若方程两实数根分别为
,,且满足
,实数
的值.
24.
(10分)泰兴鑫都小商品市场以每副60元的价格购进800副羽毛球拍.九月份以单价100元销售,售出了200副.十月份如果销售单价不变,预计仍可售出200副.鑫都小商品市场为增加销售量,决定降价销售.根据市场调查,销售单价每降低5元,可多售出10副,但最低销售单价应高于购进的价格.十月份结束后,批发商将对剩余的羽毛球拍一次性清仓,清仓时销售单价为50元.设十月份销售单价降低x元.
(1)填表:
月份
九月
十月
清仓
销售单价(元)
100
50
销售量(件)
200
(2)如果鑫都小商品市场希望通过销售这批羽毛球拍获利9200元,那么十月份的销售单价应是多少元?
25.
(12分)为加快复工复产,某企业需运输批物资.据调查得知,
辆大货车与
辆小货车一次可以运输
箱;
辆大货车与
辆小货车一次可以运输
箱.
(1)求
辆大货车和
辆小货车一次可以分别运输多少箱物资;
(2)计划用两种货车共
辆运输这批物资,每辆大货车一次需费用
元,每辆小货车一次需费用
元.若运输物资不少于
箱,且总费用小于
元,请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?
答案
第一部分
1.
B
2.
A
3.
A
4.
A
5.
A
6.
B
7.
A
【解析】(1)如图1,,,
在
中,;
(2)如图2,,,
中,.
综上,蚂蚁从点
出发沿纸箱表面爬行到点
的最短距离是
.
8.
C
9.
B
10.
B
【解析】
关于
的方程
有两个不相等的实数根,
,
解得
,
方程的两个实数根都是整数,
是整数,
是完全平方数,
,
或
或
.
11.
若等腰三角形的三边为2,2,5,则2+2<5,不满足三角形三边关系,舍去.故选A.[]
12.
B
【解析】.
不论
为何值,,即
.
方程没有实数根.
第二部分
13.
,,,
14.
,
【解析】,
,
,
,.
15.
,
16.
17.
且
【解析】
关于
的一元二次方程
有两个不相等的实数根,
且
,即
,
解得:
且
.
18.
.25或36
第三部分
19.
是方程
的一个根,
.
即
.
20.
所以
21.
移项,得
即
则
所以
,.
22.
(1)
⑤
??????(2)
移项,得
配方,得
即
解得
即
所以
23.
(1)
根据题意可知,
解得
实数
的取值范围是
.
??????(2)
根据根与系数的关系可知
,.
,
,
即
.
,
解得
.
又
,
不合题意舍去,
.
24.
解:(1)100-x 200+2x 800-200-(200+2x)(3分)
(2)根据题意得100×200+(100-x)(200+2x)+50[800-200-(200+2x)]-60×800=9200,
解得x1=20,x2=-70(舍去).
当x=20时,100-x=80>60,符合题意.
答:十月份的销售单价应是80元.
25.
(1)
设
辆大货车和
辆小货车一次可以分别运输
箱,
箱物资,
根据题意,得:
解得:
答:
辆大货车和
辆小货车一次可以分别运输
箱,
箱物资.
??????(2)
设安排
辆大货车,则小货车
辆,总费用为
,
则
,
解得:,
而
,
解得:,
则
,
则运输方案有
种:
辆大货车和
辆小货车;
辆大货车和
辆小货车;
辆大货车和
辆小货车;
,
当
时,总费用最少,且为
元,
共有
种方案,当安排
辆大货车和
辆小货车时,总费用最少,为
元.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
