4.3.3 余角和补角课件(30张PPT)
文档属性
| 名称 | 4.3.3 余角和补角课件(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-19 22:05:05 | ||
图片预览






文档简介
第四章 几何图形初步
4.3 角
第3课时 余角和补角
2020年秋人教版数学七年级上册精品课件
学习目标
1
2
了解余角、补角的概念,掌握余角和补角的性质,并能利用余角、补角的知识解决相关问题.(重点、难点)
了解方位角的概念,并能用方位角知识解决一些简单的实际问题.(难点)
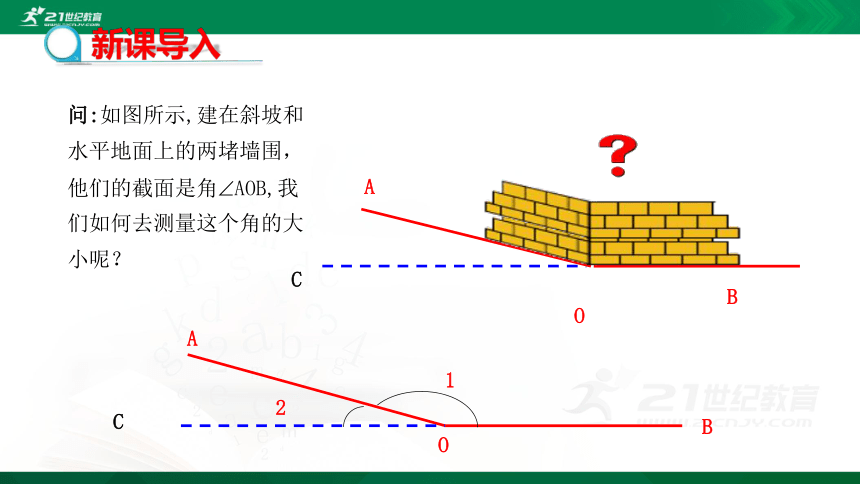
问:如图所示,建在斜坡和水平地面上的两堵墙围,他们的截面是角?AOB,我们如何去测量这个角的大小呢?
C
B
A
O
A
C
O
B
1
2
新课导入
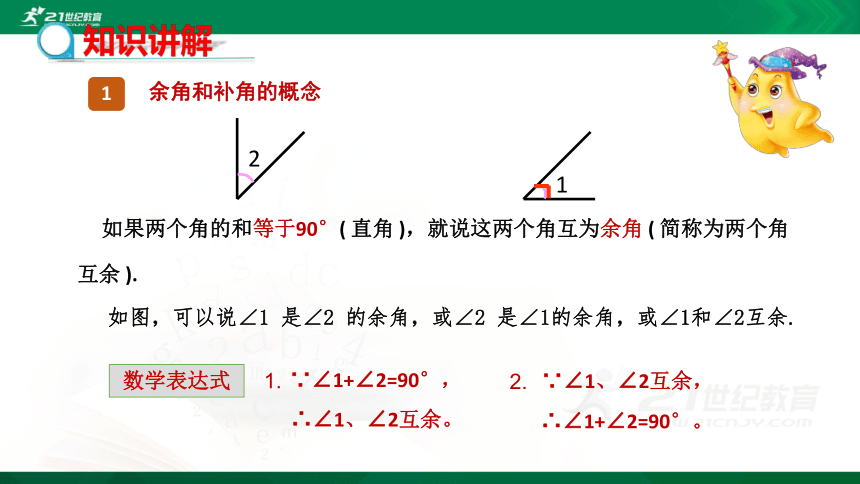
余角和补角的概念
1
如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
如图,可以说∠1 是∠2 的余角,或∠2 是∠1的余角,或∠1和∠2互余.
2
1
知识讲解
∵∠1+∠2=90°,
∴∠1、∠2互余。
∵∠1、∠2互余,
∴∠1+∠2=90°。
1.
2.
数学表达式
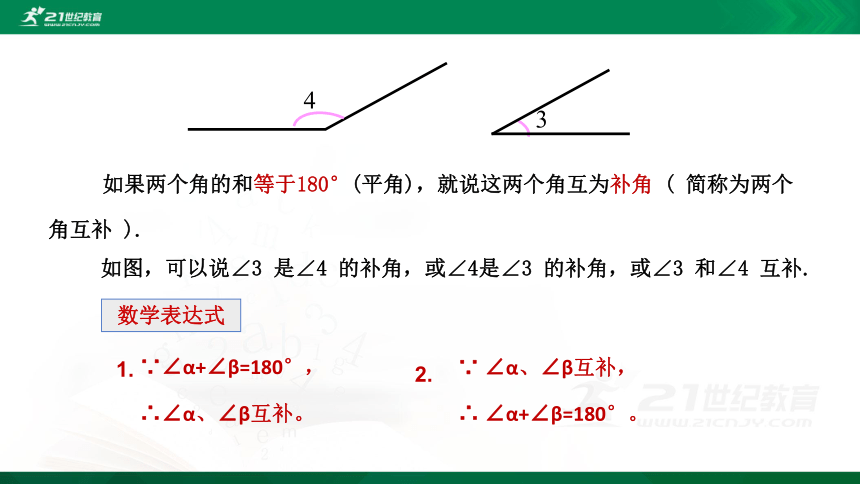
如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
如图,可以说∠3 是∠4 的补角,或∠4是∠3 的补角,或∠3 和∠4 互补.
4
3
数学表达式
∵∠α+∠β=180°,
∴∠α、∠β互补。
1.
2.
∵ ∠α、∠β互补,
∴ ∠α+∠β=180°。
1.判断下列说法是否正确
练一练
(1)90度的角叫余角,180度的角叫补角。 ( )
(3)如果一个角有补角,那么这个角一定是钝角。( )
(4)互补的两个角不可能相等。 ( )
(5)钝角没有余角,但一定有补角。( )
(6)互余的两个角一定都是锐角,两个锐角一定互余.( )
(2)若 ( )
?
?
?
?
?
?
?
(7)互补、互余的两角一定有公共顶点或公共边( )
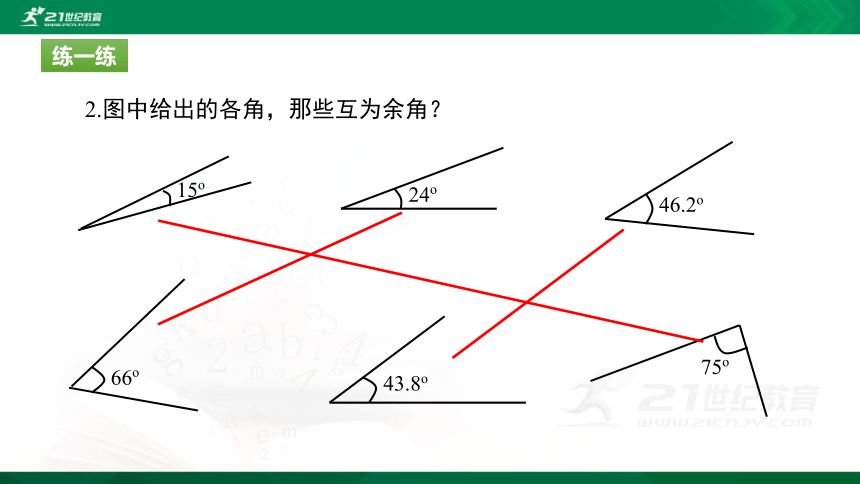
2.图中给出的各角,那些互为余角?
15o
24o
66o
75o
46.2o
43.8o
练一练
3.图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
练一练
例1 若一个角的补角等于它的余角的 4 倍,求这个角的度数.
解:设这个角为 x°,则它的补角是 ( 180-x )°,
余角是 ( 90-x )° .
根据题意,得180-x = 4 ( 90-x ) .
解得 x = 60.
答:这个角的度数是 60 °.
例2 已知 ∠A 与∠B 互余,且 ∠A 的度数比∠B 度数的 3 倍还多30°,求∠B的度数.
解:设∠B的度数为x°,则 ∠A 的度数为 (3x+30)°.
根据题意得: x + ( 3x+30 ) = 90.
解得 x=15.
故 ∠B 的度数为15°.
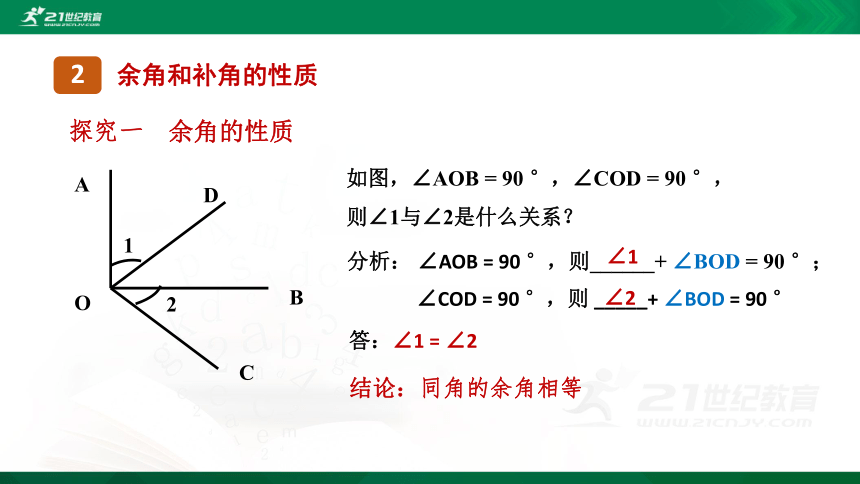
分析: ∠AOB = 90 °,则______+ ∠BOD = 90 °;
结论:同角的余角相等
如图,∠AOB = 90 °,∠COD = 90 °,
则∠1与∠2是什么关系?
A
O
B
C
D
1
2
余角的性质
∠COD = 90 °,则 _____+ ∠BOD = 90 °
答:∠1 = ∠2
∠1
∠2
探究一
2
余角和补角的性质
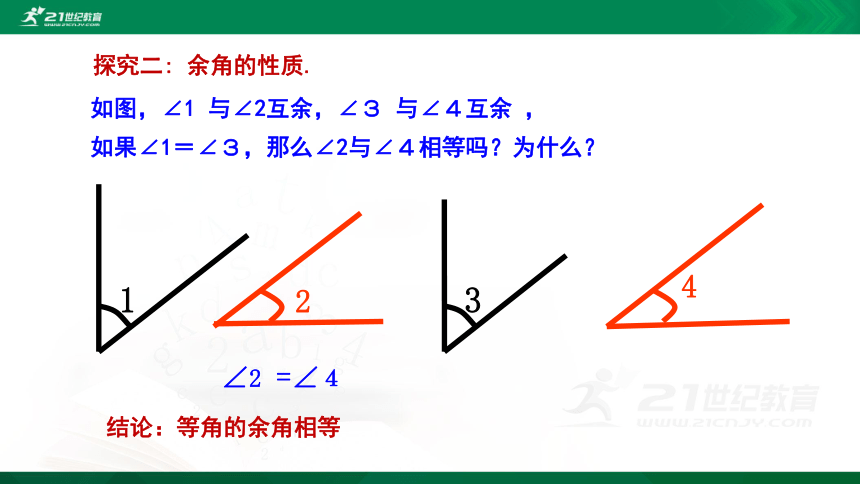
如图,∠1 与∠2互余,∠3 与∠4互余 ,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
结论:等角的余角相等
探究二: 余角的性质.
∠2 =∠4
如图,∠1 与∠2互补,∠1 与∠3互补 ,那么∠2与∠3相等吗?为什么?
补角的性质
∵ ∠1 与∠2互补,
∴ ∠2= 180 °-__;
答:∠2与∠3相等。
结论:同角的补角相等
∵ ∠1与∠3互补 ,
∴_______。
3
1
2
∴ 。
理由如下:
探究三
∠3=180﹣∠1
∠2=∠3
∠1
如图∠1 与∠2互补,∠3 与∠4互补 ,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
探究四:余角和补角的性质.
结论:等角的补角相等.
∠2=∠4
例3 如图,AB是一条直线,OC是一条射线,∠AOC=2∠AOF,∠BOC=2∠BOE.
(1)∠1与∠2互余吗?
解:互余.
∵ ∠AOC=2∠AOF,∠BOC=2∠BOE
∴ ∠AOF= ∠ FOC=???????? ∠AOC, ∠BOE= ∠ COE =???????? ∠AOC
∴ ∠1+ ∠2 =???????? (∠AOC+ ∠BOC) =???????? ×180°=90°,
∴ ∠1与 ∠2 互余.
?
(2)指出图中所有互余和互补的角.
解:互余的角:∠1与∠2;∠1与∠BOE;∠2与∠AOF;∠BOE与∠AOF.
互补的角:∠BOE与∠AOE;∠2与∠AOE;∠AOF与∠BOF;∠1与∠BOF;∠AOC与∠BOC.
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA,
A
B
C
D
OB,
OC,
OD,
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
3
方位角
八大方位
平面图上的方向:
上北,下南,左西,右东
O
北
南
西
东
南偏西25°:
25°
北偏西70°:
南偏东60°:
A
B
C
射线OA
射线OB
射线OC
70°
60°
方位角一般是指以正南或正北的方向为基准,再加上偏东或偏西的角度
东
西
北
南
●
A
如果B在A的
B
●
40°
那么A在B的
北偏东40°,
南偏西40°.
1.一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
A
随堂训练
2.点 C 在点 A 的北偏东60°的方向上,那么点 A在
点 C 的( )方向上.
南偏东30 B. 南偏西30°
C. 南偏东60° D. 南偏西60°
60°
北
60°
30°
A
B
北
北
C
D
3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是_______.
150°
4. ∠1 与 ∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,
则∠1= ,∠2= .
62°
28°
5.如图,∠AOC=90°,∠AOB=∠COD,则∠BOD=____度.
90
6. 如图,将两块直角三角板的直角顶点C叠放在一起.
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30.°,求∠ACB的度数.
解:(1)∠ACE=∠BCD.理由如下:
因为∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,
所以∠ACE=∠BCD.
(2)由余角的定义,得∠ACE=90°-.∠DCE=90°-30°=60°.
由角的和差,得∠ACB=∠ACE+∠BCE=60°+90°=150°.
7.如图①,∠AOC和∠DOB都是直角.
(1)如果∠DOC=32°,求∠AOB的度数;
(2)找出图①中相等的锐角,并说明相等的理由;
(3)在图②中,利用三角板画一个与∠FOE相等的角.
解:(1)因为∠DOC=32°,∠AOC=90°,所以∠AOD=58°.
又因为∠BOD=90°,所以∠AOB=∠AOD+∠BOD=58°+90°=148°.
(2)∠AOD=∠BOC.理由如下:
因为∠AOC=∠BOD,所以∠AOD+∠COD=∠BOC+∠COD.
所以∠AOD=∠BOC.
(3)如图,∠HOG即为所求.
8. 如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东
70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数?
(2)轮船C在∠APB的平分线上,
则轮船C在灯塔P的什么方位?
解:(1)由题意可知∠APN=30°,∠BPS=70°,
所以∠APB=180°-∠APN-∠BPS=80°.
(2)因为PC平分∠APB,且∠APB=80°,所以∠APC=12∠APB=40°.
所以∠NPC=∠APN+∠APC=70°.
所以轮船C在灯塔P的北偏东70°的方向上.
?
互余
互补
图形
数学语言
性质
同角(等角)的余角相等
同角(等角)的补角相等
课堂小结
2.方位角:物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向。
1.余角和补角
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
4.3 角
第3课时 余角和补角
2020年秋人教版数学七年级上册精品课件
学习目标
1
2
了解余角、补角的概念,掌握余角和补角的性质,并能利用余角、补角的知识解决相关问题.(重点、难点)
了解方位角的概念,并能用方位角知识解决一些简单的实际问题.(难点)
问:如图所示,建在斜坡和水平地面上的两堵墙围,他们的截面是角?AOB,我们如何去测量这个角的大小呢?
C
B
A
O
A
C
O
B
1
2
新课导入
余角和补角的概念
1
如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
如图,可以说∠1 是∠2 的余角,或∠2 是∠1的余角,或∠1和∠2互余.
2
1
知识讲解
∵∠1+∠2=90°,
∴∠1、∠2互余。
∵∠1、∠2互余,
∴∠1+∠2=90°。
1.
2.
数学表达式
如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
如图,可以说∠3 是∠4 的补角,或∠4是∠3 的补角,或∠3 和∠4 互补.
4
3
数学表达式
∵∠α+∠β=180°,
∴∠α、∠β互补。
1.
2.
∵ ∠α、∠β互补,
∴ ∠α+∠β=180°。
1.判断下列说法是否正确
练一练
(1)90度的角叫余角,180度的角叫补角。 ( )
(3)如果一个角有补角,那么这个角一定是钝角。( )
(4)互补的两个角不可能相等。 ( )
(5)钝角没有余角,但一定有补角。( )
(6)互余的两个角一定都是锐角,两个锐角一定互余.( )
(2)若 ( )
?
?
?
?
?
?
?
(7)互补、互余的两角一定有公共顶点或公共边( )
2.图中给出的各角,那些互为余角?
15o
24o
66o
75o
46.2o
43.8o
练一练
3.图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
练一练
例1 若一个角的补角等于它的余角的 4 倍,求这个角的度数.
解:设这个角为 x°,则它的补角是 ( 180-x )°,
余角是 ( 90-x )° .
根据题意,得180-x = 4 ( 90-x ) .
解得 x = 60.
答:这个角的度数是 60 °.
例2 已知 ∠A 与∠B 互余,且 ∠A 的度数比∠B 度数的 3 倍还多30°,求∠B的度数.
解:设∠B的度数为x°,则 ∠A 的度数为 (3x+30)°.
根据题意得: x + ( 3x+30 ) = 90.
解得 x=15.
故 ∠B 的度数为15°.
分析: ∠AOB = 90 °,则______+ ∠BOD = 90 °;
结论:同角的余角相等
如图,∠AOB = 90 °,∠COD = 90 °,
则∠1与∠2是什么关系?
A
O
B
C
D
1
2
余角的性质
∠COD = 90 °,则 _____+ ∠BOD = 90 °
答:∠1 = ∠2
∠1
∠2
探究一
2
余角和补角的性质
如图,∠1 与∠2互余,∠3 与∠4互余 ,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
结论:等角的余角相等
探究二: 余角的性质.
∠2 =∠4
如图,∠1 与∠2互补,∠1 与∠3互补 ,那么∠2与∠3相等吗?为什么?
补角的性质
∵ ∠1 与∠2互补,
∴ ∠2= 180 °-__;
答:∠2与∠3相等。
结论:同角的补角相等
∵ ∠1与∠3互补 ,
∴_______。
3
1
2
∴ 。
理由如下:
探究三
∠3=180﹣∠1
∠2=∠3
∠1
如图∠1 与∠2互补,∠3 与∠4互补 ,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
探究四:余角和补角的性质.
结论:等角的补角相等.
∠2=∠4
例3 如图,AB是一条直线,OC是一条射线,∠AOC=2∠AOF,∠BOC=2∠BOE.
(1)∠1与∠2互余吗?
解:互余.
∵ ∠AOC=2∠AOF,∠BOC=2∠BOE
∴ ∠AOF= ∠ FOC=???????? ∠AOC, ∠BOE= ∠ COE =???????? ∠AOC
∴ ∠1+ ∠2 =???????? (∠AOC+ ∠BOC) =???????? ×180°=90°,
∴ ∠1与 ∠2 互余.
?
(2)指出图中所有互余和互补的角.
解:互余的角:∠1与∠2;∠1与∠BOE;∠2与∠AOF;∠BOE与∠AOF.
互补的角:∠BOE与∠AOE;∠2与∠AOE;∠AOF与∠BOF;∠1与∠BOF;∠AOC与∠BOC.
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA,
A
B
C
D
OB,
OC,
OD,
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
3
方位角
八大方位
平面图上的方向:
上北,下南,左西,右东
O
北
南
西
东
南偏西25°:
25°
北偏西70°:
南偏东60°:
A
B
C
射线OA
射线OB
射线OC
70°
60°
方位角一般是指以正南或正北的方向为基准,再加上偏东或偏西的角度
东
西
北
南
●
A
如果B在A的
B
●
40°
那么A在B的
北偏东40°,
南偏西40°.
1.一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
A
随堂训练
2.点 C 在点 A 的北偏东60°的方向上,那么点 A在
点 C 的( )方向上.
南偏东30 B. 南偏西30°
C. 南偏东60° D. 南偏西60°
60°
北
60°
30°
A
B
北
北
C
D
3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是_______.
150°
4. ∠1 与 ∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,
则∠1= ,∠2= .
62°
28°
5.如图,∠AOC=90°,∠AOB=∠COD,则∠BOD=____度.
90
6. 如图,将两块直角三角板的直角顶点C叠放在一起.
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30.°,求∠ACB的度数.
解:(1)∠ACE=∠BCD.理由如下:
因为∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,
所以∠ACE=∠BCD.
(2)由余角的定义,得∠ACE=90°-.∠DCE=90°-30°=60°.
由角的和差,得∠ACB=∠ACE+∠BCE=60°+90°=150°.
7.如图①,∠AOC和∠DOB都是直角.
(1)如果∠DOC=32°,求∠AOB的度数;
(2)找出图①中相等的锐角,并说明相等的理由;
(3)在图②中,利用三角板画一个与∠FOE相等的角.
解:(1)因为∠DOC=32°,∠AOC=90°,所以∠AOD=58°.
又因为∠BOD=90°,所以∠AOB=∠AOD+∠BOD=58°+90°=148°.
(2)∠AOD=∠BOC.理由如下:
因为∠AOC=∠BOD,所以∠AOD+∠COD=∠BOC+∠COD.
所以∠AOD=∠BOC.
(3)如图,∠HOG即为所求.
8. 如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东
70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数?
(2)轮船C在∠APB的平分线上,
则轮船C在灯塔P的什么方位?
解:(1)由题意可知∠APN=30°,∠BPS=70°,
所以∠APB=180°-∠APN-∠BPS=80°.
(2)因为PC平分∠APB,且∠APB=80°,所以∠APC=12∠APB=40°.
所以∠NPC=∠APN+∠APC=70°.
所以轮船C在灯塔P的北偏东70°的方向上.
?
互余
互补
图形
数学语言
性质
同角(等角)的余角相等
同角(等角)的补角相等
课堂小结
2.方位角:物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向。
1.余角和补角
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
