北师大版九年级数学上册同步课时训练:1.1 菱形的性质与判定(含答案)
文档属性
| 名称 | 北师大版九年级数学上册同步课时训练:1.1 菱形的性质与判定(含答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 248.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-19 00:00:00 | ||
图片预览




文档简介
北师大版2020年(秋季)九年级数学上册同步课时训练
1.1 菱形的性质与判定
一.选择题
1.关于菱形,下列说法错误的是( )
A.四条边相等 B.对角线互相垂直
C.四个角相等 D.对角线互相平分
2.如图,丝带重叠的部分一定是( )
A.正方形 B.矩形 C.菱形 D.都有可能
3.如图,添加下列条件仍然不能使?ABCD成为菱形的是( )
A.AB=BC B.AC⊥BD C.∠ABC=90° D.∠1=∠2
4.若菱形的两条对角线长分别为8和6,则这个菱形的面积是( )
A.96 B.48 C.24 D.12
5.如图,菱形ABCD中,∠D=130°,则∠1=( )
A.30° B.25° C.20° D.15°
6.如图,在菱形ABCD中,AE,AF分别垂直平分BC,CD,垂足分别为E,F,则∠EAF的度数是( )
A.90° B.60° C.45° D.30°
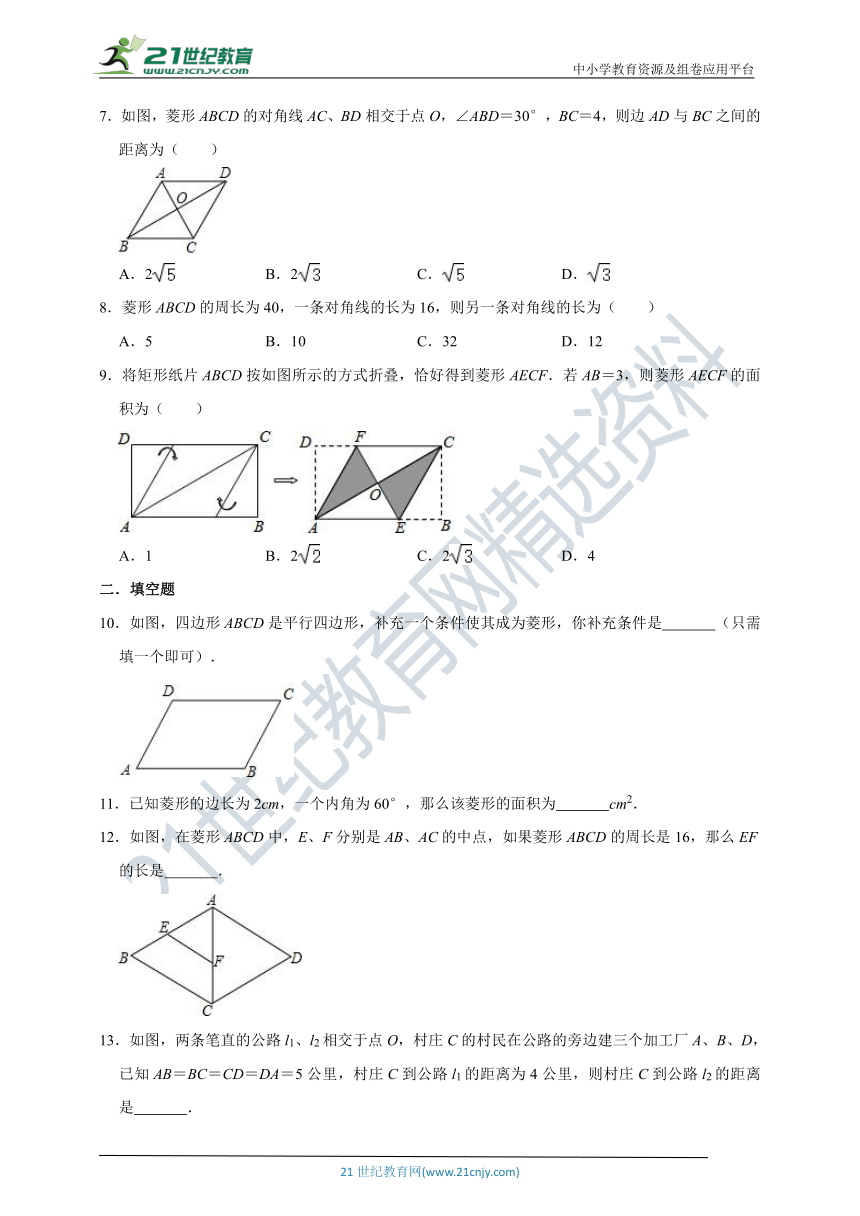
7.如图,菱形ABCD的对角线AC、BD相交于点O,∠ABD=30°,BC=4,则边AD与BC之间的距离为( )
A.2 B.2 C. D.
8.菱形ABCD的周长为40,一条对角线的长为16,则另一条对角线的长为( )
A.5 B.10 C.32 D.12
9.将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
A.1 B.2 C.2 D.4
二.填空题
10.如图,四边形ABCD是平行四边形,补充一个条件使其成为菱形,你补充条件是 (只需填一个即可).
11.已知菱形的边长为2cm,一个内角为60°,那么该菱形的面积为 cm2.
12.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果菱形ABCD的周长是16,那么EF的长是 .
13.如图,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D,已知AB=BC=CD=DA=5公里,村庄C到公路l1的距离为4公里,则村庄C到公路l2的距离是 .
14.如图,菱形ABCD中,AC,BD相交于O,DE⊥BC于E,连接OE,∠BAD=40°,则∠OED的度数为 .
三.解答题
15.如图,AE∥BF,BD平分∠ABC交AE于点D,点C在BF上且BC=AB,连接CD.求证:四边形ABCD是菱形.
16.如图5,四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=2.
(1)求菱形ABCD的周长;
(2)若AC=2,求菱形ABCD的面积.
17.如图,在菱形ABCD中,E为对角线BD上一点,且AE⊥AB,连结CE.
(1)求证:∠ECB=90°;
(2)若AE═ED=1时,求菱形的边长.
18.如图,BD为平行四边形ABCD的对角线,∠ADB=90°,E是AB的中点,F是BD的中点,连接EF并延长交DC于点G,连接BG.
(1)求证:△BEF≌△DGF;
(2)证明四边形DEBG是菱形.
19.如图,在△ABC中,D、E分别是AB、AC的中点,延长DE到点F,使得EF=BE,连接CF.若EC平分∠BEF.
(1)求证:四边形BCFE是菱形;
(2)若AC=8,∠BCF=120°,求菱形BCFE的面积.
20.如图,在菱形ABCD中,∠A=60°,点E、F分别在边AB、BC上,△DEF是等边三角形.
(1)求证:BE=CF;
(2)若DG⊥AB,AD=6,AE=4,求EF的长.
参考答案
一.选择题(共9小题)
1.解:∵菱形的性质有四边相等,对角线互相垂直平分,
∴四个角相等不是菱形的性质,
故选:C.
2.解:过点A作AE⊥BC于E,AF⊥CD于F,因为两条彩带宽度相同,
所以AB∥CD,AD∥BC,AE=AF.
∴四边形ABCD是平行四边形.
∵S?ABCD=BC?AE=CD?AF.又AE=AF.
∴BC=CD,
∴四边形ABCD是菱形.
故选:C.
3.解:A、∵四边形ABCD是平行四边形,AB=BC,
∴平行四边形ABCD是菱形,故本选项错误;
B、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故本选项错误;
C、∵四边形ABCD是平行四边形和∠ABC=90°不能推出,平行四边形ABCD是菱形,故本选项正确;
D、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠2=∠ADB,
∵∠1=∠2,
∴∠1=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形,故本选项错误;
故选:C.
4.解:∵四边形ABCD是菱形,
∴S=×6×8=24.
故选:C.
5.解:∵四边形ABCD是菱形,
∴DC∥AB,∠DAC=∠1,
∵∠D=130°,
∴∠DAB=180°﹣130°=50°,
∴∠1=∠DAB=25°.
故选:B.
6.解:连接AC,
∵AE垂直平分边BC,
∴AB=AC,
又∵四边形ABCD是菱形,
∴AB=BC,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠B=60°,
∴∠BCD=120°,
又∵AF垂直平分边CD,
∴在四边形AECF中,∠EAF=360°﹣180°﹣120°=60°.
故选:B.
7.解:过点A作AE⊥BC,
∵四边形ABCD为菱形,
∴∠ABD=∠CBD,AB=BC,
∵∠ABD=30°,
∴∠ABC=60°,
∴∠BAE=30°,
∴BE=2,AE=2.
即边AD与BC之间的距离为2.
故选:B.
8.解:∵菱形ABCD的周长等于40,
∴边长AB=40÷4=10,
∵AC⊥BD,AO=CO,BO=DO,BD=16,
∴BO=8,
∴OA===6,
∴AC=12,
故选:D.
9.解:∵四边形AECF是菱形,AB=3,
∴假设BE=x,则AE=3﹣x,CE=3﹣x,
∵四边形AECF是菱形,
∴∠FCO=∠ECO,
∵∠ECO=∠ECB,
∴∠ECO=∠ECB=∠FCO=30°,
2BE=CE,
∴CE=2x,
∴2x=3﹣x,
解得:x=1,
∴CE=2,利用勾股定理得出:
BC2+BE2=EC2,
BC===,
又∵AE=AB﹣BE=3﹣1=2,
则菱形的面积是:AE?BC=2.
故选:C.
二.填空题(共5小题)
10.解:∵AB=BC,且四边形ABCD为平行四边形
∴四边形ABCD是菱形
故答案为:AB=BC(答案不唯一)
11.解:连接AC,过点A作AM⊥BC于点M,
∵菱形的边长为2cm,
∴AB=BC=2cm,
∵有一个内角是60°,
∴∠ABC=60°,
∴AM=ABsin60°=,
∴此菱形的面积为:2×=2(cm2).
故答案为:2.
12.解:在菱形ABCD中,周长为16,
∴AB=BC=CD=DA=4,
∵E、F分别是AB、AC的中点,
∴EF=BC=2,
故答案为:2
13.解:连接AC,过点C作CE⊥l2于E,作CF⊥l1于F,
∵村庄C到公路l1的距离为4千米,
∴CF=4千米,
∵AB=BC=CD=DA,
∴四边形ABCD是菱形,
∴AC平分∠BAD,
∴CE=CF=4千米,
即C到公路l2的距离是4千米.
故答案是:4千米.
14.解:∵四边形ABCD是菱形,∠BAD=40°,
∴∠DAO=BAD=20°,AC⊥BD,DO=BO,AD∥BC,
∴∠DOA=90°,
∴∠ADO=90°﹣∠DAO=70°,
∵AD∥BC,DE⊥BC,
∴DE⊥AD,
∴∠ADE=90°,
∴∠ODE=∠AD∠E﹣∠ADO=20°,
∵DE⊥BC,
∴∠DEB=90°,
∵DO=BO,
∴OE=BD=OD,
∴∠OED=∠ODE=20°,
故答案为:20°.
三.解答题(共6小题)
15.证明:∵AE∥BF,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠DBC=∠ABD,
∴∠ADB=∠ABD,
∴AB=AD,
又∵AB=BC,
∴AD=BC,
∵AE∥BF,即AD∥BC,
∴四边形ABCD为平行四边形,
又∵AB=AD,
∴四边形ABCD为菱形.
16.解:(1)∵四边形ABCD是菱形,AB=2,
∴BC=CD=AD=AB=2,
∴菱形ABCD的周长=4AB=8;
(2)∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=1,
∴OB===,
∴BD=2OB=2,
∴形ABCD的面积=AC×BD=×2×2=2.
17.证明:(1)∵AE⊥BC,
∴∠BAE=90°,
∵四边形ABCD是菱形,
∴AB=BC,∠ABD=∠CBD,
又∵BE=BE,
∴△ABE≌△CBE(SAS),
∴∠BAE=∠BCE=90°;
(2)如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,BH=DH,AH=CH,
∴∠ABD=∠ADB,
∵AE═ED=1,
∴∠DAE=∠EDA,
∴∠DAE=∠ADE=∠ABD,
∵∠DAE+∠ADE+∠BAE+∠ABD=180°,
∴∠DAE=∠ADE=∠ABD=30°,
∴BE=2AE=2,
∴BD=BE+DE=3,
∴BH=DH=,
∵∠ABD=30°,AH⊥BD,
∴AB=2AH,BH=AH,
∴AH=,AB=2AH=,
∴菱形的边长为.
18.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠FEB=∠FGD,∠FBE=∠FDG,
∵F是BD的中点,
∴BF=DF,
在△BEF和△DGF中,,
∴△BEF≌△DGF(AAS);
(2)由(1)得:△BEF≌△DGF,
∴BE=DG,
∵BE∥DG,
∴四边形DEBG是平行四边形,
∵∠ADB=90°,E是AB的中点,
∴DE=AB=BE,
∴四边形DEBG是菱形.
19.(1)证明:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
∴∠FEC=∠BCE.
∵EC平分∠BEF,
∴∠BEC=∠FEC,
∴∠BEC=∠BCE,
∴BE=BC,
又∵EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=EF,
∴四边形BCFE是菱形;
(2)解:∵AC=8,D是AC的中点,
∴EC=AC=8=4.
∵∠BCF=120°,
∴∠ECB=∠BCF=120°=60°,
又∵在菱形BCEF中,BE=BC,
∴△EBC是等边三角形,
∴BE=BC=CE,
过点E作EG⊥BC于点G,如图:
∴BG=BC=4=2,
∴EG==,
∴S菱形BCFE=BC?EG=4×=.
20.解:(1)证明:∵四边形ABCD是菱形,
∴AB=AD=BC=DC,∠C=∠A=60°,
∴△ABD和△BCD是等边三角形,
∴∠BDC=60°,DC=DB,
∵△DEF是等边三角形,
∴∠EDF=60°,DF=DE,
∴∠CDF=∠BDE,
∴△CDF≌△BDE(SAS),
∴BE=CF;
(2)∴△ABD是等边三角形,DG⊥AB,
∴AG=BG=AB=AD=3,
∴DG=AG=3,
∴EG=AE﹣AG=1,
在Rt△DGE中,根据勾股定理,得
DE==2,
∴EF=DE=2.
1.1 菱形的性质与判定
一.选择题
1.关于菱形,下列说法错误的是( )
A.四条边相等 B.对角线互相垂直
C.四个角相等 D.对角线互相平分
2.如图,丝带重叠的部分一定是( )
A.正方形 B.矩形 C.菱形 D.都有可能
3.如图,添加下列条件仍然不能使?ABCD成为菱形的是( )
A.AB=BC B.AC⊥BD C.∠ABC=90° D.∠1=∠2
4.若菱形的两条对角线长分别为8和6,则这个菱形的面积是( )
A.96 B.48 C.24 D.12
5.如图,菱形ABCD中,∠D=130°,则∠1=( )
A.30° B.25° C.20° D.15°
6.如图,在菱形ABCD中,AE,AF分别垂直平分BC,CD,垂足分别为E,F,则∠EAF的度数是( )
A.90° B.60° C.45° D.30°
7.如图,菱形ABCD的对角线AC、BD相交于点O,∠ABD=30°,BC=4,则边AD与BC之间的距离为( )
A.2 B.2 C. D.
8.菱形ABCD的周长为40,一条对角线的长为16,则另一条对角线的长为( )
A.5 B.10 C.32 D.12
9.将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
A.1 B.2 C.2 D.4
二.填空题
10.如图,四边形ABCD是平行四边形,补充一个条件使其成为菱形,你补充条件是 (只需填一个即可).
11.已知菱形的边长为2cm,一个内角为60°,那么该菱形的面积为 cm2.
12.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果菱形ABCD的周长是16,那么EF的长是 .
13.如图,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D,已知AB=BC=CD=DA=5公里,村庄C到公路l1的距离为4公里,则村庄C到公路l2的距离是 .
14.如图,菱形ABCD中,AC,BD相交于O,DE⊥BC于E,连接OE,∠BAD=40°,则∠OED的度数为 .
三.解答题
15.如图,AE∥BF,BD平分∠ABC交AE于点D,点C在BF上且BC=AB,连接CD.求证:四边形ABCD是菱形.
16.如图5,四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=2.
(1)求菱形ABCD的周长;
(2)若AC=2,求菱形ABCD的面积.
17.如图,在菱形ABCD中,E为对角线BD上一点,且AE⊥AB,连结CE.
(1)求证:∠ECB=90°;
(2)若AE═ED=1时,求菱形的边长.
18.如图,BD为平行四边形ABCD的对角线,∠ADB=90°,E是AB的中点,F是BD的中点,连接EF并延长交DC于点G,连接BG.
(1)求证:△BEF≌△DGF;
(2)证明四边形DEBG是菱形.
19.如图,在△ABC中,D、E分别是AB、AC的中点,延长DE到点F,使得EF=BE,连接CF.若EC平分∠BEF.
(1)求证:四边形BCFE是菱形;
(2)若AC=8,∠BCF=120°,求菱形BCFE的面积.
20.如图,在菱形ABCD中,∠A=60°,点E、F分别在边AB、BC上,△DEF是等边三角形.
(1)求证:BE=CF;
(2)若DG⊥AB,AD=6,AE=4,求EF的长.
参考答案
一.选择题(共9小题)
1.解:∵菱形的性质有四边相等,对角线互相垂直平分,
∴四个角相等不是菱形的性质,
故选:C.
2.解:过点A作AE⊥BC于E,AF⊥CD于F,因为两条彩带宽度相同,
所以AB∥CD,AD∥BC,AE=AF.
∴四边形ABCD是平行四边形.
∵S?ABCD=BC?AE=CD?AF.又AE=AF.
∴BC=CD,
∴四边形ABCD是菱形.
故选:C.
3.解:A、∵四边形ABCD是平行四边形,AB=BC,
∴平行四边形ABCD是菱形,故本选项错误;
B、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故本选项错误;
C、∵四边形ABCD是平行四边形和∠ABC=90°不能推出,平行四边形ABCD是菱形,故本选项正确;
D、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠2=∠ADB,
∵∠1=∠2,
∴∠1=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形,故本选项错误;
故选:C.
4.解:∵四边形ABCD是菱形,
∴S=×6×8=24.
故选:C.
5.解:∵四边形ABCD是菱形,
∴DC∥AB,∠DAC=∠1,
∵∠D=130°,
∴∠DAB=180°﹣130°=50°,
∴∠1=∠DAB=25°.
故选:B.
6.解:连接AC,
∵AE垂直平分边BC,
∴AB=AC,
又∵四边形ABCD是菱形,
∴AB=BC,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠B=60°,
∴∠BCD=120°,
又∵AF垂直平分边CD,
∴在四边形AECF中,∠EAF=360°﹣180°﹣120°=60°.
故选:B.
7.解:过点A作AE⊥BC,
∵四边形ABCD为菱形,
∴∠ABD=∠CBD,AB=BC,
∵∠ABD=30°,
∴∠ABC=60°,
∴∠BAE=30°,
∴BE=2,AE=2.
即边AD与BC之间的距离为2.
故选:B.
8.解:∵菱形ABCD的周长等于40,
∴边长AB=40÷4=10,
∵AC⊥BD,AO=CO,BO=DO,BD=16,
∴BO=8,
∴OA===6,
∴AC=12,
故选:D.
9.解:∵四边形AECF是菱形,AB=3,
∴假设BE=x,则AE=3﹣x,CE=3﹣x,
∵四边形AECF是菱形,
∴∠FCO=∠ECO,
∵∠ECO=∠ECB,
∴∠ECO=∠ECB=∠FCO=30°,
2BE=CE,
∴CE=2x,
∴2x=3﹣x,
解得:x=1,
∴CE=2,利用勾股定理得出:
BC2+BE2=EC2,
BC===,
又∵AE=AB﹣BE=3﹣1=2,
则菱形的面积是:AE?BC=2.
故选:C.
二.填空题(共5小题)
10.解:∵AB=BC,且四边形ABCD为平行四边形
∴四边形ABCD是菱形
故答案为:AB=BC(答案不唯一)
11.解:连接AC,过点A作AM⊥BC于点M,
∵菱形的边长为2cm,
∴AB=BC=2cm,
∵有一个内角是60°,
∴∠ABC=60°,
∴AM=ABsin60°=,
∴此菱形的面积为:2×=2(cm2).
故答案为:2.
12.解:在菱形ABCD中,周长为16,
∴AB=BC=CD=DA=4,
∵E、F分别是AB、AC的中点,
∴EF=BC=2,
故答案为:2
13.解:连接AC,过点C作CE⊥l2于E,作CF⊥l1于F,
∵村庄C到公路l1的距离为4千米,
∴CF=4千米,
∵AB=BC=CD=DA,
∴四边形ABCD是菱形,
∴AC平分∠BAD,
∴CE=CF=4千米,
即C到公路l2的距离是4千米.
故答案是:4千米.
14.解:∵四边形ABCD是菱形,∠BAD=40°,
∴∠DAO=BAD=20°,AC⊥BD,DO=BO,AD∥BC,
∴∠DOA=90°,
∴∠ADO=90°﹣∠DAO=70°,
∵AD∥BC,DE⊥BC,
∴DE⊥AD,
∴∠ADE=90°,
∴∠ODE=∠AD∠E﹣∠ADO=20°,
∵DE⊥BC,
∴∠DEB=90°,
∵DO=BO,
∴OE=BD=OD,
∴∠OED=∠ODE=20°,
故答案为:20°.
三.解答题(共6小题)
15.证明:∵AE∥BF,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠DBC=∠ABD,
∴∠ADB=∠ABD,
∴AB=AD,
又∵AB=BC,
∴AD=BC,
∵AE∥BF,即AD∥BC,
∴四边形ABCD为平行四边形,
又∵AB=AD,
∴四边形ABCD为菱形.
16.解:(1)∵四边形ABCD是菱形,AB=2,
∴BC=CD=AD=AB=2,
∴菱形ABCD的周长=4AB=8;
(2)∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=1,
∴OB===,
∴BD=2OB=2,
∴形ABCD的面积=AC×BD=×2×2=2.
17.证明:(1)∵AE⊥BC,
∴∠BAE=90°,
∵四边形ABCD是菱形,
∴AB=BC,∠ABD=∠CBD,
又∵BE=BE,
∴△ABE≌△CBE(SAS),
∴∠BAE=∠BCE=90°;
(2)如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,BH=DH,AH=CH,
∴∠ABD=∠ADB,
∵AE═ED=1,
∴∠DAE=∠EDA,
∴∠DAE=∠ADE=∠ABD,
∵∠DAE+∠ADE+∠BAE+∠ABD=180°,
∴∠DAE=∠ADE=∠ABD=30°,
∴BE=2AE=2,
∴BD=BE+DE=3,
∴BH=DH=,
∵∠ABD=30°,AH⊥BD,
∴AB=2AH,BH=AH,
∴AH=,AB=2AH=,
∴菱形的边长为.
18.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠FEB=∠FGD,∠FBE=∠FDG,
∵F是BD的中点,
∴BF=DF,
在△BEF和△DGF中,,
∴△BEF≌△DGF(AAS);
(2)由(1)得:△BEF≌△DGF,
∴BE=DG,
∵BE∥DG,
∴四边形DEBG是平行四边形,
∵∠ADB=90°,E是AB的中点,
∴DE=AB=BE,
∴四边形DEBG是菱形.
19.(1)证明:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
∴∠FEC=∠BCE.
∵EC平分∠BEF,
∴∠BEC=∠FEC,
∴∠BEC=∠BCE,
∴BE=BC,
又∵EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=EF,
∴四边形BCFE是菱形;
(2)解:∵AC=8,D是AC的中点,
∴EC=AC=8=4.
∵∠BCF=120°,
∴∠ECB=∠BCF=120°=60°,
又∵在菱形BCEF中,BE=BC,
∴△EBC是等边三角形,
∴BE=BC=CE,
过点E作EG⊥BC于点G,如图:
∴BG=BC=4=2,
∴EG==,
∴S菱形BCFE=BC?EG=4×=.
20.解:(1)证明:∵四边形ABCD是菱形,
∴AB=AD=BC=DC,∠C=∠A=60°,
∴△ABD和△BCD是等边三角形,
∴∠BDC=60°,DC=DB,
∵△DEF是等边三角形,
∴∠EDF=60°,DF=DE,
∴∠CDF=∠BDE,
∴△CDF≌△BDE(SAS),
∴BE=CF;
(2)∴△ABD是等边三角形,DG⊥AB,
∴AG=BG=AB=AD=3,
∴DG=AG=3,
∴EG=AE﹣AG=1,
在Rt△DGE中,根据勾股定理,得
DE==2,
∴EF=DE=2.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
