人教版(五四制)七上:12.1 相交线 (同位角、内错角、同旁内角) 课件 (共14张ppt)
文档属性
| 名称 | 人教版(五四制)七上:12.1 相交线 (同位角、内错角、同旁内角) 课件 (共14张ppt) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-19 19:19:10 | ||
图片预览


文档简介
12.1.3 同位角、内错角、同旁内角
知识回顾:指出右图中所有的邻补角和对顶角?
三条直线相交可分为几种情况?
活动1
探究一:情境导入
结论:
①三条直线相交于一点;
②两条直线被第三条直线所截.
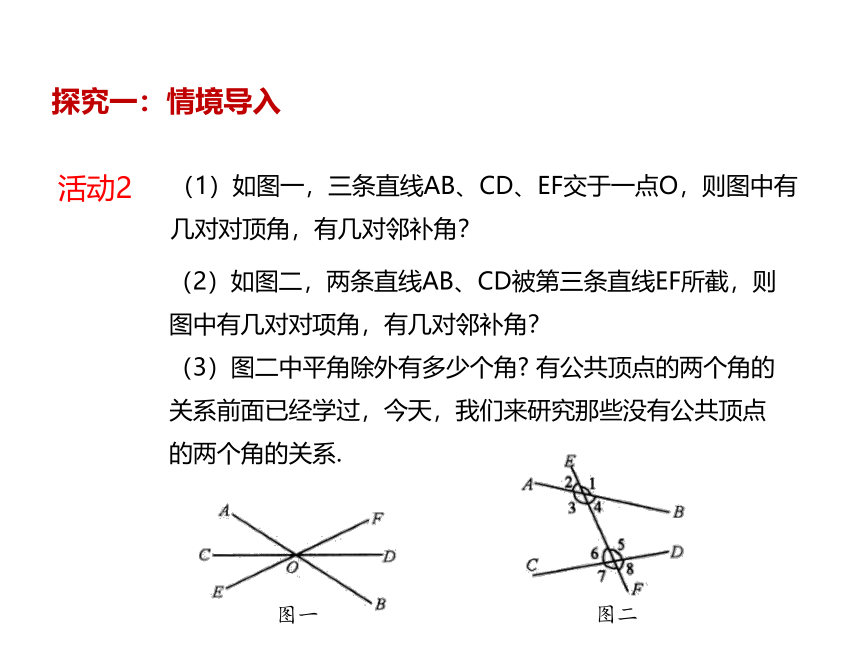
(1)如图一,三条直线AB、CD、EF交于一点O,则图中有几对对顶角,有几对邻补角?
活动2
探究一:情境导入
(2)如图二,两条直线AB、CD被第三条直线EF所截,则图中有几对对项角,有几对邻补角?
图一
图二
(3)图二中平角除外有多少个角? 有公共顶点的两个角的关系前面已经学过,今天,我们来研究那些没有公共顶点的两个角的关系.
同位角
活动1
探究二:识别同位角
(1)如图,∠1和∠5,分别在直线AB、CD的 ,在直线EF的 .具有这种位置关系关系的一对角叫做同位角.
具有这种位置关系关系的一对角叫做同位角.
(2)找出图中还有哪几对角构成同位角?
同位角特征:两直线同旁,截线同侧,形如字母F或倒置
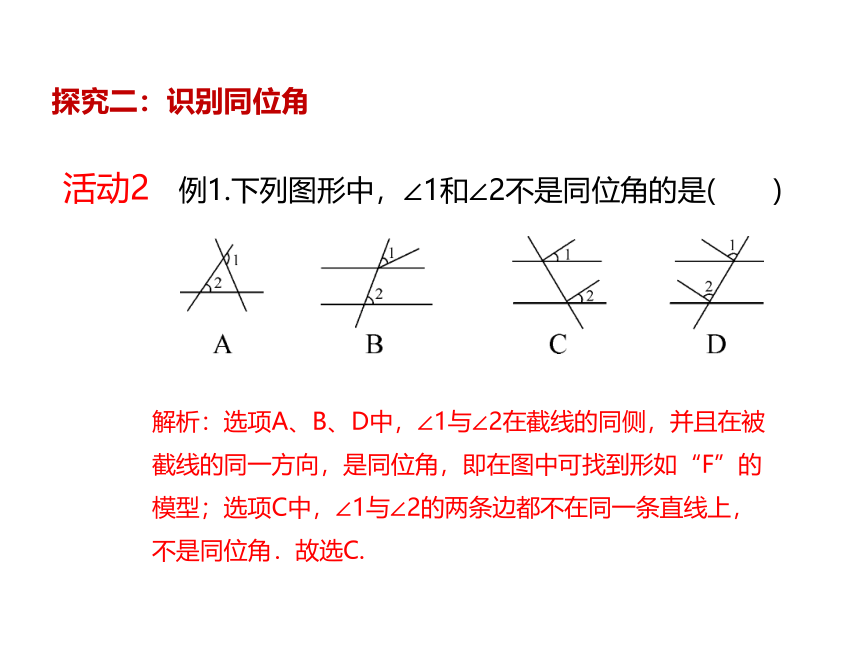
例1.下列图形中,∠1和∠2不是同位角的是( )
活动2
探究二:识别同位角
解析:选项A、B、D中,∠1与∠2在截线的同侧,并且在被截线的同一方向,是同位角,即在图中可找到形如“F”的模型;选项C中,∠1与∠2的两条边都不在同一条直线上,不是同位角.故选C.
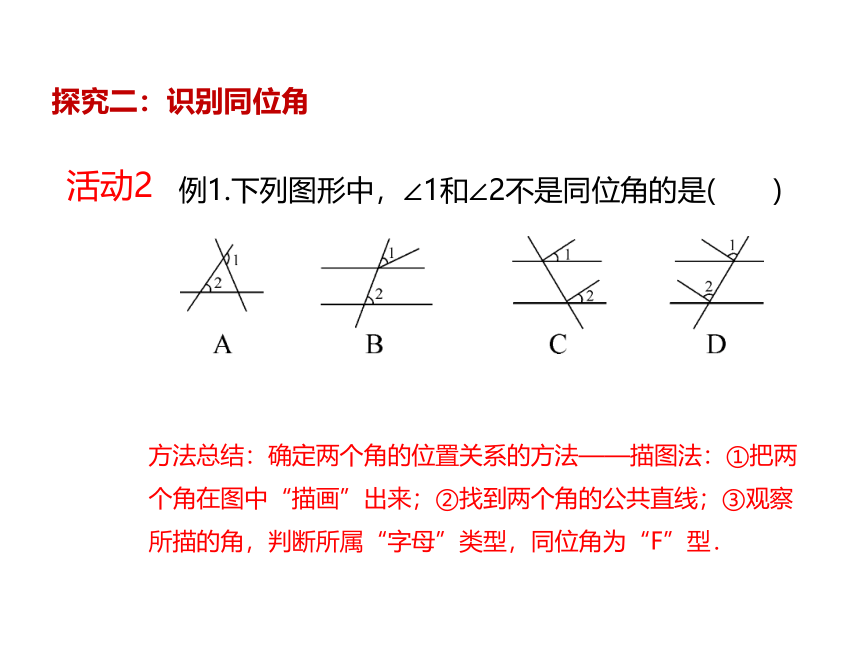
例1.下列图形中,∠1和∠2不是同位角的是( )
探究二:识别同位角
方法总结:确定两个角的位置关系的方法——描图法:①把两个角在图中“描画”出来;②找到两个角的公共直线;③观察所描的角,判断所属“字母”类型,同位角为“F”型.
活动2
(1)如图,∠3和∠5,分别在直线AB、CD的 ,在直线EF的 .具有这种位置关系关系的一对角叫做内错角.
活动1
探究二:识别内错角、同旁内角
内错角特征:两直线间,截线两侧,形如字母Z或反置
内错角
(2)请你找出图中还有哪几对角构成内错角.
(1)如图,∠3和∠6,分别在直线AB、CD的 ,在直线EF的 .具有这种位置关系关系的一对角叫做同旁内角.
活动2
探究二:识别内错角、同旁内角
同旁内角特征:两直线间,截线同侧,形如字母U
同旁内角
(2)请你找出图中还有哪几对角构成同旁内角.
例2、如图,下列说法错误的是( )
活动3
探究三:同位角、内错角、同旁内角
初步应用
A.∠4与∠6是同旁内角 B.∠3与∠1是同旁内角
C.∠2与∠4是内错角 D.∠5与∠4是内错角
解析:根据同位角、内错角、同旁内角的基本模型判断.
A中∠4与∠6形成“U”型,是同旁内角;
B中∠3与∠1形成“U”型,是同旁内角;
C中∠2与∠4不是两直线被一直线所截形成的,不是内错角;
D中∠5与∠4是形成“Z”型,是内错角.故选C.
例2、如图,下列说法错误的是( )
活动3
初步应用
A.∠4与∠6是同旁内角 B.∠3与∠1是同旁内角
C.∠2与∠4是内错角 D.∠5与∠4是内错角
方法总结:在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F”型,内错角的边构成“Z”型,同旁内角的边构成“U”
探究三:同位角、内错角、同旁内角
如图所示,直线DE与∠O的两边相交,则∠O的同位角是________,∠8的同旁内角是________∠8的内错角是________.
活动4
变式练习
解析:直线DE与∠O的两边相交,则∠O的同位角是∠5和∠2,∠8的同旁内角是∠1和∠O.故答案为∠5和∠2,∠1和∠O. ∠2
方法总结:找某角的同位角、内错角、同旁内角时,应从各个方位观察,避免漏数.
探究三:同位角、内错角、同旁内角
(1)这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角;
课堂小结:
(2)同位角、内错角、同旁内角的特点:
角的名称
同位角
内错角
同旁内角
位置特征
基本图形
图形结构特征
两直线的同侧
截线的同旁
两直线的之间
截线的异侧
两直线的之间
截线的同侧
形如字母“F”
或“F”倒置
形如字母“Z”
或“Z”反置
形如字母“U”
确定两个角的位置关系的有效方法——描图法:
①把两个角在图中“描画”出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型。
课堂小结:
知识回顾:指出右图中所有的邻补角和对顶角?
三条直线相交可分为几种情况?
活动1
探究一:情境导入
结论:
①三条直线相交于一点;
②两条直线被第三条直线所截.
(1)如图一,三条直线AB、CD、EF交于一点O,则图中有几对对顶角,有几对邻补角?
活动2
探究一:情境导入
(2)如图二,两条直线AB、CD被第三条直线EF所截,则图中有几对对项角,有几对邻补角?
图一
图二
(3)图二中平角除外有多少个角? 有公共顶点的两个角的关系前面已经学过,今天,我们来研究那些没有公共顶点的两个角的关系.
同位角
活动1
探究二:识别同位角
(1)如图,∠1和∠5,分别在直线AB、CD的 ,在直线EF的 .具有这种位置关系关系的一对角叫做同位角.
具有这种位置关系关系的一对角叫做同位角.
(2)找出图中还有哪几对角构成同位角?
同位角特征:两直线同旁,截线同侧,形如字母F或倒置
例1.下列图形中,∠1和∠2不是同位角的是( )
活动2
探究二:识别同位角
解析:选项A、B、D中,∠1与∠2在截线的同侧,并且在被截线的同一方向,是同位角,即在图中可找到形如“F”的模型;选项C中,∠1与∠2的两条边都不在同一条直线上,不是同位角.故选C.
例1.下列图形中,∠1和∠2不是同位角的是( )
探究二:识别同位角
方法总结:确定两个角的位置关系的方法——描图法:①把两个角在图中“描画”出来;②找到两个角的公共直线;③观察所描的角,判断所属“字母”类型,同位角为“F”型.
活动2
(1)如图,∠3和∠5,分别在直线AB、CD的 ,在直线EF的 .具有这种位置关系关系的一对角叫做内错角.
活动1
探究二:识别内错角、同旁内角
内错角特征:两直线间,截线两侧,形如字母Z或反置
内错角
(2)请你找出图中还有哪几对角构成内错角.
(1)如图,∠3和∠6,分别在直线AB、CD的 ,在直线EF的 .具有这种位置关系关系的一对角叫做同旁内角.
活动2
探究二:识别内错角、同旁内角
同旁内角特征:两直线间,截线同侧,形如字母U
同旁内角
(2)请你找出图中还有哪几对角构成同旁内角.
例2、如图,下列说法错误的是( )
活动3
探究三:同位角、内错角、同旁内角
初步应用
A.∠4与∠6是同旁内角 B.∠3与∠1是同旁内角
C.∠2与∠4是内错角 D.∠5与∠4是内错角
解析:根据同位角、内错角、同旁内角的基本模型判断.
A中∠4与∠6形成“U”型,是同旁内角;
B中∠3与∠1形成“U”型,是同旁内角;
C中∠2与∠4不是两直线被一直线所截形成的,不是内错角;
D中∠5与∠4是形成“Z”型,是内错角.故选C.
例2、如图,下列说法错误的是( )
活动3
初步应用
A.∠4与∠6是同旁内角 B.∠3与∠1是同旁内角
C.∠2与∠4是内错角 D.∠5与∠4是内错角
方法总结:在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F”型,内错角的边构成“Z”型,同旁内角的边构成“U”
探究三:同位角、内错角、同旁内角
如图所示,直线DE与∠O的两边相交,则∠O的同位角是________,∠8的同旁内角是________∠8的内错角是________.
活动4
变式练习
解析:直线DE与∠O的两边相交,则∠O的同位角是∠5和∠2,∠8的同旁内角是∠1和∠O.故答案为∠5和∠2,∠1和∠O. ∠2
方法总结:找某角的同位角、内错角、同旁内角时,应从各个方位观察,避免漏数.
探究三:同位角、内错角、同旁内角
(1)这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角;
课堂小结:
(2)同位角、内错角、同旁内角的特点:
角的名称
同位角
内错角
同旁内角
位置特征
基本图形
图形结构特征
两直线的同侧
截线的同旁
两直线的之间
截线的异侧
两直线的之间
截线的同侧
形如字母“F”
或“F”倒置
形如字母“Z”
或“Z”反置
形如字母“U”
确定两个角的位置关系的有效方法——描图法:
①把两个角在图中“描画”出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型。
课堂小结:
