人教版(五四制)数学六上 6.1 比例的意义和基本性质 (比例的基本性质) 课件 (共36张ppt)
文档属性
| 名称 | 人教版(五四制)数学六上 6.1 比例的意义和基本性质 (比例的基本性质) 课件 (共36张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-19 19:20:30 | ||
图片预览









文档简介
比例的基本性质
复习
1、什么叫做比?
两个数相除又叫做两个数的比。
2、什么叫做比值?
比的前项除以比的后项所得的商,叫做比值。
3、什么叫做比的基本性质?
比的前项和后项同时乘或者除以相同
的数(0 除外),比值不变。
口算下面各比的值,哪些比的比值相等?
12 : 16
5 : 3
10 : 6
9 : 15
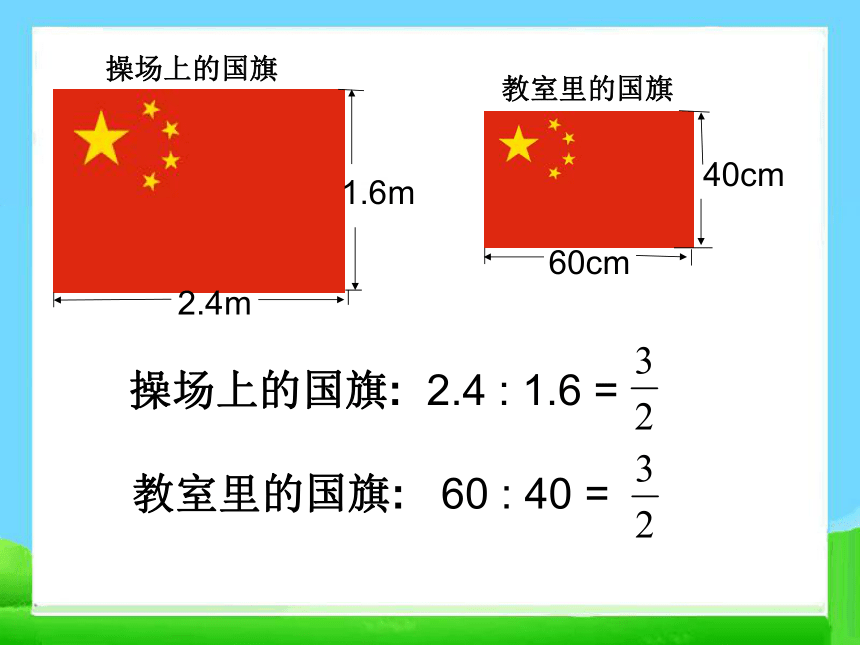
操场上的国旗: 2.4 : 1.6 =
教室里的国旗: 60 : 40 =
2.4m
1.6m
操场上的国旗
40cm
60cm
教室里的国旗
2.4︰1.6
求出它们的比值,你发现了什么?
60︰40
=
=
或
表示两个比相等的式子叫做比例。
比例有两种表达的形式可以用比号连接也可以用分数线连接
判断两个比能不能组成比例,要看它们的比值是否相等。
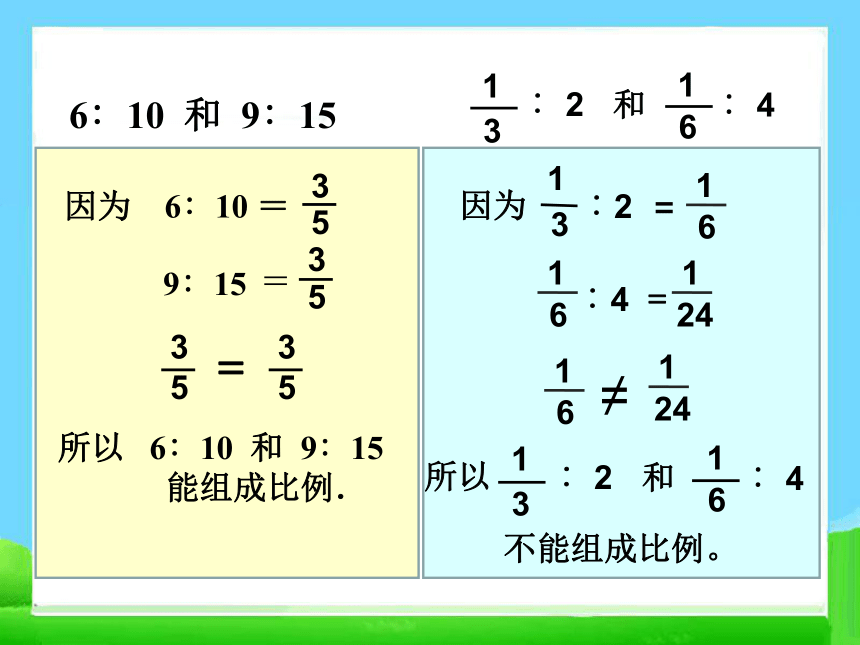
判断下面的两个比能不能组成比例.
6∶10 和 9∶15
3
1
︰
2
1
6
︰
4
和
6∶10 和 9∶15
所以 6∶10 和 9∶15
能组成比例.
因为 6∶10 =
3
5
9∶15 =
3
5
=
3
5
3
5
3
1
︰
2
1
6
︰
4
和
3
1
︰2 =
因为
1
6
︰4 =
1
6
1
24
1
6
≠
1
24
所以
不能组成比例。
3
1
︰
2
1
6
︰
4
和
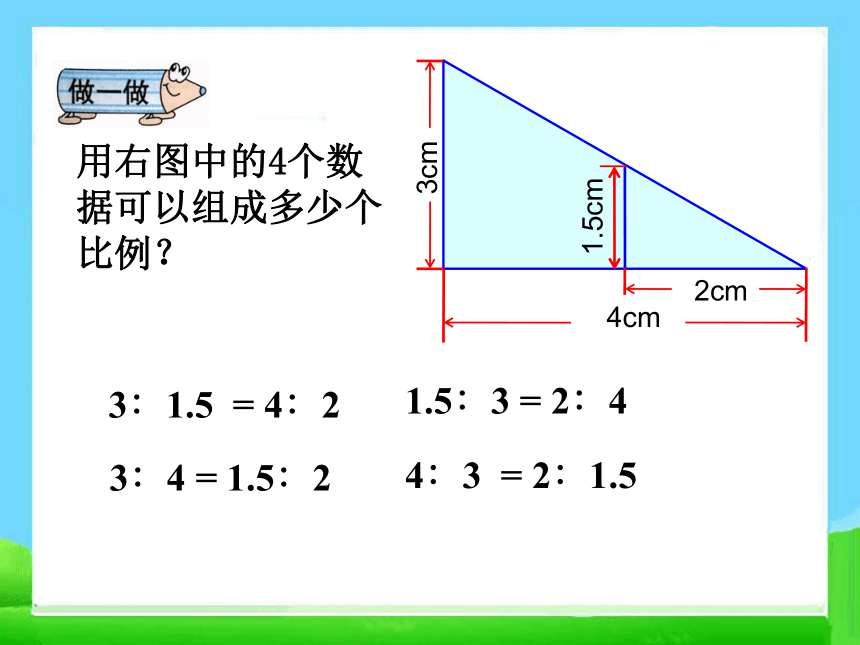
做一做
填空
如果两个比的比值相等,那么这两个比就( )比例.
一个比例,等号左边的比和等号右边的比一定是( )的.
能组成
相等
2cm
4cm
1.5cm
3cm
用右图中的4个数据可以组成多少个比例?
3∶1.5 = 4∶2
3∶4 = 1.5∶2
1.5∶3 = 2∶4
4∶3 = 2∶1.5
2.4 ︰1.6
60 ︰ 40
=
内项
外项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
指出下面比例的外项和内项.
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
做一做
∶
=
6 ∶4
外项
外项
内项
内项
外项
内项
2.4 ︰ 1.6
60 ︰40
=
外项
内项
内项积是:
1.6 × 60=96
外项积是:
2.4 × 40 = 96
2.4
40
1.6
60
×
×
=
计算下面比例的外项积和内项积.
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
做一做
∶
=
6 ∶4
0.6 ∶0.2
∶
=
4.5 × 6 = 27
外项积:
内项积:
外项积:
内项积:
外项积:
内项积:
外项积:
内项积:
2.7 × 10 = 27
6 × 15 = 90
10 × 9 = 90
× 4 = 2
× 6 = 2
0.6 ×
= 0.15
0.2 ×
= 0.15
2.4︰1.6 = 60︰40
在比例里,两个外项的积等于两个内项的积。
交叉相乘
2.4×40=1.6×60
2.4
1.6
=
60
40
比例的基本性质
应用比例的基本性质,判断下面两个比能不能组成比例。
0.2∶2.5 和 4∶50
因为 0.2 × 50 = 10
2.5 × 4 = 10
所以 0.2∶2.5 和4∶50 能组成比例。
10 = 10
1.2∶ 和 ∶5
因为 1.2 × 5 = 6
× =
6≠
所以 1.2∶ 和 ∶5
不能组成比例。
0.5×2 =( )×( )
0.5
5
=
0.2
2
2
5
︰
1
2
=
3
5
︰
3
4
× =( )×( )
2
5
3
4
8︰25=40︰125
( )×( ) =( )×( )
试一试
5
0.2
1
2
3
5
8
125
25
40
应用比例的意义或者基本性质,判断下面的两个比能不能组成比例。
6∶9 和 9∶12
比例的意义:
比例的基本性质:
所以: 6∶9 和 9∶12
不能组成比例。
因为: 6 ∶ 9 =
9∶12 =
≠
因为: 6 × 12 = 72
9 × 9 = 81
所以: 6∶9 和 9∶12
不能组成比例。
72 ≠ 81
比和比例有什么区别?
比
比例
意义
两个数相除又叫做两个数的比。
表示两个比相等式子叫做比例。
构成
由两个数组成,分别叫比的前项和后项。
由四个数组成,两端的两项叫做比例的外项,中间的两项叫做比例的内项。
基本
性质
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
巩固练习:
1、应用比例的基本性质判断下面的比例是否正确:
(1)6 :3 = 8 :5
(2)0.2 :2.5 = 4 :50
(3)2:3 = ︰
1
2
1
3
(4)1.2 :0.6 = 10 :5
(错)
(对)
(错)
(对)
2.我是小法官,对错我来判判。
(1)比例是由任意两个比组成的。 ( )
(2)在比例里,两个内项的积与两个外项的积的差是0。 ( )
(3)比例式中有四个外项,四个内项。( )
×
√
√
3.把握知识点,做题不困难。
(1)( )与 3 : 5 能组成比例。
A. 10:6 B. : C. 30 : 50
(2)( )与 5 : 8 能组成比例。
A. : B. 10:16 C. 3 : 5
(3) 4 : 5 与( ) 能组成比例。
A. : B. 8:10 C. 15 : 12
(4) 7 : 9 与( ) 能组成比例。
A. 70 : 90 B. : C. 3 : 4
1
4
1
5
1
3
1
5
1
5
1
8
1
7
1
9
B
C
B
A
4.一题多变化,动脑解决它:
(1)在比例里,两个内项的积是18,
其中一个外项是2,另一个外项是( )。
(2)如果5a=3b,那么, = ,
=
(3)a︰8=9︰b,那么,a×b=( )
( )
( )
( )
( )
a
b
b
a
9
3
5
5
3
72
思考
下面的四个数可以组成比例吗?把组成的比例
写出来(能写几个写几个).
2、3、4 和 6
因为 2 × 6 = 3 × 4 所以这四个数可以组成比例
2 ∶3 = 4 ∶6
2 ∶4 = 3 ∶6
6 ∶4 = 3 ∶2
6 ∶3 = 4 ∶2
4 ∶2 = 6 ∶3
4 ∶6 = 2 ∶3
3 ∶6 = 2 ∶4
3 ∶2 = 6 ∶4
复习
什么叫做比例?
表示两个比相等的式子叫做比例。
什么叫做比例的基本性质?
在比例里,两个外项的积等于两个内项的积。
判断下列各组比能否组成比例:
⑴ 6 12 和 4 8
和
⑷
:
和
:
⑶
⑵ 24 8 和 0.6 2
:
:
:
:
( )
( )
( )
( )
一个月黑风高的夜晚,一家珠宝店失窃了。第二天早上,小侦探柯南经过仔细勘察,在案发现场发现了一枚犯罪嫌疑人留下的脚印,根据这枚脚印,柯南很快判断出了犯罪嫌疑人的身高,你们知道,他是怎样判断的吗?
侦探柯南之神秘脚印:
解:设罪犯的身高为 x 厘米,
x=25×7
x=175
答:罪犯的身高约是175cm.
侦探柯南之神秘脚印:
科学研究表明:人体身高与脚长的比大约是7:1,柯南在案发现场测得犯罪嫌疑人的脚印长 25 厘米,请你帮忙算一算:这个犯罪嫌疑人的身高约是多少?
:
身高 脚长 = 7 1
:
:
x :25 = 7 : 1
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。
求比例中的未知项,叫做解比例。
1、法国巴黎的埃菲尔铁塔高320m。北京的“世界公园”里有一座埃菲尔铁塔的模型,它的高度与原塔的高度比1:10。这座模型高多少米?
解:设这座模型的高度是X米。
X :320 = 1 :10
10X = 320 × 1
X = 32
320
10
X =
答:这座模型高32米。
1.5
2.5
6
10
汽车厂按1:24的比例生产了一批汽车模型。
轿车模型长24.92cm,
它的实际长度是多少?
公共汽车长11.76m,模型车
的长度是多少?
模型 实际长度 = 1 24
:
:
早上9点钟时,物体的高度与影子的长度
比是5 4,如果这时测得电线杆的影长为4.8
米,那么电线杆的实际长度是多少米?
:
育新小区1号楼的实际高度是
35m,它的高度与模型高度的比是
500:1。模型的高度是多少厘米?
(2)等号左端的比是1.5 ,等号右端比的
前项和后项分别是3.6和4.8。
按照下面的条件列出比例,并且解比例:
:
(1) 和 的比等于 和 的比。
(3)比例的两个内项分别是2和5,两个外项
分别是 和2.5。
:2=5:2.5
:5=2:2.5
2.5:2=5:
2.5:5=2:
: =
:
1.5 : = 3.6 : 4.8
在括号里填上适当的数:
2、0.63 ( )=( ) 10
5
( )
=
8
( )
1、
:
:
5×8 = ( ) ×( )
0.63×10= ( ) ×( )
复习
1、什么叫做比?
两个数相除又叫做两个数的比。
2、什么叫做比值?
比的前项除以比的后项所得的商,叫做比值。
3、什么叫做比的基本性质?
比的前项和后项同时乘或者除以相同
的数(0 除外),比值不变。
口算下面各比的值,哪些比的比值相等?
12 : 16
5 : 3
10 : 6
9 : 15
操场上的国旗: 2.4 : 1.6 =
教室里的国旗: 60 : 40 =
2.4m
1.6m
操场上的国旗
40cm
60cm
教室里的国旗
2.4︰1.6
求出它们的比值,你发现了什么?
60︰40
=
=
或
表示两个比相等的式子叫做比例。
比例有两种表达的形式可以用比号连接也可以用分数线连接
判断两个比能不能组成比例,要看它们的比值是否相等。
判断下面的两个比能不能组成比例.
6∶10 和 9∶15
3
1
︰
2
1
6
︰
4
和
6∶10 和 9∶15
所以 6∶10 和 9∶15
能组成比例.
因为 6∶10 =
3
5
9∶15 =
3
5
=
3
5
3
5
3
1
︰
2
1
6
︰
4
和
3
1
︰2 =
因为
1
6
︰4 =
1
6
1
24
1
6
≠
1
24
所以
不能组成比例。
3
1
︰
2
1
6
︰
4
和
做一做
填空
如果两个比的比值相等,那么这两个比就( )比例.
一个比例,等号左边的比和等号右边的比一定是( )的.
能组成
相等
2cm
4cm
1.5cm
3cm
用右图中的4个数据可以组成多少个比例?
3∶1.5 = 4∶2
3∶4 = 1.5∶2
1.5∶3 = 2∶4
4∶3 = 2∶1.5
2.4 ︰1.6
60 ︰ 40
=
内项
外项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
指出下面比例的外项和内项.
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
做一做
∶
=
6 ∶4
外项
外项
内项
内项
外项
内项
2.4 ︰ 1.6
60 ︰40
=
外项
内项
内项积是:
1.6 × 60=96
外项积是:
2.4 × 40 = 96
2.4
40
1.6
60
×
×
=
计算下面比例的外项积和内项积.
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
做一做
∶
=
6 ∶4
0.6 ∶0.2
∶
=
4.5 × 6 = 27
外项积:
内项积:
外项积:
内项积:
外项积:
内项积:
外项积:
内项积:
2.7 × 10 = 27
6 × 15 = 90
10 × 9 = 90
× 4 = 2
× 6 = 2
0.6 ×
= 0.15
0.2 ×
= 0.15
2.4︰1.6 = 60︰40
在比例里,两个外项的积等于两个内项的积。
交叉相乘
2.4×40=1.6×60
2.4
1.6
=
60
40
比例的基本性质
应用比例的基本性质,判断下面两个比能不能组成比例。
0.2∶2.5 和 4∶50
因为 0.2 × 50 = 10
2.5 × 4 = 10
所以 0.2∶2.5 和4∶50 能组成比例。
10 = 10
1.2∶ 和 ∶5
因为 1.2 × 5 = 6
× =
6≠
所以 1.2∶ 和 ∶5
不能组成比例。
0.5×2 =( )×( )
0.5
5
=
0.2
2
2
5
︰
1
2
=
3
5
︰
3
4
× =( )×( )
2
5
3
4
8︰25=40︰125
( )×( ) =( )×( )
试一试
5
0.2
1
2
3
5
8
125
25
40
应用比例的意义或者基本性质,判断下面的两个比能不能组成比例。
6∶9 和 9∶12
比例的意义:
比例的基本性质:
所以: 6∶9 和 9∶12
不能组成比例。
因为: 6 ∶ 9 =
9∶12 =
≠
因为: 6 × 12 = 72
9 × 9 = 81
所以: 6∶9 和 9∶12
不能组成比例。
72 ≠ 81
比和比例有什么区别?
比
比例
意义
两个数相除又叫做两个数的比。
表示两个比相等式子叫做比例。
构成
由两个数组成,分别叫比的前项和后项。
由四个数组成,两端的两项叫做比例的外项,中间的两项叫做比例的内项。
基本
性质
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
巩固练习:
1、应用比例的基本性质判断下面的比例是否正确:
(1)6 :3 = 8 :5
(2)0.2 :2.5 = 4 :50
(3)2:3 = ︰
1
2
1
3
(4)1.2 :0.6 = 10 :5
(错)
(对)
(错)
(对)
2.我是小法官,对错我来判判。
(1)比例是由任意两个比组成的。 ( )
(2)在比例里,两个内项的积与两个外项的积的差是0。 ( )
(3)比例式中有四个外项,四个内项。( )
×
√
√
3.把握知识点,做题不困难。
(1)( )与 3 : 5 能组成比例。
A. 10:6 B. : C. 30 : 50
(2)( )与 5 : 8 能组成比例。
A. : B. 10:16 C. 3 : 5
(3) 4 : 5 与( ) 能组成比例。
A. : B. 8:10 C. 15 : 12
(4) 7 : 9 与( ) 能组成比例。
A. 70 : 90 B. : C. 3 : 4
1
4
1
5
1
3
1
5
1
5
1
8
1
7
1
9
B
C
B
A
4.一题多变化,动脑解决它:
(1)在比例里,两个内项的积是18,
其中一个外项是2,另一个外项是( )。
(2)如果5a=3b,那么, = ,
=
(3)a︰8=9︰b,那么,a×b=( )
( )
( )
( )
( )
a
b
b
a
9
3
5
5
3
72
思考
下面的四个数可以组成比例吗?把组成的比例
写出来(能写几个写几个).
2、3、4 和 6
因为 2 × 6 = 3 × 4 所以这四个数可以组成比例
2 ∶3 = 4 ∶6
2 ∶4 = 3 ∶6
6 ∶4 = 3 ∶2
6 ∶3 = 4 ∶2
4 ∶2 = 6 ∶3
4 ∶6 = 2 ∶3
3 ∶6 = 2 ∶4
3 ∶2 = 6 ∶4
复习
什么叫做比例?
表示两个比相等的式子叫做比例。
什么叫做比例的基本性质?
在比例里,两个外项的积等于两个内项的积。
判断下列各组比能否组成比例:
⑴ 6 12 和 4 8
和
⑷
:
和
:
⑶
⑵ 24 8 和 0.6 2
:
:
:
:
( )
( )
( )
( )
一个月黑风高的夜晚,一家珠宝店失窃了。第二天早上,小侦探柯南经过仔细勘察,在案发现场发现了一枚犯罪嫌疑人留下的脚印,根据这枚脚印,柯南很快判断出了犯罪嫌疑人的身高,你们知道,他是怎样判断的吗?
侦探柯南之神秘脚印:
解:设罪犯的身高为 x 厘米,
x=25×7
x=175
答:罪犯的身高约是175cm.
侦探柯南之神秘脚印:
科学研究表明:人体身高与脚长的比大约是7:1,柯南在案发现场测得犯罪嫌疑人的脚印长 25 厘米,请你帮忙算一算:这个犯罪嫌疑人的身高约是多少?
:
身高 脚长 = 7 1
:
:
x :25 = 7 : 1
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。
求比例中的未知项,叫做解比例。
1、法国巴黎的埃菲尔铁塔高320m。北京的“世界公园”里有一座埃菲尔铁塔的模型,它的高度与原塔的高度比1:10。这座模型高多少米?
解:设这座模型的高度是X米。
X :320 = 1 :10
10X = 320 × 1
X = 32
320
10
X =
答:这座模型高32米。
1.5
2.5
6
10
汽车厂按1:24的比例生产了一批汽车模型。
轿车模型长24.92cm,
它的实际长度是多少?
公共汽车长11.76m,模型车
的长度是多少?
模型 实际长度 = 1 24
:
:
早上9点钟时,物体的高度与影子的长度
比是5 4,如果这时测得电线杆的影长为4.8
米,那么电线杆的实际长度是多少米?
:
育新小区1号楼的实际高度是
35m,它的高度与模型高度的比是
500:1。模型的高度是多少厘米?
(2)等号左端的比是1.5 ,等号右端比的
前项和后项分别是3.6和4.8。
按照下面的条件列出比例,并且解比例:
:
(1) 和 的比等于 和 的比。
(3)比例的两个内项分别是2和5,两个外项
分别是 和2.5。
:2=5:2.5
:5=2:2.5
2.5:2=5:
2.5:5=2:
: =
:
1.5 : = 3.6 : 4.8
在括号里填上适当的数:
2、0.63 ( )=( ) 10
5
( )
=
8
( )
1、
:
:
5×8 = ( ) ×( )
0.63×10= ( ) ×( )
