人教版(五四制)数学七上 12.4 平移 课件 (共36张ppt)
文档属性
| 名称 | 人教版(五四制)数学七上 12.4 平移 课件 (共36张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-19 18:33:38 | ||
图片预览









文档简介
12.4 平移
请举出生活中你认为是“平移”的例子.
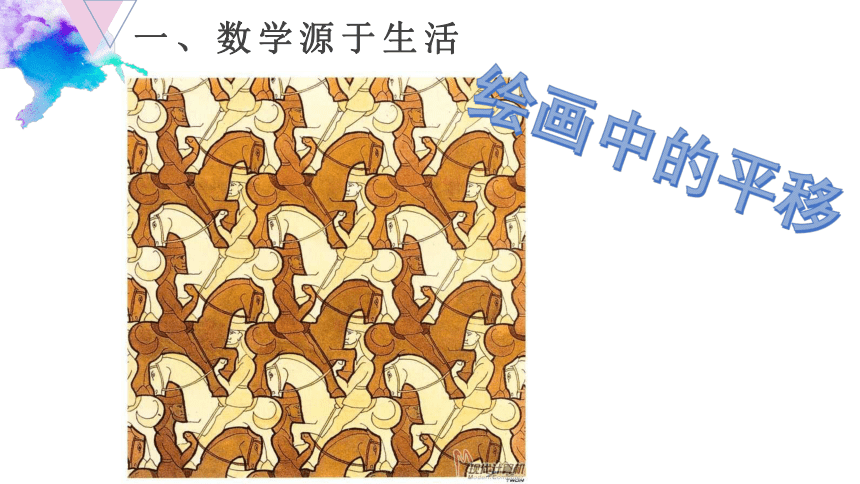
一、数学源于生活
绘画中的平移
一、数学源于生活
绘画中的平移
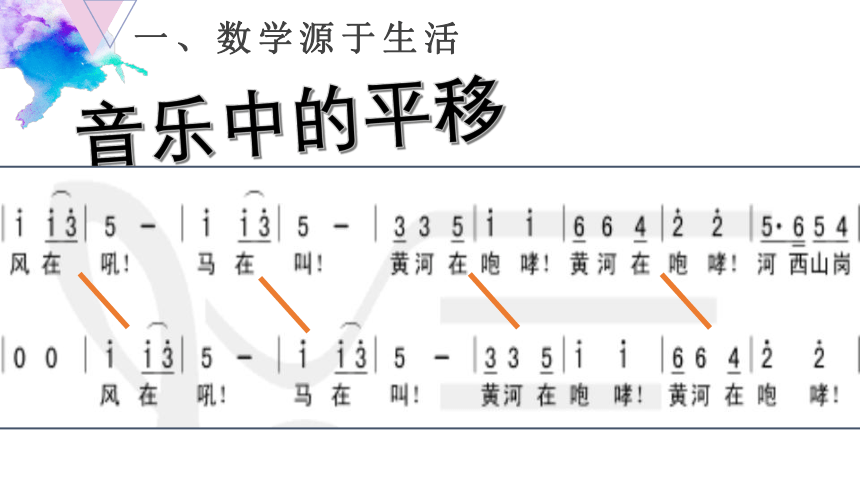
一、数学源于生活
音乐中的平移
一、数学源于生活
一、数学源于生活
一、数学源于生活
传统文化中的平移
一、数学源于生活
一、数学源于生活
学习目标
重点
难点
1、认识平移,了解平移的性质。
2、能按要求作出简单平面图形的平移图形。
3、能够利用平移的知识解决问题。
对平移的理解和应用
对平移性质的探究
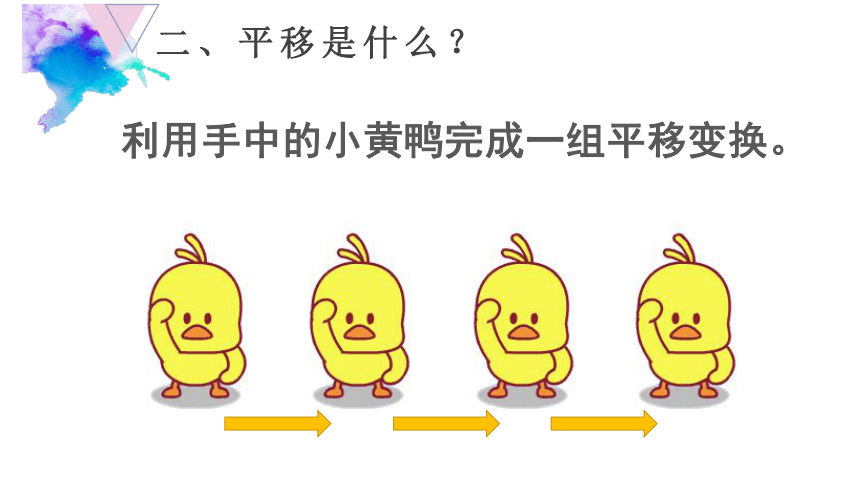
利用手中的小黄鸭完成一组平移变换。
二、平移是什么?
体会移动的过程,
我们来定义“平移”吧!
把一个图形整体沿某一直线方向移动一定的距离。图形的这种移动,就叫做平移。
总结归纳
二、平移是什么?
探究:平移的要素
平移的要素:
平移的方向
平移的距离
总结归纳
二、平移是什么?
跟踪练习:
1、下列生活中的各个现象,属于平移的是( )
A.拉开抽屉 B.用放大镜看文字
C.时钟上分针的运动 D.你和平面镜中的像
A
二、平移是什么?
跟踪练习:
2、下列车标图案哪些是利用平移来设计的?(不记颜色)
(1)
(2)
(3)
(4)
(5)
(6)
?
√
?
√
?
?
二、平移是什么?
跟踪练习:
3、下列图形中,是由(1)仅通过平移得到的是( )
C
二、平移是什么?
思考
平移过程中,什么发生了变化?什么没变?
三、平移的性质
性质1:
平移前后两图形形状和大小完全相同。
三、平移的性质
总结归纳
在相邻两个小黄鸭中,找出三组对应点(例如,它们的右眼A与A’)连接这些对应点。
猜想三组对应点的连线有什么特殊关系?
三、平移的性质
小组合作探究,验证一下你们的猜想。
位置关系:
数量关系:
AA’∥BB’∥CC’ (平行)
AA’=BB’=CC’ (相等)
三、平移的性质
(或在同一条直线上)
三、平移的性质
位置关系:
数量关系:
AA’∥BB’∥CC’ (平行)
AA’=BB’=CC’ (相等)
性质2:
平移前后两图形对应点的连线平行(或在同一条直线上)且相等。
三、平移的性质
总结归纳
学以致用
例、如图,平移三角形ABC,使点A移动到点A’,画出平移后的三角形A’B’C’.
四、应用性质作图
跟踪练习
如图,在方格纸中平移三角形ABC,使点A移到点M,点B和点C应移到什么位置?在将点A由点M移到点N,分别画出两次平移后的三角形,如果直接平移三角形ABC,使点A移到点N,它和我们前面得到的三角形位置相同吗?
四、应用性质作图
1、某宾馆打算在大厅的楼梯上铺红地毯,楼梯侧面如图所示。需要购买 米地毯。
3+6=9(米)
9
五、数学服务生活
变式:某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
D
五、数学服务生活
2、如图,在宽为10 m,长为40 m的长方形菜地上有两条小路,小路宽度为1 m,这块菜地的面积为 。
10?1×40?1=351(????2)
?
五、数学服务生活
????????????????
?
变式:如图,一块长为8m的正方形土地,上面修了横竖各两条道路,宽都是1m,空白的部分种上各种花草,请利用平移的知识求出种花草的面积为 。
五、数学服务生活
????????????
?
3、如图,△A’B’C’是由△ABC沿射线AC方向平移2 cm得到,若AC=3 cm,则A’C=_______.
2cm
六、利用平移解题
变式:如图,三角形ABC向右平移2个单位长度得到三角形DEF,已知三角形ABC的周长为10,则四边形ABFD的周长为 .
六、利用平移解题
如图,将直角三角形ABC沿BC方向平移得直角三角形DEF,其中AB=8,BE=10,DM=4,求阴影部分的面积。
七、拓展延伸
把一个图形整体沿某一直线方向移动一定的距离。图形的这种移动,就叫做平移。
小结
定义:
性质:
1、平移前后两图形形状和大小完全相同。
小结
2、平移前后两图形对应点的连线平行(或在同一条直线上)且相等。
应用:
1、利用平移的性质作图
(注意平移的距离和平移的方向)
2、解决实际问题
小结
希望“平移”知识能够给同学们的学习和生活增添灵感和快乐!
谢谢
请举出生活中你认为是“平移”的例子.
一、数学源于生活
绘画中的平移
一、数学源于生活
绘画中的平移
一、数学源于生活
音乐中的平移
一、数学源于生活
一、数学源于生活
一、数学源于生活
传统文化中的平移
一、数学源于生活
一、数学源于生活
学习目标
重点
难点
1、认识平移,了解平移的性质。
2、能按要求作出简单平面图形的平移图形。
3、能够利用平移的知识解决问题。
对平移的理解和应用
对平移性质的探究
利用手中的小黄鸭完成一组平移变换。
二、平移是什么?
体会移动的过程,
我们来定义“平移”吧!
把一个图形整体沿某一直线方向移动一定的距离。图形的这种移动,就叫做平移。
总结归纳
二、平移是什么?
探究:平移的要素
平移的要素:
平移的方向
平移的距离
总结归纳
二、平移是什么?
跟踪练习:
1、下列生活中的各个现象,属于平移的是( )
A.拉开抽屉 B.用放大镜看文字
C.时钟上分针的运动 D.你和平面镜中的像
A
二、平移是什么?
跟踪练习:
2、下列车标图案哪些是利用平移来设计的?(不记颜色)
(1)
(2)
(3)
(4)
(5)
(6)
?
√
?
√
?
?
二、平移是什么?
跟踪练习:
3、下列图形中,是由(1)仅通过平移得到的是( )
C
二、平移是什么?
思考
平移过程中,什么发生了变化?什么没变?
三、平移的性质
性质1:
平移前后两图形形状和大小完全相同。
三、平移的性质
总结归纳
在相邻两个小黄鸭中,找出三组对应点(例如,它们的右眼A与A’)连接这些对应点。
猜想三组对应点的连线有什么特殊关系?
三、平移的性质
小组合作探究,验证一下你们的猜想。
位置关系:
数量关系:
AA’∥BB’∥CC’ (平行)
AA’=BB’=CC’ (相等)
三、平移的性质
(或在同一条直线上)
三、平移的性质
位置关系:
数量关系:
AA’∥BB’∥CC’ (平行)
AA’=BB’=CC’ (相等)
性质2:
平移前后两图形对应点的连线平行(或在同一条直线上)且相等。
三、平移的性质
总结归纳
学以致用
例、如图,平移三角形ABC,使点A移动到点A’,画出平移后的三角形A’B’C’.
四、应用性质作图
跟踪练习
如图,在方格纸中平移三角形ABC,使点A移到点M,点B和点C应移到什么位置?在将点A由点M移到点N,分别画出两次平移后的三角形,如果直接平移三角形ABC,使点A移到点N,它和我们前面得到的三角形位置相同吗?
四、应用性质作图
1、某宾馆打算在大厅的楼梯上铺红地毯,楼梯侧面如图所示。需要购买 米地毯。
3+6=9(米)
9
五、数学服务生活
变式:某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
D
五、数学服务生活
2、如图,在宽为10 m,长为40 m的长方形菜地上有两条小路,小路宽度为1 m,这块菜地的面积为 。
10?1×40?1=351(????2)
?
五、数学服务生活
????????????????
?
变式:如图,一块长为8m的正方形土地,上面修了横竖各两条道路,宽都是1m,空白的部分种上各种花草,请利用平移的知识求出种花草的面积为 。
五、数学服务生活
????????????
?
3、如图,△A’B’C’是由△ABC沿射线AC方向平移2 cm得到,若AC=3 cm,则A’C=_______.
2cm
六、利用平移解题
变式:如图,三角形ABC向右平移2个单位长度得到三角形DEF,已知三角形ABC的周长为10,则四边形ABFD的周长为 .
六、利用平移解题
如图,将直角三角形ABC沿BC方向平移得直角三角形DEF,其中AB=8,BE=10,DM=4,求阴影部分的面积。
七、拓展延伸
把一个图形整体沿某一直线方向移动一定的距离。图形的这种移动,就叫做平移。
小结
定义:
性质:
1、平移前后两图形形状和大小完全相同。
小结
2、平移前后两图形对应点的连线平行(或在同一条直线上)且相等。
应用:
1、利用平移的性质作图
(注意平移的距离和平移的方向)
2、解决实际问题
小结
希望“平移”知识能够给同学们的学习和生活增添灵感和快乐!
谢谢
