人教版(五四制)数学七上 12.4 平移 课件 (共24张ppt)
文档属性
| 名称 | 人教版(五四制)数学七上 12.4 平移 课件 (共24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-19 18:36:57 | ||
图片预览





文档简介
授课教师:
12.4 平 移
(人教版五.四学制 七年级上)
观察
思考
观察
思考
平
移
平
移
课堂
练习
生活
例子
生活
例子
课堂
练习
归纳
总结
探究
新知
归纳
总结
探究
新知
小结
回顾
学习目标:
掌握平移的概念,发现并归纳平移的性质。
学会利用平移绘制某些特殊的图案。
3.如何运用平移的性质解决问题。
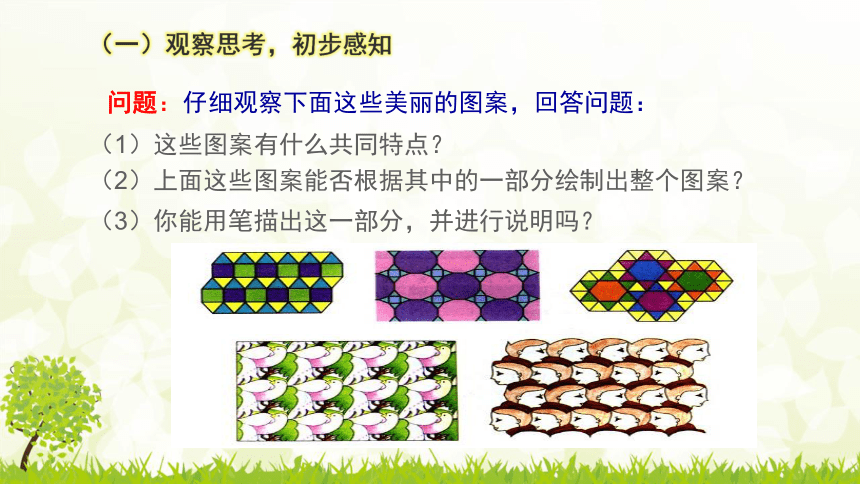
问题:仔细观察下面这些美丽的图案,回答问题:
(1)这些图案有什么共同特点?
(2)上面这些图案能否根据其中的一部分绘制出整个图案?
(一)观察思考,初步感知
(3)你能用笔描出这一部分,并进行说明吗?
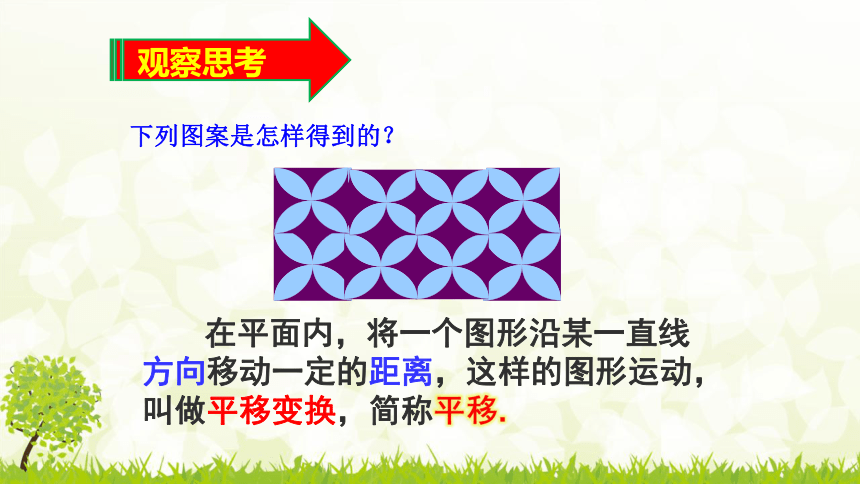
下列图案是怎样得到的?
观察思考
在平面内,将一个图形沿某一直线方向移动一定的距离,这样的图形运动,叫做平移变换,简称平移.
探究:你认为如何在一张纸上画出一排和课本第64页图12.4-2形状、大小都一样的雪人呢?
导学:小组讨论,解决以下问题:
①雪人的形状、大小、位置在运动前后是否发生变化?
②相应的点是运动到了什么位置?
③连接几组对应点,观察得到的线段,它们的位置、长短有什么关系?
时间: 预设3分钟
(二)动手操作,探索平移特征
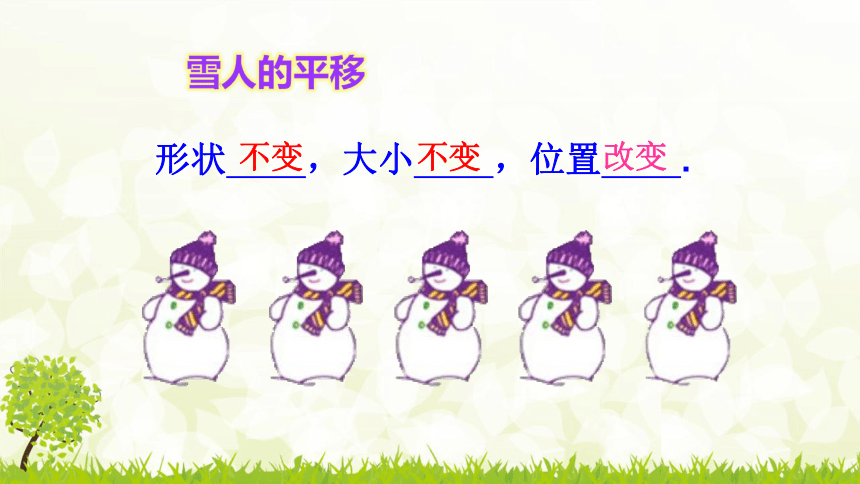
形状 ,大小 ,位置 .
不变
不变
改变
雪人的平移
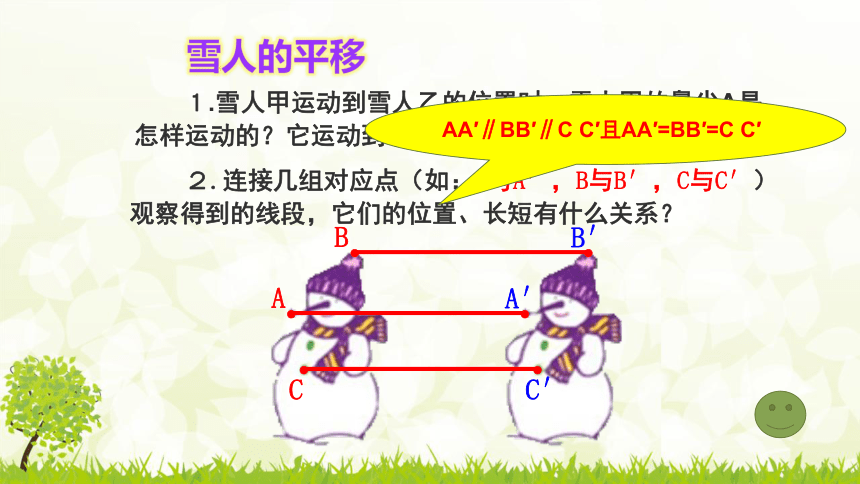
2.连接几组对应点(如:A与A′,B与B′,C与C′)观察得到的线段,它们的位置、长短有什么关系?
1.雪人甲运动到雪人乙的位置时,雪人甲的鼻尖A是怎样运动的?它运动到了什么位置?帽顶B呢?纽扣C呢?
雪人的平移
A
A′
C
B
C′
B′
AA′∥BB′∥C C′且AA′=BB′=C C′
请根据你的生活和学习经验, 列举一些生活中的平移现象.
(三)联系生活 提高认识
楼房也能移
近日,上海浦东新区一栋百岁高龄,砖木结构的老洋房开始实施整体平移。在平移工程中,千斤顶在计算机的控制下将使整栋大楼“行走”30多米,行走路线为“L”型
3.下图中的变换属于平移的有哪些?
A
B
D
E
C
F
(四)运用新知 深化理解
1.图形经过平移后,( )图形的位置,( )图形的形状,( )图形的大小。(填“改变”或“不改变”)
2.图形的平移由( )和( )决定的.
在方格纸中,把ΔABC向右平移6格,画出所得到的像ΔA’B’C’.
(1)线段AA’, BB’, CC’ 之间有什么关系呢?
AA’=BB’=CC’ 且AA’//BB’//CC’
连接对应点的线段平行且相等。
(2)观察ΔABC与ΔA’B’C’的边、角的大小,你发现了什么?
得:AB=A’B’, BC=B’C’, AC=A’C’
∠A= ∠A’,∠B= ∠B’ ,∠C= ∠C’
A
B
C
A’
C’
B’
平移变换不改变图形的形状、大小和方向.
主动探究 总结性质
经过平移,△ABC的顶点A移到了点D(如图所示),试画出平移后的三角形。
A
B
C
D
F
E
步 骤:
1.定方向定距离:连接 AD;
2.利用平移的性质找到B、C的对应点E、F;
3.分别连接DE、DF、EF.
例题
空间几何体的平移:
探究
点的平移:
线的平移:
平面图形的平移:
今日重点
2.平移的特征:
(1)只改变位置,不改变方向和大小.
(2)对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行(或在同一直线上)且相等.
3.平移的两要素:方向和距离.
1.平移的定义:
在平面内,将一个图形沿某一直线方向移动一定的距离,这样的图形运动,叫做平移变换,简称平移.
下列汽车标志哪些是利用平移设计的?(不考虑颜色)
(1)
(6)
(5)
(4)
(3)
(2)
(7)
√
√
√
巩固
如图,在高为2米,水平距离为3米楼梯的表面铺地毯,地毯的长度至少需多少米?
学以致用
如图,某小区规划在一个长为AD=120米,宽为AB=30米的小路,其中两条与AB平行,另一条与AD平行,其余部分种花,若种花的每平方米的造价是30元,你核算下共需资金多少元?
中考连线
A
B
C
D
如图,在一块长为20m,宽为8m的长方形的草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是0.5m).请你猜想草地的面积是多少.
(20 – 0.5) ×8=156m2
中考连线
欣赏
今日作业
用平移方法怎样得出平行四边形面积公式
S = ah
a
h
今日作业
用平移方法怎样得出平行四边形面积公式
S = ah
a
教师寄语:
人生的价值,改变的是时间,不变的是态度和目标。耕耘和收获是平行且相等的。
12.4 平 移
(人教版五.四学制 七年级上)
观察
思考
观察
思考
平
移
平
移
课堂
练习
生活
例子
生活
例子
课堂
练习
归纳
总结
探究
新知
归纳
总结
探究
新知
小结
回顾
学习目标:
掌握平移的概念,发现并归纳平移的性质。
学会利用平移绘制某些特殊的图案。
3.如何运用平移的性质解决问题。
问题:仔细观察下面这些美丽的图案,回答问题:
(1)这些图案有什么共同特点?
(2)上面这些图案能否根据其中的一部分绘制出整个图案?
(一)观察思考,初步感知
(3)你能用笔描出这一部分,并进行说明吗?
下列图案是怎样得到的?
观察思考
在平面内,将一个图形沿某一直线方向移动一定的距离,这样的图形运动,叫做平移变换,简称平移.
探究:你认为如何在一张纸上画出一排和课本第64页图12.4-2形状、大小都一样的雪人呢?
导学:小组讨论,解决以下问题:
①雪人的形状、大小、位置在运动前后是否发生变化?
②相应的点是运动到了什么位置?
③连接几组对应点,观察得到的线段,它们的位置、长短有什么关系?
时间: 预设3分钟
(二)动手操作,探索平移特征
形状 ,大小 ,位置 .
不变
不变
改变
雪人的平移
2.连接几组对应点(如:A与A′,B与B′,C与C′)观察得到的线段,它们的位置、长短有什么关系?
1.雪人甲运动到雪人乙的位置时,雪人甲的鼻尖A是怎样运动的?它运动到了什么位置?帽顶B呢?纽扣C呢?
雪人的平移
A
A′
C
B
C′
B′
AA′∥BB′∥C C′且AA′=BB′=C C′
请根据你的生活和学习经验, 列举一些生活中的平移现象.
(三)联系生活 提高认识
楼房也能移
近日,上海浦东新区一栋百岁高龄,砖木结构的老洋房开始实施整体平移。在平移工程中,千斤顶在计算机的控制下将使整栋大楼“行走”30多米,行走路线为“L”型
3.下图中的变换属于平移的有哪些?
A
B
D
E
C
F
(四)运用新知 深化理解
1.图形经过平移后,( )图形的位置,( )图形的形状,( )图形的大小。(填“改变”或“不改变”)
2.图形的平移由( )和( )决定的.
在方格纸中,把ΔABC向右平移6格,画出所得到的像ΔA’B’C’.
(1)线段AA’, BB’, CC’ 之间有什么关系呢?
AA’=BB’=CC’ 且AA’//BB’//CC’
连接对应点的线段平行且相等。
(2)观察ΔABC与ΔA’B’C’的边、角的大小,你发现了什么?
得:AB=A’B’, BC=B’C’, AC=A’C’
∠A= ∠A’,∠B= ∠B’ ,∠C= ∠C’
A
B
C
A’
C’
B’
平移变换不改变图形的形状、大小和方向.
主动探究 总结性质
经过平移,△ABC的顶点A移到了点D(如图所示),试画出平移后的三角形。
A
B
C
D
F
E
步 骤:
1.定方向定距离:连接 AD;
2.利用平移的性质找到B、C的对应点E、F;
3.分别连接DE、DF、EF.
例题
空间几何体的平移:
探究
点的平移:
线的平移:
平面图形的平移:
今日重点
2.平移的特征:
(1)只改变位置,不改变方向和大小.
(2)对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行(或在同一直线上)且相等.
3.平移的两要素:方向和距离.
1.平移的定义:
在平面内,将一个图形沿某一直线方向移动一定的距离,这样的图形运动,叫做平移变换,简称平移.
下列汽车标志哪些是利用平移设计的?(不考虑颜色)
(1)
(6)
(5)
(4)
(3)
(2)
(7)
√
√
√
巩固
如图,在高为2米,水平距离为3米楼梯的表面铺地毯,地毯的长度至少需多少米?
学以致用
如图,某小区规划在一个长为AD=120米,宽为AB=30米的小路,其中两条与AB平行,另一条与AD平行,其余部分种花,若种花的每平方米的造价是30元,你核算下共需资金多少元?
中考连线
A
B
C
D
如图,在一块长为20m,宽为8m的长方形的草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是0.5m).请你猜想草地的面积是多少.
(20 – 0.5) ×8=156m2
中考连线
欣赏
今日作业
用平移方法怎样得出平行四边形面积公式
S = ah
a
h
今日作业
用平移方法怎样得出平行四边形面积公式
S = ah
a
教师寄语:
人生的价值,改变的是时间,不变的是态度和目标。耕耘和收获是平行且相等的。
