人教版数学 八年级上册13.1轴对称教案
图片预览



文档简介
轴对称
一、目标与策略
明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!
学习目标:
通过具体实例认识轴对称,探索它的基本性质,理解对应点所连的线段被对称轴垂直平分的性质;
能按要求作出简单平面图形经过一次或两次轴对称后的图形;
探索简单图形之间的轴对称关系,并能指出对称轴;
欣赏生活中的轴对称图形,结合现实生活中的典型实例了解并欣赏物体的镜面对称.
重点:
轴对称概念及有关性质;
基本图形(如线段、角)的轴对称性;
画和轴对称有关的图形.
难点:
轴对称的性质的探索和掌握.
学习策略:
通过操作、归纳,探索并总结出轴对称的性质及线段垂直平分线的性质,并能运用其性质解答简单的几何问题.
二、学习与应用
(
“凡事预则立,不预则废”
.
科学地预习才能使我们上课听讲更有目的性和针对性
.
我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记
.
)
(
知识回顾
——
复习
学习新知识之前,看看你的知识贮备过关了吗?
)
(一)能够完全重合的两个图形叫
.
(二)能够完全重合的两个三角形叫
.
(三)两个全等三角形重合在一起,重合的顶点叫
,重合的边叫
,重合的角叫
.
(四)全等三角形对应边
,对应角
.
(五)在线段上并且能够把这条线段平分点的点叫做
.
(
知识要点——预习和课堂学习
认真阅读、理解教材,尝试把下列知识要点内容补充完整,带着自己预习的疑惑认真听课学习
.请在虚线部分填写预习内容,在实线部分填写课堂学习内容.课堂笔记或者
其它补充填在右栏
.
)
知识点一:轴对称图形及对称轴
(一)轴对称图形:一个图形沿着某直线折叠,直线两旁的部分能完全重合,这个图形就叫做
,该直线就是它的
.
(二)要点:前提是
个图形,且这个图形满足两个条件:
(1)存在直线(对称轴);
(2)沿着这条直线折叠,折痕两旁的部分能
.
(三)注意:一个轴对称图形的对称轴是
且不一定只有一条,可能有两条或多条.
如图所示:
知识点二:轴对称及对称点
(一)轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个
重合,那么就说这两个图形关于这条直线
(或说这两个图形成轴对称),这条直线叫做
.折叠后重合的点是
,也叫做对称点.
(二)要点:
(1)前提是
个图形;
(2)存在一条直线;
(3)两个图形沿着这条直线对折能够完全重合.
(三)注意:
(1)成轴对称的两个图形一定全等;
(2)它与轴对称图形的区别主要是:它是指
个图形,而轴对称图形前提是
个图形;
(3)成轴对称的两个图形除了全等外还有特定的位置关系.如图所示:
知识点三:轴对称与轴对称图形
(一)相互转化:
轴对称图形和轴对称的关系非常密切,若把成轴对称的两个图形看作一个整体,则这个整体就是
;反过来,若把轴对称图形的对称轴两旁的部分看作两个图形,则这两个图形关于这条直线(原对称轴)
.
(二)轴对称、轴对称图形的性质
(1)性质1:若两个图形关于某直线对称,那么对称轴是
;
注:经过线段
并且
于这条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线.
性质1的证明如下:
如图所示,△ABC与△关于l对称,其中点A、是对称点,设交对称轴于点P.将△ABC和△沿l折叠后,点A与重合,则有,∠1=∠2=90°,即对称轴把垂直平分,同样也能把、都垂直平分,于是得出性质1.
(2)性质2:轴对称图形的对称轴也是
.
证明类似性质1.
(3)小结:不论性质1,还是性质2所指的都是只要两个点关于某直线对称,那么这条直线(对称轴)就是这两个点连线的
.也就是说这两条性质所体现的是
与
的关系.也揭示了轴对称(轴对称图形)的实质.
知识点四:线段的垂直平分线
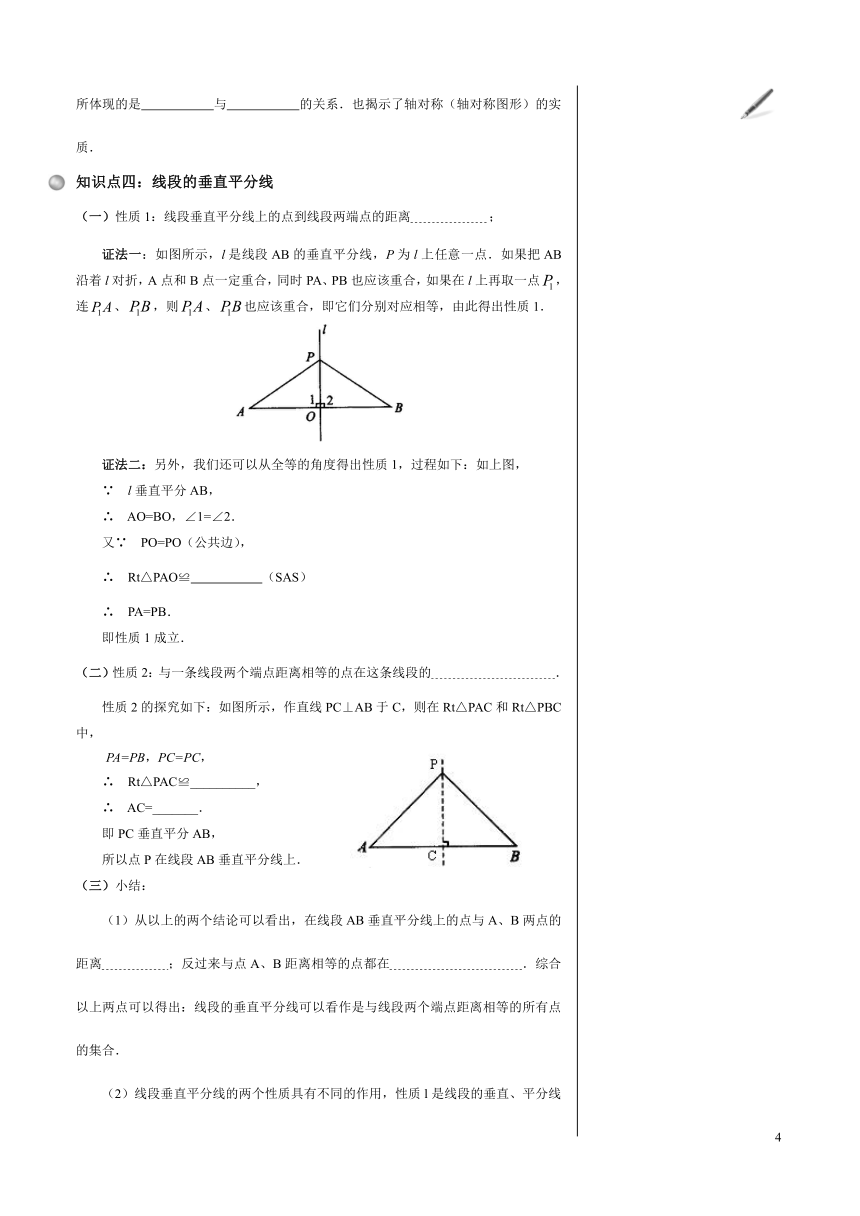
(一)性质1:线段垂直平分线上的点到线段两端点的距离
;
证法一:如图所示,l是线段AB的垂直平分线,P为l上任意一点.如果把AB沿着l对折,A点和B点一定重合,同时PA、PB也应该重合,如果在l上再取一点,连、,则、也应该重合,即它们分别对应相等,由此得出性质1.
证法二:另外,我们还可以从全等的角度得出性质1,过程如下:如上图,
∵
l垂直平分AB,
∴
AO=BO,∠1=∠2.
又∵
PO=PO(公共边),
∴
Rt△PAO≌
(SAS)
∴
PA=PB.
即性质1成立.
(二)性质2:与一条线段两个端点距离相等的点在这条线段的
.
性质2的探究如下:如图所示,作直线PC⊥AB于C,则在Rt△PAC和Rt△PBC中,
PA=PB,PC=PC,
∴
Rt△PAC≌__________,
∴
AC=_______.
即PC垂直平分AB,
所以点P在线段AB垂直平分线上.
(三)小结:
(1)从以上的两个结论可以看出,在线段AB垂直平分线上的点与A、B两点的距离
;反过来与点A、B距离相等的点都在
.综合以上两点可以得出:线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.
(2)线段垂直平分线的两个性质具有不同的作用,性质l是线段的垂直、平分线的性质,可用它来证明线段
的问题;而性质2实质是
的判定.
知识点五:对称轴的作法
(一)若两个图形成轴对称,其对称轴就是任何一对对应点所连线段的
.
因此只要找到一对对应点,再作出连接它们的线段的
就可以得到这两个图形的对称轴.轴对称图形的对称轴作法相同.
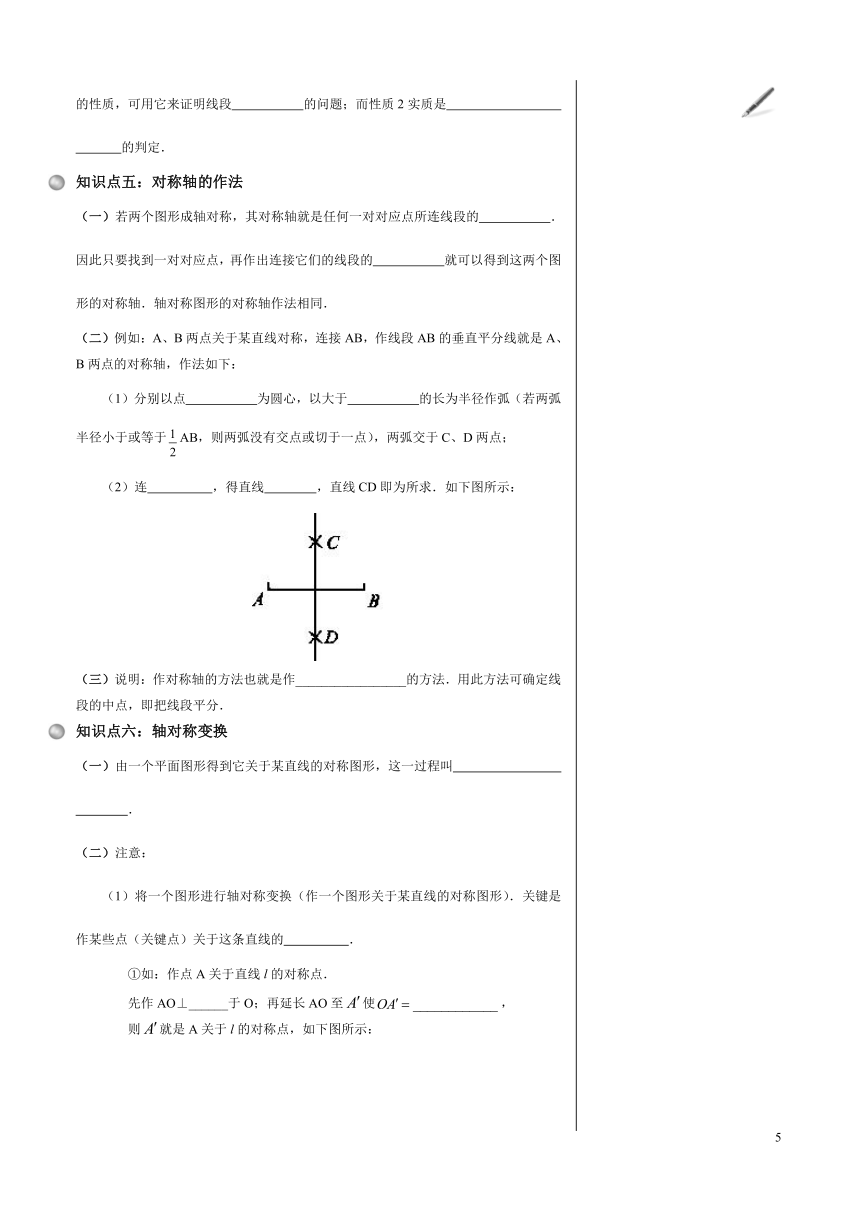
(二)例如:A、B两点关于某直线对称,连接AB,作线段AB的垂直平分线就是A、B两点的对称轴,作法如下:
(1)分别以点
为圆心,以大于
的长为半径作弧(若两弧
半径小于或等于AB,则两弧没有交点或切于一点),两弧交于C、D两点;
(2)连
,得直线
,直线CD即为所求.如下图所示:
(三)说明:作对称轴的方法也就是作_________________的方法.用此方法可确定线段的中点,即把线段平分.
知识点六:轴对称变换
(一)由一个平面图形得到它关于某直线的对称图形,这一过程叫
.
(二)注意:
(1)将一个图形进行轴对称变换(作一个图形关于某直线的对称图形).关键是作某些点(关键点)关于这条直线的
.
①如:作点A关于直线l的对称点.
先作AO⊥______于O;再延长AO至使,
则就是A关于l的对称点,如下图所示:
②主要有两步:第一步,过已知点作对称轴的
,得到一个垂线段;第二步,将这个垂线段延长
所到达的点就是已知点关于这条直线(对称轴)的对称点.
(2)成轴对称的两个图形中的任何一个都可以看作是另一个图形经过轴对称变换得到的.同样,一个轴对称图形也可以看作是以它的一部分为基础,经轴对称变换扩展而成的.
(3)经过轴对称变换并结合平移变换我们可得到一些美丽的图案,如图所示:
知识点七:用坐标表示轴对称
(一)关于x轴对称的两个点的横(纵)坐标的关系
已知P点坐标,则它关于x轴的对称点的坐标为
,如下图所示:
即关于x轴的对称的两点,坐标的关系是:横坐标
,纵坐标互为
.
(二)关于y轴对称的两个点横(纵)坐标的关系
已知P点坐标为,则它关于y轴对称点的坐标为
,如上图所示.
即关于y轴对称的两点坐标关系是:纵坐标
,横坐标互为
.
注意:由此我们可以在平面直角坐标系中作出与一个已知图形关于x轴或y轴对称的图形.
(三)关于与x轴(y轴)平行的直线对称的两个点横(纵)坐标的关系
(1)P点坐标关于直线的对称点的坐标为
.
证明:如下图所示,令坐标为,由题意可知,即,故.所以.
同样可以推导出下面的结论.
(2)P点关于直线的对称点的坐标为
,如上图所示.
(
经典例题-自主学习
认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
.
无星号题目要求同学们必须掌握,为基础题型,一个星号的题目综合性稍强
.
)
类型一:对称轴问题
例1.观察下图中的图案,问这些轴对称图形,各有几条对称轴?
思路点拨:对于一个图形的对称轴一定要按定义全方位地去找或按照定义实际操作一下,否则就容易造成漏解或找不到对称轴.
解:
总结升华:
.
举一反三:
【变式1】试说出下列图形的对称轴的条数.
(1)线段;
(2)角;
(3)平行线(两条).
解析:
类型二:轴对称图形的作法
例2.已知△ABC,直线l.求作,使和△ABC关于l对称.
思路点拨:作一个图形关于已知直线的对称图形关键是作出一些特殊点关于已知直线的对称点,所谓的特殊点,即可以决定图形的大小和形状的点,一般来说一个多边形的特殊点就是它的各个
.
作法:
总结升华:
.
举一反三:
【变式】把图中的图形补成以l为对称轴的轴对称图形.
解析:
类型三:中垂线问题
例3.如图所示,在△ABC中,AC=10cm,AB的中垂线交AB于E,交AC于D,
△DBC的周长为16
cm,求BC的长.
思路点拨:欲求BC长,只需求出DB+DC.而DE垂直平分
,故
,此题可解.
解析:
总结升华:
.
举一反三:
【变式1】如图所示,AD垂直平分BC,DE⊥AB,DF⊥AC,垂足分别为E、F.求证DE=DF.
思路点拨:欲证DE=DF,只需证AD是∠BAC的平分线.而AD是BC中垂线可得B、C两点关于
对称,故△ABD和△ACD关于
对称,则可得∠BAD
=
.
证明:
总结升华:
.
【变式2】如图所示,在道路OA、OB的交叉区域内有M、N两所学校,现在要在此区域内建一图书馆P,使它到两条道路距离相等,并且到两所学校距离也相等,求P点位置.
思路点拨:P点到OA、OB距离相等,只需P在
上即可.
P到M、N距离相等,只需P点在
上即可.
解:
总结升华:
.
类型四:最短路问题
☆☆例4.在锐角∠AOB内有一定点P,试在OA、OB上确定两点C、D,使△PCD的周长最短.
思路点拨:△PCD的周长等于PC+CD+PD,要使△PCD的周长最短,根据两点之间线段最短,只需使得PC+CD+PD的大小等于某两点之间的距离,于是考虑作点P关于直线OA和OB的对称点E、F,则△PCD的周长等于线段EF的长.
解析:
总结升华:
.
举一反三:
【变式】草原上两个居民点A、B在河流a的同旁,一汽车从A出发到B,途中需要到河边加水.汽车在哪一点加水,可使行驶的路程最短?在图上画出该点.
思路点拨:若P为直线a上的点,则要使PA+PB最小与线段有关的结论是两点之间
最短,当把PA+PB转化成为一条线段时,点P就是符合条件的点.
解析:
类型五:坐标系中的对称问题
例5.如图,(1)请写出△ABC中各顶点的坐标.(2)在同一坐标系中画出直线m:x=-1,并作出△ABC关于直线m对称的△A′B′C′.(3)若P(a,b)是△ABC中AC边上一点,请表示其在△A′B′C′中对应点的坐标.
思路点拨:直线m:x=-1表示直线m上任意一点的横坐标都等于
,因此过点(-1,0)作_____轴的平行线即直线m.画出直线m后,再作点A、C关于直线m的对称点A′、C′,而点B在直线m上,则其关于直线m对称的点B′就是
.
解析:
总结升华:
.
举一反三:
【变式】如下图,一束光线从y轴上的点A(0,2)出发,经过x轴上点C反射后经过点B(6,6),则光线从点A到点B所经过的路程是(
)
A.10
B.8
C.6
D.
4
答案:
三、总结与测评
要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力.
(
总结规律和方法
——
强化所学
认真回顾总结本部分内容的规律和方法,熟练掌握技能技巧.
)
(一)由一个平面图形得到它的轴对称图形叫做轴对称变换.成轴对称的两个图形中的任何一个可以看着由另一个图形经过_____________后得到.
(二)轴对称变换的性质:
(1)经过轴对称变换得到的图形与原图形的形状、大小完全一样.
(2)经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的
.
(3)连接任意一对对应点的线段被对称轴
.
(三)作一个图形关于某条直线的轴对称图形的步骤:
(1)作出一些关键点或特殊点的对称点.
(2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形.
(四)点P(x,y)关于x轴对称的点的坐标是
;
点P(x,y)关于y轴对称的点的坐标是
;
点P(x,y)关于原点对称的点的坐标是
.
(五)点P(x,y)关于直线x=m对称的点的坐标是
;
点P(x,y)关于直线y=n对称的点的坐标是
.
14
一、目标与策略
明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!
学习目标:
通过具体实例认识轴对称,探索它的基本性质,理解对应点所连的线段被对称轴垂直平分的性质;
能按要求作出简单平面图形经过一次或两次轴对称后的图形;
探索简单图形之间的轴对称关系,并能指出对称轴;
欣赏生活中的轴对称图形,结合现实生活中的典型实例了解并欣赏物体的镜面对称.
重点:
轴对称概念及有关性质;
基本图形(如线段、角)的轴对称性;
画和轴对称有关的图形.
难点:
轴对称的性质的探索和掌握.
学习策略:
通过操作、归纳,探索并总结出轴对称的性质及线段垂直平分线的性质,并能运用其性质解答简单的几何问题.
二、学习与应用
(
“凡事预则立,不预则废”
.
科学地预习才能使我们上课听讲更有目的性和针对性
.
我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记
.
)
(
知识回顾
——
复习
学习新知识之前,看看你的知识贮备过关了吗?
)
(一)能够完全重合的两个图形叫
.
(二)能够完全重合的两个三角形叫
.
(三)两个全等三角形重合在一起,重合的顶点叫
,重合的边叫
,重合的角叫
.
(四)全等三角形对应边
,对应角
.
(五)在线段上并且能够把这条线段平分点的点叫做
.
(
知识要点——预习和课堂学习
认真阅读、理解教材,尝试把下列知识要点内容补充完整,带着自己预习的疑惑认真听课学习
.请在虚线部分填写预习内容,在实线部分填写课堂学习内容.课堂笔记或者
其它补充填在右栏
.
)
知识点一:轴对称图形及对称轴
(一)轴对称图形:一个图形沿着某直线折叠,直线两旁的部分能完全重合,这个图形就叫做
,该直线就是它的
.
(二)要点:前提是
个图形,且这个图形满足两个条件:
(1)存在直线(对称轴);
(2)沿着这条直线折叠,折痕两旁的部分能
.
(三)注意:一个轴对称图形的对称轴是
且不一定只有一条,可能有两条或多条.
如图所示:
知识点二:轴对称及对称点
(一)轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个
重合,那么就说这两个图形关于这条直线
(或说这两个图形成轴对称),这条直线叫做
.折叠后重合的点是
,也叫做对称点.
(二)要点:
(1)前提是
个图形;
(2)存在一条直线;
(3)两个图形沿着这条直线对折能够完全重合.
(三)注意:
(1)成轴对称的两个图形一定全等;
(2)它与轴对称图形的区别主要是:它是指
个图形,而轴对称图形前提是
个图形;
(3)成轴对称的两个图形除了全等外还有特定的位置关系.如图所示:
知识点三:轴对称与轴对称图形
(一)相互转化:
轴对称图形和轴对称的关系非常密切,若把成轴对称的两个图形看作一个整体,则这个整体就是
;反过来,若把轴对称图形的对称轴两旁的部分看作两个图形,则这两个图形关于这条直线(原对称轴)
.
(二)轴对称、轴对称图形的性质
(1)性质1:若两个图形关于某直线对称,那么对称轴是
;
注:经过线段
并且
于这条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线.
性质1的证明如下:
如图所示,△ABC与△关于l对称,其中点A、是对称点,设交对称轴于点P.将△ABC和△沿l折叠后,点A与重合,则有,∠1=∠2=90°,即对称轴把垂直平分,同样也能把、都垂直平分,于是得出性质1.
(2)性质2:轴对称图形的对称轴也是
.
证明类似性质1.
(3)小结:不论性质1,还是性质2所指的都是只要两个点关于某直线对称,那么这条直线(对称轴)就是这两个点连线的
.也就是说这两条性质所体现的是
与
的关系.也揭示了轴对称(轴对称图形)的实质.
知识点四:线段的垂直平分线
(一)性质1:线段垂直平分线上的点到线段两端点的距离
;
证法一:如图所示,l是线段AB的垂直平分线,P为l上任意一点.如果把AB沿着l对折,A点和B点一定重合,同时PA、PB也应该重合,如果在l上再取一点,连、,则、也应该重合,即它们分别对应相等,由此得出性质1.
证法二:另外,我们还可以从全等的角度得出性质1,过程如下:如上图,
∵
l垂直平分AB,
∴
AO=BO,∠1=∠2.
又∵
PO=PO(公共边),
∴
Rt△PAO≌
(SAS)
∴
PA=PB.
即性质1成立.
(二)性质2:与一条线段两个端点距离相等的点在这条线段的
.
性质2的探究如下:如图所示,作直线PC⊥AB于C,则在Rt△PAC和Rt△PBC中,
PA=PB,PC=PC,
∴
Rt△PAC≌__________,
∴
AC=_______.
即PC垂直平分AB,
所以点P在线段AB垂直平分线上.
(三)小结:
(1)从以上的两个结论可以看出,在线段AB垂直平分线上的点与A、B两点的距离
;反过来与点A、B距离相等的点都在
.综合以上两点可以得出:线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.
(2)线段垂直平分线的两个性质具有不同的作用,性质l是线段的垂直、平分线的性质,可用它来证明线段
的问题;而性质2实质是
的判定.
知识点五:对称轴的作法
(一)若两个图形成轴对称,其对称轴就是任何一对对应点所连线段的
.
因此只要找到一对对应点,再作出连接它们的线段的
就可以得到这两个图形的对称轴.轴对称图形的对称轴作法相同.
(二)例如:A、B两点关于某直线对称,连接AB,作线段AB的垂直平分线就是A、B两点的对称轴,作法如下:
(1)分别以点
为圆心,以大于
的长为半径作弧(若两弧
半径小于或等于AB,则两弧没有交点或切于一点),两弧交于C、D两点;
(2)连
,得直线
,直线CD即为所求.如下图所示:
(三)说明:作对称轴的方法也就是作_________________的方法.用此方法可确定线段的中点,即把线段平分.
知识点六:轴对称变换
(一)由一个平面图形得到它关于某直线的对称图形,这一过程叫
.
(二)注意:
(1)将一个图形进行轴对称变换(作一个图形关于某直线的对称图形).关键是作某些点(关键点)关于这条直线的
.
①如:作点A关于直线l的对称点.
先作AO⊥______于O;再延长AO至使,
则就是A关于l的对称点,如下图所示:
②主要有两步:第一步,过已知点作对称轴的
,得到一个垂线段;第二步,将这个垂线段延长
所到达的点就是已知点关于这条直线(对称轴)的对称点.
(2)成轴对称的两个图形中的任何一个都可以看作是另一个图形经过轴对称变换得到的.同样,一个轴对称图形也可以看作是以它的一部分为基础,经轴对称变换扩展而成的.
(3)经过轴对称变换并结合平移变换我们可得到一些美丽的图案,如图所示:
知识点七:用坐标表示轴对称
(一)关于x轴对称的两个点的横(纵)坐标的关系
已知P点坐标,则它关于x轴的对称点的坐标为
,如下图所示:
即关于x轴的对称的两点,坐标的关系是:横坐标
,纵坐标互为
.
(二)关于y轴对称的两个点横(纵)坐标的关系
已知P点坐标为,则它关于y轴对称点的坐标为
,如上图所示.
即关于y轴对称的两点坐标关系是:纵坐标
,横坐标互为
.
注意:由此我们可以在平面直角坐标系中作出与一个已知图形关于x轴或y轴对称的图形.
(三)关于与x轴(y轴)平行的直线对称的两个点横(纵)坐标的关系
(1)P点坐标关于直线的对称点的坐标为
.
证明:如下图所示,令坐标为,由题意可知,即,故.所以.
同样可以推导出下面的结论.
(2)P点关于直线的对称点的坐标为
,如上图所示.
(
经典例题-自主学习
认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
.
无星号题目要求同学们必须掌握,为基础题型,一个星号的题目综合性稍强
.
)
类型一:对称轴问题
例1.观察下图中的图案,问这些轴对称图形,各有几条对称轴?
思路点拨:对于一个图形的对称轴一定要按定义全方位地去找或按照定义实际操作一下,否则就容易造成漏解或找不到对称轴.
解:
总结升华:
.
举一反三:
【变式1】试说出下列图形的对称轴的条数.
(1)线段;
(2)角;
(3)平行线(两条).
解析:
类型二:轴对称图形的作法
例2.已知△ABC,直线l.求作,使和△ABC关于l对称.
思路点拨:作一个图形关于已知直线的对称图形关键是作出一些特殊点关于已知直线的对称点,所谓的特殊点,即可以决定图形的大小和形状的点,一般来说一个多边形的特殊点就是它的各个
.
作法:
总结升华:
.
举一反三:
【变式】把图中的图形补成以l为对称轴的轴对称图形.
解析:
类型三:中垂线问题
例3.如图所示,在△ABC中,AC=10cm,AB的中垂线交AB于E,交AC于D,
△DBC的周长为16
cm,求BC的长.
思路点拨:欲求BC长,只需求出DB+DC.而DE垂直平分
,故
,此题可解.
解析:
总结升华:
.
举一反三:
【变式1】如图所示,AD垂直平分BC,DE⊥AB,DF⊥AC,垂足分别为E、F.求证DE=DF.
思路点拨:欲证DE=DF,只需证AD是∠BAC的平分线.而AD是BC中垂线可得B、C两点关于
对称,故△ABD和△ACD关于
对称,则可得∠BAD
=
.
证明:
总结升华:
.
【变式2】如图所示,在道路OA、OB的交叉区域内有M、N两所学校,现在要在此区域内建一图书馆P,使它到两条道路距离相等,并且到两所学校距离也相等,求P点位置.
思路点拨:P点到OA、OB距离相等,只需P在
上即可.
P到M、N距离相等,只需P点在
上即可.
解:
总结升华:
.
类型四:最短路问题
☆☆例4.在锐角∠AOB内有一定点P,试在OA、OB上确定两点C、D,使△PCD的周长最短.
思路点拨:△PCD的周长等于PC+CD+PD,要使△PCD的周长最短,根据两点之间线段最短,只需使得PC+CD+PD的大小等于某两点之间的距离,于是考虑作点P关于直线OA和OB的对称点E、F,则△PCD的周长等于线段EF的长.
解析:
总结升华:
.
举一反三:
【变式】草原上两个居民点A、B在河流a的同旁,一汽车从A出发到B,途中需要到河边加水.汽车在哪一点加水,可使行驶的路程最短?在图上画出该点.
思路点拨:若P为直线a上的点,则要使PA+PB最小与线段有关的结论是两点之间
最短,当把PA+PB转化成为一条线段时,点P就是符合条件的点.
解析:
类型五:坐标系中的对称问题
例5.如图,(1)请写出△ABC中各顶点的坐标.(2)在同一坐标系中画出直线m:x=-1,并作出△ABC关于直线m对称的△A′B′C′.(3)若P(a,b)是△ABC中AC边上一点,请表示其在△A′B′C′中对应点的坐标.
思路点拨:直线m:x=-1表示直线m上任意一点的横坐标都等于
,因此过点(-1,0)作_____轴的平行线即直线m.画出直线m后,再作点A、C关于直线m的对称点A′、C′,而点B在直线m上,则其关于直线m对称的点B′就是
.
解析:
总结升华:
.
举一反三:
【变式】如下图,一束光线从y轴上的点A(0,2)出发,经过x轴上点C反射后经过点B(6,6),则光线从点A到点B所经过的路程是(
)
A.10
B.8
C.6
D.
4
答案:
三、总结与测评
要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力.
(
总结规律和方法
——
强化所学
认真回顾总结本部分内容的规律和方法,熟练掌握技能技巧.
)
(一)由一个平面图形得到它的轴对称图形叫做轴对称变换.成轴对称的两个图形中的任何一个可以看着由另一个图形经过_____________后得到.
(二)轴对称变换的性质:
(1)经过轴对称变换得到的图形与原图形的形状、大小完全一样.
(2)经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的
.
(3)连接任意一对对应点的线段被对称轴
.
(三)作一个图形关于某条直线的轴对称图形的步骤:
(1)作出一些关键点或特殊点的对称点.
(2)按原图形的连接方式连接所得到的对称点,即得到原图形的轴对称图形.
(四)点P(x,y)关于x轴对称的点的坐标是
;
点P(x,y)关于y轴对称的点的坐标是
;
点P(x,y)关于原点对称的点的坐标是
.
(五)点P(x,y)关于直线x=m对称的点的坐标是
;
点P(x,y)关于直线y=n对称的点的坐标是
.
14
