人教版 数学 八年级上册12.3角平分线的性质教案
文档属性
| 名称 | 人教版 数学 八年级上册12.3角平分线的性质教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 824.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 00:00:00 | ||
图片预览

文档简介
角平分线的性质
一、目标与策略
明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!
学习目标:
掌握角平分线性质定理及逆定理,并能用定理进行推理论证.
在通过观察——猜想——实践——探究的获取知识的过程中,培养逻辑思维能力、分析问题和解决问题的能力.
通过图形变换及证明题的推理论证,渗透事物间相互转化的思想,培生严谨的学习态度.
重点难点:
重点:角平分线性质定理及逆定理的应用.
难点:熟悉图形变换,能将复杂图形分解成简单的基本图形.
学习策略:
通过探究、交流、练习,掌握并能灵活运用角平分线的性质与判定.
二、学习与应用
(
“凡事预则立,不预则废”
.
科学地预习才能使我们上课听讲更有目的性和针对性
.
我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记
.
)
(
知识回顾
——
复习
学习新知识之前,看看你的知识贮备过关了吗?
)
(一)三角形一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做这个角的
;
(二)能够完全重合的两个三角形叫做
;
(三)全等三角形的对应角
,对应边
;
(四)证明两个三角形全等的条件:
,
,
,
;对于直角三角形还有
.
(
知识要点——预习和课堂学习
认真阅读、理解教材,尝试把下列知识要点内容补充完整,带着自己预习的疑惑认真听课学习.请在虚线部分填写预习内容,在实线部分填写课堂学习内容.课堂笔记或者其它补充填在右栏.
)
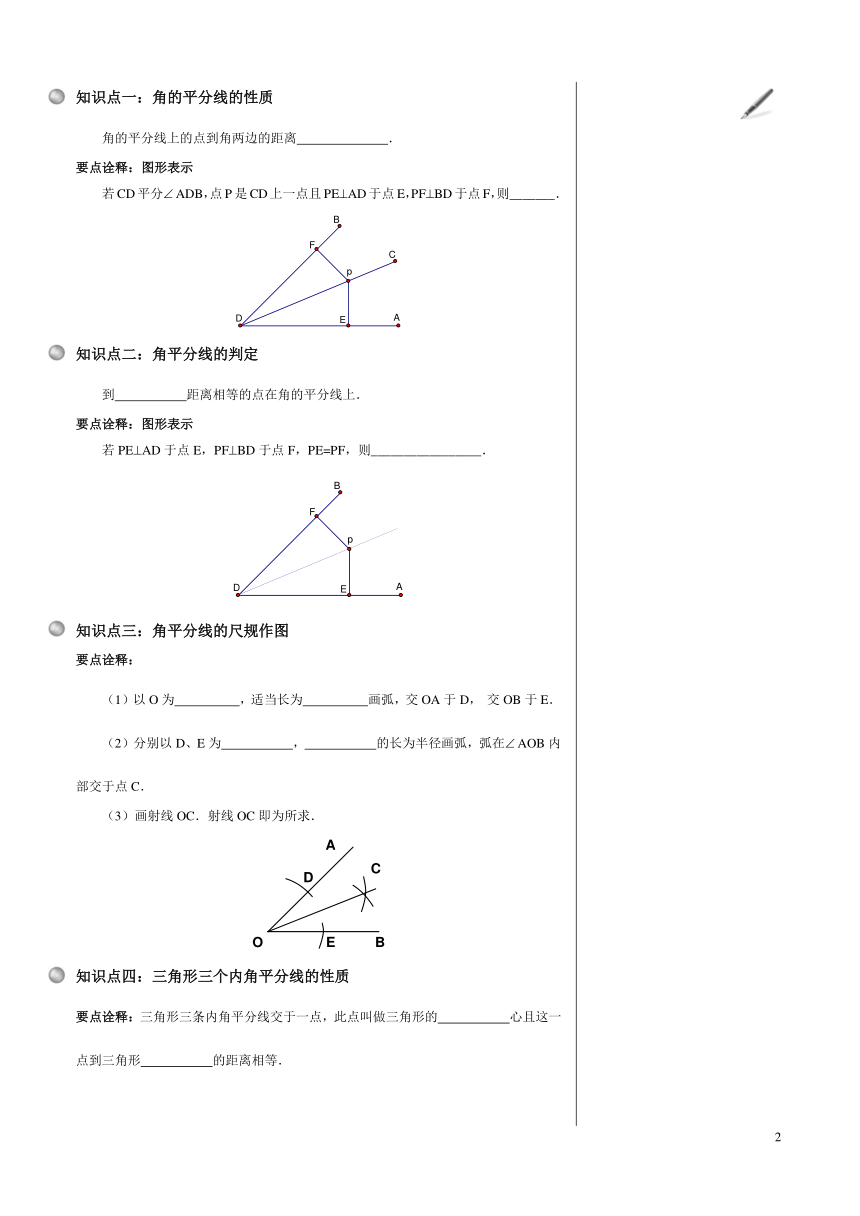
知识点一:角的平分线的性质
角的平分线上的点到角两边的距离
.
要点诠释:图形表示
若CD平分
ADB,点P是CD上一点且PEAD于点E,PFBD于点F,则_______.
知识点二:角平分线的判定
到
距离相等的点在角的平分线上.
要点诠释:图形表示
若PEAD于点E,PFBD于点F,PE=PF,则_________________.
知识点三:角平分线的尺规作图
要点诠释:
(1)以O为
,适当长为
画弧,交OA于D,
交OB于E.
(2)分别以D、E为
,
的长为半径画弧,弧在
AOB内部交于点C.
(3)画射线OC.射线OC即为所求.
知识点四:三角形三个内角平分线的性质
要点诠释:三角形三条内角平分线交于一点,此点叫做三角形的
心且这一点到三角形
的距离相等.
(
经典例题-自主学习
认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
.若有其它补充可填在右栏空白处.
)
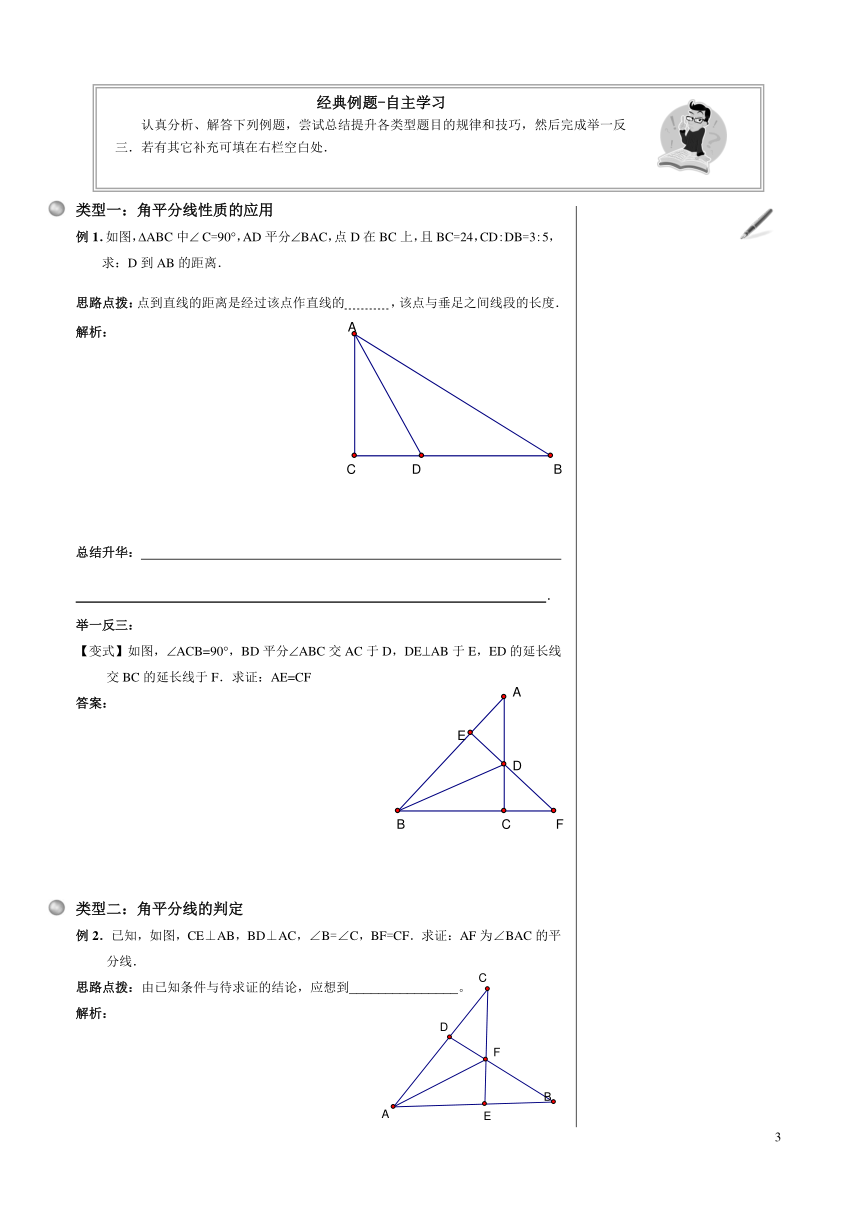
类型一:角平分线性质的应用
例1.如图,ABC中
C=90,AD平分BAC,点D在BC上,且BC=24,CD:DB=3:5,求:D到AB的距离.
思路点拨:点到直线的距离是经过该点作直线的
,该点与垂足之间线段的长度.
解析:
总结升华:
.
举一反三:
【变式】如图,ACB=90,BD平分ABC交AC于D,DEAB于E,ED的延长线交BC的延长线于F.求证:AE=CF
答案:
类型二:角平分线的判定
例2.已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线.
思路点拨:由已知条件与待求证的结论,应想到_______________。
解析:
总结升华:
.
举一反三:
【变式】如图,已知AB=AC,AD=AE,DB与CE相交于O
(1)若DBAC,CEAB,D,E为垂足,试判断点O的位置及OE与OD的大小关系,并证明你的结论.
(2)若D,E不是垂足,是否有同样的结论?并证明你的结论.
答案:
类型三、角平分线的综合应用
☆☆例3.已知:BE是ABC的平分线,AD⊥BE,
求证:BAD=DAC+C
思路点拨:证明一个角等于另外两个角的和的问题,一般有两种途径:
(1)将两个角转化为一个角,再证
.
(2)在和角中做一个角,使它与这两个角中的一个相等,再证余下的部分等于
.
解析:
总结升华:
.
举一反三:
☆☆【变式】在四边形ABCD中,BC>BA,AD=CD,BD平分ABC,
求证:A+C=180°
答案:
三、总结与测评
要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力.
(
总结规律和方法
——
强化所学
认真回顾总结本部分内容的规律和方法,熟练掌握技能技巧.
)
(一)角的平分线是
线,三角形的角平分线是
.
(二)证明线段相等的方法:
(1)
;
(2)
.
(三)证明角相等的方法:
(1)
;
(2)
.
6
一、目标与策略
明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!
学习目标:
掌握角平分线性质定理及逆定理,并能用定理进行推理论证.
在通过观察——猜想——实践——探究的获取知识的过程中,培养逻辑思维能力、分析问题和解决问题的能力.
通过图形变换及证明题的推理论证,渗透事物间相互转化的思想,培生严谨的学习态度.
重点难点:
重点:角平分线性质定理及逆定理的应用.
难点:熟悉图形变换,能将复杂图形分解成简单的基本图形.
学习策略:
通过探究、交流、练习,掌握并能灵活运用角平分线的性质与判定.
二、学习与应用
(
“凡事预则立,不预则废”
.
科学地预习才能使我们上课听讲更有目的性和针对性
.
我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记
.
)
(
知识回顾
——
复习
学习新知识之前,看看你的知识贮备过关了吗?
)
(一)三角形一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做这个角的
;
(二)能够完全重合的两个三角形叫做
;
(三)全等三角形的对应角
,对应边
;
(四)证明两个三角形全等的条件:
,
,
,
;对于直角三角形还有
.
(
知识要点——预习和课堂学习
认真阅读、理解教材,尝试把下列知识要点内容补充完整,带着自己预习的疑惑认真听课学习.请在虚线部分填写预习内容,在实线部分填写课堂学习内容.课堂笔记或者其它补充填在右栏.
)
知识点一:角的平分线的性质
角的平分线上的点到角两边的距离
.
要点诠释:图形表示
若CD平分
ADB,点P是CD上一点且PEAD于点E,PFBD于点F,则_______.
知识点二:角平分线的判定
到
距离相等的点在角的平分线上.
要点诠释:图形表示
若PEAD于点E,PFBD于点F,PE=PF,则_________________.
知识点三:角平分线的尺规作图
要点诠释:
(1)以O为
,适当长为
画弧,交OA于D,
交OB于E.
(2)分别以D、E为
,
的长为半径画弧,弧在
AOB内部交于点C.
(3)画射线OC.射线OC即为所求.
知识点四:三角形三个内角平分线的性质
要点诠释:三角形三条内角平分线交于一点,此点叫做三角形的
心且这一点到三角形
的距离相等.
(
经典例题-自主学习
认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
.若有其它补充可填在右栏空白处.
)
类型一:角平分线性质的应用
例1.如图,ABC中
C=90,AD平分BAC,点D在BC上,且BC=24,CD:DB=3:5,求:D到AB的距离.
思路点拨:点到直线的距离是经过该点作直线的
,该点与垂足之间线段的长度.
解析:
总结升华:
.
举一反三:
【变式】如图,ACB=90,BD平分ABC交AC于D,DEAB于E,ED的延长线交BC的延长线于F.求证:AE=CF
答案:
类型二:角平分线的判定
例2.已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线.
思路点拨:由已知条件与待求证的结论,应想到_______________。
解析:
总结升华:
.
举一反三:
【变式】如图,已知AB=AC,AD=AE,DB与CE相交于O
(1)若DBAC,CEAB,D,E为垂足,试判断点O的位置及OE与OD的大小关系,并证明你的结论.
(2)若D,E不是垂足,是否有同样的结论?并证明你的结论.
答案:
类型三、角平分线的综合应用
☆☆例3.已知:BE是ABC的平分线,AD⊥BE,
求证:BAD=DAC+C
思路点拨:证明一个角等于另外两个角的和的问题,一般有两种途径:
(1)将两个角转化为一个角,再证
.
(2)在和角中做一个角,使它与这两个角中的一个相等,再证余下的部分等于
.
解析:
总结升华:
.
举一反三:
☆☆【变式】在四边形ABCD中,BC>BA,AD=CD,BD平分ABC,
求证:A+C=180°
答案:
三、总结与测评
要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力.
(
总结规律和方法
——
强化所学
认真回顾总结本部分内容的规律和方法,熟练掌握技能技巧.
)
(一)角的平分线是
线,三角形的角平分线是
.
(二)证明线段相等的方法:
(1)
;
(2)
.
(三)证明角相等的方法:
(1)
;
(2)
.
6
