沪科版八年级全册 物理 课件 第十章 机械与人 复习课件(41张)
文档属性
| 名称 | 沪科版八年级全册 物理 课件 第十章 机械与人 复习课件(41张) |  | |
| 格式 | pptx | ||
| 文件大小 | 400.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-21 17:02:40 | ||
图片预览









文档简介
第十章 机械与人 复习课件
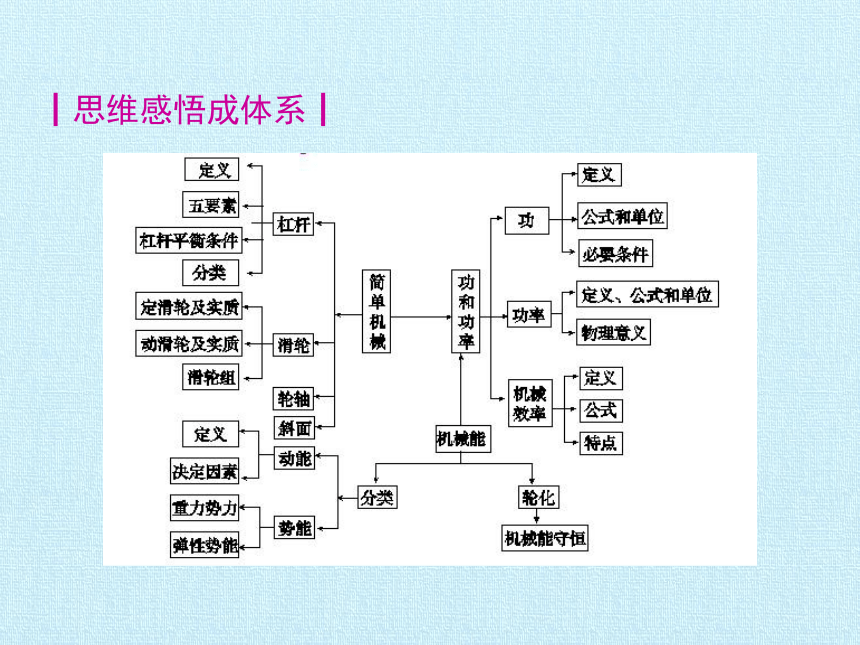
┃思维感悟成体系┃
┃回眸教材析知识┃
1.杠杆
直接搬动很重的大石头很困难,利用撬棒就可以较容易办到,在力的作用下,撬棒就是能绕着一个固定点转动的硬棒,叫 。撬棒属于省力杠杆,但是费了 ;用筷子夹食物,筷子就是一种费力杠杆,只要手指稍微一动 , 筷子就可以夹很多东西,虽然费了 ,但省了 ,使操作更加方便。
杠杆
距离
距离
力
2.滑轮和滑轮组
观察人们生活中利用简单机械的情景,有时人们利用动滑轮,目的是省 ,但费了 ;有时利用定滑轮,不省力,但改变了 ,使操作更为方便。要想即省力又改变力的方向, 就可以将两者组合,组成 ,起重机上的滑轮组合就是实例之一。
力
距离
滑轮组
力的方向
3.功的必要因素
某同学踢足球,球离开脚后飞出10m远,足球飞出10m的过程中人不做功。物理学中规定:功等于
的乘积。功包括两个必要因素:①作用在物体上的 ;②物体在 的方向上通过的距离。不做功的三种情况:有力无距离,例如提重物却没有提起;有距离无力,弹珠在水平桌面上被弹出继续前进,但人没有做功;力和距离垂直,例如物体在水平冰面上匀速滑行,水平方向没有力做功,此时虽然有重力作用在物体上,但重力方向与物体运动方向垂直没有做功。
力跟物体在力
的方向上通过的距离
力
力
4.功的原理
事实告诉我们,使用扳手拧螺丝要省力必须费 ,钓鱼时要省距离必须费 ,既 的机械是没有的。使用机械时,人们所做的功,都不会少于直接用手所做的功,即: 。
使用机械虽然不能省功,但人类仍然使用,是因为使用机械或者可以 、或者可以 、也可以改变
,给人类工作带来很多方便。
理想机械(忽略摩擦和机械本身的重力):使用机械时,人们所做的功(Fs) 直接用手对重物所做的功(Gh)。
距离
力
省力又省距离
使用任何机械都不省功
等于
力的方向
省距离
省力
5.功率
功率是指机械在 里完成的功, 表示做功 的物理量。例如,某小轿车功率66kW,它表示:小轿车1s内做功66000J。对于功率一定的机械,由公式P=—=Fv可知,当速度越小时,产生的拉力越大,例如:
汽车载重上坡时,要挂低挡来获得较大的拉力。
6.机械效率
(1)机械效率是指有用功跟总功的 。不同机械的机械效率表达式及其特点:
单位时间
快慢
比值
t
W
公式:η=———
斜面:η=——
定滑轮:η=——=——=—
动滑轮:η=——=——=——
滑轮组:η=——=——=——
(2)提高机械效率的方法:减小机械自重、减小机件间的摩擦。
W有用
W总
Gh
FL
Gh
Fs
Gh
Fh
G
F
Gh
Gh
Fs
F2h
2F
G
G
nF
Fnh
Gh
Gh
Fs
7.机械能及其转化
荡秋千人处于最高点时,由于人被举高而具有 能;下降过程中,高度减小,重力势能 ,速度逐渐增大,动能 ,即人的重力势能向动能转化;到达最低点,人的速度最大,动能最大,高度最小,重力势能最小;继续向最高点上升过程中, 又转化为 ;再次到达最高点时,动能减小到零,转化的重力势能最大。转化过程中,若没有能量损失,机械能的总量不变,即两者之和不变,这就是机械能守恒。
动能不仅与速度有关,还与物体的质量有关,速度相同时,质量越大,动能越 ,同速行驶的火车动能大于汽车的动能;重力势能不仅与高度有关,还与物体的质量有关,高度相同时,质量越大,重力势能也越 ,高度相同的铁钉和铁锤,铁钉重力势能要 铁锤的重力势能。
重力势
减小
增大
动能
小于
大
大
重力势能
典例1:杠杆平衡条件的探究和应用
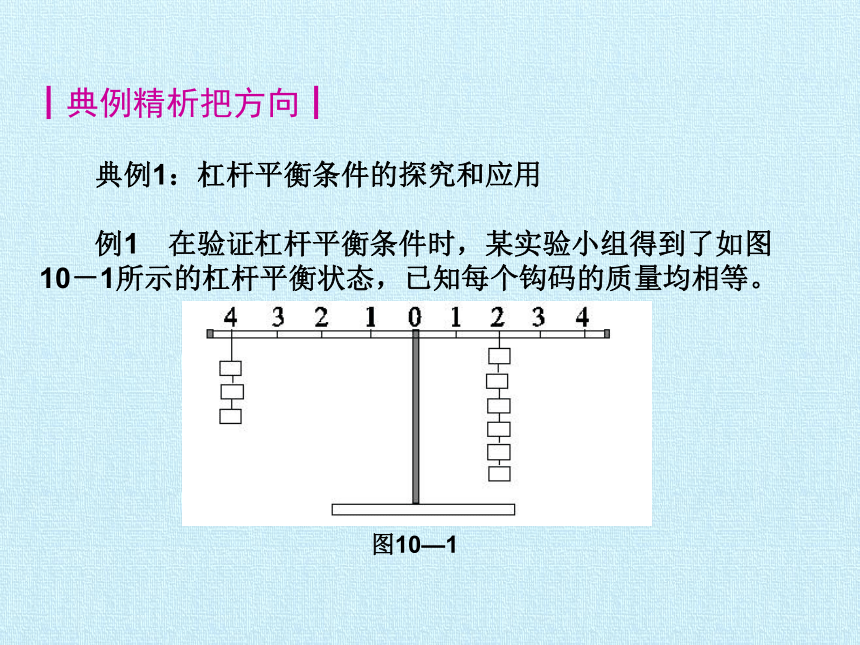
例1 在验证杠杆平衡条件时,某实验小组得到了如图10-1所示的杠杆平衡状态,已知每个钩码的质量均相等。
┃典例精析把方向┃
图10—1
(1)若钩码所挂位置不动,将左边的钩码去掉一个,为使杠杆仍然保持平衡,右边的钩码该拿掉 个。
(2)杠杆的平衡条件为 。
2
动力×动力臂=阻力×阻力臂
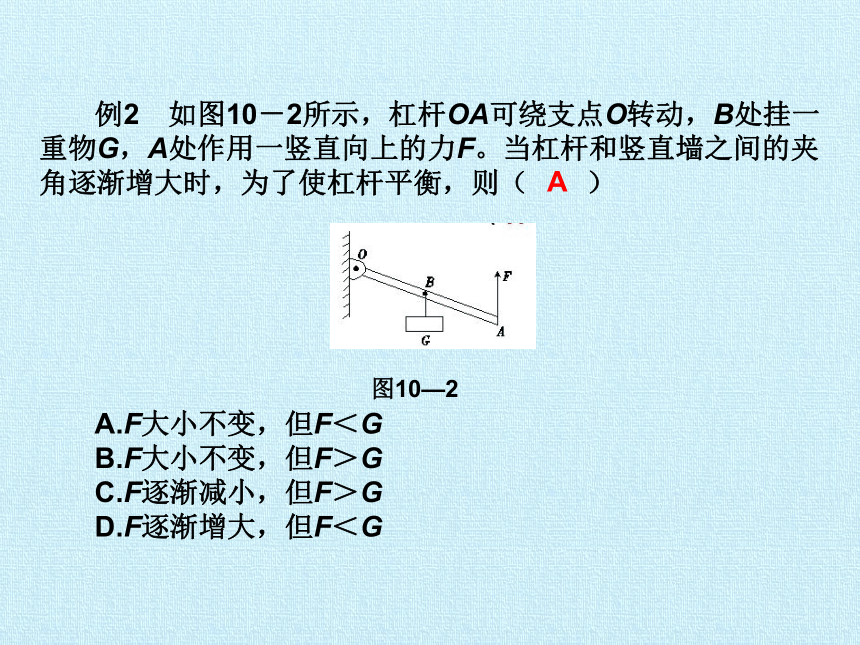
例2 如图10-2所示,杠杆OA可绕支点O转动,B处挂一重物G,A处作用一竖直向上的力F。当杠杆和竖直墙之间的夹角逐渐增大时,为了使杠杆平衡,则( )
A.F大小不变,但F<G
B.F大小不变,但F>G
C.F逐渐减小,但F>G
D.F逐渐增大,但F<G
A
图10—2
[解析]当杠杆和竖直墙之间夹角逐渐增大时,由于动力
是竖直向上的,所以动力臂和阻力臂的比值是不变的,由杠
杆平衡条件——=——可知,力的大小不变。
方法点拨:
本题属于动态平衡问题,解决此类问题的关键在于找到不变量和动态量。根据杠杆平衡条件F1L1=F1L2,代入不变量,进而判断动态量的变化情况。
F1
F2
L2
L1
典例2:滑轮组的应用与设计
例3 请在图10-3中画出用滑轮组提升重物,拉力F=的绳子的绕法。(不计动滑轮重、绳重和摩擦)
[答案] 如图所示
图10—3
方法点拨:
关于滑轮组提升(或水平拉)物体时,承担重物绳子的
股数的判断和根据题目的具体要求设计滑轮组的组装的解题
步骤:①根据公式n= ,求出绳子的股数;②利
用“奇动偶定”原则解决相关问题。
G物+G动
F
典例3:功的计算
例4 如图10-4所示,用水平力F拉着重为100N的物体,在水平地面上向右匀速移动了5m,物体所受地面的摩擦力大小为20N,则( )
A.重力做的功是500J
B.拉力大小为100N
C.拉力大小为120N
D.拉力做的功为100J
D
图10—4
方法点拨:
计算功的大小时,要特别注意:力与距离二者要在同一个方向上。还要注意通过物体的平衡条件判断物体的受力情况,求力的大小。
典例4:功率的测量
例5 如图10-5所示,粗略测量小明同学引体向上运动的功率时,下列物理量不需要测量的是( )
A.小明的质量
B.单杠的高度
C.每次身体上升的高度
D.做引体向上的时间
B
图10—5
方法点拨:
测量功率的大小的思路:根据功率的计算公式P=—
确定所需测量的物理量,测量功率需要得到功和对应做功
所需要的时间,测量功时注意力和距离的对应。
W
t
典例5:机械效率的探究
例6 用如图10-6所示的实验装置测量杠杆的机械效率。实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。
图10—6
(1)实验中,将杠杆拉至图中虚线位置,测力计的示数F为 N,钩码总重G为1.0N,钩码上升高度h为0.1m,测力计移动距离s为0.3m,则杠杆的机械效率为 %。请写出使用该杠杆做额外功的一个原因:
。
(2)为了进一步研究杠杆的机械效率与哪些因素有关,一位同学用该实验装置,先后将钩码挂在A、B两点,测量并计算得到下表所示的两组数据。
实验
次数
钩码悬
挂点
钩码总
重G/N
钩码移
动距离
h/m
拉力
F/N
测力计
移动距
离s/m
机械效
率η/%
1
A点
1.5
0.10
0.7
0.30
71.4
2
B点
2.0
0.15
1.2
0.30
83.3
0.5
66.7
使用杠杆时需要克
服杠杆自重(克服摩擦力)等做功
根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”的结论?答: ;请简要说明两条理由:① ;② 。
方法点评:
杠杆的机械效率:杠杆的支点改变,悬挂点的改变都会使额外功的大小改变,即克服杠杆自重所做的功改变。
不能
两次实验时钩码没有挂在同一位置
仅根据一次对比实验所得结论是不可靠的
典例6:机械能的转化
例7 同学们都玩过秋千吧,闭上眼睛,那种时高时低的感觉如同在飞……你知道其中能量的转化吗?图10-7是小孩荡秋千的示意图,下列分析正确的是( )
C
图10—7
A.小孩在A点具有最大动能
B.小孩从C荡到B的过程中,动能转化为势能
C.小孩从B荡到C的过程中,动能转化为势能
D.小孩从A荡到B的过程中,在B点的机械能大于A点的机械能
方法点拨:
判断动能、势能的转化时,首先看变化前的物体所具有的能的状态,再看变化后物体所具有的能的状态,前后比较就可以判断哪种能发生了变化,由何种能转化为何种能。
1.如图10-8所示是安置在小区门口的栏杆的示意图,当在A处施加一个动力时,可将栏杆拉起来,它是一根( )
A.省力杠杆 B.费力杠杆
C.等臂杠杆 D.无法确定
┃实战演习成高手┃
B
图10—8
[解析]当在A处施加一个动力时,左侧立柱是支点,杆的重心在杆的中间,则阻力臂约为杆长的一半,而动力臂只是A点到支点的距离,所以动力臂远远小于阻力臂,属于费力杠杆。
2.将一个省力的机械和一个省距离的机械组装成一个组合机械,当利用这个组合机械做功时( )
A.一定不能省功
B.一定可以省力
C.一定可以省距离
D.一定能省功
A
3.如图10-9所示的四种情景中,人对物体做功的是( )
B
图10—9
[解析]A、C、D选项中有力没有距离,所以不做功。
4.中考体育跳绳项目测试中,小明同学在1min内跳了120次,则他跳绳时的功率大约是( )
A.0.5W B.5W
C.50W D.500W
[解析]小明体重约500N,每次升高5cm,P=—=
——————————=50W。
C
W
t
500N×0.05m×120
60s
5.如图10-10所示,用F=50N的水平拉力,通过一个动滑轮,使重为200N的物体A水平向右匀速移动了
3m,在这个过程中( )
A.拉力F做了150J的功
B.拉力F做了300J的功
C.重力做了600J的功
D.重力做了1200J的功
B
图10—10
6.如图10-11所示是某跳水运动员正在进行训练的情景,从起跳至落到水面的过程中,运动员的动能与重力势能变化的情况是( )
A.动能一直减小,重力势能一直增大
B.动能一直增大,重力势能一直减小
C.动能先增大后减小,重力势能先减小后增大
D.动能先减小后增大,重力势能先增大后减小
D
图10—11
7.如图10-12所示,若人手拉力F=50N,则货物重
N(不考虑动滑轮和摩擦),A钩所受的拉力为
N,B钩所受的拉力为 N。
100
图10—12
50
100
8.某人在水平地面上用100N的水平推力推动重500N的物体,使物体以0.2m/s的速度匀速移动了3m,地面对物体的摩擦力是 N,此人对物体做的功是
J,功率是 W。
100
300
20
9.如图10-13所示,运动员射箭时用力将弓斜向上拉开,在放开箭的瞬间,弓的 能转化为箭的
能,箭在空中向上飞行的过程中,箭的 能增大。
图10—13
弹性势
重力势
动
10.如图10-14所示,在课桌的C点用最小的力把桌腿B抬离地面,在抬起时桌腿A没有滑动,请在C点画出这个力的示意图,并标出它的力臂L。
图10—14
[答案]如图所示
11.小芳同学设计了一个高度可调节的斜面来探究斜面的省力情况、斜面的机械效率与斜面的倾斜程度之间的关系,如图10-15所示,她首先测出小车重,然后用弹簧测力计沿斜面拉动小车。调节斜面倾角θ的大小,多次测量,得到下表所示的数据:
图10—15
(1)请你替小芳在上表中的空格处填上适当的数据。
斜面倾
斜角θ
小车重
G/N
斜面高
h/m
斜面长
s/m
拉力
F/N
有用功
W有/J
总功
W总/J
机械效
率η
12°
5
0.2
1
2.1
1
2.1
48%
30°
5
0.5
1
3.6
2.5
69%
45°
5
0.7
1
4.3
3.5
4.3
3.6
81%
(2)分析上表中的数据,可以得出的探究结论是:斜面倾斜角θ越大, 。
(3)实验过程中拉力的方向应与斜面 。
(4)若想探究斜面的机械效率与物重的关系,则要保持 不变,斜面的光滑程度不变,只改变
。
机械效率越大
平行(保持一致)
斜面倾斜角θ
小车重
12.江西省三清山是我国著名的道教圣地和旅游景点。三清山索道全长2426m,上、下高度差约600m,单个吊车载满两人后的总重是2500N。以单个吊车载满两人为
例,试回答下列问题。
图10—16
(1)吊车与索道的接触面积以0.01m2计,索道上挂吊车处的钢索承受的压强是多大?
(2)单个吊车从索道最高处运行到最低处,吊车和人的重力做多少功?
(3)若单个吊车从索道最高处运行到最低处,用时
20min,吊车和人的重力做功的功率是多少?
[答案](1)2.5×105Pa (2)1.5×106J (3)1250W
[解析](1)p=—=————=2.5×105Pa;
(2)W=Gh=2500N×600m=1.5×106J;
(3)P=—— =—————=1250W。
F
S
2500N
0.01m2
W
t
1.5×106J
1200s
谢 谢
┃思维感悟成体系┃
┃回眸教材析知识┃
1.杠杆
直接搬动很重的大石头很困难,利用撬棒就可以较容易办到,在力的作用下,撬棒就是能绕着一个固定点转动的硬棒,叫 。撬棒属于省力杠杆,但是费了 ;用筷子夹食物,筷子就是一种费力杠杆,只要手指稍微一动 , 筷子就可以夹很多东西,虽然费了 ,但省了 ,使操作更加方便。
杠杆
距离
距离
力
2.滑轮和滑轮组
观察人们生活中利用简单机械的情景,有时人们利用动滑轮,目的是省 ,但费了 ;有时利用定滑轮,不省力,但改变了 ,使操作更为方便。要想即省力又改变力的方向, 就可以将两者组合,组成 ,起重机上的滑轮组合就是实例之一。
力
距离
滑轮组
力的方向
3.功的必要因素
某同学踢足球,球离开脚后飞出10m远,足球飞出10m的过程中人不做功。物理学中规定:功等于
的乘积。功包括两个必要因素:①作用在物体上的 ;②物体在 的方向上通过的距离。不做功的三种情况:有力无距离,例如提重物却没有提起;有距离无力,弹珠在水平桌面上被弹出继续前进,但人没有做功;力和距离垂直,例如物体在水平冰面上匀速滑行,水平方向没有力做功,此时虽然有重力作用在物体上,但重力方向与物体运动方向垂直没有做功。
力跟物体在力
的方向上通过的距离
力
力
4.功的原理
事实告诉我们,使用扳手拧螺丝要省力必须费 ,钓鱼时要省距离必须费 ,既 的机械是没有的。使用机械时,人们所做的功,都不会少于直接用手所做的功,即: 。
使用机械虽然不能省功,但人类仍然使用,是因为使用机械或者可以 、或者可以 、也可以改变
,给人类工作带来很多方便。
理想机械(忽略摩擦和机械本身的重力):使用机械时,人们所做的功(Fs) 直接用手对重物所做的功(Gh)。
距离
力
省力又省距离
使用任何机械都不省功
等于
力的方向
省距离
省力
5.功率
功率是指机械在 里完成的功, 表示做功 的物理量。例如,某小轿车功率66kW,它表示:小轿车1s内做功66000J。对于功率一定的机械,由公式P=—=Fv可知,当速度越小时,产生的拉力越大,例如:
汽车载重上坡时,要挂低挡来获得较大的拉力。
6.机械效率
(1)机械效率是指有用功跟总功的 。不同机械的机械效率表达式及其特点:
单位时间
快慢
比值
t
W
公式:η=———
斜面:η=——
定滑轮:η=——=——=—
动滑轮:η=——=——=——
滑轮组:η=——=——=——
(2)提高机械效率的方法:减小机械自重、减小机件间的摩擦。
W有用
W总
Gh
FL
Gh
Fs
Gh
Fh
G
F
Gh
Gh
Fs
F2h
2F
G
G
nF
Fnh
Gh
Gh
Fs
7.机械能及其转化
荡秋千人处于最高点时,由于人被举高而具有 能;下降过程中,高度减小,重力势能 ,速度逐渐增大,动能 ,即人的重力势能向动能转化;到达最低点,人的速度最大,动能最大,高度最小,重力势能最小;继续向最高点上升过程中, 又转化为 ;再次到达最高点时,动能减小到零,转化的重力势能最大。转化过程中,若没有能量损失,机械能的总量不变,即两者之和不变,这就是机械能守恒。
动能不仅与速度有关,还与物体的质量有关,速度相同时,质量越大,动能越 ,同速行驶的火车动能大于汽车的动能;重力势能不仅与高度有关,还与物体的质量有关,高度相同时,质量越大,重力势能也越 ,高度相同的铁钉和铁锤,铁钉重力势能要 铁锤的重力势能。
重力势
减小
增大
动能
小于
大
大
重力势能
典例1:杠杆平衡条件的探究和应用
例1 在验证杠杆平衡条件时,某实验小组得到了如图10-1所示的杠杆平衡状态,已知每个钩码的质量均相等。
┃典例精析把方向┃
图10—1
(1)若钩码所挂位置不动,将左边的钩码去掉一个,为使杠杆仍然保持平衡,右边的钩码该拿掉 个。
(2)杠杆的平衡条件为 。
2
动力×动力臂=阻力×阻力臂
例2 如图10-2所示,杠杆OA可绕支点O转动,B处挂一重物G,A处作用一竖直向上的力F。当杠杆和竖直墙之间的夹角逐渐增大时,为了使杠杆平衡,则( )
A.F大小不变,但F<G
B.F大小不变,但F>G
C.F逐渐减小,但F>G
D.F逐渐增大,但F<G
A
图10—2
[解析]当杠杆和竖直墙之间夹角逐渐增大时,由于动力
是竖直向上的,所以动力臂和阻力臂的比值是不变的,由杠
杆平衡条件——=——可知,力的大小不变。
方法点拨:
本题属于动态平衡问题,解决此类问题的关键在于找到不变量和动态量。根据杠杆平衡条件F1L1=F1L2,代入不变量,进而判断动态量的变化情况。
F1
F2
L2
L1
典例2:滑轮组的应用与设计
例3 请在图10-3中画出用滑轮组提升重物,拉力F=的绳子的绕法。(不计动滑轮重、绳重和摩擦)
[答案] 如图所示
图10—3
方法点拨:
关于滑轮组提升(或水平拉)物体时,承担重物绳子的
股数的判断和根据题目的具体要求设计滑轮组的组装的解题
步骤:①根据公式n= ,求出绳子的股数;②利
用“奇动偶定”原则解决相关问题。
G物+G动
F
典例3:功的计算
例4 如图10-4所示,用水平力F拉着重为100N的物体,在水平地面上向右匀速移动了5m,物体所受地面的摩擦力大小为20N,则( )
A.重力做的功是500J
B.拉力大小为100N
C.拉力大小为120N
D.拉力做的功为100J
D
图10—4
方法点拨:
计算功的大小时,要特别注意:力与距离二者要在同一个方向上。还要注意通过物体的平衡条件判断物体的受力情况,求力的大小。
典例4:功率的测量
例5 如图10-5所示,粗略测量小明同学引体向上运动的功率时,下列物理量不需要测量的是( )
A.小明的质量
B.单杠的高度
C.每次身体上升的高度
D.做引体向上的时间
B
图10—5
方法点拨:
测量功率的大小的思路:根据功率的计算公式P=—
确定所需测量的物理量,测量功率需要得到功和对应做功
所需要的时间,测量功时注意力和距离的对应。
W
t
典例5:机械效率的探究
例6 用如图10-6所示的实验装置测量杠杆的机械效率。实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。
图10—6
(1)实验中,将杠杆拉至图中虚线位置,测力计的示数F为 N,钩码总重G为1.0N,钩码上升高度h为0.1m,测力计移动距离s为0.3m,则杠杆的机械效率为 %。请写出使用该杠杆做额外功的一个原因:
。
(2)为了进一步研究杠杆的机械效率与哪些因素有关,一位同学用该实验装置,先后将钩码挂在A、B两点,测量并计算得到下表所示的两组数据。
实验
次数
钩码悬
挂点
钩码总
重G/N
钩码移
动距离
h/m
拉力
F/N
测力计
移动距
离s/m
机械效
率η/%
1
A点
1.5
0.10
0.7
0.30
71.4
2
B点
2.0
0.15
1.2
0.30
83.3
0.5
66.7
使用杠杆时需要克
服杠杆自重(克服摩擦力)等做功
根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”的结论?答: ;请简要说明两条理由:① ;② 。
方法点评:
杠杆的机械效率:杠杆的支点改变,悬挂点的改变都会使额外功的大小改变,即克服杠杆自重所做的功改变。
不能
两次实验时钩码没有挂在同一位置
仅根据一次对比实验所得结论是不可靠的
典例6:机械能的转化
例7 同学们都玩过秋千吧,闭上眼睛,那种时高时低的感觉如同在飞……你知道其中能量的转化吗?图10-7是小孩荡秋千的示意图,下列分析正确的是( )
C
图10—7
A.小孩在A点具有最大动能
B.小孩从C荡到B的过程中,动能转化为势能
C.小孩从B荡到C的过程中,动能转化为势能
D.小孩从A荡到B的过程中,在B点的机械能大于A点的机械能
方法点拨:
判断动能、势能的转化时,首先看变化前的物体所具有的能的状态,再看变化后物体所具有的能的状态,前后比较就可以判断哪种能发生了变化,由何种能转化为何种能。
1.如图10-8所示是安置在小区门口的栏杆的示意图,当在A处施加一个动力时,可将栏杆拉起来,它是一根( )
A.省力杠杆 B.费力杠杆
C.等臂杠杆 D.无法确定
┃实战演习成高手┃
B
图10—8
[解析]当在A处施加一个动力时,左侧立柱是支点,杆的重心在杆的中间,则阻力臂约为杆长的一半,而动力臂只是A点到支点的距离,所以动力臂远远小于阻力臂,属于费力杠杆。
2.将一个省力的机械和一个省距离的机械组装成一个组合机械,当利用这个组合机械做功时( )
A.一定不能省功
B.一定可以省力
C.一定可以省距离
D.一定能省功
A
3.如图10-9所示的四种情景中,人对物体做功的是( )
B
图10—9
[解析]A、C、D选项中有力没有距离,所以不做功。
4.中考体育跳绳项目测试中,小明同学在1min内跳了120次,则他跳绳时的功率大约是( )
A.0.5W B.5W
C.50W D.500W
[解析]小明体重约500N,每次升高5cm,P=—=
——————————=50W。
C
W
t
500N×0.05m×120
60s
5.如图10-10所示,用F=50N的水平拉力,通过一个动滑轮,使重为200N的物体A水平向右匀速移动了
3m,在这个过程中( )
A.拉力F做了150J的功
B.拉力F做了300J的功
C.重力做了600J的功
D.重力做了1200J的功
B
图10—10
6.如图10-11所示是某跳水运动员正在进行训练的情景,从起跳至落到水面的过程中,运动员的动能与重力势能变化的情况是( )
A.动能一直减小,重力势能一直增大
B.动能一直增大,重力势能一直减小
C.动能先增大后减小,重力势能先减小后增大
D.动能先减小后增大,重力势能先增大后减小
D
图10—11
7.如图10-12所示,若人手拉力F=50N,则货物重
N(不考虑动滑轮和摩擦),A钩所受的拉力为
N,B钩所受的拉力为 N。
100
图10—12
50
100
8.某人在水平地面上用100N的水平推力推动重500N的物体,使物体以0.2m/s的速度匀速移动了3m,地面对物体的摩擦力是 N,此人对物体做的功是
J,功率是 W。
100
300
20
9.如图10-13所示,运动员射箭时用力将弓斜向上拉开,在放开箭的瞬间,弓的 能转化为箭的
能,箭在空中向上飞行的过程中,箭的 能增大。
图10—13
弹性势
重力势
动
10.如图10-14所示,在课桌的C点用最小的力把桌腿B抬离地面,在抬起时桌腿A没有滑动,请在C点画出这个力的示意图,并标出它的力臂L。
图10—14
[答案]如图所示
11.小芳同学设计了一个高度可调节的斜面来探究斜面的省力情况、斜面的机械效率与斜面的倾斜程度之间的关系,如图10-15所示,她首先测出小车重,然后用弹簧测力计沿斜面拉动小车。调节斜面倾角θ的大小,多次测量,得到下表所示的数据:
图10—15
(1)请你替小芳在上表中的空格处填上适当的数据。
斜面倾
斜角θ
小车重
G/N
斜面高
h/m
斜面长
s/m
拉力
F/N
有用功
W有/J
总功
W总/J
机械效
率η
12°
5
0.2
1
2.1
1
2.1
48%
30°
5
0.5
1
3.6
2.5
69%
45°
5
0.7
1
4.3
3.5
4.3
3.6
81%
(2)分析上表中的数据,可以得出的探究结论是:斜面倾斜角θ越大, 。
(3)实验过程中拉力的方向应与斜面 。
(4)若想探究斜面的机械效率与物重的关系,则要保持 不变,斜面的光滑程度不变,只改变
。
机械效率越大
平行(保持一致)
斜面倾斜角θ
小车重
12.江西省三清山是我国著名的道教圣地和旅游景点。三清山索道全长2426m,上、下高度差约600m,单个吊车载满两人后的总重是2500N。以单个吊车载满两人为
例,试回答下列问题。
图10—16
(1)吊车与索道的接触面积以0.01m2计,索道上挂吊车处的钢索承受的压强是多大?
(2)单个吊车从索道最高处运行到最低处,吊车和人的重力做多少功?
(3)若单个吊车从索道最高处运行到最低处,用时
20min,吊车和人的重力做功的功率是多少?
[答案](1)2.5×105Pa (2)1.5×106J (3)1250W
[解析](1)p=—=————=2.5×105Pa;
(2)W=Gh=2500N×600m=1.5×106J;
(3)P=—— =—————=1250W。
F
S
2500N
0.01m2
W
t
1.5×106J
1200s
谢 谢
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
