1.2.4绝对值(2)-人教版七年级数学上册课件(共18张PPT)
文档属性
| 名称 | 1.2.4绝对值(2)-人教版七年级数学上册课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 621.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 08:37:39 | ||
图片预览





文档简介
数学是思维的体操
学习赢得智慧人生
1.2.4 绝对值
第2课时 有理数大小的比较
1.2 有理数
数学是思维的体操
学习赢得智慧人生
教学 重、难点与关键
1.重点:会利用绝对值比较有理数的大小.
2.难点:两个负数的大小比较.
3.关键:正确理解绝对值的概念
数学是思维的体操
学习赢得智慧人生
复习回顾
3.绝对值的概念
4.怎样求一个数的绝对值
5.求2题中各数的绝对值
一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
0的绝对值是0
1.数轴的定义
2.在数轴上表示以下各数
%
1
-3
-2
-1
2
3
0
%
| |
%
=
%
数学是思维的体操
学习赢得智慧人生
在小学我们学过了比较两个数的大小,把数扩充到有理数以后怎样比较两个有理数的大小呢
下图表示元旦当天我国5个城市的最低气温.
武汉4 ℃ 秦皇岛 -12℃ 上海0℃ 深圳14℃ 长春-16℃
思考:
问题:
请把这五个城市的最低气温由低到高排列
数学是思维的体操
学习赢得智慧人生
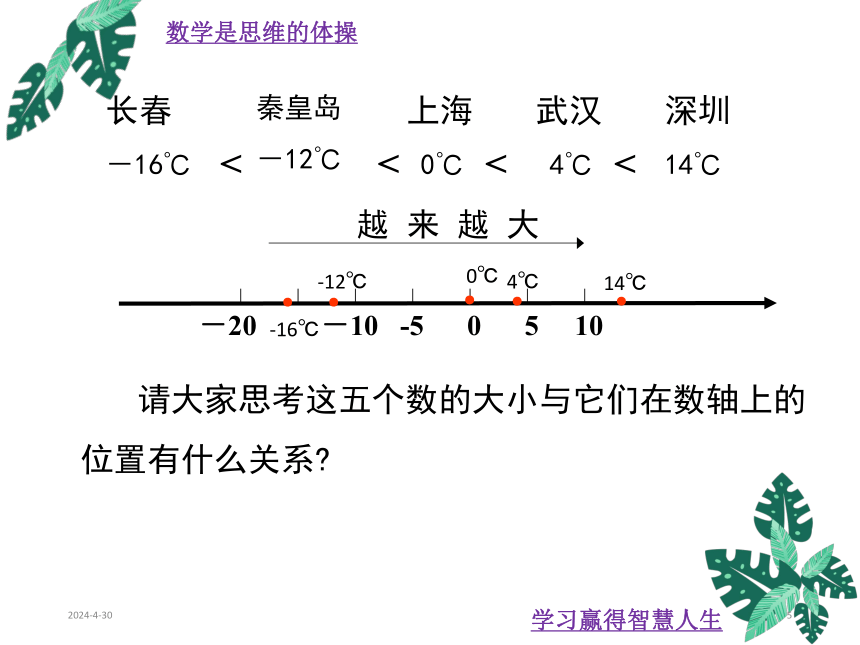
请大家思考这五个数的大小与它们在数轴上的位置有什么关系?
越 来 越 大
长春
-16℃
秦皇岛
-12℃
上海
0℃
武汉
4℃
深圳
14℃
<
<
<
<
-20 -10 -5 0 5 10
●
●
●
●
●
-12℃
-16℃
0℃
4℃
14℃
数学是思维的体操
学习赢得智慧人生
-20 -10 -5 0 5 10
●
●
●
●
●
-12℃
-16℃
0℃
4℃
14℃
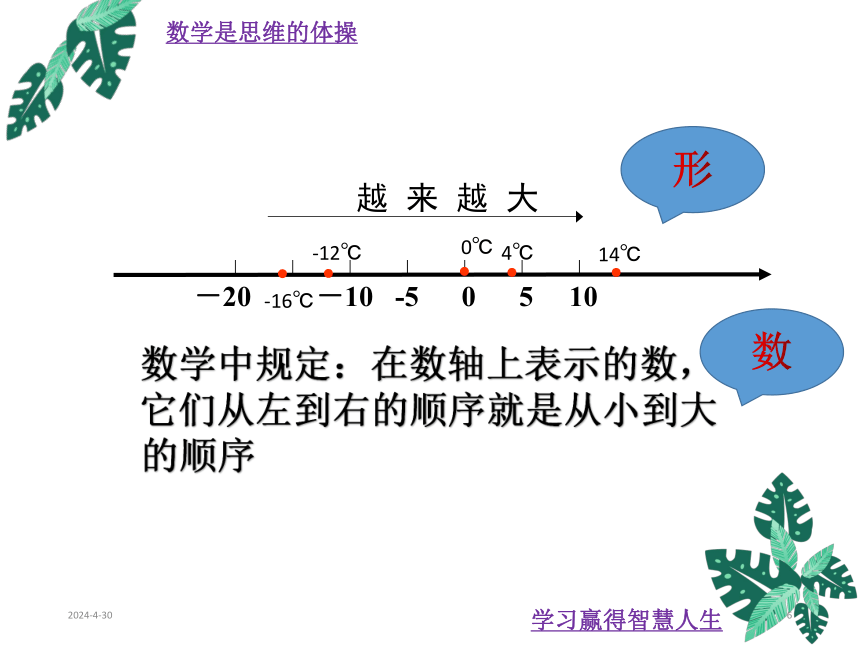
数学中规定:在数轴上表示的数,它们从左到右的顺序就是从小到大的顺序
越 来 越 大
数
形
数学是思维的体操
学习赢得智慧人生
有理数的大小比较的法则
(1)正数大于0,0大于负数,正数大于一切负数
(2)两个负数,绝对值大的反而小
例如:2 0,0 -1,-3 2,-5 -3
<
<
>
>
数学是思维的体操
学习赢得智慧人生
比较两个有理数的大小的方法
1.利用数轴比较
在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
数学是思维的体操
学习赢得智慧人生
比较两个有理数的大小的方法
2.利用绝对值比较两个同号的数
两个负数,绝对值大的反而小
两个正数,绝对值大的这个数也大
归纳
异号两数比较大小,要考虑它们的正负;
同号两数比较大小,要考虑它们的绝对值。
数学是思维的体操
学习赢得智慧人生
%
比较下列各数的大小
%
1
-3
-2
-1
2
3
0
解:方法一利用数轴
方法二利用法则
%
%
数学是思维的体操
学习赢得智慧人生
典例分析
例1:比较下列各对数的大小:
(1)
(2)
(3)
解:
(1)先化简得
(2)这两个数的绝对值是
(3)先化简得
数学是思维的体操
学习赢得智慧人生
2.已知a<0,b>0且│b│>│a│,比较a,-a,b,-b的大小.
典例分析
分析:可利用数轴,先在数轴上找出a,-a,b,-b的大致位置,再根据它们在数轴上的位置进行比较.
解:由a<0,b>0可知表示a的点在原点的左边,表示b的点在原点的右边;由│b│>│a│,可知表示b的点离开原点的距离要远,如下图所示。
然后再根据两个互为相反数在数轴上所表示的点在原点两边,且关于原点对称即可得a,-a,b,-b在数轴上的位置
根据数轴上从左到右表示的数依次增大,可得:
-a
-b
0
a
b
-b
a
-a
b
所以
<
<
<
数形结合的思想
数学是思维的体操
学习赢得智慧人生
小试牛刀
1.下列判断,正确的是( )
A.若a B.若│a│<│b│,则a C.若a D.若aD
想a,b在数轴上的位置
数学是思维的体操
学习赢得智慧人生
2.下列各式中,正确的是( )
A. -|-20|>0 B. |0.2|>|-0.2|
C.|- |>-|- | D. |-3.2|<0
3.如果甲数的绝对值大于乙数的绝对值,那么( )A.甲数必定大于乙数
B.甲数必定小于乙数C.甲、乙两数一定异号D.甲、乙两数的大小,要根据具体值确定
C
D
数学是思维的体操
学习赢得智慧人生
能力提升
4.已知|a|=3,|b|=2,|c|=1,且a解:
由|a|=3,|b|=2,|c|=1得,
因为
a所以
数学是思维的体操
学习赢得智慧人生
5.有理数a,b在数轴上的表示如下图,用“>”或“<”号填空.
能力提升
(1) a_____b; (2) │a│_____│b│;(3) -a_____b;
(4) a ___-b;(5) -a ___ -b
0
1
-1
a
数学是思维的体操
学习赢得智慧人生
比较有理数大小的方法.
方法(1):数轴上表示的两个数,右边的总比左边的大.
方法(2):正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
课堂小结
数学是思维的体操
学习赢得智慧人生
课下练习:
课本第13页练习
第14页综合运用第7题
第15页拓广探索第11题
作业:课本第14页5
学习赢得智慧人生
1.2.4 绝对值
第2课时 有理数大小的比较
1.2 有理数
数学是思维的体操
学习赢得智慧人生
教学 重、难点与关键
1.重点:会利用绝对值比较有理数的大小.
2.难点:两个负数的大小比较.
3.关键:正确理解绝对值的概念
数学是思维的体操
学习赢得智慧人生
复习回顾
3.绝对值的概念
4.怎样求一个数的绝对值
5.求2题中各数的绝对值
一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
0的绝对值是0
1.数轴的定义
2.在数轴上表示以下各数
%
1
-3
-2
-1
2
3
0
%
| |
%
=
%
数学是思维的体操
学习赢得智慧人生
在小学我们学过了比较两个数的大小,把数扩充到有理数以后怎样比较两个有理数的大小呢
下图表示元旦当天我国5个城市的最低气温.
武汉4 ℃ 秦皇岛 -12℃ 上海0℃ 深圳14℃ 长春-16℃
思考:
问题:
请把这五个城市的最低气温由低到高排列
数学是思维的体操
学习赢得智慧人生
请大家思考这五个数的大小与它们在数轴上的位置有什么关系?
越 来 越 大
长春
-16℃
秦皇岛
-12℃
上海
0℃
武汉
4℃
深圳
14℃
<
<
<
<
-20 -10 -5 0 5 10
●
●
●
●
●
-12℃
-16℃
0℃
4℃
14℃
数学是思维的体操
学习赢得智慧人生
-20 -10 -5 0 5 10
●
●
●
●
●
-12℃
-16℃
0℃
4℃
14℃
数学中规定:在数轴上表示的数,它们从左到右的顺序就是从小到大的顺序
越 来 越 大
数
形
数学是思维的体操
学习赢得智慧人生
有理数的大小比较的法则
(1)正数大于0,0大于负数,正数大于一切负数
(2)两个负数,绝对值大的反而小
例如:2 0,0 -1,-3 2,-5 -3
<
<
>
>
数学是思维的体操
学习赢得智慧人生
比较两个有理数的大小的方法
1.利用数轴比较
在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
数学是思维的体操
学习赢得智慧人生
比较两个有理数的大小的方法
2.利用绝对值比较两个同号的数
两个负数,绝对值大的反而小
两个正数,绝对值大的这个数也大
归纳
异号两数比较大小,要考虑它们的正负;
同号两数比较大小,要考虑它们的绝对值。
数学是思维的体操
学习赢得智慧人生
%
比较下列各数的大小
%
1
-3
-2
-1
2
3
0
解:方法一利用数轴
方法二利用法则
%
%
数学是思维的体操
学习赢得智慧人生
典例分析
例1:比较下列各对数的大小:
(1)
(2)
(3)
解:
(1)先化简得
(2)这两个数的绝对值是
(3)先化简得
数学是思维的体操
学习赢得智慧人生
2.已知a<0,b>0且│b│>│a│,比较a,-a,b,-b的大小.
典例分析
分析:可利用数轴,先在数轴上找出a,-a,b,-b的大致位置,再根据它们在数轴上的位置进行比较.
解:由a<0,b>0可知表示a的点在原点的左边,表示b的点在原点的右边;由│b│>│a│,可知表示b的点离开原点的距离要远,如下图所示。
然后再根据两个互为相反数在数轴上所表示的点在原点两边,且关于原点对称即可得a,-a,b,-b在数轴上的位置
根据数轴上从左到右表示的数依次增大,可得:
-a
-b
0
a
b
-b
a
-a
b
所以
<
<
<
数形结合的思想
数学是思维的体操
学习赢得智慧人生
小试牛刀
1.下列判断,正确的是( )
A.若a
想a,b在数轴上的位置
数学是思维的体操
学习赢得智慧人生
2.下列各式中,正确的是( )
A. -|-20|>0 B. |0.2|>|-0.2|
C.|- |>-|- | D. |-3.2|<0
3.如果甲数的绝对值大于乙数的绝对值,那么( )A.甲数必定大于乙数
B.甲数必定小于乙数C.甲、乙两数一定异号D.甲、乙两数的大小,要根据具体值确定
C
D
数学是思维的体操
学习赢得智慧人生
能力提升
4.已知|a|=3,|b|=2,|c|=1,且a
由|a|=3,|b|=2,|c|=1得,
因为
a
数学是思维的体操
学习赢得智慧人生
5.有理数a,b在数轴上的表示如下图,用“>”或“<”号填空.
能力提升
(1) a_____b; (2) │a│_____│b│;(3) -a_____b;
(4) a ___-b;(5) -a ___ -b
0
1
-1
a
数学是思维的体操
学习赢得智慧人生
比较有理数大小的方法.
方法(1):数轴上表示的两个数,右边的总比左边的大.
方法(2):正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
课堂小结
数学是思维的体操
学习赢得智慧人生
课下练习:
课本第13页练习
第14页综合运用第7题
第15页拓广探索第11题
作业:课本第14页5
