2019-2020学年陕西省渭南市临渭区高一下学期期末数学试卷 (word解析版)
文档属性
| 名称 | 2019-2020学年陕西省渭南市临渭区高一下学期期末数学试卷 (word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 00:00:00 | ||
图片预览




文档简介
2019-2020学年陕西省渭南市临渭区高一第二学期期末数学试卷
一、选择题(共12小题).
1.cos75°cos15°+sin75°sin15°的值为( )
A.0 B. C. D.1
2.集合{α|kπ+≤α≤kπ+,k∈Z}中的角所表示的范围(阴影部分)是( )
A. B.
C. D.
3.在区间[3,18]上随机取一个数,其满足log3x≥2的概率是( )
A. B. C. D.
4.某单位有老年人27人,中年人55人,青年人81人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( )
A.简单随机抽样
B.系统抽样
C.先从中年人中剔除一人,然后分层抽样
D.先从老年人中剔除一人,然后分层抽样
5.巳知||=,||=3,|+|=3,则向量在向量方向的投影( )
A.1 B.﹣1 C.3 D.﹣3
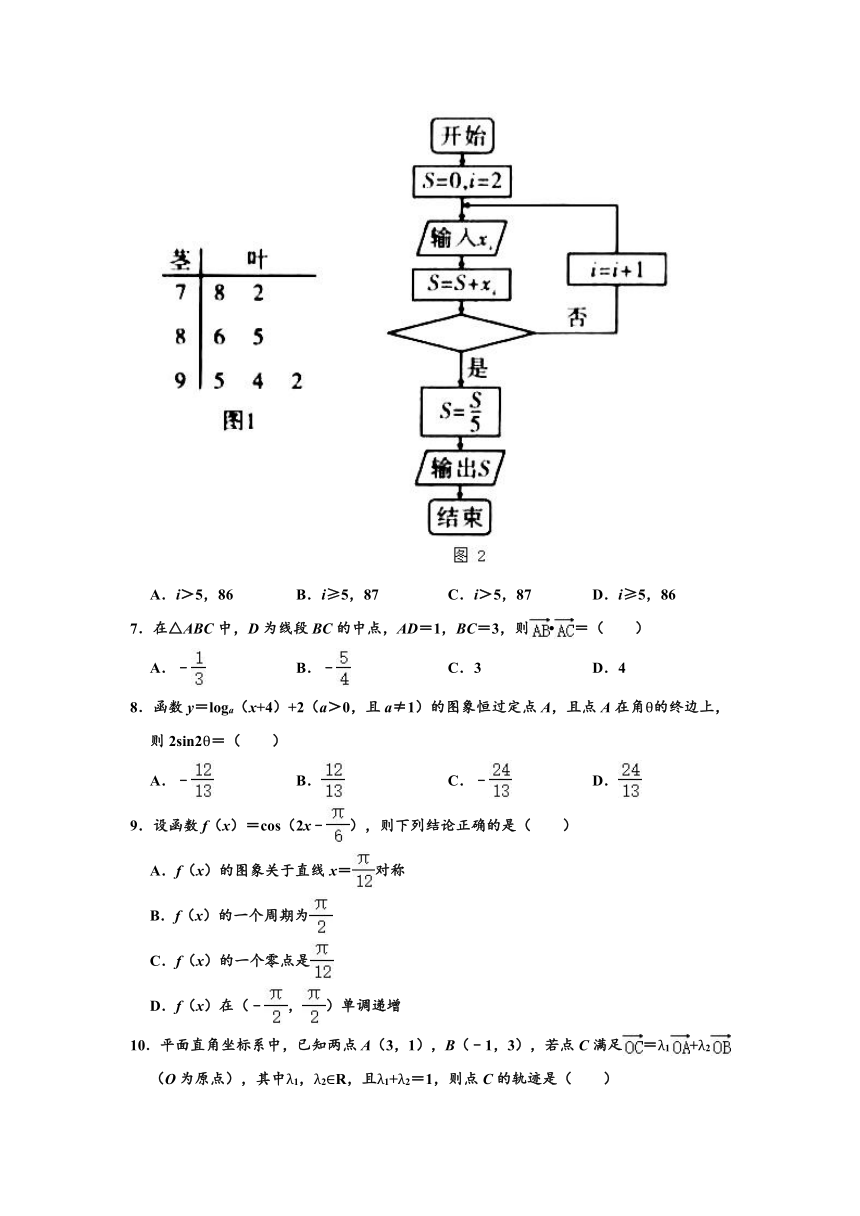
6.某校举办“中华魂”《中国梦》主题演讲比赛聘请7名评委为选手评分,评分规则是去掉一个最高分和一个最低分,再求平均分为选手的最终得分.现评委为选手赵刚的评分从低到高依次为x1,x2,……,x7,具体分数如图1的茎叶图所示,图2的程序框图是统计选手最终得分的一个算法流程图,则图中空白处及输出的S分别为( )
A.i>5,86 B.i≥5,87 C.i>5,87 D.i≥5,86
7.在△ABC中,D为线段BC的中点,AD=1,BC=3,则?=( )
A.﹣ B.﹣ C.3 D.4
8.函数y=loga(x+4)+2(a>0,且a≠1)的图象恒过定点A,且点A在角θ的终边上,则2sin2θ=( )
A.﹣ B. C.﹣ D.
9.设函数f(x)=cos(2x﹣),则下列结论正确的是( )
A.f(x)的图象关于直线x=对称
B.f(x)的一个周期为
C.f(x)的一个零点是
D.f(x)在(﹣,)单调递增
10.平面直角坐标系中,已知两点A(3,1),B(﹣1,3),若点C满足=λ1+λ2(O为原点),其中λ1,λ2∈R,且λ1+λ2=1,则点C的轨迹是( )
A.直线 B.椭圆 C.圆 D.双曲线
11.已知函数f(x)=cos(2x﹣φ),将函数f(x)的图象向右平移个单位后与函数g(x)=sin(2x﹣)的图象重合,则φ的值可以是( )
A.﹣ B.﹣ C. D.
12.已知函数f(x)=cos2(x+φ)+sin(x+φ)cos(x+φ)﹣(φ>0)的图象关于原点对称,则φ的最小值为( )
A. B. C. D.
二、填空题(本大题5小题,每小题5分,计25分,请将答案填写在答题纸中的横线上)
13.已知θ是第四象限角,且sin(θ+)=,则tan(θ﹣)= .
14.已知α∈(0,π),化简:= .
15.设=(m,2),=(2,3)且|+|2=||2+||2,则m= .
16.从2,3,8,9中任取两个不同的数字,分别记为a,b,则logab为整数的概率是 .
17.函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图所示,则f()的值为 .
三、解答题(本大题共5小题,计65分,解答应写出文字说明、证明过程或演算步骤)
18.已知向量=(3,﹣4),=(6,﹣3),=(5﹣m,﹣(3+m)).
(1)若点A,B,C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
19.已知sin2α=,.
(1)求cos2α及cosα的值;
(2)求满足条件sin(α﹣x)﹣sin(α+x)+2cosα=的锐角x.
20.已知函数f(x)=cos(2x﹣)﹣2sinxcosx.
(1)f(x)的最小正周期.
(2)求证:当x∈[﹣]时,f(x).
21.已知向量=(﹣2,1),=(x,y).
(1)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足?=﹣1的概率;
(2)若x,y在连续区间[1,6]上取值,求满足?<0的概率.
22.设函数f(x)=sin(ωx﹣)+sin(ωx﹣),其中0<ω<3,已知f()=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在[﹣,]上的最小值.
参考答案
一、选择题(共12小题).
1.cos75°cos15°+sin75°sin15°的值为( )
A.0 B. C. D.1
【分析】由条件利用两角和的正弦公式,计算求得结果.
解:∵cos75°cos15°+sin75°sin15°=cos(75°﹣15°)=cos60°=,
故选:B.
2.集合{α|kπ+≤α≤kπ+,k∈Z}中的角所表示的范围(阴影部分)是( )
A. B.
C. D.
【分析】先看当k取偶数时,角的终边所在的象限,再看当k取奇数时,角的终边所在的象限,把二者的范围取并集.
解:当k取偶数时,比如k=0时,≤α≤,故角的终边在第一象限.
当k取奇数时,比如k=1时,≤α≤,故角的终边在第三象限.
综上,角的终边在第一、或第三象限,
故选:C.
3.在区间[3,18]上随机取一个数,其满足log3x≥2的概率是( )
A. B. C. D.
【分析】根据对数的性质求出对数不等式的等价条件,结合几何概型的概率公式进行计算即可.
解:当3≤x≤18时,由log3x≥2得9≤x≤18,
则对应的概率P===,
故选:B.
4.某单位有老年人27人,中年人55人,青年人81人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( )
A.简单随机抽样
B.系统抽样
C.先从中年人中剔除一人,然后分层抽样
D.先从老年人中剔除一人,然后分层抽样
【分析】由于总体由三部分构成,所以采用分层抽样完成.
解:由于总体由三部分构成,所以采用分层抽样完成.
分层抽样直接算结果不是整数,所以先从中年人中剔除一人,然后在分层.
此时每个个体被抽到的概率等于
老年人抽取27×人,中年人54×人,青年人81×人.
故选:C.
5.巳知||=,||=3,|+|=3,则向量在向量方向的投影( )
A.1 B.﹣1 C.3 D.﹣3
【分析】根据平面向量的数量积与投影的定义,计算即可.
解:由||=,||=3,|+|=3,
所以(+)2=+2+=3+2+9=18,
解得=3;
所以向量在向量方向的投影为:==1.
故选:A.
6.某校举办“中华魂”《中国梦》主题演讲比赛聘请7名评委为选手评分,评分规则是去掉一个最高分和一个最低分,再求平均分为选手的最终得分.现评委为选手赵刚的评分从低到高依次为x1,x2,……,x7,具体分数如图1的茎叶图所示,图2的程序框图是统计选手最终得分的一个算法流程图,则图中空白处及输出的S分别为( )
A.i>5,86 B.i≥5,87 C.i>5,87 D.i≥5,86
【分析】该程序运行后是计算5个数据的平均数,由此求出对应的结果.
解:模拟程序的运行过程知,该程序运行后是计算5个数据的平均数,所以i>5,
由5个数据分别是78、86、85、92、94,
计算平均数为=×(78+85+86+92+94)=87.
故选:C.
7.在△ABC中,D为线段BC的中点,AD=1,BC=3,则?=( )
A.﹣ B.﹣ C.3 D.4
【分析】以,为基底,分别表示,,即可求解.
解:∵D为线段BC的中点,∴,=﹣=﹣(),
又AD=1,BC=3,则,.
∴?=﹣()()=﹣()=﹣()=﹣.
故选:B.
8.函数y=loga(x+4)+2(a>0,且a≠1)的图象恒过定点A,且点A在角θ的终边上,则2sin2θ=( )
A.﹣ B. C.﹣ D.
【分析】先求出定点A的坐标,再利用任意角的三角函数的定义,二倍角的正弦公式,求出2sin2θ的值.
解:对于函数y=loga(x+4)+2(a>0,且a≠1),
令x+4=1,求得x=﹣3,y=2,可得它的的图象恒过定点A(﹣3,2),
且点A在角θ的终边上,∴sinθ==,cosθ==﹣,
则2sin2θ=4sinθcosθ=4×?(﹣)=﹣,
故选:C.
9.设函数f(x)=cos(2x﹣),则下列结论正确的是( )
A.f(x)的图象关于直线x=对称
B.f(x)的一个周期为
C.f(x)的一个零点是
D.f(x)在(﹣,)单调递增
【分析】A,由f()取得最值判定;
B,根据T=求得周期,即可判定;
C,由x=时,f(x)=f(0)=1≠0,即可判定;
D,根据周期为π,即可判定f(x)在(﹣,)不单调.
解:对于A,x=时,f(x)=f(0)=1,函数取得最值,故A正确;
对于B,T==π,故错;
对于C,x=时,f(x)=f(0)=1≠0,故错;
对于D,∵f(x)的周期T=π,∴f(x)在(﹣,)不单调,故错.
故选:A.
10.平面直角坐标系中,已知两点A(3,1),B(﹣1,3),若点C满足=λ1+λ2(O为原点),其中λ1,λ2∈R,且λ1+λ2=1,则点C的轨迹是( )
A.直线 B.椭圆 C.圆 D.双曲线
【分析】设C(x,y),欲求点C的轨迹,只须求出坐标x,y的关系式即可,先依据向量的坐标运算表示出x,y,再消去λ1,λ2即得.
解:设C(x,y),则=(x,y),=(3,1),=(﹣1,3),
∵=λ1+λ2,
∴,又λ1+λ2=1,
∴x+2y﹣5=0,表示一条直线.
故选:A.
11.已知函数f(x)=cos(2x﹣φ),将函数f(x)的图象向右平移个单位后与函数g(x)=sin(2x﹣)的图象重合,则φ的值可以是( )
A.﹣ B.﹣ C. D.
【分析】直接利用三角函数关系式的平移变换和诱导公式的应用求出等量关系式,进一步求出结果.
解:函数f(x)=cos(2x﹣φ),将函数f(x)的图象向右平移个单位后得到h(x)=cos(2x﹣﹣φ)=sin(2x﹣﹣φ)=g(x)=sin(2x﹣),
所以φ=(k∈Z),
整理得φ=2kπ+,
当k=﹣1时,φ=.
故选:B.
12.已知函数f(x)=cos2(x+φ)+sin(x+φ)cos(x+φ)﹣(φ>0)的图象关于原点对称,则φ的最小值为( )
A. B. C. D.
【分析】利用二倍角公式,两角和的正弦函数公式化简函数解析式可得f(x)=sin(2x+2φ+),利用正弦函数的对称性可得2φ+=kπ,k∈Z,结合φ的范围即可求解φ的最小值.
解:f(x)=cos2(x+φ)+sin(x+φ)cos(x+φ)﹣
=(1+cos2(x+φ))+sin2(x+φ)﹣
=cos2(x+φ)+sin2(x+φ)
=sin(2x+2φ+),
∵f(x)的图象关于原点对称,
∴2φ+=kπ,k∈Z,解得φ=kπ﹣,k∈Z,
∵φ>0,
∴φ的最小值为.
故选:A.
二、填空题(本大题5小题,每小题5分,计25分,请将答案填写在答题纸中的横线上)
13.已知θ是第四象限角,且sin(θ+)=,则tan(θ﹣)= .
【分析】由θ得范围求得θ+的范围,结合已知求得cos(θ+),再由诱导公式求得sin()及cos(),进一步由诱导公式及同角三角函数基本关系式求得tan(θ﹣)的值.
解:∵θ是第四象限角,
∴,则,
又sin(θ+)=,
∴cos(θ+)=.
∴cos()=sin(θ+)=,sin()=cos(θ+)=.
则tan(θ﹣)=﹣tan()=﹣=.
故答案为:﹣.
14.已知α∈(0,π),化简:= cosα .
【分析】由条件利用二倍角公式、以及三角函数在各个象限内的符号,化简要求的式子,可得结果.
解:∵α∈(0,π),∴=
===cosα,
故答案为:cosα.
15.设=(m,2),=(2,3)且|+|2=||2+||2,则m= ﹣3 .
【分析】根据题意,由数量积的运算性质可得?=0,然后由?=2m+6=0,解可得m的值.
解:根据题意,|+|2=(+)2=||2+||2+2?,
若|+|2=||2+||2,则有?=0,
又由=(m,2),=(2,3),得?=2m+6=0,
所以m=﹣3.
故答案为:﹣3.
16.从2,3,8,9中任取两个不同的数字,分别记为a,b,则logab为整数的概率是 .
【分析】由已知条件先求出基本事件总数,再利用列举法求出logab为整数满足的基本事件个数,由此能求出logab为整数的概率.
解:从2,3,8,9中任取两个不同的数字,分别记为a,b,
基本事件总数n==12,
logab为整数满足的基本事件个数为(2,8),(3,9),共2个,
∴logab为整数的概率p=.
故答案为:.
17.函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图所示,则f()的值为 .
【分析】根据图象求出A,ω 和φ,即可求函数f(x)的解析式;可求f()的值
解::(1)由题设图象知,A=2,周期T=(﹣),解得:T=π.
∴ω==2.
∵点(,2)在函数图象上,
∴2sin(2×+φ)=2,即sin(+φ)=1.
∵0<φ<π,
∴φ=.
故得f(x)=2sin(2x),
那么f()=2sin(2×)=
故答案为:.
三、解答题(本大题共5小题,计65分,解答应写出文字说明、证明过程或演算步骤)
18.已知向量=(3,﹣4),=(6,﹣3),=(5﹣m,﹣(3+m)).
(1)若点A,B,C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
【分析】(1)根据三点构成三角形的条件,即只要三点不共线,根据共线的条件确定出m的值,从而解出A、B、C能构成三角形时,实数m满足的条件;
(2)将几何中的角为直角转化为向量的语言,通过向量的数量积为零列出关于实数m的方程,求解出实数m.
解:(1)若点A、B、C能构成三角形,则这三点不共线,
∵,故知3(1﹣m)≠2﹣m
∴实数时,满足条件.
(2)若△ABC为直角三角形,且∠A为直角,则,
∴3(2﹣m)+(1﹣m)=0
解得.
19.已知sin2α=,.
(1)求cos2α及cosα的值;
(2)求满足条件sin(α﹣x)﹣sin(α+x)+2cosα=的锐角x.
【分析】(1)利用α的范围,求出2α的范围,然后求出cos2α,通过二倍角公式求出cosα的值.
(2)通过已知表达式,求出sinx的值,推出结果即可.
解:(1)因为,所以.…(1分)
又sin2α=.
因此cos2α=﹣=.…
由cos2α=2cos2α﹣1,得cosα=﹣.…
(2)因为sin(α﹣x)﹣sin(α+x)+2cosα=﹣,
所以2cosα(1﹣sinx)=﹣,所以sinx=.…
因为x为锐角,所以x=.…
20.已知函数f(x)=cos(2x﹣)﹣2sinxcosx.
(1)f(x)的最小正周期.
(2)求证:当x∈[﹣]时,f(x).
【分析】(1)利用和与差和二倍角公式化简,结合三角函数的图象及性质可得f(x)的最小正周期.
(2)当x∈[﹣]时,求解内层函数的范围,可知f(x)的最小值,可得f(x).
解:(1)函数f(x)=cos(2x﹣)﹣2sinxcosx.
即f(x)=(cos2xcos+sin2xsin)﹣sin2x=cos2x+sin2x=sin(2x+)
∴f(x)的最小正周期T=.
(2)当x∈[﹣]时,
∴2x+∈[,]
当2x+=时,f(x)取得最小值为.
即当x∈[﹣]时,f(x).
21.已知向量=(﹣2,1),=(x,y).
(1)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足?=﹣1的概率;
(2)若x,y在连续区间[1,6]上取值,求满足?<0的概率.
【分析】(1)根据题意,求出满足条件=﹣1的基本事件个数及总的基本事件个数,
代入古典概型公式进行计算求解即可;
(2)根据题意,画出满足条件?<0的图形,结合图形找出满足条件的点集对应的图形面积,
利用几何概型的概率公式计算即可.
解:(1)将一枚质地均匀的正方体骰子先后抛掷两次,所包含的基本事件总数为6×6=36个;
由?=﹣1,得﹣2x+y=﹣1,∴满足a?b=﹣1的基本事件为(1,1),(2,3),(3,5)共3个;
∴满足?=﹣1的概率为P==;
(2)若x,y在连续区间[1,6]上取值,则全部基本事件的结果为Ω={(x,y)|1≤x≤6,1≤y≤6};
满足?<0的基本事件的结果为A={(x,y)|1≤x≤6,1≤y≤6且﹣2x+y<0};
画出图形如图所示,
则矩形的面积为S矩形=25,
阴影部分的面积为S阴影=25﹣×2×4=21,
∴满足?<0的概率为P=.
22.设函数f(x)=sin(ωx﹣)+sin(ωx﹣),其中0<ω<3,已知f()=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在[﹣,]上的最小值.
【分析】(Ⅰ)利用三角恒等变换化函数f(x)为正弦型函数,根据f()=0求出ω的值;
(Ⅱ)写出f(x)解析式,利用平移法则写出g(x)的解析式,求出x∈[﹣,]时g(x)的最小值.
解:(Ⅰ)函数f(x)=sin(ωx﹣)+sin(ωx﹣)
=sinωxcos﹣cosωxsin﹣sin(﹣ωx)
=sinωx﹣cosωx
=sin(ωx﹣),
又f()=sin(ω﹣)=0,
∴ω﹣=kπ,k∈Z,
解得ω=6k+2,
又0<ω<3,
∴ω=2;
(Ⅱ)由(Ⅰ)知,f(x)=sin(2x﹣),
将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得到函数y=sin(x﹣)的图象;
再将得到的图象向左平移个单位,得到y=sin(x+﹣)的图象,
∴函数y=g(x)=sin(x﹣);
当x∈[﹣,]时,x﹣∈[﹣,],
∴sin(x﹣)∈[﹣,1],
∴当x=﹣时,g(x)取得最小值是﹣×=﹣.
一、选择题(共12小题).
1.cos75°cos15°+sin75°sin15°的值为( )
A.0 B. C. D.1
2.集合{α|kπ+≤α≤kπ+,k∈Z}中的角所表示的范围(阴影部分)是( )
A. B.
C. D.
3.在区间[3,18]上随机取一个数,其满足log3x≥2的概率是( )
A. B. C. D.
4.某单位有老年人27人,中年人55人,青年人81人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( )
A.简单随机抽样
B.系统抽样
C.先从中年人中剔除一人,然后分层抽样
D.先从老年人中剔除一人,然后分层抽样
5.巳知||=,||=3,|+|=3,则向量在向量方向的投影( )
A.1 B.﹣1 C.3 D.﹣3
6.某校举办“中华魂”《中国梦》主题演讲比赛聘请7名评委为选手评分,评分规则是去掉一个最高分和一个最低分,再求平均分为选手的最终得分.现评委为选手赵刚的评分从低到高依次为x1,x2,……,x7,具体分数如图1的茎叶图所示,图2的程序框图是统计选手最终得分的一个算法流程图,则图中空白处及输出的S分别为( )
A.i>5,86 B.i≥5,87 C.i>5,87 D.i≥5,86
7.在△ABC中,D为线段BC的中点,AD=1,BC=3,则?=( )
A.﹣ B.﹣ C.3 D.4
8.函数y=loga(x+4)+2(a>0,且a≠1)的图象恒过定点A,且点A在角θ的终边上,则2sin2θ=( )
A.﹣ B. C.﹣ D.
9.设函数f(x)=cos(2x﹣),则下列结论正确的是( )
A.f(x)的图象关于直线x=对称
B.f(x)的一个周期为
C.f(x)的一个零点是
D.f(x)在(﹣,)单调递增
10.平面直角坐标系中,已知两点A(3,1),B(﹣1,3),若点C满足=λ1+λ2(O为原点),其中λ1,λ2∈R,且λ1+λ2=1,则点C的轨迹是( )
A.直线 B.椭圆 C.圆 D.双曲线
11.已知函数f(x)=cos(2x﹣φ),将函数f(x)的图象向右平移个单位后与函数g(x)=sin(2x﹣)的图象重合,则φ的值可以是( )
A.﹣ B.﹣ C. D.
12.已知函数f(x)=cos2(x+φ)+sin(x+φ)cos(x+φ)﹣(φ>0)的图象关于原点对称,则φ的最小值为( )
A. B. C. D.
二、填空题(本大题5小题,每小题5分,计25分,请将答案填写在答题纸中的横线上)
13.已知θ是第四象限角,且sin(θ+)=,则tan(θ﹣)= .
14.已知α∈(0,π),化简:= .
15.设=(m,2),=(2,3)且|+|2=||2+||2,则m= .
16.从2,3,8,9中任取两个不同的数字,分别记为a,b,则logab为整数的概率是 .
17.函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图所示,则f()的值为 .
三、解答题(本大题共5小题,计65分,解答应写出文字说明、证明过程或演算步骤)
18.已知向量=(3,﹣4),=(6,﹣3),=(5﹣m,﹣(3+m)).
(1)若点A,B,C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
19.已知sin2α=,.
(1)求cos2α及cosα的值;
(2)求满足条件sin(α﹣x)﹣sin(α+x)+2cosα=的锐角x.
20.已知函数f(x)=cos(2x﹣)﹣2sinxcosx.
(1)f(x)的最小正周期.
(2)求证:当x∈[﹣]时,f(x).
21.已知向量=(﹣2,1),=(x,y).
(1)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足?=﹣1的概率;
(2)若x,y在连续区间[1,6]上取值,求满足?<0的概率.
22.设函数f(x)=sin(ωx﹣)+sin(ωx﹣),其中0<ω<3,已知f()=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在[﹣,]上的最小值.
参考答案
一、选择题(共12小题).
1.cos75°cos15°+sin75°sin15°的值为( )
A.0 B. C. D.1
【分析】由条件利用两角和的正弦公式,计算求得结果.
解:∵cos75°cos15°+sin75°sin15°=cos(75°﹣15°)=cos60°=,
故选:B.
2.集合{α|kπ+≤α≤kπ+,k∈Z}中的角所表示的范围(阴影部分)是( )
A. B.
C. D.
【分析】先看当k取偶数时,角的终边所在的象限,再看当k取奇数时,角的终边所在的象限,把二者的范围取并集.
解:当k取偶数时,比如k=0时,≤α≤,故角的终边在第一象限.
当k取奇数时,比如k=1时,≤α≤,故角的终边在第三象限.
综上,角的终边在第一、或第三象限,
故选:C.
3.在区间[3,18]上随机取一个数,其满足log3x≥2的概率是( )
A. B. C. D.
【分析】根据对数的性质求出对数不等式的等价条件,结合几何概型的概率公式进行计算即可.
解:当3≤x≤18时,由log3x≥2得9≤x≤18,
则对应的概率P===,
故选:B.
4.某单位有老年人27人,中年人55人,青年人81人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( )
A.简单随机抽样
B.系统抽样
C.先从中年人中剔除一人,然后分层抽样
D.先从老年人中剔除一人,然后分层抽样
【分析】由于总体由三部分构成,所以采用分层抽样完成.
解:由于总体由三部分构成,所以采用分层抽样完成.
分层抽样直接算结果不是整数,所以先从中年人中剔除一人,然后在分层.
此时每个个体被抽到的概率等于
老年人抽取27×人,中年人54×人,青年人81×人.
故选:C.
5.巳知||=,||=3,|+|=3,则向量在向量方向的投影( )
A.1 B.﹣1 C.3 D.﹣3
【分析】根据平面向量的数量积与投影的定义,计算即可.
解:由||=,||=3,|+|=3,
所以(+)2=+2+=3+2+9=18,
解得=3;
所以向量在向量方向的投影为:==1.
故选:A.
6.某校举办“中华魂”《中国梦》主题演讲比赛聘请7名评委为选手评分,评分规则是去掉一个最高分和一个最低分,再求平均分为选手的最终得分.现评委为选手赵刚的评分从低到高依次为x1,x2,……,x7,具体分数如图1的茎叶图所示,图2的程序框图是统计选手最终得分的一个算法流程图,则图中空白处及输出的S分别为( )
A.i>5,86 B.i≥5,87 C.i>5,87 D.i≥5,86
【分析】该程序运行后是计算5个数据的平均数,由此求出对应的结果.
解:模拟程序的运行过程知,该程序运行后是计算5个数据的平均数,所以i>5,
由5个数据分别是78、86、85、92、94,
计算平均数为=×(78+85+86+92+94)=87.
故选:C.
7.在△ABC中,D为线段BC的中点,AD=1,BC=3,则?=( )
A.﹣ B.﹣ C.3 D.4
【分析】以,为基底,分别表示,,即可求解.
解:∵D为线段BC的中点,∴,=﹣=﹣(),
又AD=1,BC=3,则,.
∴?=﹣()()=﹣()=﹣()=﹣.
故选:B.
8.函数y=loga(x+4)+2(a>0,且a≠1)的图象恒过定点A,且点A在角θ的终边上,则2sin2θ=( )
A.﹣ B. C.﹣ D.
【分析】先求出定点A的坐标,再利用任意角的三角函数的定义,二倍角的正弦公式,求出2sin2θ的值.
解:对于函数y=loga(x+4)+2(a>0,且a≠1),
令x+4=1,求得x=﹣3,y=2,可得它的的图象恒过定点A(﹣3,2),
且点A在角θ的终边上,∴sinθ==,cosθ==﹣,
则2sin2θ=4sinθcosθ=4×?(﹣)=﹣,
故选:C.
9.设函数f(x)=cos(2x﹣),则下列结论正确的是( )
A.f(x)的图象关于直线x=对称
B.f(x)的一个周期为
C.f(x)的一个零点是
D.f(x)在(﹣,)单调递增
【分析】A,由f()取得最值判定;
B,根据T=求得周期,即可判定;
C,由x=时,f(x)=f(0)=1≠0,即可判定;
D,根据周期为π,即可判定f(x)在(﹣,)不单调.
解:对于A,x=时,f(x)=f(0)=1,函数取得最值,故A正确;
对于B,T==π,故错;
对于C,x=时,f(x)=f(0)=1≠0,故错;
对于D,∵f(x)的周期T=π,∴f(x)在(﹣,)不单调,故错.
故选:A.
10.平面直角坐标系中,已知两点A(3,1),B(﹣1,3),若点C满足=λ1+λ2(O为原点),其中λ1,λ2∈R,且λ1+λ2=1,则点C的轨迹是( )
A.直线 B.椭圆 C.圆 D.双曲线
【分析】设C(x,y),欲求点C的轨迹,只须求出坐标x,y的关系式即可,先依据向量的坐标运算表示出x,y,再消去λ1,λ2即得.
解:设C(x,y),则=(x,y),=(3,1),=(﹣1,3),
∵=λ1+λ2,
∴,又λ1+λ2=1,
∴x+2y﹣5=0,表示一条直线.
故选:A.
11.已知函数f(x)=cos(2x﹣φ),将函数f(x)的图象向右平移个单位后与函数g(x)=sin(2x﹣)的图象重合,则φ的值可以是( )
A.﹣ B.﹣ C. D.
【分析】直接利用三角函数关系式的平移变换和诱导公式的应用求出等量关系式,进一步求出结果.
解:函数f(x)=cos(2x﹣φ),将函数f(x)的图象向右平移个单位后得到h(x)=cos(2x﹣﹣φ)=sin(2x﹣﹣φ)=g(x)=sin(2x﹣),
所以φ=(k∈Z),
整理得φ=2kπ+,
当k=﹣1时,φ=.
故选:B.
12.已知函数f(x)=cos2(x+φ)+sin(x+φ)cos(x+φ)﹣(φ>0)的图象关于原点对称,则φ的最小值为( )
A. B. C. D.
【分析】利用二倍角公式,两角和的正弦函数公式化简函数解析式可得f(x)=sin(2x+2φ+),利用正弦函数的对称性可得2φ+=kπ,k∈Z,结合φ的范围即可求解φ的最小值.
解:f(x)=cos2(x+φ)+sin(x+φ)cos(x+φ)﹣
=(1+cos2(x+φ))+sin2(x+φ)﹣
=cos2(x+φ)+sin2(x+φ)
=sin(2x+2φ+),
∵f(x)的图象关于原点对称,
∴2φ+=kπ,k∈Z,解得φ=kπ﹣,k∈Z,
∵φ>0,
∴φ的最小值为.
故选:A.
二、填空题(本大题5小题,每小题5分,计25分,请将答案填写在答题纸中的横线上)
13.已知θ是第四象限角,且sin(θ+)=,则tan(θ﹣)= .
【分析】由θ得范围求得θ+的范围,结合已知求得cos(θ+),再由诱导公式求得sin()及cos(),进一步由诱导公式及同角三角函数基本关系式求得tan(θ﹣)的值.
解:∵θ是第四象限角,
∴,则,
又sin(θ+)=,
∴cos(θ+)=.
∴cos()=sin(θ+)=,sin()=cos(θ+)=.
则tan(θ﹣)=﹣tan()=﹣=.
故答案为:﹣.
14.已知α∈(0,π),化简:= cosα .
【分析】由条件利用二倍角公式、以及三角函数在各个象限内的符号,化简要求的式子,可得结果.
解:∵α∈(0,π),∴=
===cosα,
故答案为:cosα.
15.设=(m,2),=(2,3)且|+|2=||2+||2,则m= ﹣3 .
【分析】根据题意,由数量积的运算性质可得?=0,然后由?=2m+6=0,解可得m的值.
解:根据题意,|+|2=(+)2=||2+||2+2?,
若|+|2=||2+||2,则有?=0,
又由=(m,2),=(2,3),得?=2m+6=0,
所以m=﹣3.
故答案为:﹣3.
16.从2,3,8,9中任取两个不同的数字,分别记为a,b,则logab为整数的概率是 .
【分析】由已知条件先求出基本事件总数,再利用列举法求出logab为整数满足的基本事件个数,由此能求出logab为整数的概率.
解:从2,3,8,9中任取两个不同的数字,分别记为a,b,
基本事件总数n==12,
logab为整数满足的基本事件个数为(2,8),(3,9),共2个,
∴logab为整数的概率p=.
故答案为:.
17.函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图所示,则f()的值为 .
【分析】根据图象求出A,ω 和φ,即可求函数f(x)的解析式;可求f()的值
解::(1)由题设图象知,A=2,周期T=(﹣),解得:T=π.
∴ω==2.
∵点(,2)在函数图象上,
∴2sin(2×+φ)=2,即sin(+φ)=1.
∵0<φ<π,
∴φ=.
故得f(x)=2sin(2x),
那么f()=2sin(2×)=
故答案为:.
三、解答题(本大题共5小题,计65分,解答应写出文字说明、证明过程或演算步骤)
18.已知向量=(3,﹣4),=(6,﹣3),=(5﹣m,﹣(3+m)).
(1)若点A,B,C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
【分析】(1)根据三点构成三角形的条件,即只要三点不共线,根据共线的条件确定出m的值,从而解出A、B、C能构成三角形时,实数m满足的条件;
(2)将几何中的角为直角转化为向量的语言,通过向量的数量积为零列出关于实数m的方程,求解出实数m.
解:(1)若点A、B、C能构成三角形,则这三点不共线,
∵,故知3(1﹣m)≠2﹣m
∴实数时,满足条件.
(2)若△ABC为直角三角形,且∠A为直角,则,
∴3(2﹣m)+(1﹣m)=0
解得.
19.已知sin2α=,.
(1)求cos2α及cosα的值;
(2)求满足条件sin(α﹣x)﹣sin(α+x)+2cosα=的锐角x.
【分析】(1)利用α的范围,求出2α的范围,然后求出cos2α,通过二倍角公式求出cosα的值.
(2)通过已知表达式,求出sinx的值,推出结果即可.
解:(1)因为,所以.…(1分)
又sin2α=.
因此cos2α=﹣=.…
由cos2α=2cos2α﹣1,得cosα=﹣.…
(2)因为sin(α﹣x)﹣sin(α+x)+2cosα=﹣,
所以2cosα(1﹣sinx)=﹣,所以sinx=.…
因为x为锐角,所以x=.…
20.已知函数f(x)=cos(2x﹣)﹣2sinxcosx.
(1)f(x)的最小正周期.
(2)求证:当x∈[﹣]时,f(x).
【分析】(1)利用和与差和二倍角公式化简,结合三角函数的图象及性质可得f(x)的最小正周期.
(2)当x∈[﹣]时,求解内层函数的范围,可知f(x)的最小值,可得f(x).
解:(1)函数f(x)=cos(2x﹣)﹣2sinxcosx.
即f(x)=(cos2xcos+sin2xsin)﹣sin2x=cos2x+sin2x=sin(2x+)
∴f(x)的最小正周期T=.
(2)当x∈[﹣]时,
∴2x+∈[,]
当2x+=时,f(x)取得最小值为.
即当x∈[﹣]时,f(x).
21.已知向量=(﹣2,1),=(x,y).
(1)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足?=﹣1的概率;
(2)若x,y在连续区间[1,6]上取值,求满足?<0的概率.
【分析】(1)根据题意,求出满足条件=﹣1的基本事件个数及总的基本事件个数,
代入古典概型公式进行计算求解即可;
(2)根据题意,画出满足条件?<0的图形,结合图形找出满足条件的点集对应的图形面积,
利用几何概型的概率公式计算即可.
解:(1)将一枚质地均匀的正方体骰子先后抛掷两次,所包含的基本事件总数为6×6=36个;
由?=﹣1,得﹣2x+y=﹣1,∴满足a?b=﹣1的基本事件为(1,1),(2,3),(3,5)共3个;
∴满足?=﹣1的概率为P==;
(2)若x,y在连续区间[1,6]上取值,则全部基本事件的结果为Ω={(x,y)|1≤x≤6,1≤y≤6};
满足?<0的基本事件的结果为A={(x,y)|1≤x≤6,1≤y≤6且﹣2x+y<0};
画出图形如图所示,
则矩形的面积为S矩形=25,
阴影部分的面积为S阴影=25﹣×2×4=21,
∴满足?<0的概率为P=.
22.设函数f(x)=sin(ωx﹣)+sin(ωx﹣),其中0<ω<3,已知f()=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在[﹣,]上的最小值.
【分析】(Ⅰ)利用三角恒等变换化函数f(x)为正弦型函数,根据f()=0求出ω的值;
(Ⅱ)写出f(x)解析式,利用平移法则写出g(x)的解析式,求出x∈[﹣,]时g(x)的最小值.
解:(Ⅰ)函数f(x)=sin(ωx﹣)+sin(ωx﹣)
=sinωxcos﹣cosωxsin﹣sin(﹣ωx)
=sinωx﹣cosωx
=sin(ωx﹣),
又f()=sin(ω﹣)=0,
∴ω﹣=kπ,k∈Z,
解得ω=6k+2,
又0<ω<3,
∴ω=2;
(Ⅱ)由(Ⅰ)知,f(x)=sin(2x﹣),
将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得到函数y=sin(x﹣)的图象;
再将得到的图象向左平移个单位,得到y=sin(x+﹣)的图象,
∴函数y=g(x)=sin(x﹣);
当x∈[﹣,]时,x﹣∈[﹣,],
∴sin(x﹣)∈[﹣,1],
∴当x=﹣时,g(x)取得最小值是﹣×=﹣.
同课章节目录
