人教版七年级数学上册 1.3.1有理数的加法课件(第一课时)(31张PPT)
文档属性
| 名称 | 人教版七年级数学上册 1.3.1有理数的加法课件(第一课时)(31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 436.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 00:00:00 | ||
图片预览









文档简介
第一章 有理数
1.3.1有理数的加法
第一课时
【学习目标】
掌握有理数加法法则,能熟练进行有理数加法运算;
01
理解有理数加法意义
02
能利用有理数加法运算解决简单的实际问题。
03
【课前预习】
1.计算(﹣3)+5的结果等于( )
A.2 B.﹣2 C.8 D.﹣8
2.若|m|=3,|n|=5,且m-n>0,则m+n的值是( )
A.-2 B.-8或8 C.-8或-2 D.8或-2
3.有理数、在数轴上的位置如图所示,则的值( )
A.大于 B.小于 C.小于 D.大于
4.下面结论正确的有( )
①两个有理数相加,和一定大于每一个加数.
②一个正数与一个负数相加得正数.
③两个负数和的绝对值一定等于它们绝对值的和.
④两个正数相加,和为正数.
⑤两个负数相加,绝对值相减.
⑥正数加负数,其和一定等于0.
A.0个 B.1个 C.2个 D.3个
5.如果两个数的和是负数,那么这两个数( )
A.至少有一个为正数 B.同是正数 C.同是负数 D.至少有一个为负数
【课前预习】答案
1.A
2.C
3.A
4.C
5.D
【学习探究】
小青在一条东西向的跑道上,先走了5米,又走了3米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
因为小明最后的位置与行走方向有关!
规定: 向东为正 向西为负
1、 向东走5米,再向东走3米,两次一共向东走了多少米 ?
-1 0 1 2 3 4 5 6 7 8
(+5)+(+3)=8
5
3
东
西
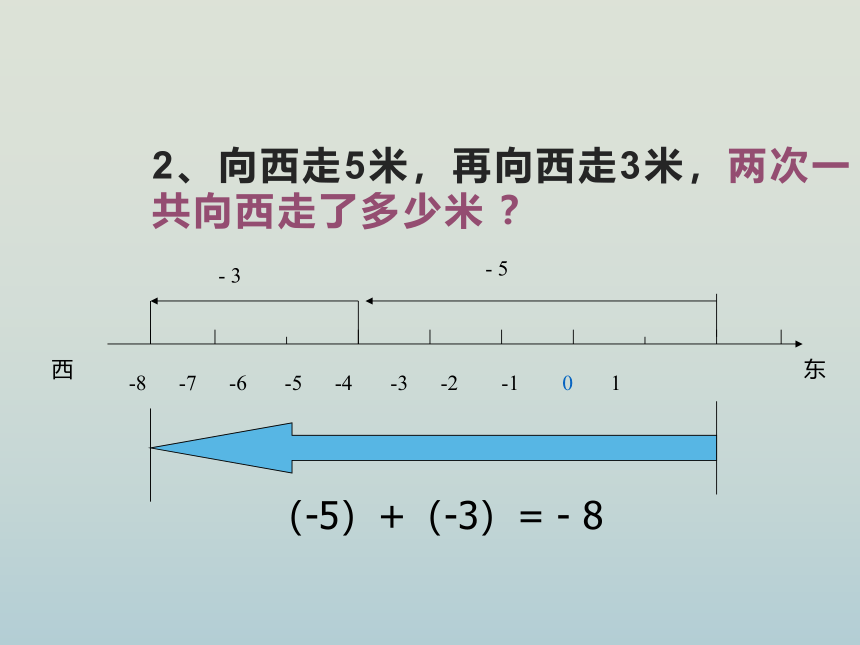
2、向西走5米,再向西走3米,两次一共向西走了多少米 ?
-8 -7 -6 -5 -4 -3 -2 -1 0 1
- 3
- 5
(-5)+(-3)= - 8
东
西
3、 向东走5米,再向西走3米,两次一共向东走了多少米 ?
(+5)+(-3)=2
-1 0 1 2 3 4 5 6
5
-3
东
西
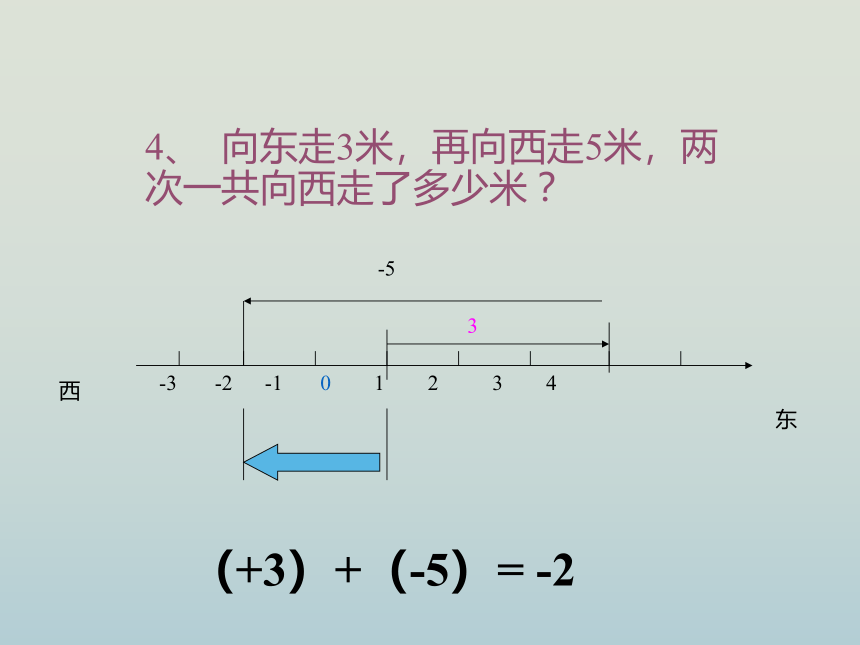
4、 向东走3米,再向西走5米,两 次一共向西走了多少米 ?
(+3)+(-5)= -2
-3 -2 -1 0 1 2 3 4
3
-5
东
西
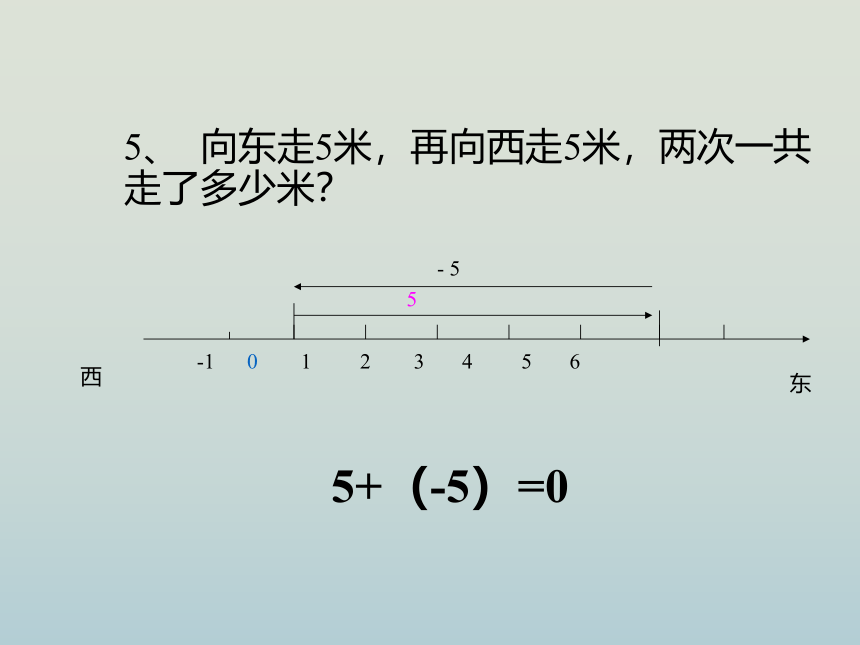
5、 向东走5米,再向西走5米,两次一共 走了多少米?
5+(-5)=0
-1 0 1 2 3 4 5 6
- 5
5
东
西
6、 向西走5米,再向东走0米, 两次一共向西走了多少米?
(-5)+0= - 5
-5 -4 -3 -2 -1 0 1
-5
东
西
( - 7 ) + ( -6 ) = - 13
( - 8 ) + ( -6 ) = - 14
(+5) + ( + 15) = +20
(+9) + (+ 3) = + 12
从得数中你能发现它的符号有规律吗?
同号两数相加,取相同的符号,
并把绝对值相加.
规律
(2) (-3)+(-9)
= -(3+9)= -12
(3) (-13)+(-8)
= -(13+8)= -21
(1) 6 + 11
= +(6+11)= 17
(1) 6 + 11
(2)(-3)+(-9)
(3)(-13)+(-8)
解:
练习
(+ 5) + ( -3 ) = +2
(+3) + ( -5 ) = - 2
( +5) + ( - 9 ) = - 4
(- 11) + (+4 ) = - 7
从得数中你能发现它的符号有规律吗?
绝对值不相等的异号两数相加,
取绝对值较大的数的符号,
并用较大的绝对值减去较小的绝对值.
规律
(1) (-3)+ 9
(4)(-4.7)+ 3.9
= +(9-3)= 6
=-(4.7-3.9)= -0.8
(2) 10 + (-6)
(3) +(- )
= +(10-6) = 4
2
1
3
2
=-( - )= -
3
2
2
1
6
1
(1) (-3)+ 9
(2) 10 + (-6)
(3) +(- )
2
1
3
2
解:
(4)(-4.7)+ 3.9
练习
(+5)+(-5)=0
互为相反数的两个数相加得0
(-5)+0=-5
一个数同0相加,仍得这个数
规律
(1) -79+79
(2) 12+(-12)
= 0
= 0
(3) 5+0
(4) (-3)+0
= 5
= -3
练习
有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加
数的符号,并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得0.
3. —个数同0相加,仍得这个数.
例1 计算:
(1)(-4)+(-8);(2)(-5)+13;
(3)0+(-7); (4)(-4.7)+4.7.
例题
解:(1)(-4)+(-8)
=-(4+8)
=-12
(2)(-5)+13=+(13-5)=8
(3)0+(-7)=-7
(4)(-4.7)+3.9=-(4.7-3.9)=-0.8
通过有理数加法法则的学习,同学们,你们认为如何进行有理数加法运算呢?
方法总结:1.先判断类型(同号、异号等);
2.再确定和的符号;
3.最后进行绝对值的加减运算.
讨论
例2 已知│a│= 8,│b│= 2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
分析:先根据的a、b符号,分类讨论,再计算a+b的值
解:因为│a│= 8,│b│= 2,所以a= ±8,b= ±2.
(1) 因为a、b同号,所以a= 8,b= 2或a= -8,b= -2.
所以a+b= 8+2=10,或a+b=- 8+(-2)=-10.
(2) 因为a、b异号,所以a= 8,b=- 2或a= -8,b= 2.
所以a+b= 8+(-2)=6,或a+b=- 8+2=-6.
若|x-3|与|y+2|互为相反数,求x+y的值.
变式训练
解:由题意得|x-3|+|y+2|=0,又|x-3|≥0,|y+2|≥0,所以x-3= 0,y+2=0,所以x=3 ,y=-2.
所以x+y=3-2=1.
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
篮球共进( )球,失( )球,净胜球数为( ).
1
1
(+1)+(-1)=0
分析特征 强化理解 总结步骤
( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓
同号两数相加 取相同符号 通过绝对值化归
为算术数的加法
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓
异号两数相加 取绝对值较大 通过绝对值化归
的加数的符号 为算术数的减法
同号两数之和——这是名符其实的和,做加法。
异号两数之和——表面上叫“和”,其实是做减法。
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
小结:
【课后练习】
1.在学习“有理数的加法与减法运算”时,我们做过如下观察:“小亮操控遥控车模沿东西方向做定向行驶练习,规定初始位置为0,向东行驶为正,向西行驶为负.先向西行驶3m,在向东行驶lm,这时车模的位置表示什么数?”用算式表示以上过程和结果的是( )
A.(﹣3)﹣(+1)=﹣4 B.(﹣3)+(+1)=﹣2
C.(+3)+(﹣1)=+2 D.(+3)+(+1)=+4
2.计算(﹣20)+17的结果是( )
A.﹣3 B.3 C.﹣2017 D.2017
3.已知|a|=3,|b|=4,并且a>b,那么a+b的值为( )
A.+7 B.-7 C.±1 D.-7或-1
4.下列结论不正确的是( )
5.若两个非零有理数a,b,满足|a|=a,|b|=﹣b,a+b<0,则a,b的取值符合题意的是( )
A.a=2,b=﹣1 B.a=﹣2,b=1 C.a=1,b=﹣2 D.a=﹣1,b=﹣2
6.绝对值大于1小于4的整数的和是( )
A.0 B.5 C.﹣5 D.10
7.若a是最小的正整数,b是绝对值最小的数,c是相反数等于它本身的数,d是到原点的距离等于2的负数,e是最大的负整数,则a+b+c+d+e=_____.
8.如果|a|=4,|b|=7,且a<b,则a+b=______.
9.某人用400元购买了8套儿童服装,准备以一定价格出售.如果以每套儿童服装55元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,﹣3,+2,+1,﹣2,﹣1,0,﹣3(单位:元);
请通过计算说明:
(1)当他卖完这八套儿童服装后是盈利还是亏损?盈利(或亏损)了多少钱?
(2)每套儿童服装的平均售价是多少元?
10.已知|a|=8,|b|=2.
(1)当a,b同号时,求a+b的值;
(2)当a,b异号时,求a+b的值.
【课后练习】答案
1.B
2.A
3.D
4.D
5.C
6.A
7.﹣2 8.3或11
9.(1)当他卖完这八套儿童服装后是盈利了,盈利了36元;
(2)每套儿童服装的平均售价是54.5元.
10.(1)a+b=10或-10;(2)a+b=6或-6.
1.3.1有理数的加法
第一课时
【学习目标】
掌握有理数加法法则,能熟练进行有理数加法运算;
01
理解有理数加法意义
02
能利用有理数加法运算解决简单的实际问题。
03
【课前预习】
1.计算(﹣3)+5的结果等于( )
A.2 B.﹣2 C.8 D.﹣8
2.若|m|=3,|n|=5,且m-n>0,则m+n的值是( )
A.-2 B.-8或8 C.-8或-2 D.8或-2
3.有理数、在数轴上的位置如图所示,则的值( )
A.大于 B.小于 C.小于 D.大于
4.下面结论正确的有( )
①两个有理数相加,和一定大于每一个加数.
②一个正数与一个负数相加得正数.
③两个负数和的绝对值一定等于它们绝对值的和.
④两个正数相加,和为正数.
⑤两个负数相加,绝对值相减.
⑥正数加负数,其和一定等于0.
A.0个 B.1个 C.2个 D.3个
5.如果两个数的和是负数,那么这两个数( )
A.至少有一个为正数 B.同是正数 C.同是负数 D.至少有一个为负数
【课前预习】答案
1.A
2.C
3.A
4.C
5.D
【学习探究】
小青在一条东西向的跑道上,先走了5米,又走了3米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
因为小明最后的位置与行走方向有关!
规定: 向东为正 向西为负
1、 向东走5米,再向东走3米,两次一共向东走了多少米 ?
-1 0 1 2 3 4 5 6 7 8
(+5)+(+3)=8
5
3
东
西
2、向西走5米,再向西走3米,两次一共向西走了多少米 ?
-8 -7 -6 -5 -4 -3 -2 -1 0 1
- 3
- 5
(-5)+(-3)= - 8
东
西
3、 向东走5米,再向西走3米,两次一共向东走了多少米 ?
(+5)+(-3)=2
-1 0 1 2 3 4 5 6
5
-3
东
西
4、 向东走3米,再向西走5米,两 次一共向西走了多少米 ?
(+3)+(-5)= -2
-3 -2 -1 0 1 2 3 4
3
-5
东
西
5、 向东走5米,再向西走5米,两次一共 走了多少米?
5+(-5)=0
-1 0 1 2 3 4 5 6
- 5
5
东
西
6、 向西走5米,再向东走0米, 两次一共向西走了多少米?
(-5)+0= - 5
-5 -4 -3 -2 -1 0 1
-5
东
西
( - 7 ) + ( -6 ) = - 13
( - 8 ) + ( -6 ) = - 14
(+5) + ( + 15) = +20
(+9) + (+ 3) = + 12
从得数中你能发现它的符号有规律吗?
同号两数相加,取相同的符号,
并把绝对值相加.
规律
(2) (-3)+(-9)
= -(3+9)= -12
(3) (-13)+(-8)
= -(13+8)= -21
(1) 6 + 11
= +(6+11)= 17
(1) 6 + 11
(2)(-3)+(-9)
(3)(-13)+(-8)
解:
练习
(+ 5) + ( -3 ) = +2
(+3) + ( -5 ) = - 2
( +5) + ( - 9 ) = - 4
(- 11) + (+4 ) = - 7
从得数中你能发现它的符号有规律吗?
绝对值不相等的异号两数相加,
取绝对值较大的数的符号,
并用较大的绝对值减去较小的绝对值.
规律
(1) (-3)+ 9
(4)(-4.7)+ 3.9
= +(9-3)= 6
=-(4.7-3.9)= -0.8
(2) 10 + (-6)
(3) +(- )
= +(10-6) = 4
2
1
3
2
=-( - )= -
3
2
2
1
6
1
(1) (-3)+ 9
(2) 10 + (-6)
(3) +(- )
2
1
3
2
解:
(4)(-4.7)+ 3.9
练习
(+5)+(-5)=0
互为相反数的两个数相加得0
(-5)+0=-5
一个数同0相加,仍得这个数
规律
(1) -79+79
(2) 12+(-12)
= 0
= 0
(3) 5+0
(4) (-3)+0
= 5
= -3
练习
有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加
数的符号,并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得0.
3. —个数同0相加,仍得这个数.
例1 计算:
(1)(-4)+(-8);(2)(-5)+13;
(3)0+(-7); (4)(-4.7)+4.7.
例题
解:(1)(-4)+(-8)
=-(4+8)
=-12
(2)(-5)+13=+(13-5)=8
(3)0+(-7)=-7
(4)(-4.7)+3.9=-(4.7-3.9)=-0.8
通过有理数加法法则的学习,同学们,你们认为如何进行有理数加法运算呢?
方法总结:1.先判断类型(同号、异号等);
2.再确定和的符号;
3.最后进行绝对值的加减运算.
讨论
例2 已知│a│= 8,│b│= 2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
分析:先根据的a、b符号,分类讨论,再计算a+b的值
解:因为│a│= 8,│b│= 2,所以a= ±8,b= ±2.
(1) 因为a、b同号,所以a= 8,b= 2或a= -8,b= -2.
所以a+b= 8+2=10,或a+b=- 8+(-2)=-10.
(2) 因为a、b异号,所以a= 8,b=- 2或a= -8,b= 2.
所以a+b= 8+(-2)=6,或a+b=- 8+2=-6.
若|x-3|与|y+2|互为相反数,求x+y的值.
变式训练
解:由题意得|x-3|+|y+2|=0,又|x-3|≥0,|y+2|≥0,所以x-3= 0,y+2=0,所以x=3 ,y=-2.
所以x+y=3-2=1.
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
篮球共进( )球,失( )球,净胜球数为( ).
1
1
(+1)+(-1)=0
分析特征 强化理解 总结步骤
( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓
同号两数相加 取相同符号 通过绝对值化归
为算术数的加法
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓
异号两数相加 取绝对值较大 通过绝对值化归
的加数的符号 为算术数的减法
同号两数之和——这是名符其实的和,做加法。
异号两数之和——表面上叫“和”,其实是做减法。
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
小结:
【课后练习】
1.在学习“有理数的加法与减法运算”时,我们做过如下观察:“小亮操控遥控车模沿东西方向做定向行驶练习,规定初始位置为0,向东行驶为正,向西行驶为负.先向西行驶3m,在向东行驶lm,这时车模的位置表示什么数?”用算式表示以上过程和结果的是( )
A.(﹣3)﹣(+1)=﹣4 B.(﹣3)+(+1)=﹣2
C.(+3)+(﹣1)=+2 D.(+3)+(+1)=+4
2.计算(﹣20)+17的结果是( )
A.﹣3 B.3 C.﹣2017 D.2017
3.已知|a|=3,|b|=4,并且a>b,那么a+b的值为( )
A.+7 B.-7 C.±1 D.-7或-1
4.下列结论不正确的是( )
5.若两个非零有理数a,b,满足|a|=a,|b|=﹣b,a+b<0,则a,b的取值符合题意的是( )
A.a=2,b=﹣1 B.a=﹣2,b=1 C.a=1,b=﹣2 D.a=﹣1,b=﹣2
6.绝对值大于1小于4的整数的和是( )
A.0 B.5 C.﹣5 D.10
7.若a是最小的正整数,b是绝对值最小的数,c是相反数等于它本身的数,d是到原点的距离等于2的负数,e是最大的负整数,则a+b+c+d+e=_____.
8.如果|a|=4,|b|=7,且a<b,则a+b=______.
9.某人用400元购买了8套儿童服装,准备以一定价格出售.如果以每套儿童服装55元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,﹣3,+2,+1,﹣2,﹣1,0,﹣3(单位:元);
请通过计算说明:
(1)当他卖完这八套儿童服装后是盈利还是亏损?盈利(或亏损)了多少钱?
(2)每套儿童服装的平均售价是多少元?
10.已知|a|=8,|b|=2.
(1)当a,b同号时,求a+b的值;
(2)当a,b异号时,求a+b的值.
【课后练习】答案
1.B
2.A
3.D
4.D
5.C
6.A
7.﹣2 8.3或11
9.(1)当他卖完这八套儿童服装后是盈利了,盈利了36元;
(2)每套儿童服装的平均售价是54.5元.
10.(1)a+b=10或-10;(2)a+b=6或-6.
