人教版数学七年级上册1.3.1 有理数的加法课件(共26张)
文档属性
| 名称 | 人教版数学七年级上册1.3.1 有理数的加法课件(共26张) |  | |
| 格式 | pptx | ||
| 文件大小 | 825.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 09:39:15 | ||
图片预览




文档简介
有理数的加法
学习目标
经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.
能运用该法则准确进行有理数的加法运算.
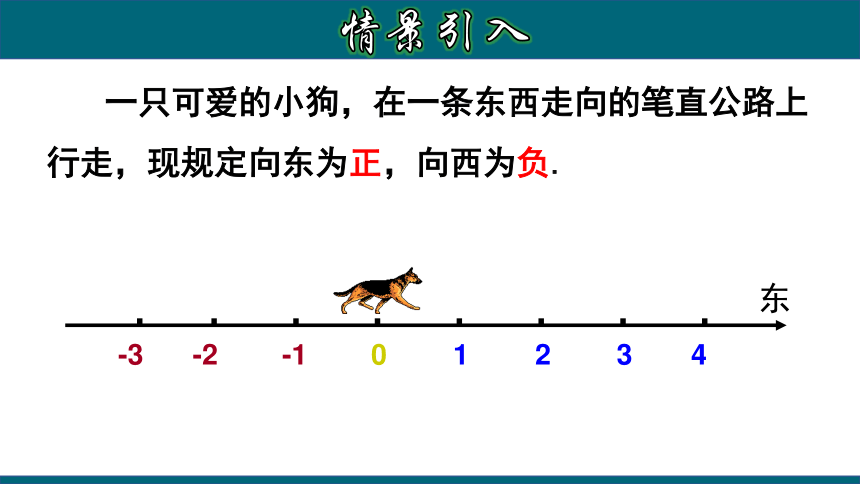
一只可爱的小狗,在一条东西走向的笔直公路上行走,现规定向东为正,向西为负.
0
1
2
3
4
-1
-2
-3
东
情景引入
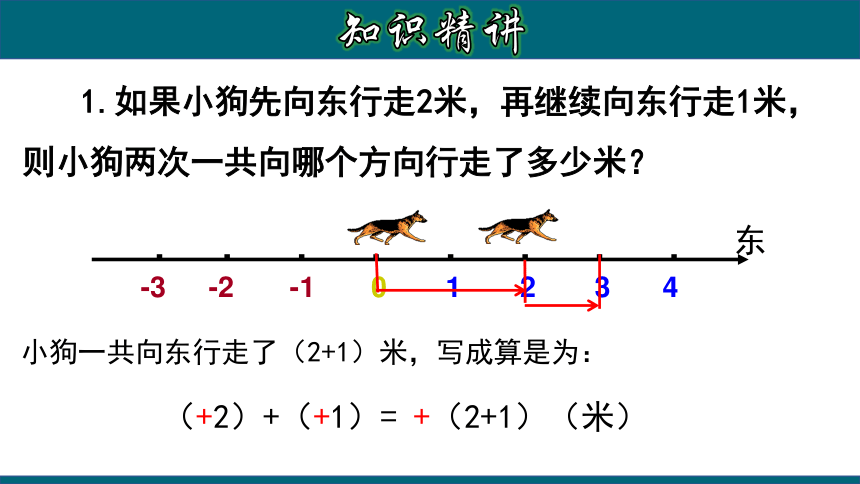
1.如果小狗先向东行走2米,再继续向东行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
东
小狗一共向东行走了(2+1)米,写成算是为:
(+2)+(+1)= +(2+1)(米)
知识精讲
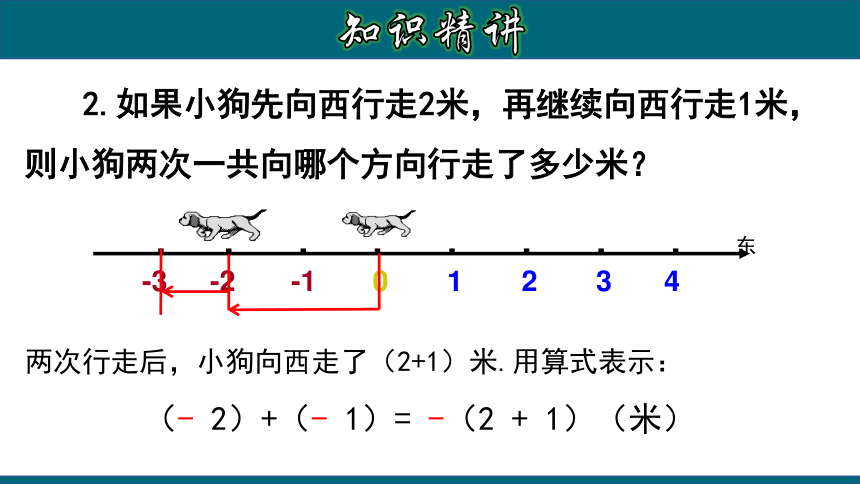
2.如果小狗先向西行走2米,再继续向西行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
东
两次行走后,小狗向西走了(2+1)米.用算式表示:
(- 2)+(- 1)= -(2 + 1)(米)
知识精讲
(+2)+(+1)= +(2+1)=+3
(-2)+(-1)= -(2+1)=-3
加数
加数
和
你从上面两个式子中发现了什么?
同号两数相加,取相同的符号,并把绝对值相加.
有理数加法法则一:
知识精讲
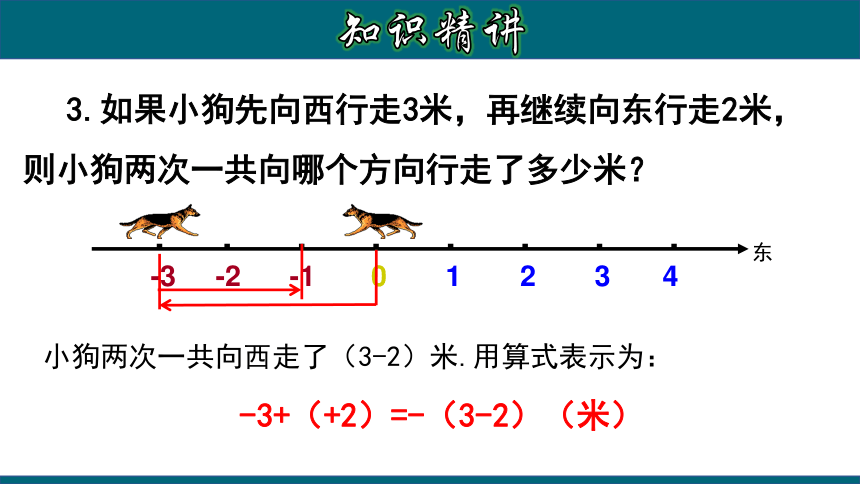
3.如果小狗先向西行走3米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-3 -2
东
小狗两次一共向西走了(3-2)米.用算式表示为:
-3+(+2)=-(3-2)(米)
知识精讲
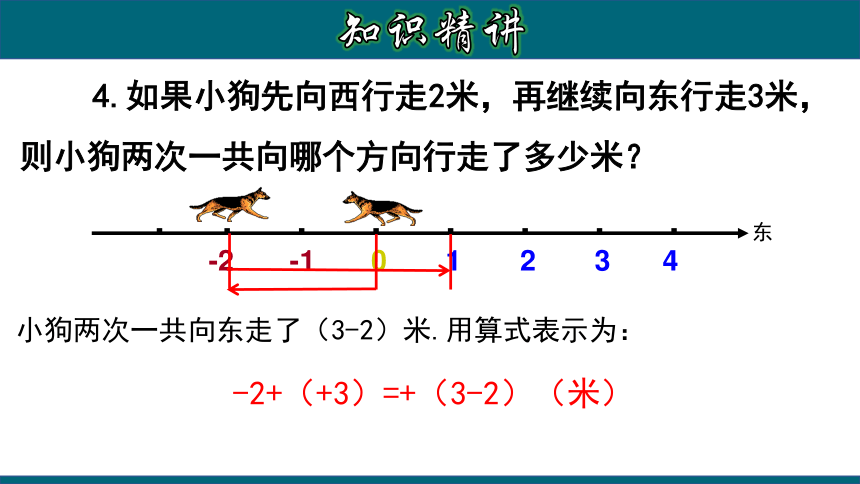
4.如果小狗先向西行走2米,再继续向东行走3米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
小狗两次一共向东走了(3-2)米.用算式表示为:
-2+(+3)=+(3-2)(米)
知识精讲
5.如果小狗先向西行走2米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
(-2)+(+2)= 0(米)
小狗一共行走了0米.写成算式为:
知识精讲
-2 + (+3) = +(3-2)
-3 + (+2)= -(3-2)
-2 + (+2)=0
加数
加数
和
加数异号
加数的绝对值不相等
你从上面三个式子中发现加数有什么特点?和又是怎么确定的?
知识精讲
加数的绝对值相等
有理数加法法则二:
异号两数相加,绝对值相等时和为0;
绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
知识精讲
6.如果小狗先向西行走3米,然后在原地休息,则小狗向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
小狗向西行走了3米.写成算式为:
(-3)+0= -3(米)
有理数加法法则三:
一个数同0相加,仍得这个数.
知识精讲
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值。互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
知识精讲
有理数的加法法则
例1 计算:
(1)(-4)+(-8);(2)(-5)+13;
(3)0+(-7); (4)(-4.7)+4.7.
解:(1)(-4)+(-8)=-(4+8)=-12
(2)(-5)+13=+(13-5)=8
(3)0+(-7)=-7
(4)(-4.7)+4.7=0
典例解析
有理数加法运算的基本解题思路:
1.先判断类型(同号、异号等);
2.再确定和的符号;
3.最后进行绝对值的加减运算.
知识精讲
例2 已知│a│= 8,│b│= 2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
分析:先根据的a、b符号,分类讨论,再计算a+b的值
解:因为│a│= 8,│b│= 2,所以a= ±8,b= ±2.
(1) 因为a、b同号,所以a= 8,b= 2或a= -8,b= -2.
所以a+b= 8+2=10,或a+b=- 8+(-2)=-10.
典例解析
例2 已知│a│= 8,│b│= 2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
分析:先根据的a、b符号,分类讨论,再计算a+b的值
解:因为│a│= 8,│b│= 2,所以a= ±8,b= ±2.
典例解析
(2) 因为a、b异号,所以a= 8,b=- 2或a= -8,b= 2.
所以a+b= 8+(-2)=6,或a+b=- 8+2=-6.
若|x-3|与|y+2|互为相反数,求x+y的值.
解:由题意得|x-3|+|y+2|=0,又|x-3|≥0,|y+2|≥0,
所以x-3= 0,y+2=0,
所以x=3 ,y=-2.
所以x+y=3-2=1.
变式练习
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
典例解析
解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为:
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为:
(+2)+(-4)=-(4-2)=-2
篮球共进1球,失1球,净胜球数为:
(+1)+(-1)=0
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
典例解析
1.两个有理数的和为零,则这两个有理数一定( )
A.都是零 B.至少有一个是零
C.一正一负 D.互为相反数
2.在1,-1,-2这三个数中,任意两数之和的最大值是( )
A.1 B.0 C.-1 D.3
D
B
达标检测
A. a+c<0 B. b+c<0 C. -b+a<0 D.-a+b+c<0
3.已知有理数a,b,c在数轴上的位置如图所示,则下列结论中错误的是( )
A.1 B.-5 C.-5或-1 D.5或1
4.若│x│= 3,│y│= 2,且x>y,则x+y的值为( )
C
D
达标检测
(1)(-0.6)+(-2.7); ? (2)3.7+(-8.4);?
(3)3.22+1.78; (4)7+(-3.3).?
5.计算
答案:(1)-3.3 (2)-4.7 (3)5 (4)3.7
达标检测
解:中午的气温为-25+11=-14℃,
夜间的气温为-14+(-13)=-27℃.
6.某城市一天早晨的气温是-25℃,中午上升了11℃,夜间又下降了13℃,那么这天中午、夜间的气温分别是多少?
达标检测
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值。互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
有理数的加法法则
小结梳理
学习目标
经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.
能运用该法则准确进行有理数的加法运算.
一只可爱的小狗,在一条东西走向的笔直公路上行走,现规定向东为正,向西为负.
0
1
2
3
4
-1
-2
-3
东
情景引入
1.如果小狗先向东行走2米,再继续向东行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
东
小狗一共向东行走了(2+1)米,写成算是为:
(+2)+(+1)= +(2+1)(米)
知识精讲
2.如果小狗先向西行走2米,再继续向西行走1米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
-3
东
两次行走后,小狗向西走了(2+1)米.用算式表示:
(- 2)+(- 1)= -(2 + 1)(米)
知识精讲
(+2)+(+1)= +(2+1)=+3
(-2)+(-1)= -(2+1)=-3
加数
加数
和
你从上面两个式子中发现了什么?
同号两数相加,取相同的符号,并把绝对值相加.
有理数加法法则一:
知识精讲
3.如果小狗先向西行走3米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-3 -2
东
小狗两次一共向西走了(3-2)米.用算式表示为:
-3+(+2)=-(3-2)(米)
知识精讲
4.如果小狗先向西行走2米,再继续向东行走3米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
小狗两次一共向东走了(3-2)米.用算式表示为:
-2+(+3)=+(3-2)(米)
知识精讲
5.如果小狗先向西行走2米,再继续向东行走2米,则小狗两次一共向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
(-2)+(+2)= 0(米)
小狗一共行走了0米.写成算式为:
知识精讲
-2 + (+3) = +(3-2)
-3 + (+2)= -(3-2)
-2 + (+2)=0
加数
加数
和
加数异号
加数的绝对值不相等
你从上面三个式子中发现加数有什么特点?和又是怎么确定的?
知识精讲
加数的绝对值相等
有理数加法法则二:
异号两数相加,绝对值相等时和为0;
绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
知识精讲
6.如果小狗先向西行走3米,然后在原地休息,则小狗向哪个方向行走了多少米?
0
1
2
3
4
-1
-2
东
小狗向西行走了3米.写成算式为:
(-3)+0= -3(米)
有理数加法法则三:
一个数同0相加,仍得这个数.
知识精讲
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值。互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
知识精讲
有理数的加法法则
例1 计算:
(1)(-4)+(-8);(2)(-5)+13;
(3)0+(-7); (4)(-4.7)+4.7.
解:(1)(-4)+(-8)=-(4+8)=-12
(2)(-5)+13=+(13-5)=8
(3)0+(-7)=-7
(4)(-4.7)+4.7=0
典例解析
有理数加法运算的基本解题思路:
1.先判断类型(同号、异号等);
2.再确定和的符号;
3.最后进行绝对值的加减运算.
知识精讲
例2 已知│a│= 8,│b│= 2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
分析:先根据的a、b符号,分类讨论,再计算a+b的值
解:因为│a│= 8,│b│= 2,所以a= ±8,b= ±2.
(1) 因为a、b同号,所以a= 8,b= 2或a= -8,b= -2.
所以a+b= 8+2=10,或a+b=- 8+(-2)=-10.
典例解析
例2 已知│a│= 8,│b│= 2;
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
分析:先根据的a、b符号,分类讨论,再计算a+b的值
解:因为│a│= 8,│b│= 2,所以a= ±8,b= ±2.
典例解析
(2) 因为a、b异号,所以a= 8,b=- 2或a= -8,b= 2.
所以a+b= 8+(-2)=6,或a+b=- 8+2=-6.
若|x-3|与|y+2|互为相反数,求x+y的值.
解:由题意得|x-3|+|y+2|=0,又|x-3|≥0,|y+2|≥0,
所以x-3= 0,y+2=0,
所以x=3 ,y=-2.
所以x+y=3-2=1.
变式练习
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
典例解析
解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为:
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为:
(+2)+(-4)=-(4-2)=-2
篮球共进1球,失1球,净胜球数为:
(+1)+(-1)=0
例3 足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
典例解析
1.两个有理数的和为零,则这两个有理数一定( )
A.都是零 B.至少有一个是零
C.一正一负 D.互为相反数
2.在1,-1,-2这三个数中,任意两数之和的最大值是( )
A.1 B.0 C.-1 D.3
D
B
达标检测
A. a+c<0 B. b+c<0 C. -b+a<0 D.-a+b+c<0
3.已知有理数a,b,c在数轴上的位置如图所示,则下列结论中错误的是( )
A.1 B.-5 C.-5或-1 D.5或1
4.若│x│= 3,│y│= 2,且x>y,则x+y的值为( )
C
D
达标检测
(1)(-0.6)+(-2.7); ? (2)3.7+(-8.4);?
(3)3.22+1.78; (4)7+(-3.3).?
5.计算
答案:(1)-3.3 (2)-4.7 (3)5 (4)3.7
达标检测
解:中午的气温为-25+11=-14℃,
夜间的气温为-14+(-13)=-27℃.
6.某城市一天早晨的气温是-25℃,中午上升了11℃,夜间又下降了13℃,那么这天中午、夜间的气温分别是多少?
达标检测
(1)同号两数相加,结果取相同符号,并把绝对值相加.
(2)异号两数相加,结果取绝对值较大的加数的符号,并将较大的绝对值减较小的绝对值。互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
有理数的加法法则
小结梳理
