人教版七年级数学上1.3.2有理数加减混合运算(第五课时)教学课件 (32张PPT)
文档属性
| 名称 | 人教版七年级数学上1.3.2有理数加减混合运算(第五课时)教学课件 (32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 11:07:14 | ||
图片预览











文档简介
有理数的加减混合运算拓展课
学生年级:七年级上册
学 科:数学
教材版本:人教版本
教学目标:
2、学会用扑克牌设计命题规则并命题
1、巩固有理数加减混合运算的常用技巧
3、培养数学创新思维,训练数学转化思想,
初步感知数学的“建模”思想。
1、有理数的加法法则
2、有理数的减法法则
3、有理数加减混合运算的常用技巧
温习:
有理数加减混合运算常用技巧:
1、同号相结合 2、相反数结合
3、同分母结合 4、凑整结合
复习回顾
(1)有理数的加法法则是什么?
(2)有理数的减法法则是怎样的?
有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
(3)互为相反数的两个数相加得零;
(4)一个数与零相加,仍得这个数;
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
即 a -b = a +(-b)
怎样进行有理数的加减混合运算呢?
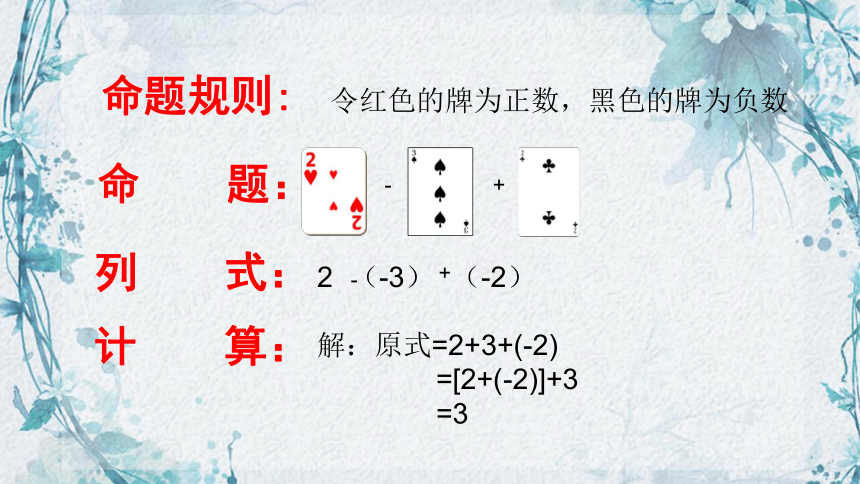
命题规则:
命 题:
列 式:
计 算:
-
+
-
+
解:原式=2+3+(-2)
=[2+(-2)]+3
=3
2
(-3)
(-2)
令红色的牌为正数,黑色的牌为负数
挑战成功要求:
1、至少设计出一个命题规则
2、命题时至少要能运用一个运算技巧
挑战第一关:一位数加减混合运算
挑战第二关:两位数加减混合运算
挑战成功要求:
至少设计出一个命题规则
挑战第三关:小数、分数、整数混合运算
(二)现定义一种新运算“*”,规定a*b=ab+a-b
如1*3=1×3+1-3,则(2*5)*6等于( )
(一)如果规定符号“?”的意义a?b=
则2?(-3)的值是( )
创新命题演练:
在代数里,一切加法与减法运算,都可以统一成加法运算。在一个和式里,通常有的加号可以省略,每个数的括号也可以省略。
如4.5+(-3.2)+1.1+(-1.4)可以写成省略括号的形式:
4.5 - 3.2 + 1.1 - 1.4(仍可看作和式)
读作 “正4.5、负3.2、正1.1、负1.4的和”
也可读作 “4.5减3.2加1.1减1.4”
加减法统一成加法
去括号法则
括号前是“+”号,去掉括号和它前面的“+”号,括号里面各项都不变;
括号前面是“-”号,去掉括号和它前面的“-”号,括号里的各项都变成它的相反数.
再看下面的例子:
(-8) - (-10) + (-6) - (+4)
=(-8)+(+10)+(-6)+(-4)(把减法运算统一成加法运算 )
=-8+10-6-4(省略括号和加号)
读作: 负8 正10 负6 负4 的和.
或: 负8 加10 减6 减4.
这就是省略加号的代数和.
1.有理数加减法统一成加法的意义
(1)有理数加减混合运算,可以通过有理数减法法则将减法转化为加法,统一成只有加法运算的和式,
如(?12)?(?8)?(?6)?(?5)
(2)在和式里,通常把各个加数的括号和它前面的加号省l略不写,写成省略加号的和的形式:
如 (?12)?(?8)?(?6)?(?5)
(3)和式的读法,一是按这个式子表示的意义,读作“
〃;
二是按运算的意义,读作“ 〃.
?(?12)?(?8)?(?6)?(?5)
??12?8?6?5
?12,?8,?6,?5的和
负12,减8,减6,加5
例题1
写成省略加号的和的形式, 并把它读出来。
把(+2/3)- 4/5 + 1/5- (-1/3) -1
思考
1.算式2-3-8+7可看作是哪几个有理数的代数和?
2.是否所有含有有理数加减混合运算的式子都能化成有理数的代数和?
3.有理数加法运算,满足哪几条运算律?
4.如何计算-3+5-9+3+10+2-1比较简便?
-3+5-9+3+10+2-1
=(-3+3)+〔(-1-9)+10〕+5+2
=0+0+5+2
=7
由于算式可理解为-3,5,-9,3,10,2,-1等七个数的和,因此应用加法结合律、交换律,这七个数可随意结合、交换进行运算,使运算简便。
加法运算律在加减混合运算中的应用
例1:计算
(1)-24+3.2-13+2.8-3
解: -24+3.2-13+2.8-3
=( -24-13-3 )+( 3.2+2.8)
= -40+6
= -34
解题小技巧:运用运算律将正负数分别相加。
例2:0-1/2- 2/3 -(-3/4)+(-5/6)
解: 0-1/2- 2/3 -(-3/4)+(-5/6)
=0-1/2-2/3+3/4-5/6
=(-1/2+3/4)+(-2/3-5/6)
=(-2/4+3/4)+(-4/6-5/6)
= 1/4 +(-3/2)
=1/4-6/4
=-5/4
解题小技巧:分母相同或有倍数关系的分数结合相加
例3(-0.5)-(-1/4)+(+2.75)-(+5.5)
解:(-0.5)-(-1/4)+(+2.75)-(+5.5)
=(-0.5)+(+0.25)+(+2.75)+(-5.5)
=-0.5+0.25+2.75-5.5
=(-0.5-5.5)+(0.25+2.75)
=-6+3
=-3
解题小技巧:在式子中若既有分数又有小数,把小数统一成分数或把分数统一成小数
例题2 计算
分析与解
(1)因原式表示省略加号的代数和,运用加法的交换律和结合律将加数适当交换位置,并作适当的结合后进行计算 :
-24+3.2-16-3.5+0.3
=(-24-16)+(3.2+0.3)-3.5
= -40+(3.5-3.5)
= -40+0 =-40
(交换位置后,整数,小数分别结合)
(交换位置,便于通分)
(减法转为加法,再运用交换律结合律)
练习(1)10-24-15+26-24+18-20
(2)(+0.5)-1/3+(-1/4)-(+1/6)
(1)解: 10-24-15+26-24+18-20
=(10+26+18)+(-24-15-24-20)
=54-83
=-29
(2)解:(+0.5)-1/3+(-1/4)-(+1/6)
=(+1/2)+(-1/3)+(-1/4)+(-1/6)
=1/2-1/3-1/4-1/6
=(1/2-1/4)+(-1/3-1/6)
=1/4-1/2
=-1/4
例题3
(1)(a+b)-(a-c)
(2)2(a-b)+(b+c)-IcI
(3)4(a-c)-(a+b+c)
(4)IaI+IbI+IcI-(a+b+c)
思维方式:
先化简,再把所给值代入后运用有理数加减混合运算法则及加法运算律进行计算。
小结:
打油诗一首《我心爱的扑克牌》
作业:发挥创造力,尽情玩扑克
训练创新思维游戏:
谢谢,再见!
学生年级:七年级上册
学 科:数学
教材版本:人教版本
教学目标:
2、学会用扑克牌设计命题规则并命题
1、巩固有理数加减混合运算的常用技巧
3、培养数学创新思维,训练数学转化思想,
初步感知数学的“建模”思想。
1、有理数的加法法则
2、有理数的减法法则
3、有理数加减混合运算的常用技巧
温习:
有理数加减混合运算常用技巧:
1、同号相结合 2、相反数结合
3、同分母结合 4、凑整结合
复习回顾
(1)有理数的加法法则是什么?
(2)有理数的减法法则是怎样的?
有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
(3)互为相反数的两个数相加得零;
(4)一个数与零相加,仍得这个数;
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
即 a -b = a +(-b)
怎样进行有理数的加减混合运算呢?
命题规则:
命 题:
列 式:
计 算:
-
+
-
+
解:原式=2+3+(-2)
=[2+(-2)]+3
=3
2
(-3)
(-2)
令红色的牌为正数,黑色的牌为负数
挑战成功要求:
1、至少设计出一个命题规则
2、命题时至少要能运用一个运算技巧
挑战第一关:一位数加减混合运算
挑战第二关:两位数加减混合运算
挑战成功要求:
至少设计出一个命题规则
挑战第三关:小数、分数、整数混合运算
(二)现定义一种新运算“*”,规定a*b=ab+a-b
如1*3=1×3+1-3,则(2*5)*6等于( )
(一)如果规定符号“?”的意义a?b=
则2?(-3)的值是( )
创新命题演练:
在代数里,一切加法与减法运算,都可以统一成加法运算。在一个和式里,通常有的加号可以省略,每个数的括号也可以省略。
如4.5+(-3.2)+1.1+(-1.4)可以写成省略括号的形式:
4.5 - 3.2 + 1.1 - 1.4(仍可看作和式)
读作 “正4.5、负3.2、正1.1、负1.4的和”
也可读作 “4.5减3.2加1.1减1.4”
加减法统一成加法
去括号法则
括号前是“+”号,去掉括号和它前面的“+”号,括号里面各项都不变;
括号前面是“-”号,去掉括号和它前面的“-”号,括号里的各项都变成它的相反数.
再看下面的例子:
(-8) - (-10) + (-6) - (+4)
=(-8)+(+10)+(-6)+(-4)(把减法运算统一成加法运算 )
=-8+10-6-4(省略括号和加号)
读作: 负8 正10 负6 负4 的和.
或: 负8 加10 减6 减4.
这就是省略加号的代数和.
1.有理数加减法统一成加法的意义
(1)有理数加减混合运算,可以通过有理数减法法则将减法转化为加法,统一成只有加法运算的和式,
如(?12)?(?8)?(?6)?(?5)
(2)在和式里,通常把各个加数的括号和它前面的加号省l略不写,写成省略加号的和的形式:
如 (?12)?(?8)?(?6)?(?5)
(3)和式的读法,一是按这个式子表示的意义,读作“
〃;
二是按运算的意义,读作“ 〃.
?(?12)?(?8)?(?6)?(?5)
??12?8?6?5
?12,?8,?6,?5的和
负12,减8,减6,加5
例题1
写成省略加号的和的形式, 并把它读出来。
把(+2/3)- 4/5 + 1/5- (-1/3) -1
思考
1.算式2-3-8+7可看作是哪几个有理数的代数和?
2.是否所有含有有理数加减混合运算的式子都能化成有理数的代数和?
3.有理数加法运算,满足哪几条运算律?
4.如何计算-3+5-9+3+10+2-1比较简便?
-3+5-9+3+10+2-1
=(-3+3)+〔(-1-9)+10〕+5+2
=0+0+5+2
=7
由于算式可理解为-3,5,-9,3,10,2,-1等七个数的和,因此应用加法结合律、交换律,这七个数可随意结合、交换进行运算,使运算简便。
加法运算律在加减混合运算中的应用
例1:计算
(1)-24+3.2-13+2.8-3
解: -24+3.2-13+2.8-3
=( -24-13-3 )+( 3.2+2.8)
= -40+6
= -34
解题小技巧:运用运算律将正负数分别相加。
例2:0-1/2- 2/3 -(-3/4)+(-5/6)
解: 0-1/2- 2/3 -(-3/4)+(-5/6)
=0-1/2-2/3+3/4-5/6
=(-1/2+3/4)+(-2/3-5/6)
=(-2/4+3/4)+(-4/6-5/6)
= 1/4 +(-3/2)
=1/4-6/4
=-5/4
解题小技巧:分母相同或有倍数关系的分数结合相加
例3(-0.5)-(-1/4)+(+2.75)-(+5.5)
解:(-0.5)-(-1/4)+(+2.75)-(+5.5)
=(-0.5)+(+0.25)+(+2.75)+(-5.5)
=-0.5+0.25+2.75-5.5
=(-0.5-5.5)+(0.25+2.75)
=-6+3
=-3
解题小技巧:在式子中若既有分数又有小数,把小数统一成分数或把分数统一成小数
例题2 计算
分析与解
(1)因原式表示省略加号的代数和,运用加法的交换律和结合律将加数适当交换位置,并作适当的结合后进行计算 :
-24+3.2-16-3.5+0.3
=(-24-16)+(3.2+0.3)-3.5
= -40+(3.5-3.5)
= -40+0 =-40
(交换位置后,整数,小数分别结合)
(交换位置,便于通分)
(减法转为加法,再运用交换律结合律)
练习(1)10-24-15+26-24+18-20
(2)(+0.5)-1/3+(-1/4)-(+1/6)
(1)解: 10-24-15+26-24+18-20
=(10+26+18)+(-24-15-24-20)
=54-83
=-29
(2)解:(+0.5)-1/3+(-1/4)-(+1/6)
=(+1/2)+(-1/3)+(-1/4)+(-1/6)
=1/2-1/3-1/4-1/6
=(1/2-1/4)+(-1/3-1/6)
=1/4-1/2
=-1/4
例题3
(1)(a+b)-(a-c)
(2)2(a-b)+(b+c)-IcI
(3)4(a-c)-(a+b+c)
(4)IaI+IbI+IcI-(a+b+c)
思维方式:
先化简,再把所给值代入后运用有理数加减混合运算法则及加法运算律进行计算。
小结:
打油诗一首《我心爱的扑克牌》
作业:发挥创造力,尽情玩扑克
训练创新思维游戏:
谢谢,再见!
