六年级上册数学课件-5.3 圆的整理和复习青岛版 (共55张PPT)
文档属性
| 名称 | 六年级上册数学课件-5.3 圆的整理和复习青岛版 (共55张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 13:31:35 | ||
图片预览






文档简介
(共55张PPT)
圆的整理和复习
青岛版六年级上册五单元
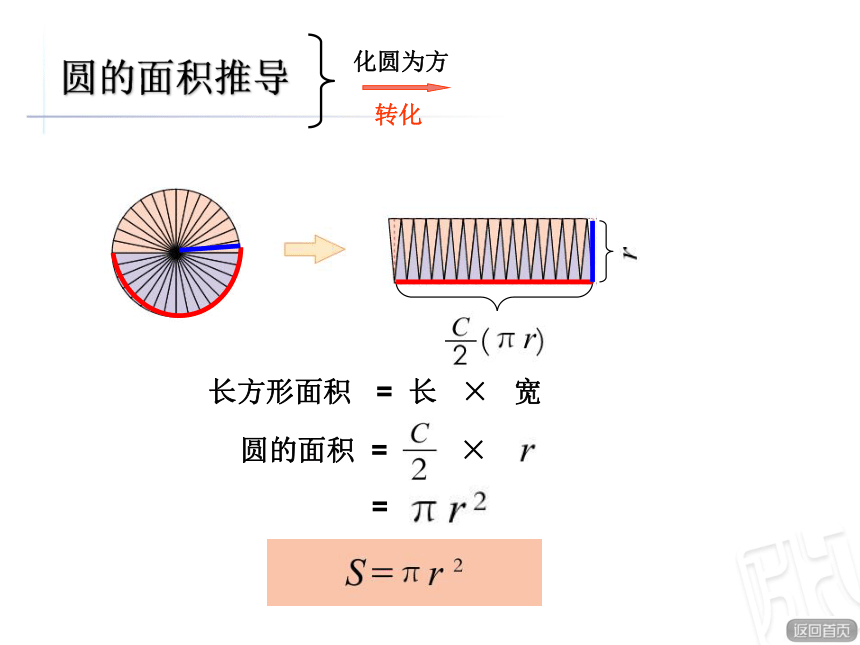
长方形面积
=
长
×
宽
圆的面积
=
×
=
圆的面积推导
化圆为方
转化
怎么能知道这顶太阳帽能遮住多少阳光?
生活中的圆
如果想在帽沿边上镶上彩条,需要多少彩条?
生活中的圆
如果把太阳帽的半径扩大2倍,哪些量会随着发生变化?会发生怎样的变化?
生活中的圆
如果想知道帽沿部分有多大,该怎么办?
生活中的圆
生活中的圆
思考:我们看到的太阳帽大部分都是圆形的,为什么不设计其它形状的太阳帽呢?(比如长方形或正方形)
8cm
4cm
生活中的圆
1、在这张长方形纸上剪下一个最大的圆,圆的面积是多少?
2、在这张长方形纸上剪下一个最大的半圆,半圆的面积是多少?
3、在这张长方形纸上最多能剪下多少个半径是1厘米的圆?
8cm
4cm
生活中的圆
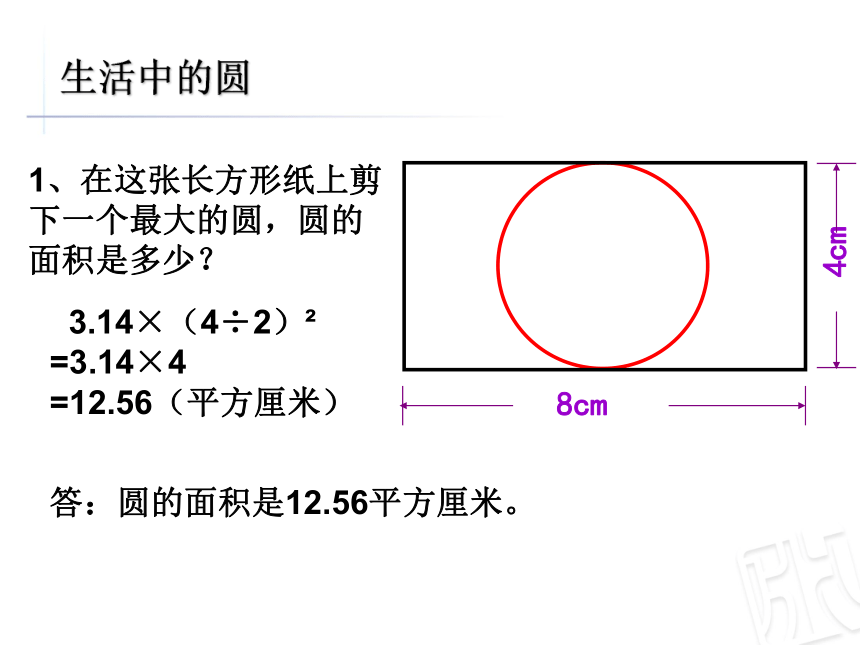
1、在这张长方形纸上剪下一个最大的圆,圆的面积是多少?
3.14×(4÷2)?
=3.14×4
=12.56(平方厘米)
答:圆的面积是12.56平方厘米。
8cm
4cm
生活中的圆
2、在这张长方形纸上剪下一个最大的半圆,半圆的面积是多少?
3.14×(8÷2)?÷2
=3.14×16÷2
=25.12(平方厘米)
答:半圆的面积是25.12平方厘米。
8cm
4cm
生活中的圆
3、在这张长方形纸上最多能剪下多少个半径是1厘米的圆?
1×2=2(厘米)
8÷2=4(个)
4÷2=2(个)
4×2=8(个)
答:最多能剪下8个圆。
8cm
4cm
拓展思维
利用12.56厘米长的棉线,将长方形纸围出我们学过的图形,怎样围面积最大?
一天,国王给狄多公主出了个难题:他给公主了一块牛皮,说:“你用这块牛皮圈土地,我就把圈到的土地给你。”一张牛皮能围多少地呢?聪明的狄多公主想了一个好办法。她用刀把牛皮割成很细的牛皮条,然后把牛皮条连成牛皮绳。用牛皮绳沿着海岸线,利用“天然的边界”圈出了一块很大的半圆形土地。国王佩服她的智慧,就把那块土地给了她。
狄多公主圈地
谢谢大家!
一、绕绳法
二、滚动法
圆的周长推导
化曲为直
转化
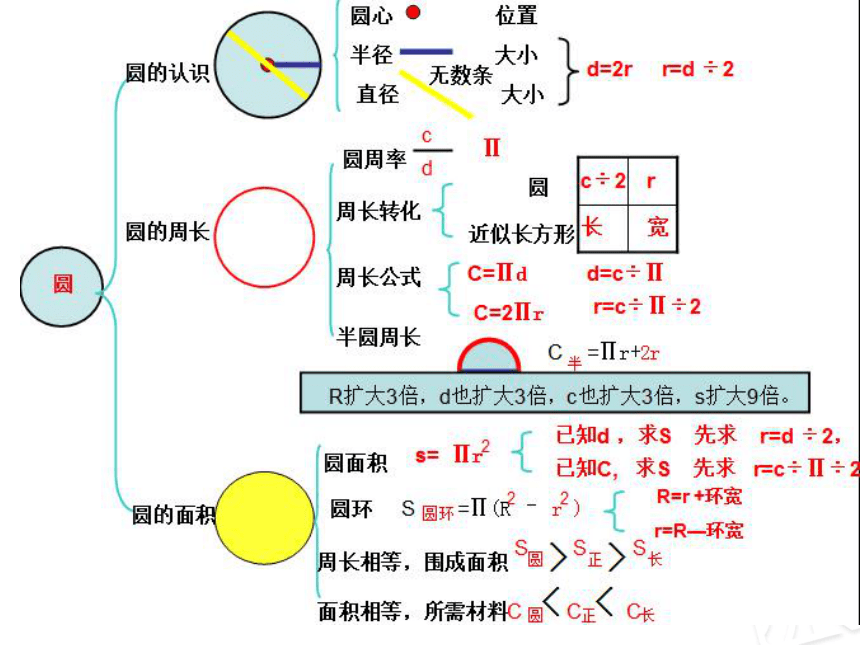
圆
圆的认识
圆的周长
圆的面积
位置
大小
直径
大小
无数条
圆心
半径
圆周率
面积转化
周长公式
半圆周长
圆
长方形
πr
长
宽
r
C=πd
C=2πr
圆面积
圆环
2
s=
πr
C
=∏r+2r
半
S
=π(R
–
r
)
圆环
2
2
d=2r
r=d
÷2
d
c
π
=
化曲为直
转化
化圆为方
转化
考考你
两只小蚂蚁打赌,它们以相同的速度沿着面积
都是12.56平方厘米的正方形和圆的周长爬行,
看哪个先爬完一周?
圆的周长推导
圆的周长推导
圆的周长推导
圆的周长推导
0
1
2
3
4
圆的周长推导
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
化曲为直
转化
圆的周长推导
d
c
π
=
C=πd
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
圆的面积推导
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
C
2
圆的面积推导
分的份数越多,拼成的图形越接近长方形。
r
C
2
圆的面积推导
r
C
2
=
πr
因为:
长方形面积
=
长
×
宽
所以:
圆
的
面
积
=
πr
×
r
=
πr
2
即:
S=πr
2
圆的面积推导
化圆为方
转化
(1)求周长:
3.14×2
=
6.28(米)
(2)求面积:
3.14×(2÷2)2
=
3.14(平方米)
(3)求能坐几人:
6.28÷0.5
≈
12(人)
答:它的周长是6.28米,面积是3.14平方米,大约能坐12人。
1.一个圆形餐桌的直径是2米,(1)在餐桌的周围镶上金属条,需要多少米?(2)如果在餐桌上铺上和桌面同样大小的水晶板,水晶板的面积是多少平方米?(3)如果一个人需要0.5m宽的位置就餐,这张餐桌大约能做多少人?
8米
(1)3.14×8
(2)3.14×8÷2
(3)3.14×8÷2+8
√
(求圆周长的一半)
(求圆的周长)
(求半圆的周长)
求草坪的周长
右图是一个一面靠墙,另一面用篱笆围成的半圆形养鸡场,这个半圆的直径为8米,篱笆长多少米?
8米
求篱笆的周长
(1)3.14×8
(2)3.14×8÷2
(3)3.14×8÷2+8
√
求下面图形的面积
4cm
3.14×4?÷2=25.12(平方厘米)
4cm
求下面图形的面积
3.14×4?÷2=25.12(平方厘米)
9厘米
3厘米
求下面图形的面积
9×3=27(平方厘米)
转化思想的应用
求阴影部分的周长(单位:m)
3.14×10+3.14×5
=3.14×(10+5)
=3.14×15
=47.1(米)
答:阴影部分的周长是47.1米。
数与代数
图形与几何
转化思想
异分母分数加减法
分数除法
除数是小
数的除法
平面图形
长方形
组合图形
立体图形
正整数
梯形
圆
三角形
平行四边形
体积
表面积
圆的整理和复习
青岛版六年级上册五单元
长方形面积
=
长
×
宽
圆的面积
=
×
=
圆的面积推导
化圆为方
转化
怎么能知道这顶太阳帽能遮住多少阳光?
生活中的圆
如果想在帽沿边上镶上彩条,需要多少彩条?
生活中的圆
如果把太阳帽的半径扩大2倍,哪些量会随着发生变化?会发生怎样的变化?
生活中的圆
如果想知道帽沿部分有多大,该怎么办?
生活中的圆
生活中的圆
思考:我们看到的太阳帽大部分都是圆形的,为什么不设计其它形状的太阳帽呢?(比如长方形或正方形)
8cm
4cm
生活中的圆
1、在这张长方形纸上剪下一个最大的圆,圆的面积是多少?
2、在这张长方形纸上剪下一个最大的半圆,半圆的面积是多少?
3、在这张长方形纸上最多能剪下多少个半径是1厘米的圆?
8cm
4cm
生活中的圆
1、在这张长方形纸上剪下一个最大的圆,圆的面积是多少?
3.14×(4÷2)?
=3.14×4
=12.56(平方厘米)
答:圆的面积是12.56平方厘米。
8cm
4cm
生活中的圆
2、在这张长方形纸上剪下一个最大的半圆,半圆的面积是多少?
3.14×(8÷2)?÷2
=3.14×16÷2
=25.12(平方厘米)
答:半圆的面积是25.12平方厘米。
8cm
4cm
生活中的圆
3、在这张长方形纸上最多能剪下多少个半径是1厘米的圆?
1×2=2(厘米)
8÷2=4(个)
4÷2=2(个)
4×2=8(个)
答:最多能剪下8个圆。
8cm
4cm
拓展思维
利用12.56厘米长的棉线,将长方形纸围出我们学过的图形,怎样围面积最大?
一天,国王给狄多公主出了个难题:他给公主了一块牛皮,说:“你用这块牛皮圈土地,我就把圈到的土地给你。”一张牛皮能围多少地呢?聪明的狄多公主想了一个好办法。她用刀把牛皮割成很细的牛皮条,然后把牛皮条连成牛皮绳。用牛皮绳沿着海岸线,利用“天然的边界”圈出了一块很大的半圆形土地。国王佩服她的智慧,就把那块土地给了她。
狄多公主圈地
谢谢大家!
一、绕绳法
二、滚动法
圆的周长推导
化曲为直
转化
圆
圆的认识
圆的周长
圆的面积
位置
大小
直径
大小
无数条
圆心
半径
圆周率
面积转化
周长公式
半圆周长
圆
长方形
πr
长
宽
r
C=πd
C=2πr
圆面积
圆环
2
s=
πr
C
=∏r+2r
半
S
=π(R
–
r
)
圆环
2
2
d=2r
r=d
÷2
d
c
π
=
化曲为直
转化
化圆为方
转化
考考你
两只小蚂蚁打赌,它们以相同的速度沿着面积
都是12.56平方厘米的正方形和圆的周长爬行,
看哪个先爬完一周?
圆的周长推导
圆的周长推导
圆的周长推导
圆的周长推导
0
1
2
3
4
圆的周长推导
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
圆的周长推导
0
1
2
3
4
化曲为直
转化
圆的周长推导
d
c
π
=
C=πd
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
圆的面积推导
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
C
2
圆的面积推导
分的份数越多,拼成的图形越接近长方形。
r
C
2
圆的面积推导
r
C
2
=
πr
因为:
长方形面积
=
长
×
宽
所以:
圆
的
面
积
=
πr
×
r
=
πr
2
即:
S=πr
2
圆的面积推导
化圆为方
转化
(1)求周长:
3.14×2
=
6.28(米)
(2)求面积:
3.14×(2÷2)2
=
3.14(平方米)
(3)求能坐几人:
6.28÷0.5
≈
12(人)
答:它的周长是6.28米,面积是3.14平方米,大约能坐12人。
1.一个圆形餐桌的直径是2米,(1)在餐桌的周围镶上金属条,需要多少米?(2)如果在餐桌上铺上和桌面同样大小的水晶板,水晶板的面积是多少平方米?(3)如果一个人需要0.5m宽的位置就餐,这张餐桌大约能做多少人?
8米
(1)3.14×8
(2)3.14×8÷2
(3)3.14×8÷2+8
√
(求圆周长的一半)
(求圆的周长)
(求半圆的周长)
求草坪的周长
右图是一个一面靠墙,另一面用篱笆围成的半圆形养鸡场,这个半圆的直径为8米,篱笆长多少米?
8米
求篱笆的周长
(1)3.14×8
(2)3.14×8÷2
(3)3.14×8÷2+8
√
求下面图形的面积
4cm
3.14×4?÷2=25.12(平方厘米)
4cm
求下面图形的面积
3.14×4?÷2=25.12(平方厘米)
9厘米
3厘米
求下面图形的面积
9×3=27(平方厘米)
转化思想的应用
求阴影部分的周长(单位:m)
3.14×10+3.14×5
=3.14×(10+5)
=3.14×15
=47.1(米)
答:阴影部分的周长是47.1米。
数与代数
图形与几何
转化思想
异分母分数加减法
分数除法
除数是小
数的除法
平面图形
长方形
组合图形
立体图形
正整数
梯形
圆
三角形
平行四边形
体积
表面积
